低压配电网电力线载波通信脉冲噪声过滤系统

李蕊， 丁宁， 史鹏博， 程诗尧， 李雪城

(国网北京电力科学研究院， 北京 100162)

0 引言

低压电力载波通信(Low-voltge Power Line Communication，LPLC)是一种通过电力线进行信号传递的通信方式，也是使用较早的PLC技术，被广泛应用在楼宇自动化系统、办公系统等自动化领域的网络中。但低压配电网中负载状况比较复杂，噪声种类多，其中脉冲噪声强度非常大，会导致传输信号的谐振与反射现象，进而造成信号衰减。

为改善通信质量，谭周文等[1]提出基于压缩感知与虚警概率相结合的脉冲噪声抑制方法。利用零子载波观测脉冲噪声投影，使用追踪降噪法估计脉冲噪声,结合门限获得噪声支撑集合，在该集合上通过最小二乘方法对信号进行重构，得到去噪后的通信信号。申敏等[2]提出基于迭代消除非线性失真的改进置零法来消除脉冲噪声。对接收到的时域信号进行脉冲检测与置零处理,从频域接收信号中去除重构的非线性失真，完成脉冲噪声抑制。

上述两种方法虽然能够获得较好的去噪效果，但是重构后的信号在幅度方面会有损失。为此，本文设计一种电力载波通信脉冲噪声过滤系统。

1 低压配电网电力载波通信脉冲噪声模型

低压配电网通信情况如图1所示。

图1 LPLC系统网络框图

低压配电网信道中存在多种噪声，其中最具代表性的是脉冲噪声，其又可以分为周期噪声[3]与随机噪声[4]。

(1) 周期脉冲噪声模型

周期噪声中包括单独脉冲与脉冲串，可看作是衰减的正弦波[5]。单独脉冲可通过指数规律衰减的正弦信号描述，如式(1)。

Nimp=Ae-t/τsin(2πft+φ)

(1)

式中，A为脉冲幅度，通过测量统计获得相应的概率分布情况；τ为时间常数。正弦波原始相位在0-2π之间随机生成[6]。脉冲频率也可称作伪频率f0，其累计分布与威布尔分布较为接近，分布函数表示为式(2)。

f(x)=abxb-1e-axb

(2)

根据真实频率分布规律能够将函数进行分段表示：当脉冲频率在600 kHz—5 MHz范围内时，参数取值为a=0.59、b=2.27；若频率高于5 MHz时，a=5×10-7、b=6.07。

脉冲串即为时间轴上的连续脉冲，是多个单独脉冲的累计，为式(3)。

(3)

式中，tarr表示脉冲生成时间。

(2) 随机脉冲噪声模型

表述噪声状态的n个状态Zi=(i,1,2,…,n)可被分解为A′(i-1,2,…,v)与B′(i=v+1,v+2,…,n)两部分，输出函数如式(4)。

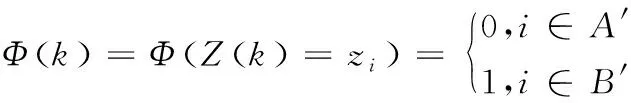
(4)

式中，A′与B′分别表示无脉冲状态与有脉冲状态。通过状态转移来实现汇总，构建A′与B′的独立转移状态矩阵。利用矩阵状态的改变来表示随机噪声模型。如果脉冲宽度高于设定值tw，其概率cpfw的表达式如式(5)。

(5)

若脉冲间隔高于固定值td时，概率cpfd能够表示为式(6)。

(6)

cpfw与cpfd由许多加权指数和组成，利用脉冲宽度与间隔获得矩阵元素值，再通过曲线进行拟合。

2 脉冲噪声过滤系统设计

2.1 系统硬件开发

去噪系统硬件包括传输模块、串口模块、储存模块和处理模块。硬件部分连接示意图如图2所示。

图2 硬件部分连接示意图

(1) 传输模块

低压配电网电力线载波通信需要长距离传输与性能稳定的传输通道，所以该模块利用RFTRI方式实现传输。本文选取的传输模块配备的天线标准是50欧姆，可使用配套的USB转换器、RS232/RS485转换器实现该模块与终端设备的连接，方便开发者测试有关通信。RFTRI模块的引脚定义如表1所示。

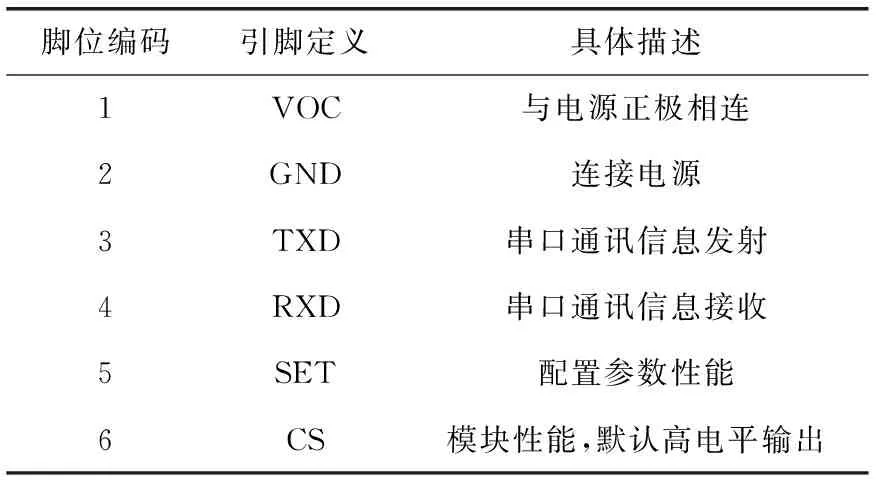
表1 RFTRI模块引脚定义表

(2)串口模块

串口又可以称为串行接口，也是一种通信接口。根据电气划分标准分为RS-232-C、RS-422、RS485。

RS-422、RS485与RS-232-C接口相比在传输距离与速度上更占优势。以飞凌公司配套提供的串口展示卡为例，将外部串口扩展为标准串口，方便与其它设备相连，如图3所示。

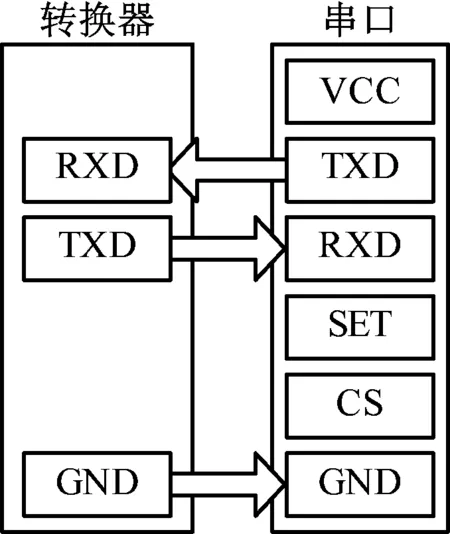
图3 串口模块连接示意图

(3) 储存模块

脉冲噪声过滤过程需接收与储存海量的数据，综合考虑数据量、设备功耗与开发成本等问题，在系统设计时可利用开发板的SD卡座外接SD卡进行储存。

(4)处理模块

处理模块选择的是S3C6410处理器，S3C6410集成一些硬件外设，例如I/O接口、电源接口、通道接口等，这些接口提高系统总体性能，减少投入成本。

2.2 系统软件设计

2.2.1 软件架构设立

噪声过滤系统中软件包括操作系统内核定制、设备驱动程序和应用程序。系统软件架构如图4所示。

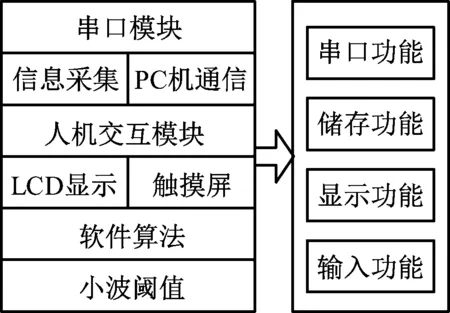
图4 噪声过滤系统软件结构示意图

内核定制部分是过滤系统的核心，负责控制系统流程、管理内存，决定系统的应用性能与稳定性。

2.2.2 软件算法研究

脉冲噪声过滤系统必须在某种去噪算法基础上进行，本文利用小波阈值去噪法来实现噪声过滤。

假设某存在噪声的一维信号模型表示为式(7)。

f′(t′)=s′(t′)+n′(t′)

(7)

式中，f′(t′)为带噪声信号；s′(t′)为有用信号；n′(t′)为噪声，可将其看作是一个噪声模量，满足N(0,σ2)分布的高斯白噪声。

小波阈值去噪的整体过程分为小波基选择、阈值函数构建、连续小波变换。

(1) 小波基选取

在小波变换过程中，小波基的选取会对信号的处理结果造成影响，进而改变去噪系统性能。在选取小波基时必须综合考虑消失矩、对称性与正则性三个性质。

消失矩：针对小波函数ψ(t′)∈L2(R)，如果符合式(8)。

(8)

则将ψ(t′)称为具备R阶的消失矩。根据小波函数零均值性质可得，任意小波函数最小存在零阶消失矩。

对称性：假设ψ(t′)∈L2(R)，若ψ(a+t′)=ψ(a-t′)，则表明ψ(t′)存在对称性；若ψ(a+t′)=-ψ(a-t′)，则ψ(t′)具备反对称性。

具有对称与反对称性质的小波函数能够构建紧支撑的小波基，更具有线性相位，这对于信号去噪非常有用。

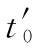
(9)

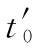
选取同时满足上述条件的小波基当作本文算法的小波基。

(2) 阈值函数构建

阈值函数能够表现出对小波系数进行处理所利用的方式，常用的算法是硬阈值与软阈值函数，但是这两种算法均存在一定局限性。为此，本文提出软、硬阈值折中函数为式(10)。

Wnew(j,k)=

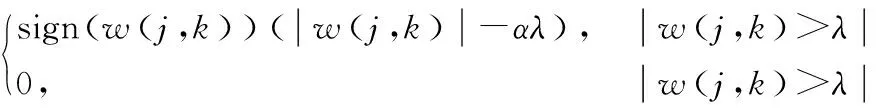
(10)

式中，w(j,k)表示带噪信号经过小波分解后的小波系数；λ表示选定阈值。

(3) 连续小波变换

对小波函数进行平移与伸缩变换可以获得小波序列，称其为子小波，表达式如式(11)。

(11)

式中，a为尺度因子，体现序列尺度；b为平移因子，反映小波函数在时间轴上的位置。ψa,b(t)通常是时域上以t=b为中心的带通函数，无论在时域还是频率上均存在局部化特征。

假设噪声信号f′(t′)的能量是有限的，即f′(t′)∈L2(R)，则连续小波变换式为式(12)。

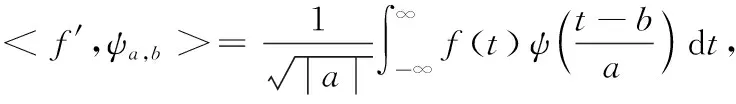
a≠0

(12)

式(12)表明小波变换将一元函数f′(t′)变换为时间-频率平面上的二元函数Wf′(a,b)，可将其当作是一个利用不同滤波器ψa,b(t)对信号f′(t′)进行过滤的过程。小波变换可以很好地体现信号每个瞬态分量存在的频率与发生时间，根据小波变换结果即可对初始信号进行重构，过滤掉信号中的噪声。

3 仿真实验数据分析与研究

本文对基于小波去噪的脉冲噪声过滤系统进行仿真实验，同时将仿真结果与文献[1]、文献[2]进行对比。实验中通信数据长度1 024 bit，子载波数量为98个，利用共轭对称方法对其调制，所以子载波总数量为196，零载波数量是850。脉冲噪声出现几率为0.011，噪声类型为高斯白噪声，噪声大小取决于信噪比，噪声和背景噪声的功率比为40 dB，信号和背景噪声的功率比为35 dB。初始信号与加入噪声后的信号波形图如图5所示。

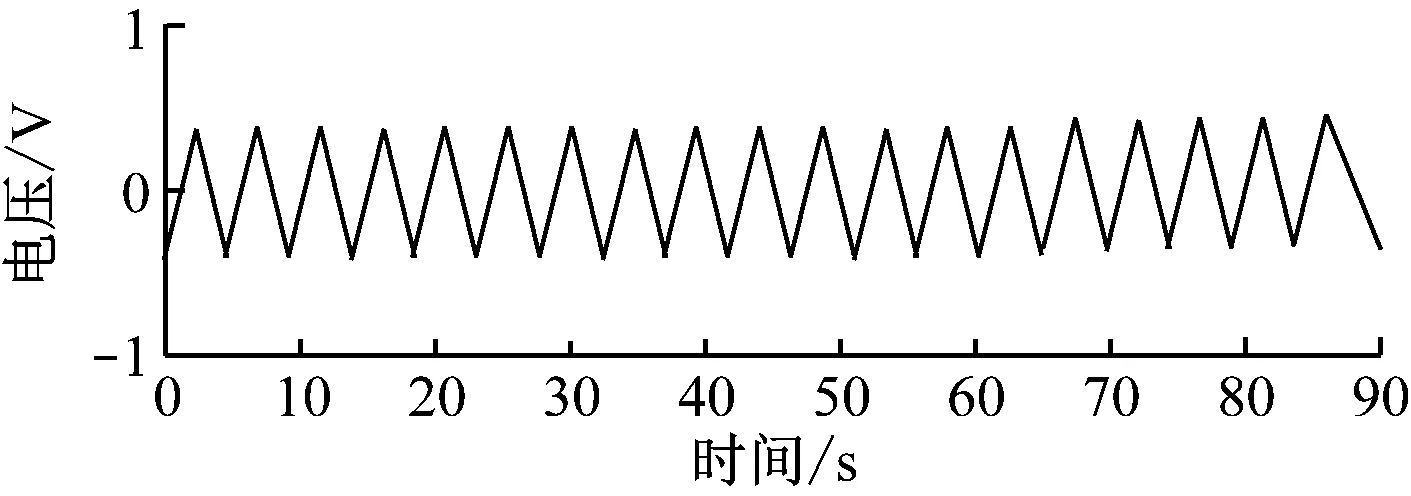
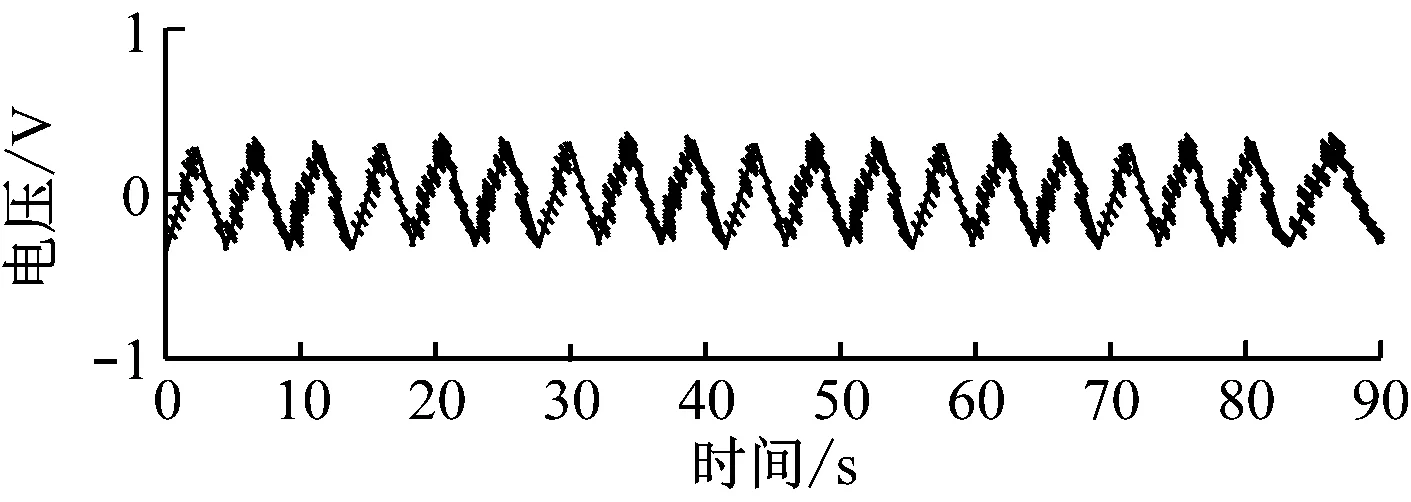
图5 初始信号与加噪信号波形图

分别使用三种不同方法对加噪后的信号进行去噪处理，去噪效果如图6所示。

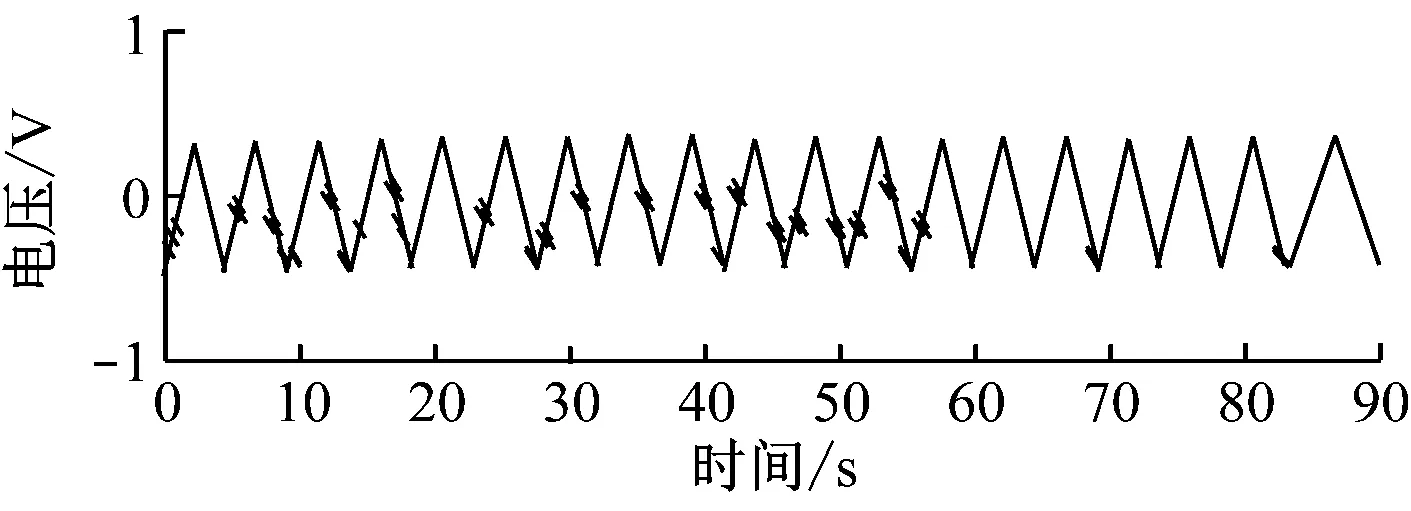
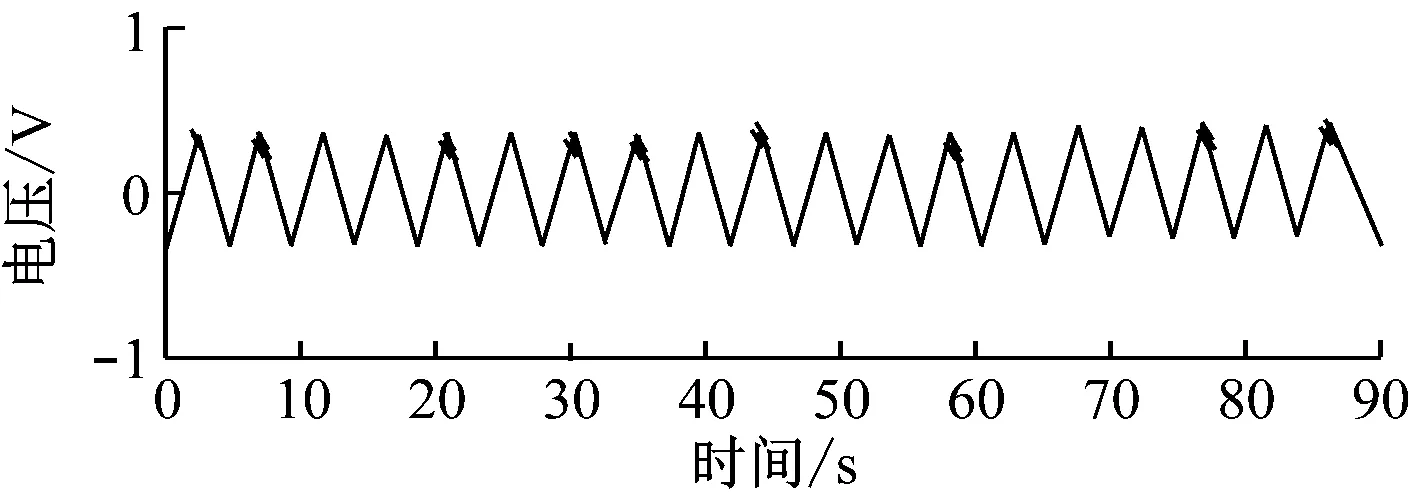
图6 不同方法噪声过滤效果对比图

由图6能够看出三种方法中，本文方法的过滤效果最好，与初始信号波形最接近;文献[1]方法对脉冲信号进行过滤，虽然能去除大部分噪声，但是前半部分信号噪声依旧较为明显，随着时间的推移，去噪效果有所改善；文献[2]方法去噪效果好于文献[1]，但是信号幅度方面会有损失，尤其在波峰位置，因此会导致传输性能下降，信号出现失真。此外，对比三种系统的误码率，结果如图7所示。

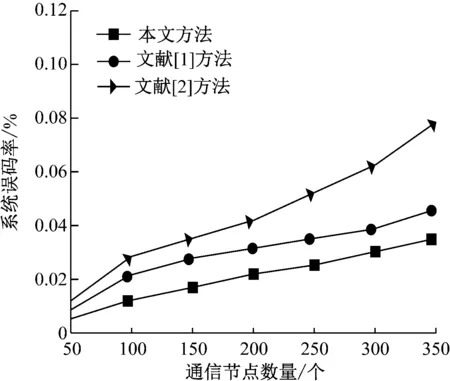
图7 系统误码率

由图7可知，随着节点的增加，通信范围不断扩大，其中噪声的干扰强度也随之提高。在此种环境下，本文方法噪声过滤系统展示出强大的性能，能够使传输误码率始终保持在较低状态。这正是由于小波阈值去噪方法可以在复杂的网络环境下对噪声进行准确过滤，才能有效提高传输性能，降低误码率。

4 总结

文章在ALTERA DE2开发板基础上设计一种噪声过滤系统，通过小波阈值法对小波进行变换，获得重构后的初始信号，实现小波过滤。实验证明，该方法具有较强的噪声过滤性能，能有效提高通信性能。

为此在下一步的研究中，可增加用户可控参数，使系统可以随机产生不同噪声数据，更好地验证系统性能。