一种SVM参数优化的模拟电路故障诊断仿真研究

周晚

(咸阳职业技术学院 机电学院， 陕西 西安 712000)

0 引言

快速发展完善的现代电子技术正在不断提高模拟电路的密集度与复杂度，这就需要保证模拟电路在运行过程中具有较高的可靠性，而电子设备的稳定运行离不开安全稳定的电路的支撑，不断扩大的模拟电路的应用范围，促使模拟电路的故障检测技术成为电路理论技术领域内的一项研究热点，尤其是在电路设计、设备生产、仪器维护中，模拟电路故障检测逐渐成为不可或缺的环节。

1 模拟电路故障诊断设计分析

1.1 设计需求分析

电子设备在发生电路故障时，如果不能及时发现解决将会对设备产生不同程度的损坏，进而对设备功能及设备使用寿命产生不利影响，为实现对模拟电路故障快速准确的诊断，学术界和工程界已开展了大量关于理论与方法方面的研究，相应的诊断理论与方法取得了一定的成果，目前人工智能方法(包括人工神经网络、支持向量机等)在模拟电路故障诊断方法中的融合正在不断深入，并取得了良好的效果。但仍有许多问题有待解决，如优化提取模拟电路故障特征的准确性及标准化水平有待提高，对模拟电路故障集的去噪能力较低，缺少对多分类组合策略科学合理的选择方法等，尤其是受到元件所具有的非线性特点的影响，相应的非线性模拟电路模型的复杂程度越来越高，传统故障特征提取方法存在的检测误差较大的问题日益突出，已经难以满足诊断需求[1]。

1.2 设计原理分析

模拟电路具有明显的非线性特点，对多数非线性系统较为精确的描述过程可通过Volterra级数实现，可有效满足对系统固有特性的反映需求，由于系统的输入输出不会对Volterra级数的时域核产生影响，使Volterra级数成为辨识模拟电路的一种实用工具。大量研究表明，在进行分类和预测时，采用基于统计学习理论的支持向量机(SVM)，惩罚因子和核函数参数等会对其准确率产生直接影响，通常需对SVM参数进行优化，现有的优化手段大多结合运用包括遗传算法、粒子群算法等在内的优化方法实现，并在提高分类效果的准确率方面取得了较好的效果。作为一种新型智能优化算法，入侵杂草算法(IWO)主要对杂草的入侵与繁殖进行仿生，各代杂草个体繁殖得到种子，标准的IWO算法中，这些种子在父代个体周围呈正态分布，此种寻优策略易导致算法陷入局部最优解，原因在于缺少对种群内部个体间信息的充分运用，后期种群易出现多样性变差[2]。本文采用SVM参数(经差分杂草算法优化)建立了一种最优故障诊断模型，结合运用Volterra级数完成故障的提取、分类和诊断。

2 支持向量机的优化

2.1 Volterra级数模型

在对非线性系统进行描述时，Volterra级数模型可有效满足描述需求，实现较精确的描述过程，模拟电路出现故障后，Volterra级数核会随之发生改变，Volterra级数模型可描述为式(1)。

(1)

对于一般的弱非线性系统，通常仅会使用到Volterra级数模型的前三阶，假设，测试信号的输入与对应输出分别由u(k)和y(k)表示，由L1、L2、L3表示前三阶的记忆长度分别，前三阶的时域核分别由h1(m1)、h2(m1，m2)、h3(m1，m2，m3)表示[3]，具体表达式如式(2)。

y(k)=y1(k)+y2(k)+y3(k)+e(k)

(2)

2.2 入侵杂草算法

仿生杂草入侵、繁殖、占领领地过程的入侵杂草算法的主要执行步骤如下[4]。

(1) 初始化，搜索空间的范围(维度)由D表示，可根据实际情况确定D和N的大小，随机产生的可行解个数由N表示，N即对应初始杂草种群。

(2) 繁殖，种群中全部个体中存在适应度的最低与最高值，确定各杂草个体所产生的种子数时，除了这两个适应度值外，还需考虑杂草个体的适应度值f，假设，在当代种群中，适应度的最低与最高值分别由fmin和fmax表示，初始设定的最大和最小种子数值由Smax、Smin表示，确定种子数量的计算表达式如式(3)。

(3)

(3) 空间分布，各杂草个体的种子在繁殖过程中的均值为父代个体所在位置，假设，各代标准差由σ表示，当前迭代次数由iter表示，正态分布标准差的初值和终值分别由σinit和σfinal表示，标准差的非线性调节指数由n表示，算法的最大迭代次数由itermax表示，具体关系计算表达式如式(4)。

(4)

(4) 竞争生存，在种群中杂草个体数量大于预设的Pmax的情况下，以具体适应度值为依据排序和淘汰处理杂草个体，使杂草数不超过Pmax。

(5) 循环操作步骤(2)—步骤(4)，直至得到最优解后输出。

2.3 差分进化算法

用于优化搜索基于群体智能的差分进化(DE)算法，更重视个体间的信息交流，其操作流程主要包括变异、交叉和选择，为有效实现向最优解的进化，以生成的中间个体(基于当代个体间的距离和方向信息得到)为依据作为优化策略，并根据对不同个体适应度值的计算与比较结果完成相应的保留与淘汰操作。DE算法的具体操作步骤如下[5]。

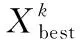
(5)

(6)

(7)

2.4 DE与IWO算法的融合

考虑到IWO算法缺少多样化的后期杂草种群的全局搜索能力降低，易陷入局部最优。为此本文在IWO算法融入了DE算法得到一种DEIWO算法，具体操作步骤为：先在杂草种群中每代个体完成繁殖与淘汰操作后，通过差分变异处理具有最优适应度值的个体实现中间个体的生成，再通过交叉处理原种群与中间种群完成试验个体的生成，最后对试验种群进行筛选(以适应度值为依据)。并采用Sphere和Rastrigin测试函数对比优化前后的算法的性能[6]，两种函数的表达式如式(8)、式(9)。

(8)

(9)

n=10时，Sphere和Rastrigin的适应度值变化曲线如图1所示。

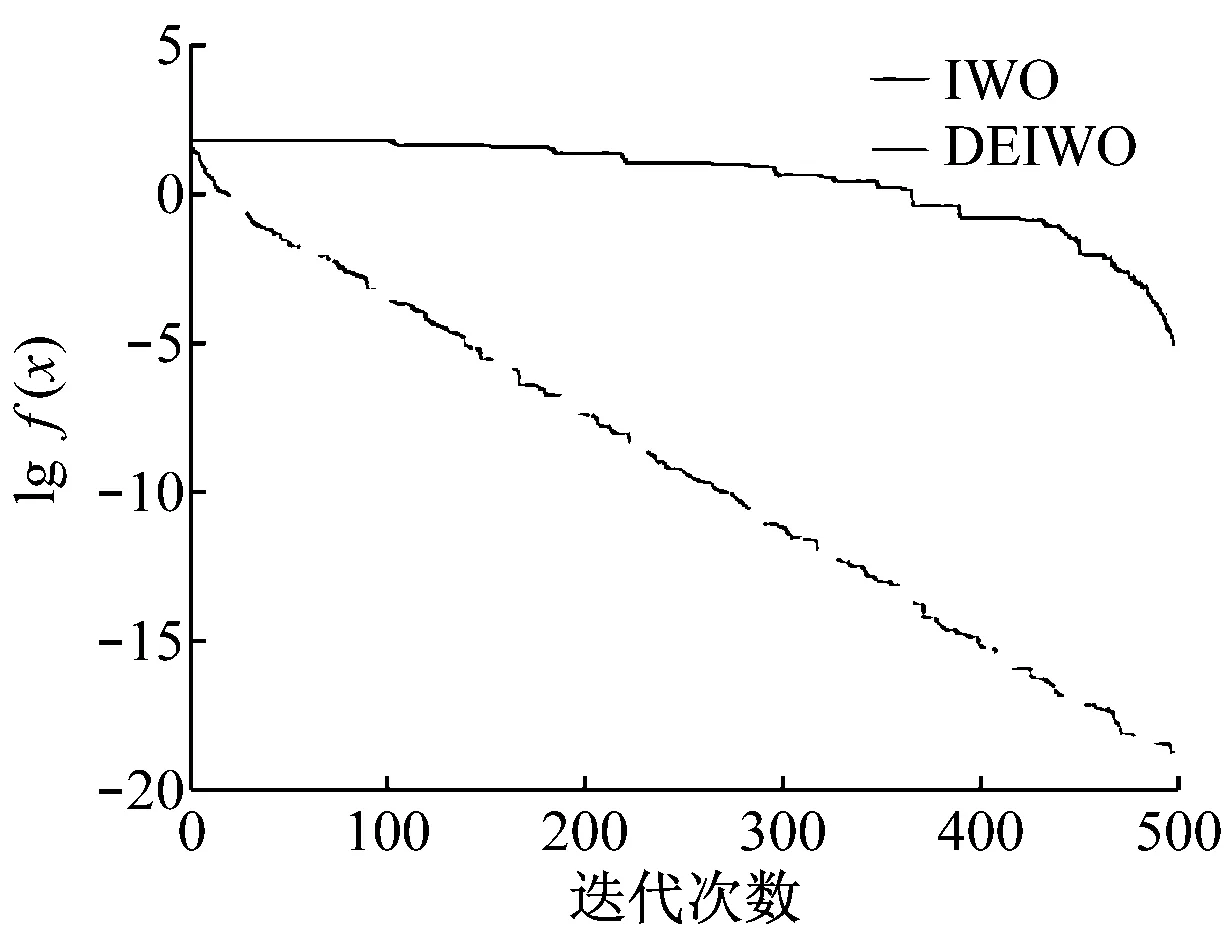
(a) Sphere函数收敛曲线

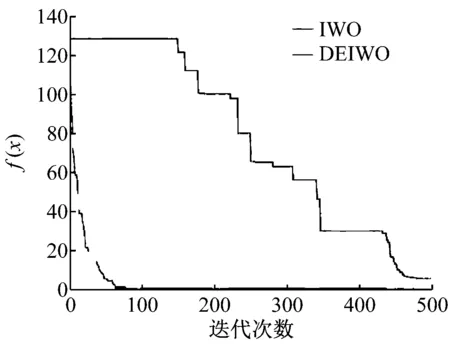
(b) Rastrigin函数收敛曲线图1 两种算法优化性能对比

Rastrigin函数下的DEIWO算法的收敛过程在较高维数下更加快速准确，有效解决了IWO算法易陷入局部最优的问题，可得到全局最优解。

3 故障诊断模型的建立

3.1 特征提取方法

针对已知故障电路，通过蒙特卡洛分析方法的使用，完成具体分析及正常元件参数(在容差范围内)的设置过程，对各类故障下的输入和输出信号即u(k)和y(k)进行测量，Volterra级数时域核序列的前三阶的求解过程使用递推最小二乘算法(RLS)完成，再对各阶序列的能量值进行计算[7],如式(10)。

(10)

在此基础上得出该电路的故障特征集Ot={E1，E2，E3}。

3.2 DEIWO-SVM算法流程

初始化处理DEIWO算法的参数值，产生K组SVM参数(由C和g表示)，通过SVM据此完成对训练集的学习，进而完成相应故障诊断模型的建立；接下来对各组参数对应的故障诊断准确率进行计算，具体通过使用V折交叉验证法完成，将计算结果作为杂草个体的适应度值；生成在父代杂草个体周围按N(0，σi)分布的杂草种子，根据繁殖进行情况不断更新σi值，并在解集中添加杂草种子，达到最大种群规模时从中选取Pmax个个体进行变异、交叉、选择操作，循环上述操作步骤进行优化，最终输出最优的C和g值，在此基础上建立用于故障诊断的诊断模型。基于DEIWO-SVM算法的故障诊断模型流程[7],如图2所示。

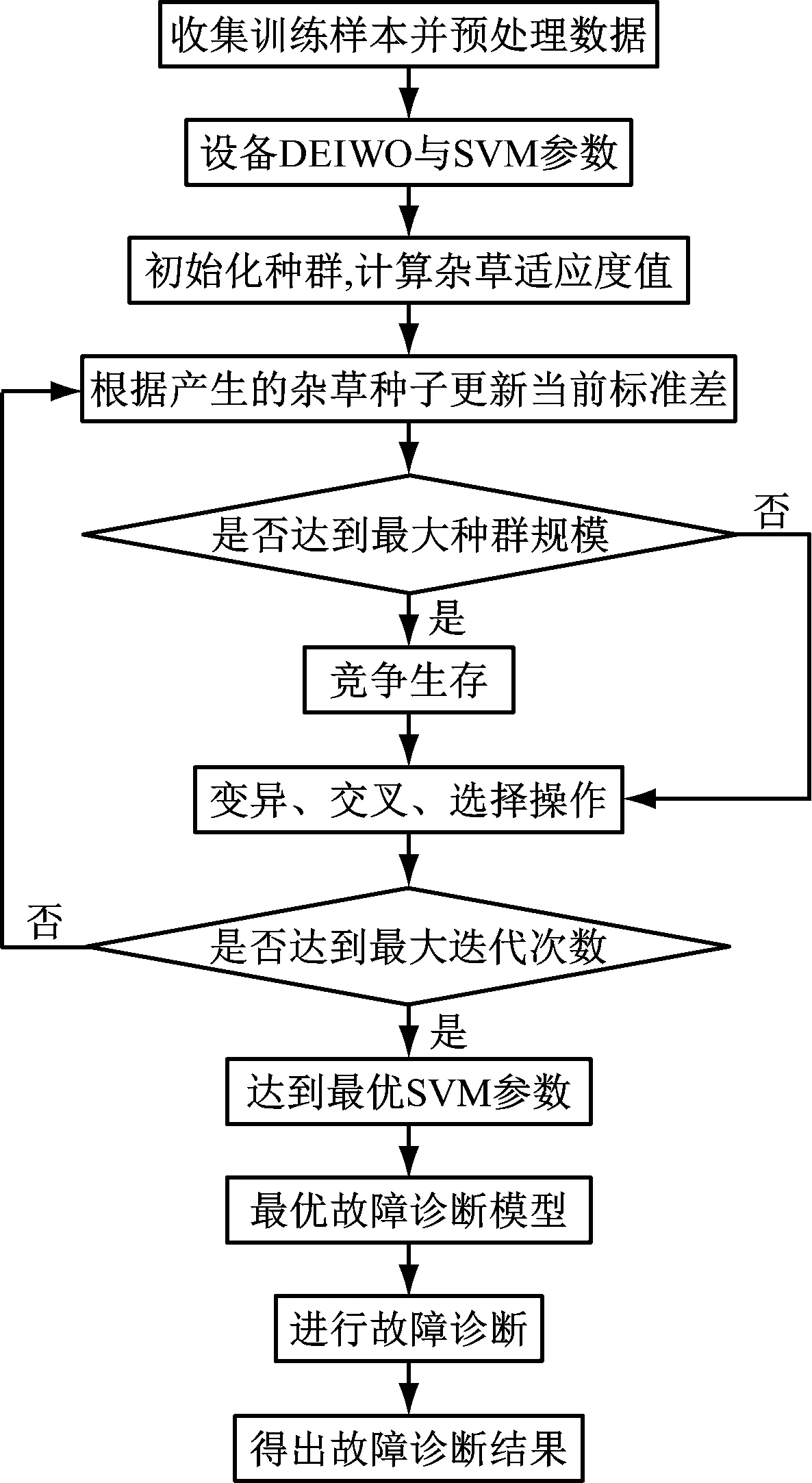
图2 故障诊断模型工作流程

4 仿真测试

为测试本文所设计的DEIWO-SVM算法的有效性，设计了相应的非线性模拟电路故障诊断测试仿真实验，仿真软件采用 Pspice9.0，实验对象采用了基于Volterra频域核辨识的对数放大器电路(以下简称为Volterra)中的，结合Volterra级数分析该软故障诊断方法，在输入端施加混合激励信号，对数放大器各电阻电容设置5%的容差，仅对部分元器件单一软故障进行考虑，电路的软故障状态对应元件标称值的1.1至1.3和0.7至0.9，以简化分析过程，设定的电路软故障集,如表1所示。

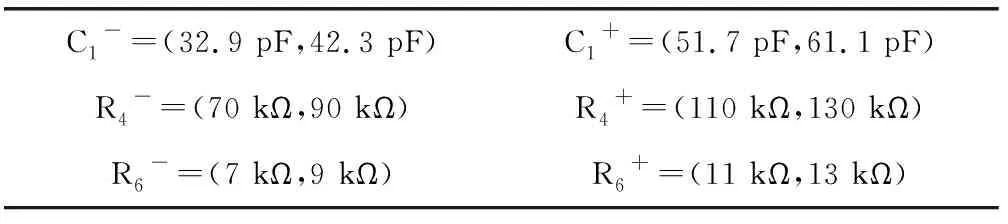
表1 电路软故障集

完成电路故障特征提取后，采用蒙特卡洛分析方法分析电路，对均取30组数据的各类故障采用本文方法完成分析计算过程，得到Volterra级数前三阶的能量值均值,如表2所示。

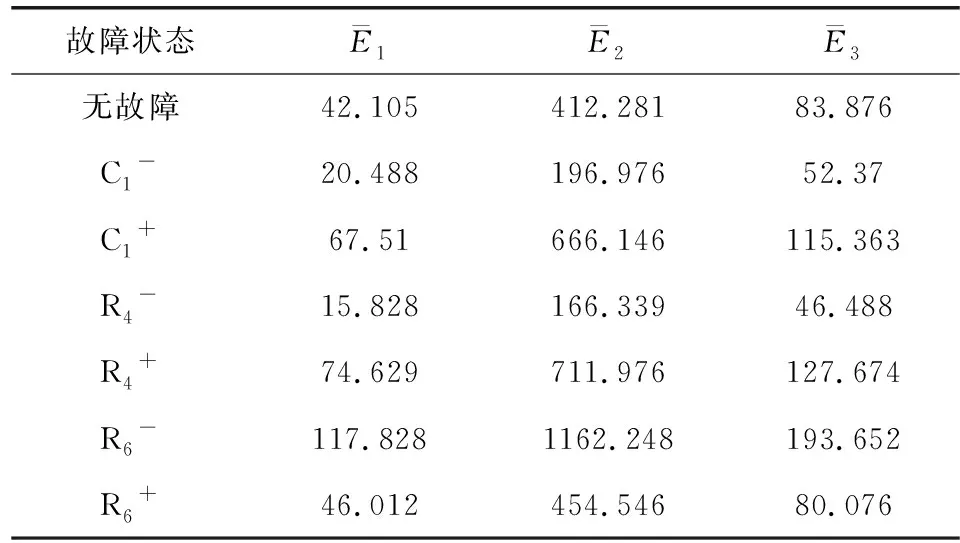
表2 Volterra级数各阶序列能量值均值

在各电路状态中，二阶序列能量值均值发生了明显的变化，一阶和三阶的变化不明显，说明电路同二阶非线性系统更接近，并且根据所提取出的故障特征可对各故障状态进行有效区分[8]。接下来在本文算法的分类器模型中输入提取到的故障特征，最终诊断结果如图3所示。

对比Volterra方法、经入侵杂草算法与粒子群算法优化的支持向量机方法(分别由IWO-SVM和PSO-SVM表示)及本文方法的故障诊断准确率，结果如表3所示。

相比其他三种方法，采用本文方法建立的故障诊断模型在总体与最低两项故障诊断率方面具有明显的优势，稍复杂于PSO-SVM算法的DEIWO-SVM算法有效提高了寻优精度和分类准确率，具有一定的实际应用价值。

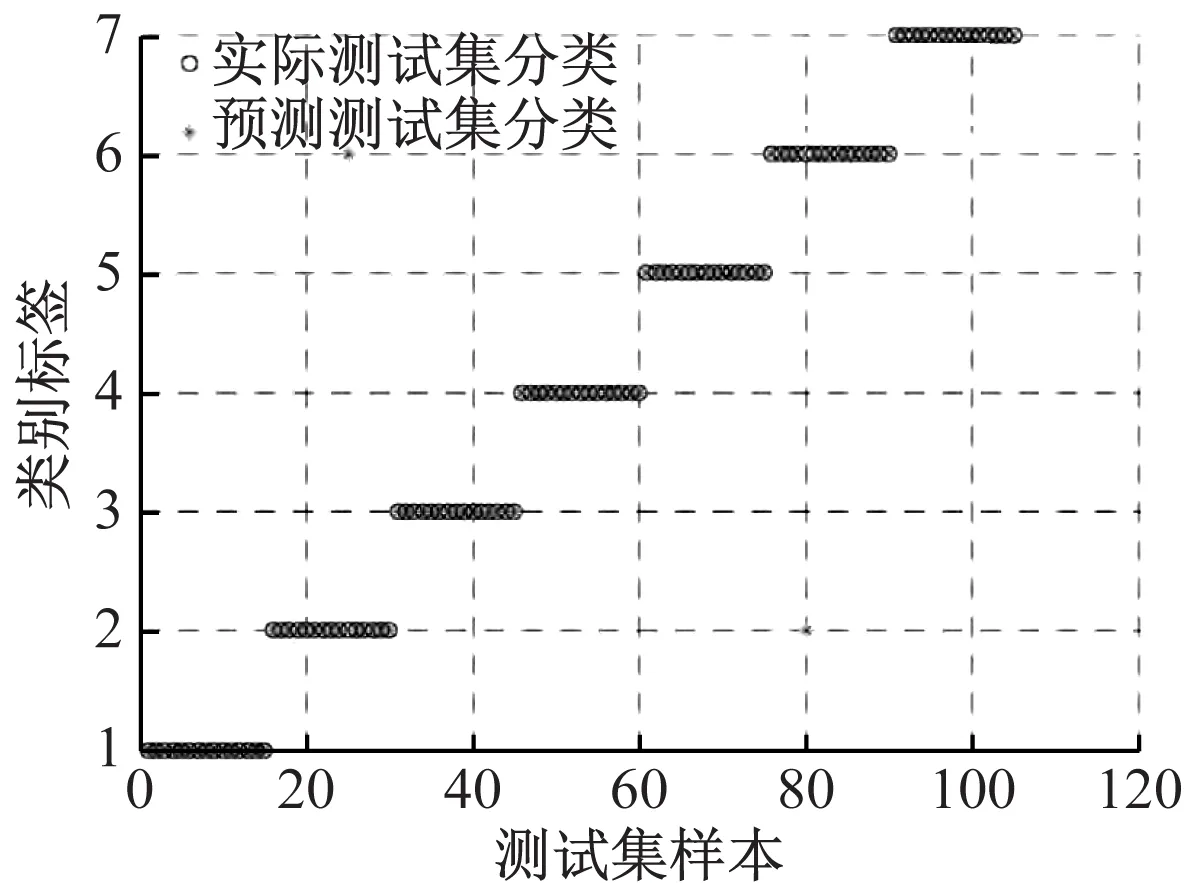
图3 本文算法的诊断结果

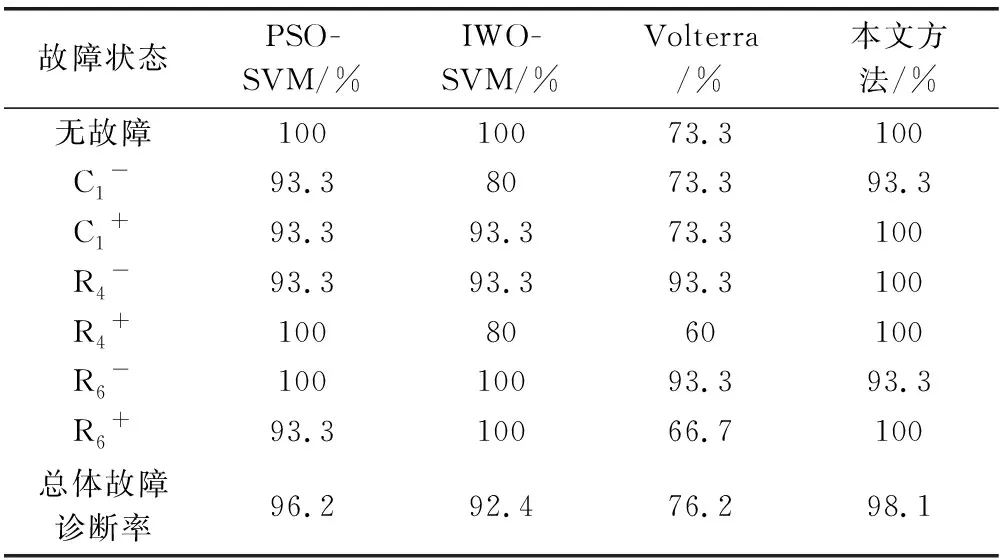
表3 故障诊断准确率的对比结果

5 总结

传统的模拟电路故障检测方法大多属于非线性模式，普遍存在软故障检测准确率不高及难以准确定位的不足，本文主要针对非线性模拟电路故障，通过进一步优化设计构建了一种诊断方法，SVM参数的优化使用DEIWO完成，并基于DEIWO-SVM建立了故障诊断模型，有效提高了故障特征提取与分类识别的效率和准确度，本文方法可使非线性模拟电路故障诊断的准确率得到有效提升。