基于有限元分析的建筑复合地基加固区沉降预测算法研究

王婷茹

(陕西铁路工程职业技术学院 高铁工程学院， 陕西 渭南 714000)

0 引言

地基是指建筑物下面支撑基础的土体或岩体。可以分为自然地基和复合地基两种[1]。在复合地基中，由于加固区与其他部位的密度不同，导致分散相颗粒在力场作用下的定向运动，引起沉降。通过对沉降量的预测，可估算出工后沉降量，计算当前固结度，确定预压时间，为整个建筑的施工进度安排提供参考。在进行现场地基沉降预测工作时，除了预测最终沉降外，有时还需要预测某一时刻软土的固结沉降。一般通常采用理论计算与现场实测数据分析相结合的方法，研究长短组合桩复合地基的沉降预测问题，并采用 ABAQUS有限元程序建立三维数值模型。在考虑分级填筑施工过程及长期荷载作用的基础上，对 CFG桩加固后路基填筑期和运营期的沉降进行数值模拟，分析 CFG桩筏复合地基沉降变形发展规律。当前关于不同时间点预测值和真实值之间误差的研究很少，一般认为，随着预测步数的增加，预测误差会逐渐增加，而定量分析则较少。因此，对软土固结沉降的预测应分阶段进行，并分析不同时间点的误差，对复合地基沉降量的预测和施工有一定的指导意义。

文献[2]用非线性有限元分析方法,建立加筋碎石桩群桩性能分析模型,计算分析不同因素对地基与桩顶沉降的影响。通过单桩与群桩沉降间的关系构建了考虑群桩效应的地基沉降比计算方法。文献[3]中地表沉降被认为是隧道开挖引起的不利影响。提出用(ICA)算法预测隧道开挖引起的最大地表沉降(MMS)。

传统预测方法在应用过程中存在着预测误差较大的问题，因此在传统预测方法的基础上，引入了有限元分析方法。有限元分析是一种基于变分原理求解数学物理问题的数值计算方法，是解决工程实际问题，数值计算的有力工具。该方法可应用于建筑复合地基加固区的沉降预测工作，以减少沉降预测误差，为工程施工提供更为精确的参考资料。

1 建筑复合地基加固区沉降预测算法设计

1.1 构建建筑复合地基加固区有限元模型

1.1.1 地基土体本构模型

复合桩基由钢筋混凝土板、碎石垫层、土工板和长桩组成。这种桩板结构变形协调，共同承受上部结构荷载。建筑物的复合地基土结构如图1所示。

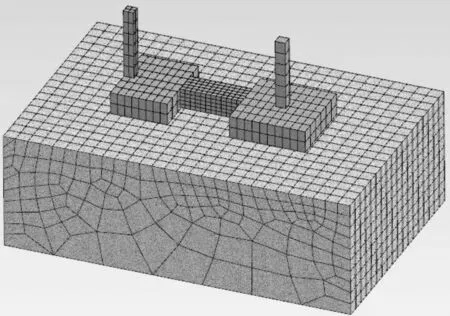
图1 复合地基土体本构模型示意图

图1中表示的本构模型的屈服条件主要包括6个屈服函数，其中部分屈服函数如式(1)。

(1)

同理可以得出其他两组屈服函数。式中c为复合地基土体的粘聚力;φ为土体的内摩擦角;而σ′为土体张拉强度[4]。

1.1.2 选取模型结构单元和土层材料参数

利用solid-45的三维结构实体单元，用contact-178单元点-点接触，可以将有限元模型简化为平面应变问题；以结构单元模型为基础，设置弹性模量、粘结力、摩擦角和密度等参数作为土层的材料参数，利用压缩模量计算弹性模量，并结合复合地基的实际地质条件对各参数进行量化选择[5]。

1.1.3 复合地基加固区固结有限元方程

在构建的有限元分析模型下，针对土体在加固区的固结问题，应用Biot固结理论[6]对加固区进行了具体分析。假定复合地基加固区土体还是匀质各向同性体，其渗透率随时间和空间变化不大，渗透系数为常数。由此可以得出复合地基加固区的土体平衡方程为式(2)。

(2)

式中,γ表示复合地基加固区土体的容量;而Fx、Fy和Fz表示的是x、y、z轴方向的总应力。把被分析土体结构分成若干空间节点的等参元，得出位移模式和坐标变换式[7]，并推导出加固区内各个单元结点力的表达式,如式(3)。

Fe=K0δ+Kβe

(3)

式中,参数K0和K分别为单元劲度矩阵和孔隙压力;δ为单元结点位移;βe为单元结点变量参数。对所有位移未知的结点建立平衡方程[8], 以矩阵表示为式(4)。

K0δ+Kβe=R

(4)

式中,R表示结点荷载向量。

1.1.4 设定模型初始和边界条件

用平衡方程反映了复合地基加固区内孔隙压力与外载荷的关系。但如在加荷前存在初始未完全消散的孔隙压力β0[9]的影响，此时存在式(5)。

(5)

式中,Rt表示在t-Δt 时刻以前各时刻发生的位移对应的应力所平衡了的荷载。初始荷载向量R0的表达式为式(6)。

R0=Ktβ0

(6)

式中，Kt为外载荷。模型边界条件可以分为位移边界条件和重力边界条件两部分，假设软土地基在自重作用下的沉降已完成，在沉降预测过程中外荷载仅考虑建筑重力。

1.1.5 复合地基的有限元作用机理

长短桩复合地基是由长短桩间距布置而成的。长短桩的作用机理是相互独立的，由它们形成的复合地基如图2所示。

图2 长短桩复合地基示意图

长桩又称主控桩[10]，主要用于控制沉降量。它承载了上部的大部分荷载，并通过桩体将其传递到深基础，以减少压缩层的变形，并与短桩一起，抑制了地基周围土体的上升。短桩又称辅助桩，其主要作用是提高地基下软土的承载力。长桩在进入深层承压层后对地基整体沉降起到了很好的控制作用，提高了地下室软弱层的承载力。

1.2 获取复合地基加固区沉降变形规律

复合地基加固区沉降可以大致的划分为3个阶段，分别为瞬时沉降、主固结沉降和次固结沉降。地基沉降计算的一般方程为式(7)。

S(t)=Sd(t)+Sc(t)+Ss(t)

(7)

式中,3个组成变量分别对应的是瞬时、主固结和次固结所产生的沉降。其中Sd(t)对应的是地基在受到外力作用下的瞬间所产生的沉降[11]。主固结和次固结沉降都是由于处理地基的过程中，加固区中的土体孔隙水流失，导致地基土体的体积逐渐减小，土体的密度增大后单位体积内土体的质量上升，最终导致软土地基的沉降增大。复合地基的沉降机理，除建筑物地基受力外，固结地基的压缩变形量和桩距的变化也是影响加固区沉降程度的影响因素。在不同因素的影响下，总结出复合地基加固区的沉降变形规律。

1.3 分析复合地基的应力-应变关系

有限元分析方法采用由有限个单元体组成的离散结构，取代原有的连续体结构，对应力变形进行分析。这种方法适用于处理非线性、非均匀、复杂边界条件下的复合地基应力-应变关系，适合于分析结构有限元模型[12]。其表达式为式(8)。

{σ}=[D]{ε}

(8)

其中,{σ}为应力状态;{ε}为应变状态;[D]为弹性矩阵。综合考虑加固区沉降变形规律及影响因素，从外荷载和加固区压缩两个方面对其应力-应变关系进行了量化分析。在有限元模型边界条件的约束下，可以用Fp表示复合地基内桩体的总应力，由桩体应力可以获得桩体应变,通过积分得到桩体的总压缩量为式(9)。

(9)

式中,pp为桩间土表面处的荷载集度;L为桩长;Ep为桩体的弹性模量。通过数据模拟和代入可以得出应力-应变之间的关系,如图3所示。

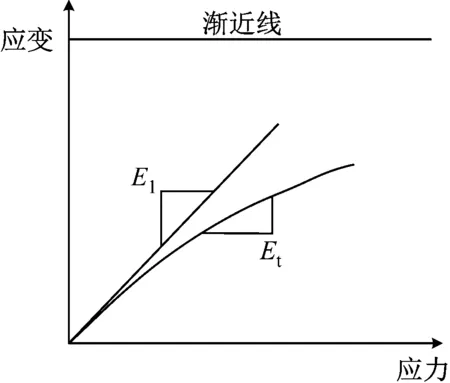
图3 应力-应变关系曲线图

1.4 计算建筑复合地基加固区应力

建筑用复合地基加固区的应力可分为初始静应力、土体固结时序荷载和附加应力三部分。初始静应力是指地基在土层自重和路堤荷载共同作用下所产生的应力。初步的静力应力场的确定[13]是用来计算静球面应力、静偏应力和静力强度的大小，分别计算变形模量和泊松比两个模型参数，得出初始应力值的计算结果。考虑施工过程荷载是随时间逐级施加的，加荷之间也可能存在间隙，因而实际计算是按一个Δt时间间隔进行的。将载荷分成阶段，分别施加于不同的时刻，如此反复可计算各级荷载。在固结有限元计算过程中第一个Δt取值有式(10)。

(10)

其中,B为体积模量;G为剪切模量;γw为复合地基加固区土体的重量。在复合地基上部，由建筑物的重力、人和交通的运动等引起的附加应力[14-15]，复合地基在垂直集中力作用下的受力分析示意图,如图4所示。

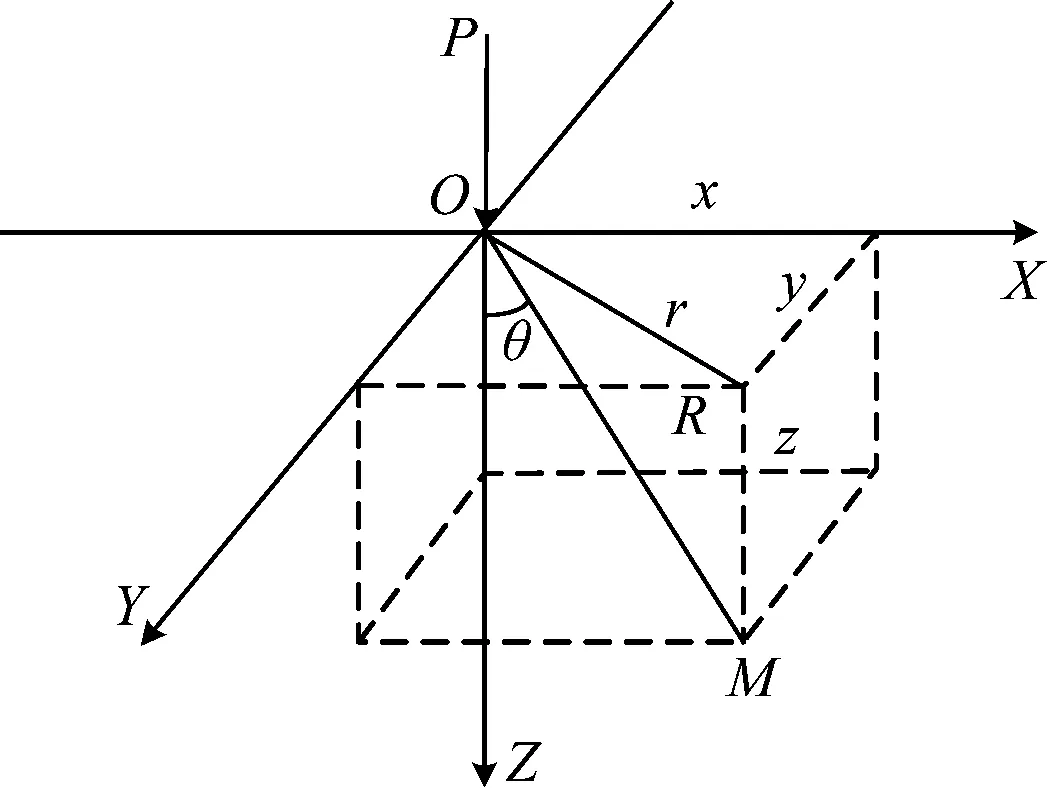
图4 受竖向集中力作用示意图

由此可以计算出复合地基上任意点的竖向应力值,如式(11)。

(11)

式中,P为总压力值;α为应力系数。

1.5 实现建筑复合地基加固区沉降预测

基于所建立的有限元模型，假定建筑物加固复合地基的平均沉降速率为双曲线形式，则自然条件下，任意时刻t的沉降可由式(7)计算得出。在综合考虑外部应力的情况下，结合应力与应变之间的关系，计算残余沉降量ΔS。ΔS和S(t)的和就是建筑负荷地基加固区的沉降量预测结果。

2 性能测试实验分析

为了测试设计的基于有限元分析的建筑复合地基加固区沉降预测算法的预测功能，设计性能测试实验。在实验中分别设置传统的沉降预测方法和文献[12]中提出的基于变权重组合预测模型的路基沉降预测方法作为实验的两个对比方法，通过对比体现出设计预测方法的运行优势。

2.1 工程概况

实验以某大型购物中心建筑为研究对象，起止桩号为K74+400—K155+724.819，地理坐标位于东经118°10′—118°50′，北纬34°15′—35′。整座建筑物的总建筑面积为2 421.46 m2，其施工范围内钻孔控制深度为第四纪洪积层，其中以粉土、粉质土、粉砂土、粉细砂组成的冲积层为主。

2.2 设置建筑复合地基加固区材料参数

性能测试实验分析中计算时间取100天，路基填料材料采用Mohr-Coulomb模型计算，路基填筑时间取80天，路基按不透水材料考虑。地基土材料采用Hardening soil模型设置。建筑复合路基地基材料参数如表1所示。

表1 建筑复合路基地基材料设置表

2.3 描述实验过程

由于设计的沉降预测算法应用了有限元分析技术，因此需在实验环境中安装 ANSYS软件。该软件的运行界面如图5所示。

图5 ANSYS 软件运行界面

分别将3种沉降预测方法代入到主测计算机中，并将建筑复合地基工程的相关项目参数导入其中，在预测算法的运行过程中，设计的预测算法可以调用有限元分析软件中的数据，但另两个对比软件不能调用。由于此次实验的测试目的是测试预测算法的功能运用结果，因此设置预测误差作为测试量化对比对象，设置两个加固区的实际地基的沉降量，并将3种方法的预测结果与设置标准值进行比对，便可以得出有关于预测误差的对比结果。实际复合地基沉降量的设置情况如图6所示。

图6 实际负荷地基沉降量设置曲线

2.4 实验结果对比分析

经过数据的统计与计算得出测试结果,如表2所示。

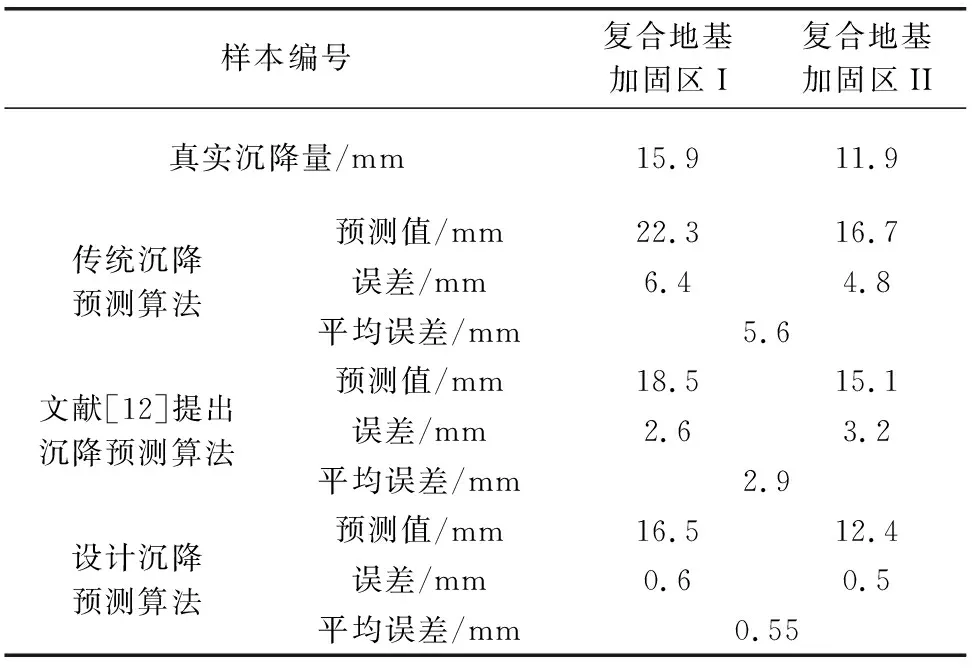
表2 预测误差测试对比结果

从表2中可以看出，经过与两个对比方法的比对可以看出，设计预测算法的预测误差得到了有效控制。

为验证所得预测误差结果的实际有效性，进行多次重复性误差实验。重复性误差实验对比结果,如图7所示。

图7 重复性误差实验对比结果

由图7可知，经过多次重复实验，本文设计的沉降预测算法的预测误差平均值保持在0.5 mm左右，文献[12]提出沉降预测算法的预测误差平均值保持在3 mm左右，传统沉降预测算法的预测误差平均值保持在6 mm左右，有效验证了所得预测误差结果的实际有效性。

3 总结

综上所述，将有限元分析方法应用到建筑复合地基加固区沉降预测工作中，可以有效地提高预测的精准度，从而为建筑施工提供有价值的参考数据。由于时间的限制，在实践过程中只针对一个项目中的两个复合地基加固区进行分析，因此在未来的工作中需要进一步完善。