一种基于聚类预填充的SVD算法

魏浩， 张伟， 郭新明

(咸阳师范学院 计算机学院， 陕西 咸阳 712000)

0 引言

随着电子商务的快速成长和网络购物的迅速普及，如何使用户在数量庞大的商品中快速、高效地找到他们感兴趣的商品，是电子商务网站面临的一个重大挑战。推荐系统不需要用户主动参与，能根据用户以往的商品购买记录，获得用户兴趣，把用户可能感兴趣的商品进行推荐，满足用户的个性化需求[1-2]。

目前应用最广泛的推荐算法包括基于内容的推荐算法和协同过滤(Collaborative Filtering，CF)算法，协同过滤算法使用用户与商品的历史交互数据，并通过分析其他人的兴趣偏好，建立当前用户偏好模型，这就是“协同”的体现，它基于存在一组兴趣偏好相似的用户群的假设。相比较基于内容的推荐算法，协同过滤算法对音频、图像等难以提取特征的非结构化对象有较好的推荐效果[3-4]。

1 数据稀疏性问题

协同过滤算法根据用户群体社会化的特点，具有高度自动化、新兴趣发现等优势，并且能够对非结构化对象进行推荐，因此在推荐系统中被广泛使用，但它存在稀疏性、冷启动和扩展性等问题[5-7]。在电子商务系统中，由于用户和商品数量的急剧增加，加之用户缺乏对商品评分的主动性，使得用户评分的商品数量只占很少的一部分，用户—商品评分矩阵(表)非常稀疏，用户—商品矩阵的高度稀疏将造成相似计算的很大误差，进而影响推荐系统的推荐质量和推荐性能[8-10]。

解决数据稀疏性问题的主要方法有：降维技术、评分矩阵预填充、多种特征融合、数据聚类和相似度改进算法[11-14]。文献[15]采用奇异值分解技术和随机梯度下降法填充稀疏矩阵，优化用户相似度，提高了推荐算法的有效性。文献[16]首先提取项目属性特征，并利用余弦相似度对评分矩阵的缺失值进行填充，然后通过对填充的矩阵执行奇异值分解 (Singular Value Decomposition，SVD)算法，寻找隐性特征，建立隐语义模型。文献[17]针对数据稀疏问题，选择非精确拉格朗日乘子法对稀疏矩阵填充，对填充的矩阵使用SVD协同过滤算法进行推荐，提高了推荐质量。

2 改进的基于聚类预填充的SVD算法

大多数推荐系统中，用户评过分的项目很少，项目之间的共同评分更少，会使得计算项目间的相似度误差较大，得到的项目近邻集合也有偏差[18-19]，SVD算法一般使用项目评分的平均值填充评分矩阵，平均值填充未考虑不同类别用户对项目评分的差异性，因此会产生较大的误差。针对这种情况本文提出了一种基于聚类预填充的SVD算法(Cluster Pre-filling SVD，CP-SVD)，算法基于聚类的稀疏数据预处理方法，首先由用户历史评分和项目特征生成用户—项目兴趣矩阵，再聚类用户并填充用户—评分矩阵，通过填充后的用户-评分矩阵，再使用SVD算法预测用户对未评分项目的评分，提高预测的精度和推荐的准确度。

在一个推荐系统中，一般包含的项目数量十分巨大，而项目特征的个数要远远小于项目数，例如Movielens-100k数据集，电影的数目有1 682部，而电影的类型只有19种，一部电影可以属于一个或多个不同的类型，用户—电影评分矩阵(用户—项目评分矩阵)的数据稀疏度为0.937。改进的基于聚类的协同过滤推荐算法通过将用户—电影评分矩阵转化为用户—电影类型兴趣矩阵(用户—项目特征兴趣矩阵)，使用用户—电影类型兴趣矩阵聚类用户,并填充用户—电影评分矩阵，大幅降低用户—电影评分矩阵稀疏度。假设一个推荐系统中，包括N个用户和M个项目，R为用户—项目评分矩阵记作[ru,i]N×M，其中ru,i表示用户u对项目i的评分；M个项目、Q个项目特征以及项目—项目特征矩阵V=[vi,f]M×Q，算法生成N个用户对Q个项目特征的用户—项目特征兴趣矩阵T=[tu,f]N×Q。以Movielens-100k数据集为例，算法步骤描述如下。

(1) 数据读入和预处理：读入用户对电影的评分集合，把用户对电影的评分集合分成训练集train和测试集test两部分，使用训练集部分生成用户—电影评分矩阵R=[ru,i]N×M，读入电影的类型描述集合，生成电影—电影类型矩阵(项目—项目特征矩阵)V=[vi,f]M×Q。

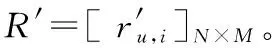
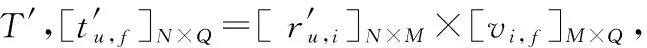
(4) 使用用户—电影类型兴趣矩阵T对用户聚类：将矩阵T的每一行作为一个用户—电影类型兴趣向量，选择K-均值聚类，设定聚类的个数k，进行聚类运算。

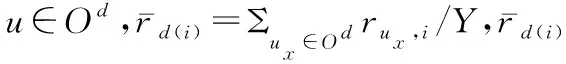
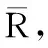
(7) 计算推荐准确率和召回率：依据给定TOP-N的N值生成推荐给用户的电影集合top-N，计算推荐准确率和召回率。

3 实验描述及结果分析

实验使用的编程语言是Python3.7，开发工具为Jupyter notebook，实验程序还使用了两个扩展程序库NumPy和Pandas。NumPy是一个基础性的Python科学计算库，提供高维度数组与矩阵的计算能力，并提供大量方便用户调用的函数库[20]。Pandas是一个数据分析包，通过提供的标准数据结构以及快速、灵活的操作，成为了Python环境下高效而强大的数据分析工具[21]。

实验所使用的数据集是Movielens-100k，由943名线上电影观众针对1 682部电影共10万条评分记录组成。该数据集包含电影的类型描述、用户信息和用户对电影的评分3个数据集文件，电影类型有19种，用户对电影的评分是1到5的整数，每部电影至少被评价1次，每个用户至少给20部电影评过分。原始数据随机分成5份，每次将其中4份数据作为训练数据，另一份作为测试数据，运行5次并将5次实验结果的平均值作为最终的评测值。

实验选择3个推荐算法评价指标包括推荐精度(MAE)、准确率(Precision)以及召回率(Recall)，使用这3个评价指标，将改进的基于聚类预填充的SVD算法(CP-SVD)与SVD算法以及传统的基于项目的协同过滤推荐算法(Item-based CF，ICF)进行比较。ICF算法需要确定的参数是用户K最近邻的K值，SVD和CP-SVD算法共同的参数是保留的信息量δ，CP-SVD算法还需要确定聚类的个数k。

(1) CP-SVD算法聚类的个数k值取5、10、20、30、40，保留的信息量δ取值由0.8至1.0，CP-SVD算法的MAE在k值一定的情况下，随δ值变化趋势如图1所示。

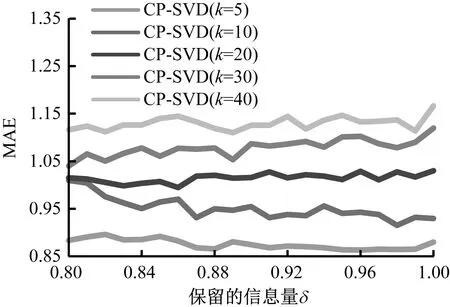
图1 K取值从5到40时CP-SVD算法MAE比较

当k=5时，MAE值随K值的变化曲线位于k等于10、20、30、40四个曲线的下方，说明CP-SVD算法的聚类个数k取值在5附近时，预测精度较高。

(2) 保留的信息量δ取值由0.8至1.0，CP-SVD算法聚类的个数k值取2至6生成的5条MAE值变化曲线及SVD算法的MAE值变化曲线,如图2所示。

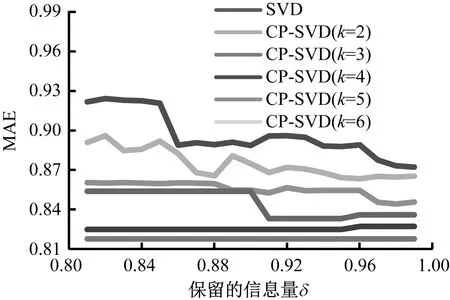
图2 在K取值从2到6时CP-SVD算法MAE比较

从总体来看，k等于5时的曲线位于k等于其他值的曲线下方，说明CP-SVD算法聚类的个数k值取5时，算法预测精度高。

(3) 最近邻数目K值由10到200，且为10的整数倍，ICF算法的MAE值随用户最近邻数目K变化曲线,如图3所示。

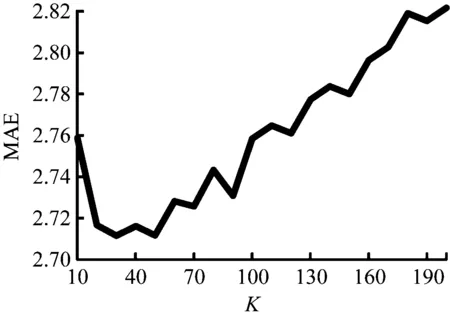
图3 ICF算法MAE随N值变化曲线

当K=30时，MAE值最小，MAE=2.716。

(4) TOP-N推荐的N值取值由10到200，且为10的整数倍，ICF最近邻数K值取30，SVD和CP-SVD算法保留的信息量(δ)为0.99，且CP-SVD聚类个数K等于5，ICF、SVD和CP-SVD三种算法的预测准确率曲线和预测召回率曲线，如图4、图5所示。

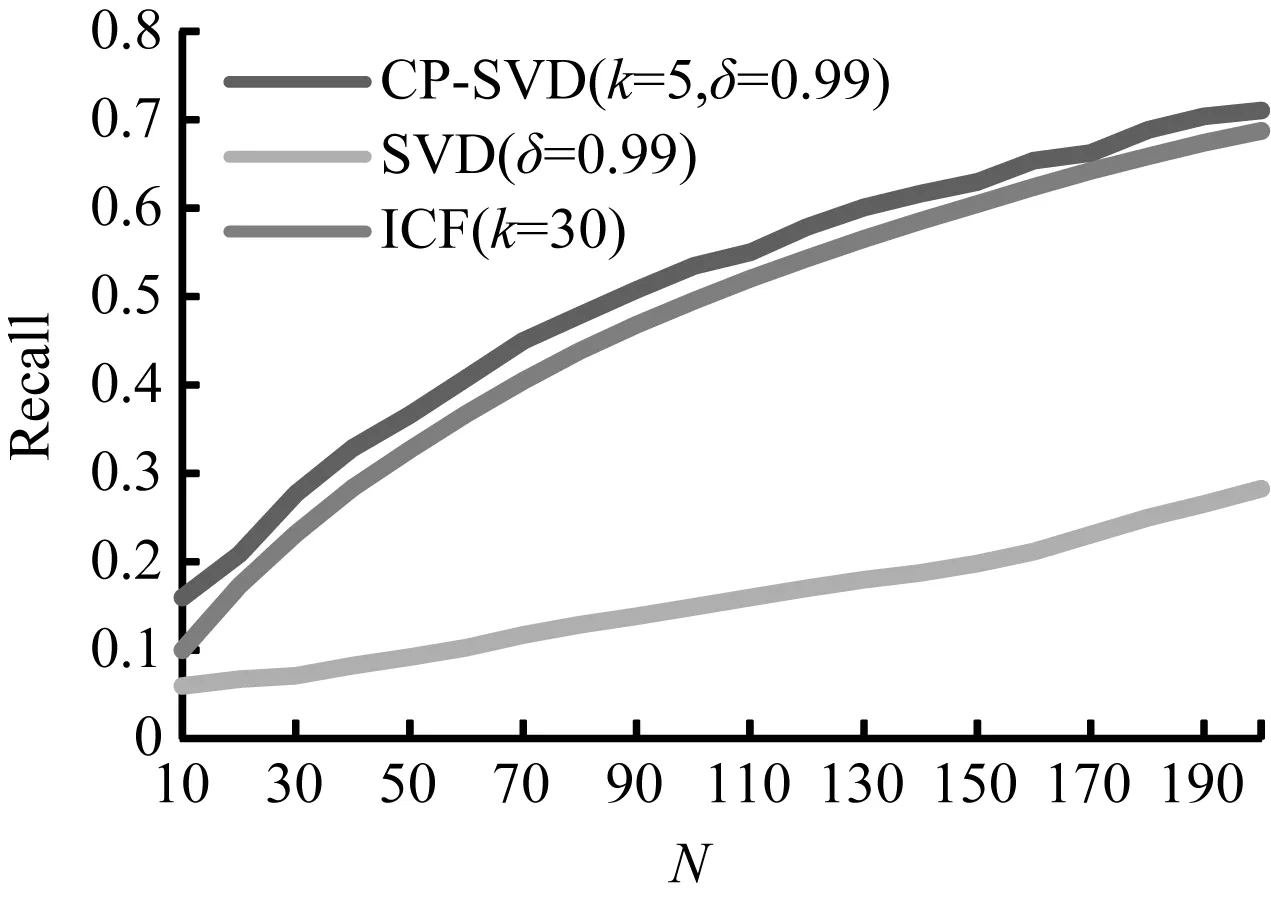
图4 三种算法准确率比较

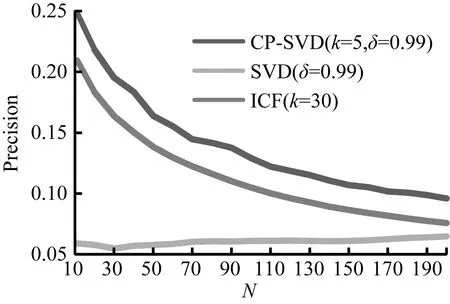
图5 三种算法召回率比较

CP-SVD算法的推荐准确率和召回率远高于CFAASP算法；CP-SVD准确率和召回率随N值变化曲线始终位于ICF算法曲线的上方，在N取值相同时，CP-SVD算法的准确率和召回率高于ICF算法。

4 总结

本文使用Movielens-100k数据集，选择了3个推荐算法评价指标，将改进的基于聚类预填充的SVD算法(CP-SVD)与SVD算法以及传统的基于项目的协同过滤推荐算法(ICF)进行比较。由实验得出聚类个数k=5时的CP-SVD算法的MAE值最小，且小于SVD算法；最近邻K等于30时，ICF算法的MAE值最小；聚类个数k等于5、保留信息量(δ)等于0.99的CP-SVD算法的准确率和召回率，大于保留信息量(δ)等于0.99的SVD算法值及最近邻K等于30的ICF算法。从总体来看，改进的基于聚类预填充的SVD算法(CP-SVD)预测精度、推荐准确率和召回率高于SVD算法以及传统的基于项目的协同过滤推荐算法(ICF)。