基于小波变换随机自排的多次波压制方法研究

张 卫

（长江大学，湖北 武汉 430100）

随着地震勘探理论与技术的不断成熟与发展，地震勘探已经逐渐由浅层向深层、由简单向复杂、由陆地向深海过渡，人们越来越追求一个更加精确的地下构造剖面。地震资料的信噪比是基础，是地震资料处理中最基础、最重要的环节，压制噪音的好坏直接影响到地震剖面解释的准确性。因此提高地震资料的信噪比是地震数据处理中的首要任务，具有非常重要的地位。

多次波是地震资料中一种常见的相干噪音，尤其是在海洋地震数据中，多次波能量强、分布广，导致海洋地震资料信噪比降低，形成构造假象，影响地震勘探的准确性。目前研究较多主要是面波、多次波以及随机噪音，尤其是多次波的衰减[1]，是地震勘探中长期面临的难题。如果处理不当，有效信号的能量将会被这些干扰严重破坏，直接影响地震资料速度分析的精度以及偏移成像的效果，甚至会对后续的地震资料解释工作造成错误的分析。为此，我们需要对地震资料干扰波压制同时最大程度的保留有效信息，这不仅有重要的理论意义和技术价值，还具有实际的应用价值和直接的经济效益。目前压制多次波主要有两大类方法：第一类是基于信号理论滤波法，将含有多次波的地震数据转换到不同变换域，最终将去除多次波后的地震数据反变换到原始数据域中。主要方法有预测反褶积（Robinso）、Radon 变换（Hampson）[2]、F-K 变换（Ryu）等。第二类是基于波动方程预测相减法[3]，其原理是先预测出多次波模型，与原始地震数据匹配自适应相减，从而消除多次波。主要方法有波场外推法（Berryhill）、反馈环法（Verschuur）[4]、反散射级数法（Weglein et al.）等。

本文通过研究线性Radon 变换和抛物线Radon 变换，对两种方法的原理及压制多次波的实现过程进行阐述，在此基础上提出了一种去除多次波新方法。该方法操作步骤：首先对地震数据进行动校正[5]、随机排序、小波变换去噪、反随机排序、反动校正后得到一次波地震数据。通过本文所提方法，压制多次波能量得到很好的效果，在去除多次波的研究中，具有广阔的应用前景。

1 方法原理

地震资料数据进行动校正时，一次波的同相轴基本可以较平，而多次波的同相轴由于动校正不足，会发生弯曲。对校正后的数据进行随机化处理，由于一次波是水平同相轴，随机排序后，一次波的形态不会改变，多次波反射则表现为随机噪声，尤其是和一次波相交的多次波能量团会散落分布在一次波同相轴两侧。基于小波变换方法去除随机噪声，进行反随机排序、反动校正，这样就得到有效波地震数据。

2 数据测试

地震勘探中[6]，如果地下介质的结构不同，则地震波传播的特点也就会不同。本文研究的是水平层状介质下的一次波和多次波。本文合成1000*50 模拟地震数据来测试所提出的方法，图1（a）所示有50 道地震记录，道间距为10m，采样点数为100，采样时间为1000ms，采样间隔为0.001s。

图1（b）是随机排序后效果，可以看到多次波能量团成为了随机噪声；图1（c）是去除多次波后得到的效果图，和一次波相交的多次波都被很好的去除[7]，得到一次波的地震数据。本文运用的方法很好去除了地震数据中的多次波，得到了只含有一次波地震数据，在此过程中，一次波同相轴能量没有较多的损耗也没有丢失的情况。

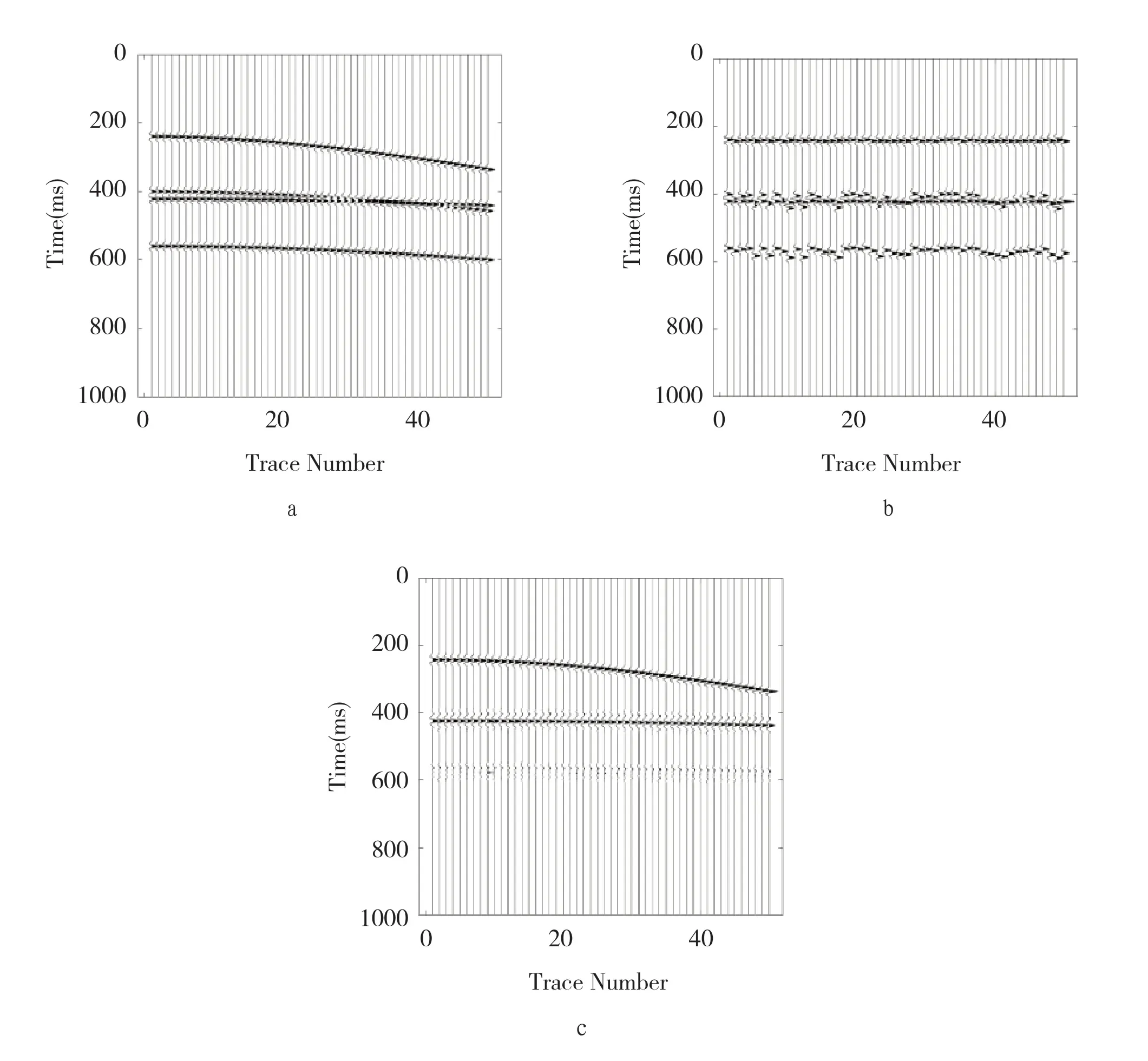
图1 本文方法所对应效果

3 Radon 变换

Radon 变换是对特定数据沿直线、双曲线、抛物线轨道进行叠加。分别称为直线、双曲线、抛物线Radon 变换。通过Radon 变换将数据转换到新的域，在新域中将有效信号和干扰信号所对应的分量分离开，则可以将干扰信号的分量剔除掉，再通过反Radon 变换将处理的数据返回到原来的域[8]，即可达到剔除干扰的目的。在有效波和多次波相交的情况下，时空域很难将它们分离出来，但是变换到Tau-p 域中很容易将它们分离，这大大降低了复杂性。

下面采用的是1000*50 模拟合成的抛物线，如下图2所示。

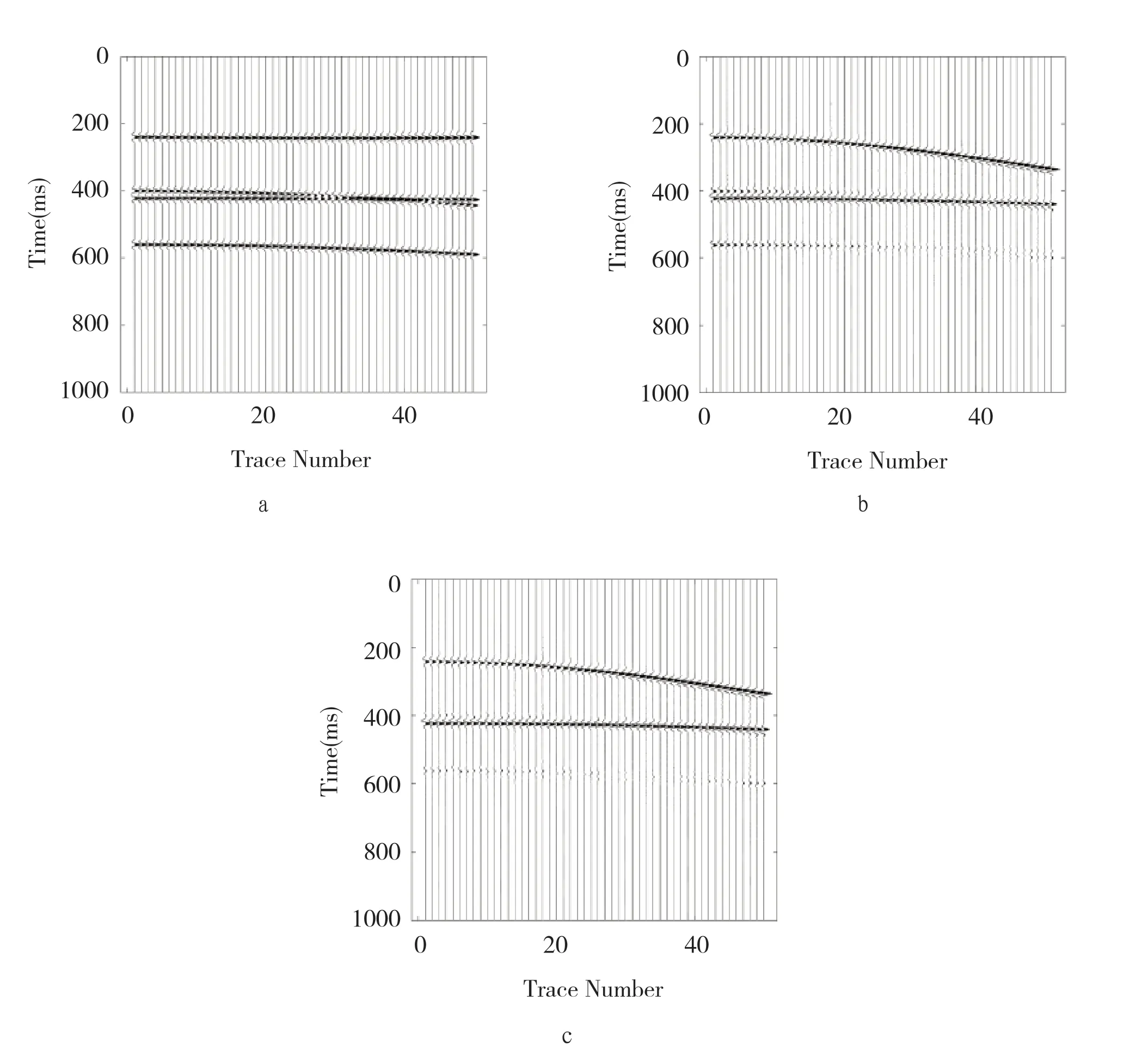
图2 Radon 变换结果

图2（b）线性是Radon 变换后得到的结果，可以看出有大量噪声的存在，在一次波同相轴两侧有少许多次波能量团，可以得出线性Radon 变换效果不是很好。图2（c）是抛物Radon 变换后得到的结果得出，两条一次波的同相轴前端能量比较稀疏[9]，说明在抛物Radon 变换过程中会损耗一次波能量，效果不是很好。两者一次波同相轴前端稀疏，在Radon 变换中有能量损失[10]的情况，前者有多次波能量团的痕迹，两者一次波前端有能量散的趋势；图1（c）前端无稀疏的情况，几乎没有多次波的痕迹。对比而得，图1（c）效果比前两者较好。

4 结论

利用基于小波变换的随机排序的方法压制多次波，在压制多次波方面取得了不错的效果。多次波经过变换成为随机噪声，用小波变换方法去除随机噪声，再经过反随机排序、反动校正操作后得到一次波数据。Radon 变换方法去除多次波是对数据做Radon 正变换，将数据变换到τ-p 域内。然后，利用一次波和多次波的速度差异，在τ-p 域内选用合适的滤波器除去多次波能量。相对比Radon 变换，本文方法不需要变换到另一个域，只需要在时间域内进行操作即可，大大减少了操作的复杂性。所提出的新方法在工业上有广阔的应用前景。