Strain-modulated ultrafast magneto-optic dynamics of graphene nanoflakes decorated with transition-metal atoms∗
2021-09-28YimingZhang张一鸣JingLiu刘景ChunLi李春WeiJin金蔚GeorgiosLefkidisandWolfgangubner
Yiming Zhang(张一鸣),Jing Liu(刘景),Chun Li(李春),3,†,Wei Jin(金蔚),Georgios Lefkidis,,and Wolfgang H¨ubner
1School of Mechanics,Civil Engineering and Architecture,Northwestern Polytechnical University,Xi’an 710072,China
2Department of Physics and Research Center OPTIMAS,Technische Universit¨at Kaiserslautern,P.O.Box 3049,67653 Kaiserslautern,Germany
3Department of Mechanical Engineering,University of Manitoba,Winnipeg MB R3T 5V6,Canada
4School of Physics and Information Technology,Shaanxi Normal University,Xi’an 710119,China
Keywords:graphene nanoflakes,straintronics,spin dynamics,strain effect,first principles
1.Introduction
Graphene nanoflakes(GNFs),arbitrarily shaped graphene fragments that are finite in both dimensions,have emerged as new materials for improving electronic,spintronic,optical,and sensing devices.[1–4]They have potential applications due to the fact that they can be cut into a large variety of different shapes,due to quantum confinement and variation of the edges.[5,6]Mono-layer and multi-layer GNFs can be generated with different techniques.[7–9]When a graphene sheet is cut into fragments,the created edges strongly affect the electronic structure of graphene depending on the geometry of edges(zigzag and armchair).The presence of a zigzag edge state,accompanied by a large local density of states(LDOS)and localized spins,plays an important role in the electronic,magnetic and chemical activities to graphene edges and nanosized graphene.[10]Furthermore,GNFs with all zigzag boundaries,such as triangulene,[11]rhombic GNFs[12,13]and Clargoblet nanographene,[14,15]have been synthesized with several scalable synthetic methods and possess excellent magnetic properties.Such graphene nanoflakes with zigzag edges attract interests for their applications in spintronic devices.[16,17]
However,the gapless nature of graphene[18]limits its applications in fabrication of novel electronic devices.A substantial amount of theoretical and experimental works have predicted that adsorption of transition metal atoms on graphene can effectively induce and tune band gaps of GNFs.[19–23]It is worth noting that the transition metal atoms(TM-atoms)doped graphene structures have been synthesized experimentally with satisfactory stabilities.[24–27]Previous studies have,without exception,expounded that doped TM-atoms can also significantly manipulate the electronic and magnetic properties of graphene.[28,29]Actually,both the low binding energy of TM-doped graphene and the strong bonds between the adjacent carbon atoms and the TM atom greatly affect the magnetic properties.For instance,the strong bonds between the carbon atoms and the TM-atoms lead to the localization of theπorbits near the Fermi levels;[30,31]3d atoms such as Co,[32]Cr,[33]and Fe[28]give rise to magnetic moments in monolayer graphene.Combining GNFs and TMatoms,the GNFs can provide ultrafast electronic charge transport and the magnetic elements act as information carriers,which could introduce new two-dimensional(2D)spintronic devices and applications.
Strain is another effective method to modulate physical properties of 2D materials.[34–37]As is well-known,strain in graphene has been proposed as a tool for modifying its electronic structure and physical properties.For instance,both experimental[39,40]and theoretical[41]studies demonstrate that the ultrafast magnetization dynamics in fcc Ni can be manipulated with pressure.The essence of strain is to change the geometry and thus affect the electronic structure of the system.[42]In TM-doped GNFs,the magnetism of the structure is mainly induced by the interaction between the TMatoms and the adjacent carbon atoms.Therefore,altering the bonds between the TM-atoms and the GNF can effectively adjust the electromagnetic characteristics of the system and more intuitively reflect the internal mechanism of the strain modulation.
These investigations stimulate us to explore the local deformation effects on the laser-induced spin dynamics on TM&GNFs(TM=Fe,Co,Ni)structures.We find that the spin-flip processes on TM&GNFs take advantage of the synergy effect of the TM-atom species and the position where the TM-atoms are attached to the nanoflake(TM-adatoms on the edge or vertex of the rhombic graphene nanoflake).Moreover,by applying strain along the C–Ni bonds,we have calculated the strain effect on the spin-flip process in the Ni&GNF structure.It shows that the increasing strain along the C–Ni bonds can significantly promote the spin-flip processes in Ni&GNF structures owing to the better selection rules for increased bond lengths.The present results offer a promising way to actively control spin,which can lead to more flexibility in the functionalization of future straintronic devices.
2.Theory and method
Our calculations are based on an ab initio quantum many-body model termed“Λprocess”.[43–45]In our previous studies,we demonstrated thatΛprocesses can act as exact microscopic spin-transition mechanisms on ultrafast,laser-induced,magnetization-dynamics scenarios.[46–50]This theoretical model also applies to magnetic molecules and low-dimensional carbon structures.[51–54]Especially,a longdistance ultrafast spin transfer model over one-dimensional carbon chain structure has been proposed very recently.[55]
In our calculations,the Hamiltonian of strongly correlated systems is solved in four distinct steps.[56,57](i)The first approximate geometry optimization of the system at the Hartree–Fock level.This serves as a starting geometry for the subsequent more detailed geometry adjustments,and produces the electronic reference states for the subsequent post-Hartree–Fock calculations.
(ii)A series of highly correlational post-Hartree–Fock calculations,typically with the symmetry-adapted cluster configuration interaction(SAC-CI)method.[58]Such a method represents at the moment the best compromise between accurate calculations of magnetic properties and reasonable computation time,and at the same time provides a balanced way of including both dynamical and static correlations.
(iii)Perturbative inclusion of relativistic effects(notably spin-orbit coupling).This step is at the very core of our methods,because all our suggested laser-induced scenarios necessitate spin-mixed intermediate electronic excited states,which are optically coupled to both the initial and final states(Λprocesses).At this step we concurrently include an infinitesimal static external magnetic field,which allows us to energetically differentiate between the spin-up and spin-down states(Zeeman splitting).Here we can already distinguish the initial and final states for local spin-flip process.The idea of spin-flip process is that,to generate a fast transition between two almost degenerate states(within Zeeman splitting)with opposite spin directions,we need a laser excitation to a highly excited state,which is a spin-mixed state due to spin–orbit coupling,and subsequently undergoes a de-excitation to the state of opposite spin.

3.Adsorption of TM-adatoms
3.1.Structural optimization
Since the rhombic GNFs have been synthesized,[12,13]there have been three types of TM-doped monolayer GNFs reported.(i)The TM atoms are doped on the boundaries of GNFs,[61–63]in which the TM atoms are doped on the edge of monolayer GNFs,and the TM atoms prefer staying in the plane.(ii)The metal impurities are involved by substituting carbon atoms in graphene,[64]that is,several C atoms are replaced by magnetic atoms,and the magnetic atoms will keep a certain distance out of the plane.(iii)The magnetic atoms are placed perpendicular to the GNFs(π-conjugated graphene),where the magnetic elements interact with the C atoms on the hexagon carbon rings,and the TM atoms prefer positions above the hollow sites of the hexagon carbon rings.[65–67]Among these three types of TM-doped monolayer GNFs,we investigate the structures with TM atom decorated on the GNFs boundaries,and construct the TM&GNFs(TM=Fe,Co,Ni)structures to study the spin dynamics of the two types of TM&GNFs(TM=Fe,Co,Ni),owing to their high degree of spin-density localization and narrow band electronic structures,thus allowing for coherent spin manipulation.As shown in Fig.1,when a magnetic atom is absorbed on the graphene nanoflake,the obtained structures can be classified into two types with respect to the connecting position:(i)TM-adatoms connected to one of the C atoms at the zigzag edges;(ii)TM-adatom on the vertex of the rhombic graphene nanoflake.

Fig.1.Optimized(a)V-type and(b)VT-type TM&GNFs structures.(c)Sketch of the strain model for the VT-type TM&GNF.
Before we investigate the spin dynamics of the two types of TM&GNFs(TM=Fe,Co,Ni),all the structures are fully relaxed to obtain a balanced structure,the stability of each structure is confirmed by the calculated normal mode with the absence of imaginary frequencies.The binding energy of the TM&GNFs structures are listed in Table S1 in the supplementary materials.After optimization,two types of structures are further studied,noted as V-type[Fig.1(a)]and VT-type[Fig.1(b)],respectively.Furthermore,we probe the geometry deformation after doping the magnetic elements,which is discussed in Section 1 in the supplementary materials.It is noteworthy that since Li et al.found reduced resistance and more active electromagnetic properties by removing the H atoms on the boundaries of graphene nanoflakes,[12]we do not add H atoms on the boundaries in the present calculations.
3.2.Spin density
Before calculating the time-dependent spin-flip process,it is necessary to check the spin density distribution of each equilibrium structure.Based on theΛprocess theoretical model,we need to identify the states with adequate spin localization,which could be the initial and final states of the spinflip processes.To this end,we calculate the spin density on each many-body state using Mulliken population analysis.It is noteworthy that,although this analysis only gives an estimate of the spin distribution in our structures,it is sufficient to detect which atoms and states carry the spin.
Table 1 shows the spin density in the TM&GNFs(TM=Fe,Co,Ni)configurations for the lowest five triplet states,while the initial and final states will be selected from one of the spin localized triplet states.The energy levels of the TM&GNFs structures are listed in Fig.S1 in the supplementary materials.In addition,the spin configuration of the lowest five triplet states of V-and VT-type structures are listed in Tables S2 and S3,respectively.An important advantage of triplet over doublet ground states is that a triplet is built from two electrons:using triplet states we can separate spin and charge dynamics.[42,48,51,53]Compared to the spin distribution,we find that the spin is localized mostly on the TM atoms for state 1.Although the spin distribution in the ground state of Fe&GNF is not as high as in Co&GNF or Ni&GNF,it is yet by far higher than on the C atoms.Moreover,compared the spin distribution with different TM-atoms,degree of spin localization in Ni&GNF is higher than for Co&GNF and Fe&GNF.For instance,in the V-type structures for the ground state,the spin density of the Ni atom in Ni&GNF is 1.830,which is higher than the values in Co&GNF(1.782)and Fe&GNF(1.793).As for the VT-type structures,Ni&GNF also attains the leading position of spin distribution,indicating higher spin polarization and more pronounced magnetism.In addition,for the purpose of experimental realization we want the initial and final states to lie energetically as low as possible.Therefore,we choose the spin-down(|↓〉)and spin-up(|↑〉)substates stemming from triplet state 1 as the initial and final states in the further spin dynamics study.

Table 1.Spin density(without SOC)in the TM&GNFs(TM=Fe,Co,Ni)configurations for the lowest five triplet states.
3.3.Spin flip on TM&GNFs(TM=Fe,Co,Ni)
Based on the spin density analysis of the two types of TM-atom doped structures(V-and VT-type)in the previous section,the triplet ground state fulfills the requirement of aΛ process.The spin-down(|↓〉)and spin-up(|↑〉)states stemming from the triplet ground state are chosen as the initial and final states for spin-flip processes.Moreover,the spin angular momenta of states|↓〉and|↑〉have the same absolute values and the opposite directions,satisfying the selection requirements of the initial state and the final state.[68]
Figures 2 and 3 show the spin-flip processes obtained in the two types of configurations with three different TMadatoms,all of which complete within subpicoseconds with high fidelity above 96%.For each scenario,the upper panel depicts the occupation probabilities of the involved states and the lower panel depicts time-resolved expectation values of the spin components.

Fig.2.Spin-flip processes achieved on the V-type(a)Fe&GNF,(b)Co&GNF,and(c)Ni&GNF structures.For each scenario,the upper panel depicts the occupation probabilities of the involved states(initial:black dashed,final:red solid,intermediate:dash-dotted),and the lower panel shows the time-dependent expectation values of the spin components.The insets give the envelopes of the optimized laser pulses.

Fig.3.Spin-flip processes achieved on the VT-type(a)Fe&GNF,(b)Co&GNF,and(c)Ni&GNF structures.For each scenario,the upper panel depicts the occupation probabilities of the involved states(initial:black dashed,final:red solid,intermediate:dash-dotted),and the lower panel shows the time-dependent expectation values of the spin components.The insets give the envelopes of the optimized laser pulses.
Comparing the spin-flip processes achieved in V-and VTtype structures,first,the spin-flip processes completed in the V-type structures are obviously faster than those in the VTtype structures.For a more intuitive comparison,Table 2 lists the parameters for each spin-flip process,where the FWHM(full width at half maximum of the laser pulse)is close to half the time needed to complete the flip processes.Here we compare the FWHM to illustrate the time for spin-flip processes.The FWHMs for Fe-,Co-,and Ni-decorated V-type structures are 92.27,284.27,and 245.28 fs,respectively,while for the VT-type structures,the corresponding magnitudes climb to 225.91,510.38,and 473.28,respectively,almost twice the V-type ones.Moreover,it is noteworthy that in both the Vand VT-type structures,the time required to achieve a spinflip process for three different TM-atoms increases in the order of Fe,Ni,and Co.Santos et al.[64]have pointed out that the Fe atom in graphene holds different magnetic properties compared with other transition metal atoms due to the complex band structure.For Co and Ni doped graphene nanoflakes,the electronic levels of Co&GNF and Ni&GNF contain more contributions of carbon character,which lead to the small oscillatory spin moments.Owing to the different bonding states between the GNFs and Fe,Ni,Co atoms,the spin-flip processes in TM&GNFs structures can be effectively modulated by different TM adatoms.
Furthermore,we compare the energy of the laser pulse(Table 2).With the same adatoms,the energy of of the laser pulse is influenced by the synergy effect of the number of oscillation cycles in the population propagation,the number of involved intermediate states and the occupation of intermediate states.For instance,when the TM adatom is Fe,the energy of laser pulse is 0.687 eV for the VT type and 0.685 eV for the V type.For the Ni&GNF systems,the energies of the laser pulse are 0.419 eV(V-type)and 0.593 eV(VT-type),which is mainly caused by the occupation of the intermediate state(37%for V-type and 75%for the VT-type systems).In the Codecorated systems,the energies of laser pulse increase from 0.451(V-type)to 1.696 eV(VT-type).

Table 2.Optimized laser parameters for each spin-flip scenario.Hereθandφdenote the angles of incidence in spherical coordinates,andγis the angle between the polarization of the light and the optical plane.FWHM is the full width at half maximum of the laser pulse.
In order to further reveal the underlying mechanism,we also examine the highest occupied molecular orbital(HOMO)energy levels of the system(Fig.4).It is obvious that the electron clouds are localized around the Ni atom in the VTtype structures,while the V-type structures produce a completely different picture with the electron cloud distributed in the GNF.However,from the analysis of the spin density in the equilibrium structures,the spin density for the ground state is always localized on the Ni atoms in both V-and VT-type structures.This indicates that in the V-type structures,the applied laser pulse mainly affects the spin properties of the system without electronic interference.For the VT-type structures,both the spin and the charge are excited during the local spinflip processes obtained in the Ni atom,which could significantly slow down spin-flip processes.The lower energy and shorter time in the V-type structures demonstrate low-energy consumption and efficient logic operation processes.

Fig.4.The electron clouds of the HOMO of(a)V-type and(b)VT-type equilibrium Ni&GNFs.The isosurfaces of the wavefunctions are red and green for positive and negative values,respectively.The isovalue is 0.02.
4.Local deformation effect on Ni&GNF
4.1.Structural reoptimization
We have revealed the temperature-dependent,phonongenerated geometric distortions of the symmetry,the optical effects,and the laser-inducedΛprocesses[45,69,70]in the past.In the present study,we introduce the local deformation to the magnetic molecule systems(Ni&GNF),to actively tune the spin-manipulation scenarios.As mentioned in the above section,among the three TM-atom doped GNFs,the total energy of the Ni&GNF is the lowest,and thus is the most stable equilibrium structure.Based on the spin density analysis,Ni&GNF holds the leading position of spin distribution in both V-type and VT-type structures,indicating higher spin polarization and magnetism,so Ni&GNF is studied in the following part for the local deformation effect.
In order to apply the strain on the C–Ni bond of the Ni&GNF systems,we firstly vary the coordinates of the C and Ni atoms along the directions of the applied strain proportionally to their values[Fig.1(c)].Then,the structures are reoptimized to obtain the deformed geometries.To fix the local distortions on the C–Ni bonds,we keep the coordinates of the relevant atoms as constants during the optimization.Except for the fixed atoms,all the other atoms are allowed to geometrically relax to construct stable structures.
It is known that the theoretical C–Ni bond length is 1.82˚A.However,in chemical compounds,the bond length often varies greatly.Many theoretical and experimental studies show that the C–Ni bond length generally lies between 1.8 and 2.0˚A.[71–74]In our present work,the maximum C–Ni bond length is 2.103˚A(in 10%strain),slightly larger than the values in previous works.Nevertheless,as a theoretical prediction,and considering the possibility of the experiment to the greatest extent,it is still worth testing.For instance,Santos et al.increased the spin moment in TM-doped GNFs by stretching the C–Fe bond by 9%,[64]which is just similar to the present work.Based on the above data,we apply a strain from−10%to 10%with 2.5%increment on the C–Ni bonds.That is,the C–Ni bond lengths range between 1.655˚A and 2.023˚A in the V-type structures and from 1.721˚A to 2.103˚A in the VT-type systems.The bond lengths and total energies of the optimized structures are listed in Table S5 in the supplementary materials.Moreover,as is expected,the local deformation can slightly break the geometric stability of Ni&GNF,since the total energy increases with increasing tensile or compressive strains.
4.2.Local deformation effect on spin density
Table 3 lists the Mulliken spin density distribution of the lowest five triplet states in the equilibrium and distorted Ni&GNF structures.The detailed information of the initial and final states(including their energies and spin expectation values)for the spin-flip processes of the strained VT-and Vtype Ni&GNFs are listed in Table S4 in the supplementary materials.In the V-type structures,the spin density for the ground state is always localized on the magnetic elements.With strain increasing from−10% to 10%,the degree of spin-density localization gradually increases.However,for the VT-type structures,when the strain applied to the C–Ni bond is−10%,state 3 is the lowest localized triplet state,and the spin density on the ground state is almost homogeneously localized on the carbon atoms.When the applied strain ranges from−2.5%to 10%,the Ni atom carries most of the spin density,and its value is monotonously increasing.Note that with the same strain increment,in the ground state,the spin density increases more quickly in the VT-type structures,indicating a more obvious strain effect.According to the theoretical requirement of aΛprocess,the spin density distribution for initial and final states should be ultimately localized on the magnetic center.Therefore,in the subsequent spin-dynamics calculations,we still use the spin-down and spin-up states stemming from the triplet ground state 1 as initial and final states for each distorted structure.That is,the applied strains from−10%to−5%will not be further studied for the VT-type structures.

Table 3.Mulliken spin density in the V-and VT-type equilibrium and distorted structures for the five low-lying states,the maximum value for each structure is in bold.
4.3.Spin-flip processes
Based on the analysis of the spin density distribution in the previous section,we focus on the modulation effect of local deformation on the spin-flip process of Ni&GNFs.Figures S3 and S4 in the supplementary materials show the spinflip processes of V-type and VT-type Ni&GNF structures under different magnitudes of strain along the C–Ni bond.The corresponding parameters of the laser pulses are listed in Table 2.It is found that the time is obviously reduced with strain,but the rate of reduction is not identical.For comparison,we show the relationship between the duration(time consumption for spin-flip processes)and strain in Fig.5.It is shown that increasing the distance between magnetic elements and GNF is beneficial to the spin-flip processes,while the strain along the bond in the vertex of GNF(VT-type)can manipulate the spin dynamics behavior even more efficiently.
The strain-promoted spin-flip processes in Ni&GNFs structures convincingly show that the Ni-GNFs hybridization is the key parameter in explaining the magnetic state of Ni doped GNFs.Since the Ni doped GNFs present non-magnetic character,by increasing the C–Ni bond lengths,we firstly change the local electronic properties in Ni&GNFs structures,and then influence the energy levels and energy gap(including the HOMO-LUMO energy gap)of the systems.Thus,we reduce the energy penalty for promoting the electrons between the initial/final state to the intermediate states.Furthermore,increasing the C–Ni distance can manually reduce the interaction between the Ni and carbon atoms,so that the magnetic properties of Ni atom get significantly enhanced,and thus affect the spin-flip processes in Ni&GNFs structures.
To further explore the physical mechanism of the strain effect on the V-and VT-type structures,we calculate the HOMO(highest occupied molecular orbital)and LUMO(lowest unoccupied molecular orbital)energies of the strained Ni&GNF structures(Table S5 in the supplementary materials).The lowest 31 energy levels are calculated and listed in Fig.S2 in the supplementary materials.It is interesting that the HOMO and LUMO energies change gradually with the increasing bond length,while the HOMO going up and LUMO going down.The HOMO energies change faster than the LUMO energies,for instance,in the VT-type structures,the energies of HOMO increase from−4.764 eV to−4.478 eV,with 0.286 eV increment,while the energies of LUMO change 0.033 eV(from 0.584 eV to 0.551 eV),indicating that the HOMO energy level determines most of the virtual excitations,constituting the correlations in the many-body wavefunctions.Moreover,since the HOMO energies go up and the LUMO energies go down with increasing C–Ni bond lengths,it is obvious that the HOMO-LUMO energy gap decreases with increasing C–Ni distances.The decreasing HOMO-LUMO energy gap is accomplished with the increased electronic activity of the system,which could facilitate the transitions between the initial/final state and the intermediate states,thus prominently influence the spin dynamic behavior.
At the same time,it is noteworthy that the strain effect of HOMO-LUMO energy gap(ΔEHOMO−LUMO)is more obvious in the VT-type structures.TheΔEHOMO−LUMOdecreases 0.249 eV(from 5.278 eV to 5.029 eV)with the strain increases from−2.5% to 10%,while in the V-type structures,the value decreases 0.242 eV(from 5.004 eV with−10%strain to 4.762 eV with 10% strain).It is obvious that the HOMO-LUMO energy gap decreases with a higher slope in the VT-type structures,with the same trend as the interaction between the strain and the duration(Fig.5).The strain along the C–Ni bonds in the VT-type structures can efficiently manipulate the HOMO-LUMO energy,thus dominating the spin dynamics behavior more effectively.
From the above results,we find that the spin-flip process in Ni&GNF can be modulated by applying uniaxial strain.Nevertheless,the symmetric tensile and compressive strains do not result in symmetric spin-flip scenarios.The tensile strain can speed up the spin-flip process,while the compressive strain slows down the process.
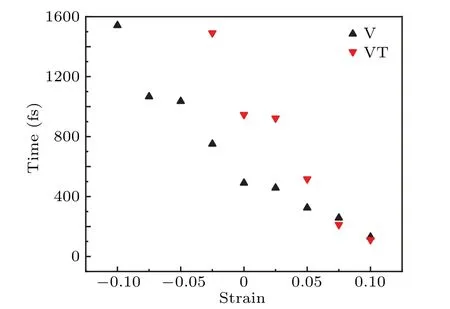
Fig.5.Duration for spin-flip processes of VT-type(red inverted triangles)and V-type(black regular triangles)Ni&GNFs under different strains.
5.Conclusions
In summary,the laser-induced ultrafast spin flip on the TM&GNFs(TM=Fe,Co,Ni)is investigated using theΛprocess-based theoretical model and ab initio calculations,and the spin-dynamics behavior induced by the variation of the C–Ni bond length is investigated in detail.The following conclusions can be drawn in this work.
(i)The spin-flip processes on TM&GNFs are strongly related to the connecting positions.When the magnetic center is a Ni atom,it takes 940 fs and 500 fs in the VT-type and V-type structures,respectively.Similar situations can also be found in Fe&GNF and Co&GNF structures.
(ii)Different magnetic atoms(Fe,Co,and Ni)can significantly change the spin properties,which results from the different binding states of Fe,Co,and Ni.The spin density redistributes with different magnetic centers and the spin flip in Fe&GNF is the fastest for both V-and VT-type structures.
(iii)In the Ni&GNF structures,the spin-flip process can be modulated by the local strain along the C–Ni bonds.The time scale for spin-flip processes decreases with the increasing C–Ni bond length,owing to the better selection rules for increased bond lengths.Especially,the effect of local strain on the spin flip of VT-type structures is more pronounced than that of the V-type structures.When the C–Ni bond of the VTtype structure is stretched to 110% of its equilibrium length,the fastest spin-flip process is achieved within 80 fs.
The theoretical results obtained in the present work provide the precursory guidance for further study of ultrafast magnetization control in GNFs,which can lead to more potential applications in future integrated straintronic devices.
Acknowledgment
GL gratefully acknowledges the hospitality of the Northwestern Polytechnical University,Xi’an,China,during the summer semester 2019.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Multiple solutions and hysteresis in the flows driven by surface with antisymmetric velocity profile∗
- Magnetization relaxation of uniaxial anisotropic ferromagnetic particles with linear reaction dynamics driven by DC/AC magnetic field∗
- Influences of spin–orbit interaction on quantum speed limit and entanglement of spin qubits in coupled quantum dots
- Quantum multicast schemes of different quantum states via non-maximally entangled channels with multiparty involvement∗
- Magnetic and electronic properties of two-dimensional metal-organic frameworks TM3(C2NH)12*
- Preparation of a two-state mixture of ultracold fermionic atoms with balanced population subject to the unstable magnetic field∗
