Quantum multicast schemes of different quantum states via non-maximally entangled channels with multiparty involvement∗
2021-09-28YanYu于妍NanZhao赵楠ChangXingPei裴昌幸andWeiLi李玮
Yan Yu(于妍),Nan Zhao(赵楠),†,Chang-Xing Pei(裴昌幸),and Wei Li(李玮)
1State Key Laboratory of Integrated Services Networks,Xidian University,Xi’an 710071,China
2Cloud Computing Center of Xi’an Branch of Shaanxi Telecom,China Telecom,Xi’an 710002,China
Keywords:quantum multicast communications,non-maximally entangled states,remote state preparation
1.Introduction
Quantum entanglement as a significant quantum resource plays an essential role in the field of applications of the quantum information science,and the theory and technology have achieved some breakthroughs.[1–5]By utilized a shared entangled state,quantum teleportation(QT)[6]is firstly proposed to transmit an unknown qubit from one site to another.Subsequently,Lo[7]gave another intriguing method called remote state preparation(RSP)to transmit a pure known quantum state.Compared with teleportation,RSP requires less classical communication cost,and the sender knows the complete knowledge about the state.Owing to its advantages and features,RSP has been investigated by researchers theoretically and experimentally.[8–19]Further,RSP is extended to multiparty quantum information transmission of multiqubit entangled states,and related schemes are proposed via different quantum channels,[20–25]including maximally entangled and non-maximally entangled.Apparently,the optimal success probability and fidelity can be achieved with the help of the maximally entangled one.However,due to the unavoidable interaction between the quantum channel and its ambient environment,it is difficult to generate and maintain the maximally entanglement.So far,the research of multiparty RSP via non-maximally entangled channels has made dramatic progress.[26–32]
Recently,Chen et al.[28]put forward the controlled RSP of two-qubit state using an eight-qubit partially entangled channel.In 2017,a multiparty RSP scheme was introduced in Ref.[29]where the channel consists of two sets of GHZ states.In 2018,Wei et al.[30]gave a probabilistic controlled RSP with multiparty based on non-maximally entangled state.In 2019,a multicast scheme[31]employing the eight-qubit nonmaximally entangled channel was given for transmitting different two-qubit state to two receivers synchronously.In 2020,Zhao et al.[32]utilized a six-qubit partially entangled channel to broadcast the arbitrary single-qubit state to three remote receivers.Moreover,cluster state is the specific entanglement and can be efficiently applied to information processing tasks.In general,a cluster state is expressed as[33]


2.The multicast scheme of different fourqubit cluster-type states via twelve-qubit nonmaximally entangled channel
Firstly let us name the two receivers Bob and Charlie,while the sender remains Alice.Suppose Alice intends to help Bob to prepare|µ1〉and to help Charlie to prepare|µ2〉synchronously.Here|µ1〉and|µ2〉are given by
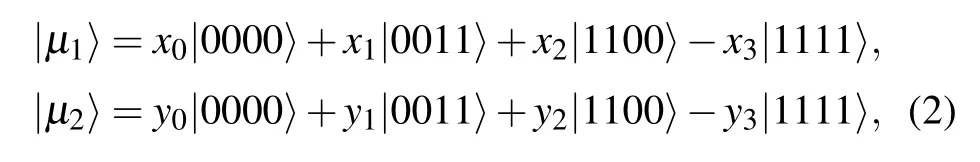
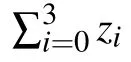


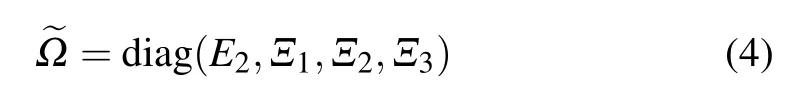

[(S2)]A projective measurement(donated as MA)is performed by Alice on particles(A1,A2,A3,A4)under a set of orthogonal bases{|ε1〉...|ε16〉},which composed of the computation basis{|0000〉,|0001〉,...,|1111〉},

Here construct a 4×4 matrix M(z),

and
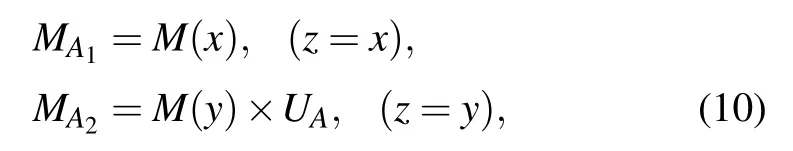


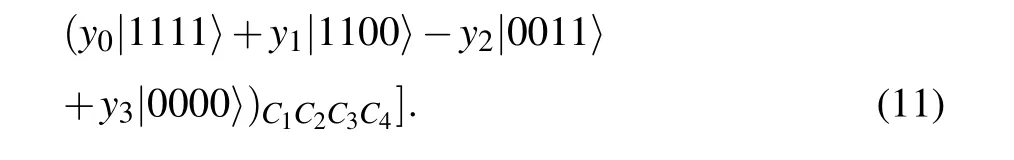
[(S3)]In response to the different measurement outcomes of sender Alice,receiver Bob operates on his qubits(B1,B2,B3,B4)with an appropriate unitary transformation UB,and Charlie reconstructs the state UCas well.All the situations are shown in Table 1.
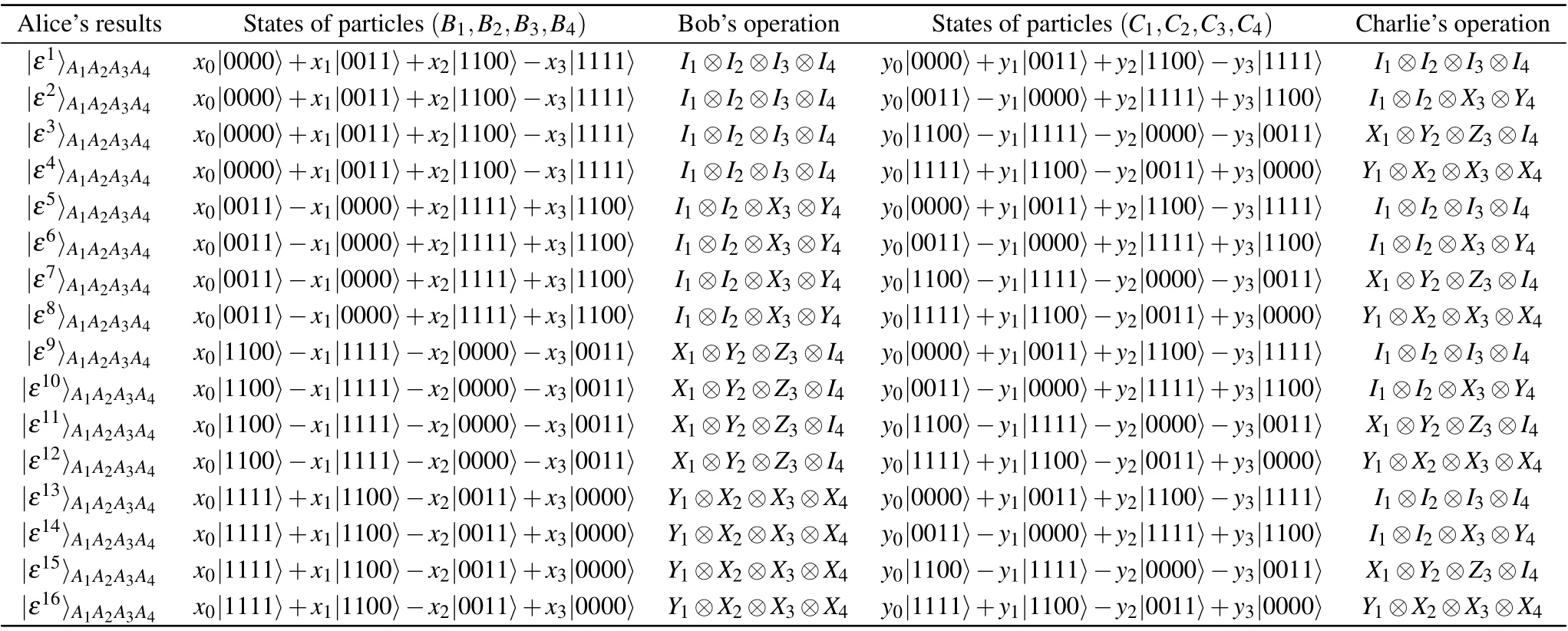
Table 1.Measurement results and unitary operations of each party in multicast scheme of arbitrary four-qubit cluster states via twelve-qubit non-maximally entangled channel.

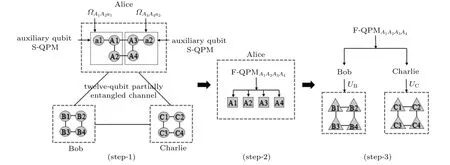
Fig.1.Schematic diagram for the multicast scheme implementation of(S1)–(S3).A twelve-qubit non-maximally entangled state is used as the quantum channel.S-QPM and F-QPM stand for the single-and four-qubit projective measurements,which are performed by Alice.UB and UC stand for the appropriate unitary operations on particles(B1,B2,B3,B4)and(C1,C2,C3,C4),respectively,which are performed by Bob and Charlie.
3.The deterministic multicast scheme of arbitrary single-and two-qubit states via the ninequbit non-maximally entangled channel
Supposed that there are four parties,under the control of the supervisor David,sender Alice would like to assist receiver Bob remotely in the preparation of the arbitrary single-qubit state|ν1〉and assists receiver Charlie in the preparation of the arbitrary two-qubit states|ν2〉,

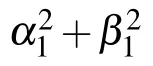
To accomplish the task of this protocol,three nonmaximally entangled quantum resources shared by four participants are shown as follows:
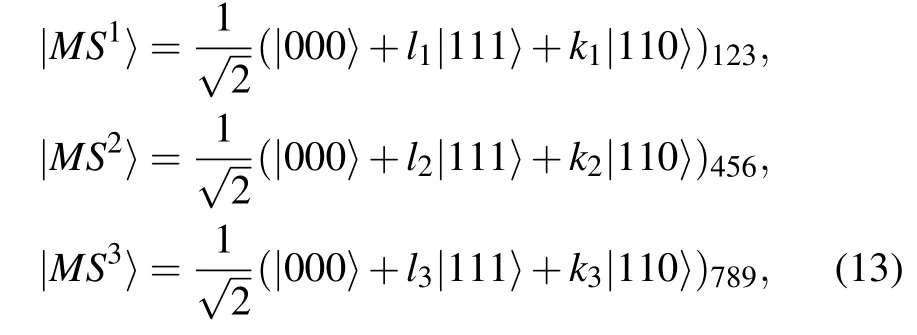

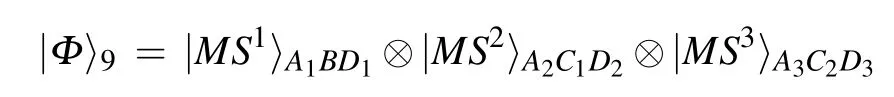

The detailed steps of the deterministic multicast scheme via the non-maximally entangled quantum channel are shown in the following.
[(S1)]A projective measurement is made by Alice on particles(A1,A2,A3)in the orthogonal basis{|εi〉}(i=1,2,...,8)composed of computational bases{|000〉,|001〉,...,|111〉},

where MAin Eq.(15)is taken to be
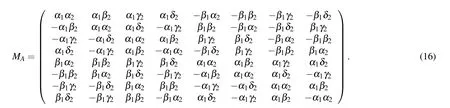
While Eq.(14)can also be of the form
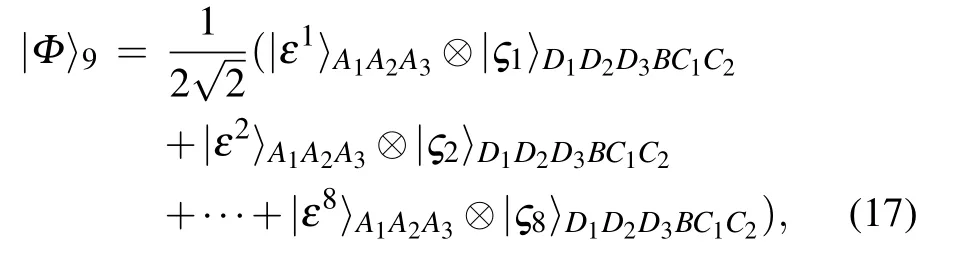
where|ς1〉is taken as an example,i.e.,

After sender’s projective measurement,by classical communication,she broadcasts her measurement outcomes to Bob and Charlie synchronously.
[(S2)]If controller David consents to provide the assistance,he will perform three measurements on particles D1,D2,D3in the following bases synchronously,

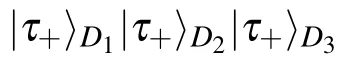


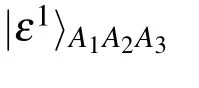

Table 2.Measurement results and unitary operations of each party in deterministic multicast scheme of arbitrary single-and two-qubit states via the nine-qubit non-maximally entangled quantum channel under the orthogonal basis vectors|ε1〉A1A2A3.

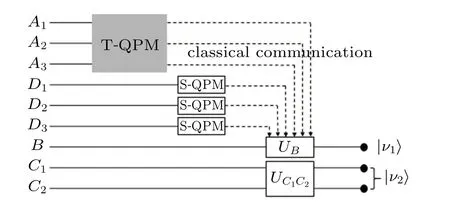
Fig.2.Schematic quantum circuit for deterministic multicast scheme of arbitrary single-and two-qubit states via the nine-qubit non-maximally entangled quantum channel.S-QPM and T-QPM denote single-and three-qubit projective measurements under a set of complete orthogonal basis vectors and{|τ〉}D,respectively.UB and stand for the appropriate unitary operations on particles B and(C1,C2),respectively,which are performed by receivers.
4.Discussion and comparison
According to the theoretical analysis in Sections 2 and 3,by non-maximally entangled channel,we propose two quantum multicast schemes including one sender and multiple receivers,which enable each receiver to obtain different quantum states synchronously.Next,we will give the discussion and comparison about our schemes by the following two aspects.
4.1.Success probability
In this section,we will analyze the success probabilities of two schemes,which are mathematically expressed as follows.For the first one,the total success probability(TSP1)reads

The relationship between the total success probability(TSP)and parameters(ζ0andη0)is shown in Fig.3.If the parameters are chosen at the beginning,the channels will become maximally entangled.
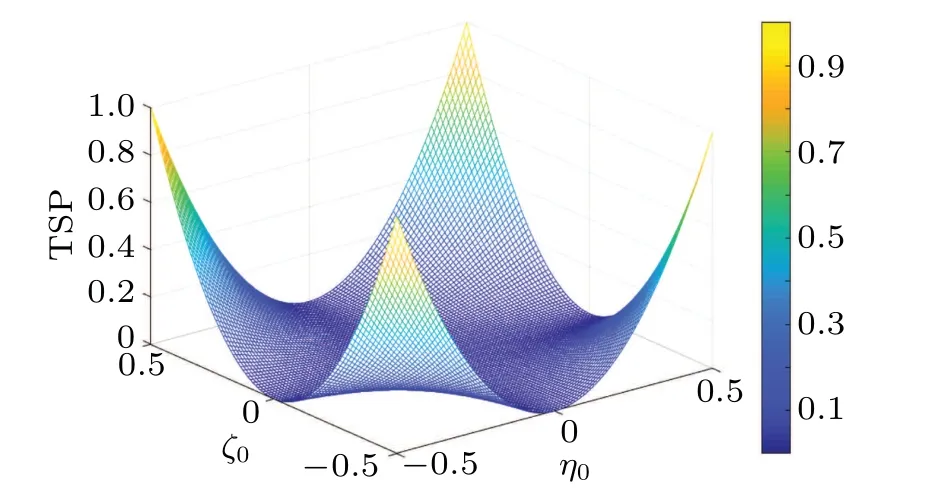
Fig.3.The relation among TSP and the parametersζ0 andη0 of channel entanglement.
For the second one,the total success probability(TSP2)can be expressed as

It is shown that the second scheme is deterministic.As different states can be synchronously obtained by the multiple receivers,its efficiency for qubits approaches the maximal value.
4.2.Communication efficiency and comparisons
Intrinsic efficiency[42]of remote state preparation schemes is defined as

where qpdenotes the number of prepared state,qcstands for the number of quantum channel and auxiliary particles,and the number of classical bits is expressed as xt.Applying Eq.(23),we compare the efficiencies of our proposed schemes with some other RSP schemes using non-maximally entangled channels in Table 3.
It is apparent that the intrinsic efficiencies of our schemes are highest among the others.Actually,the comparison of efficiency is only a part reflection of the actual situation.Our proposed schemes have several other nontrivial features:(1)the non-maximally entangled channels are easy to generate compared to maximally entangled states;(2)for the second scheme,the assistance of auxiliary particle is not required,whereas in some present schemes;[26,46–49](3)the success probability of the second scheme is independent of the channel parameters,and higher than the RSP protocols using nonmaximally entangled channels.[31,32,43]
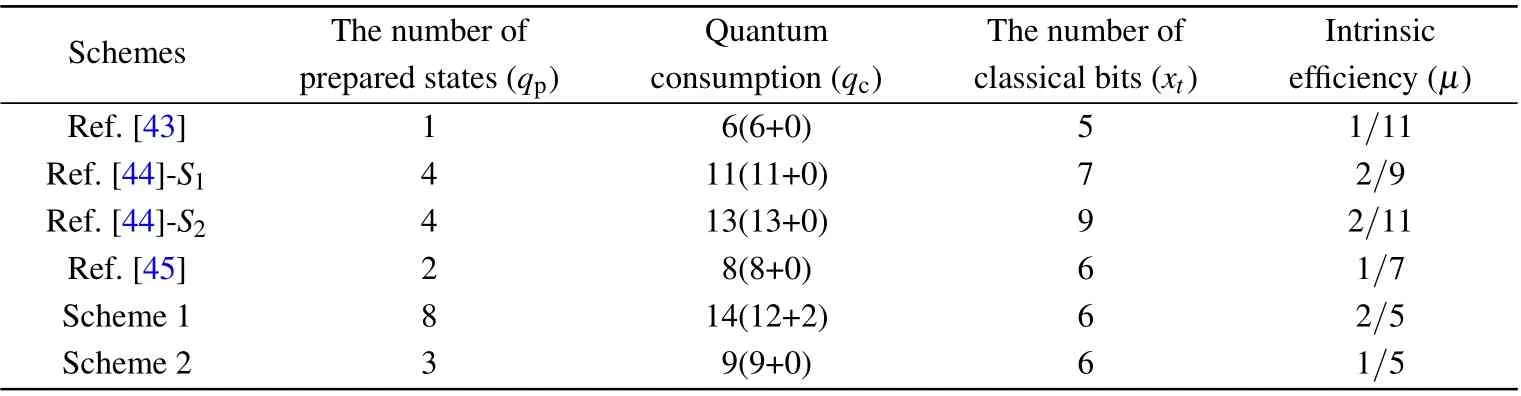
Table 3.Comparison with some other RSP schemes using non-maximally entangled channels.
5.Conclusions
In addition to the conventional RSP with two parties,multiparty RSP plays a significant role in the general quantum network communication and quantum distributed computation.Different from joint remote state preparation,our concern is to investigate the multicast-based RSP with one sender to multiple receivers taking non-maximally entangled state as the shared entangled resources.In particular,each receiver can obtain different quantum information synchronously.
To this aim,we put forward two three-party multicast schemes based on the non-maximally entangled channels,where sender Alice remotely help receivers Bob and Charlie prepare different quantum states synchronously.Firstly,sender and controller construct two sets of completely orthogonal bases.After their measurements,two receivers recover the states by unitary operations.In the first scheme,each receiver can obtain the different four-qubit cluster-type states probably,and its probability depends on the channel parameters(ζ0andη0).To improve the probabilities of such multicast RSP using the non-maximally entangled channel,by the nine-qubit partially entangled channel,the determined multicast CRSP scheme is given in the second scheme,so that Bob can obtain an arbitrary single-qubit state,and Charlie obtains an arbitrary two-qubit state synchronously.It is worth emphasizing that the probability of the second scheme can reach 100%,irrespective of liand ki,and auxiliary resources are not required.It is shown that the non-maximally entangled channels may offer some significant advantages in quantum information transmission.
杂志排行
Chinese Physics B的其它文章
- Multiple solutions and hysteresis in the flows driven by surface with antisymmetric velocity profile∗
- Magnetization relaxation of uniaxial anisotropic ferromagnetic particles with linear reaction dynamics driven by DC/AC magnetic field∗
- Influences of spin–orbit interaction on quantum speed limit and entanglement of spin qubits in coupled quantum dots
- Magnetic and electronic properties of two-dimensional metal-organic frameworks TM3(C2NH)12*
- Preparation of a two-state mixture of ultracold fermionic atoms with balanced population subject to the unstable magnetic field∗
- Quantum metrology with coherent superposition of two different coded channels∗
