Mobility edges and reentrant localization in one-dimensional dimerized non-Hermitian quasiperiodic lattice∗
2021-09-28XiangPingJiang蒋相平YiQiao乔艺andJunPengCao曹俊鹏
Xiang-Ping Jiang(蒋相平),Yi Qiao(乔艺),and Jun-Peng Cao(曹俊鹏),3,4
1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
3Songshan Lake Materials Laboratory,Dongguan 523808,China
4Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China
Keywords:Anderson localization,non-Hermitian quasiperiodic lattice,mobility edges
1.Introduction
Anderson localization is an important research topic in condensed matter physics and has been extensively studied since the pioneer work of Anderson.[1]The phenomenon of localization induced by random disorder depends crucially on the dimensionality.For example,it is found that any finite disorder can localize all single-particle states in one-or twodimensional noninteracting disordered systems.[2–4]In three dimension,the system can undergo a metal–insulator transition with the increase of disorder and forms a regime hosting both extended and localized states.The key feature of this hybrid regime is the existence of the mobility edges,which divide the states into extended or localized states by a critical energy.The quasiperiodic systems could display localization transitions at a finite quasiperiodic potential strength in one dimension.A typical quasiperiodic example is the Aubry–Andr´e–Harper(AAH)model,[5,6]which exhibits a self-dual symmetry and has an energy-independent localization transition,i.e.,all the states are completely extended(or localized)if the quasiperiodic potential strength is smaller(or greater)than the critical value.Therefore,mobility edges do not exist for the original AAH model.However,with the introduction of long-range hopping terms or modified quasiperiodic potentials,many generalized AAH models tends to have exact energy-dependent mobility edges.[7–12]These models with exact mobility edges are beneficial to provide a deeper understanding of Anderson localization in one-dimensional quasicrystals.
Recently,an important progress is that the onedimensional dimerized lattice with Hermitian staggered quasiperiodic potential can hold two localization transitions with the increase of disorder strength.[13]Generally,all the states remain localized after the localization transition.However,it is not always true in the one-dimensional dimerized quasiperiodic systems.In Ref.[13],the authors find that the competition between the dimerization and quasiperiodic disorder leads to a reentrant localization transition.The reentrant localization transition is defined as follows.After the first localization transition,some already localized states become extended for a range of intermediate disorder strength.With further increase of the quasiperiodic disorder strength,second localization transition arises where all the states become localized again.The reentrant localization transition is associated with intermediate phases hosting the mobility edges.This nontrivial reentrant localization can also be induced by the anisotropic dipole exchange in two-dimensional disordered dipolar quantum systems.[14]
In recent years,the Anderson localization and topological phase transitions in various non-Hermitian disordered systems have attracted a lot of attention.[15–27]In general,the non-Hermiticity comes from the nonreciprocal hopping processes or complex onsite potentials,which may induce exotic phenomena without Hermitian counterparts,such as the exceptional points,[28]PT symmetry breaking,[29]non-Hermitian skin effects,[30–32]as well as the fantastic dynamics and transport properties.[33–35]In the study of Hatano–Nelson model,[36,37]it is found that the asymmetric hopping introduced in one-dimensional Anderson model results in a localization-delocalization transition and the existence of mobility edges.Besides the researches on non-Hermitian Anderson models,the non-Hermitian extension of the AAH models have also been studied in the contexts.[15–21,38]It is shown that the localization transition is accompanied by a topological phase transition in the non-Hermitian AAH models.[15,17,20]The non-Hermitian generalized AAH models with exact mobility edges are also studied.[39–43]However,discussions of the non-Hermitian effect on the reentrant localization in onedimensional dimerized quasiperiodic systems are still absent.
In this paper,we study the mobility edges and the reentrant localization transitions in one-dimensional dimerized lattice with non-Hermitian either uniform or staggered quasiperiodic potentials.Based on the analysis of energy spectrum,inverse participation ratio(IPR)and normalized participation ratio(NPR),the phase diagrams of the system is obtained.For the non-Hermitian uniform quasiperiodic potentials,the results show that there exists an intermediate phase with mobility edges because of the competition between the dimerization and the quasiperiodic disorder.From the behavior of mobility edges induced by the non-Hermitian potentials and comparing it with the Hermitian case,we find that the present regime of extended phase is reduced while that of localized phase is enlarged,and the localization transition is accompanied by the PT symmetry breaking transition.For the non-Hermitian staggered quasiperiodic potentials,there exist multiple reentrant localization transitions in a range of disorder strength for some suitable dimerization and non-Hermitian parameters.With the model parameters presented here,the system has three intermediate phases where the localized states coexist with the extended states.Therefore,after the first reentrant of localization transition,subsequent reentrant arises with the further increase of non-Hermitian parameter.The transitions are associated with separate intermediate regimes hosting mobility edges,and the critical regimes of multiple reentrant localization transitions are achieved.The results also indicate that the non-Hermitian parameter can break the reentrant localization transitions if it is large enough.
The rest of the paper is organized as follows.In Section 2,the non-Hermitian extension of one-dimensional dimerized lattice with uniform or staggered quasiperiodic potentials is introduced.In Section 3,the mobility edges in the system with non-Hermitian uniform quasiperiodic disorder are calculated,and the phase diagram is obtained and analyzed.In Section 4,the localization properties of the dimerized lattice with non-Hermitian staggered quasiperiodic potentials are studied,and the multiple reentrant localization transitions are interpreted.The corresponding phase diagram is given.The main results are summarized in Section 5.
2.The model Hamiltonian
Considering a one-dimensional dimerized lattice with non-Hermitian on-site quasiperiodic potential,the model Hamiltonian reads
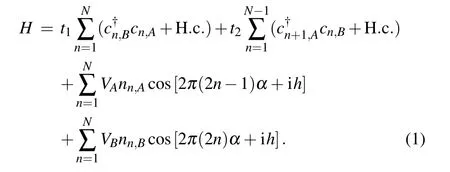

In order to study the localization properties of the eigenstates of model(1),we introduce two physical quantities:inverse participation ratio(IPR)and normalized participation ratio(NPR).[45,46]For the i-th eigenstateψi=(ψi1,ψi2,···,ψiL)Twhere T means the transpose,the IPR and NPR are defined as

Ifψiis localized,IPRiis finite and NPRiis proportional to 1/L which goes to zero at a limit of large L.Ifψiis extended,IPRi~1/L and NPRiis finite instead.These discussions indicate that IPRiis sensitive to the localized states while the inverse of NPRiis sensitive to the extended states.We further average these two quantities over all the eigenstates and obtain
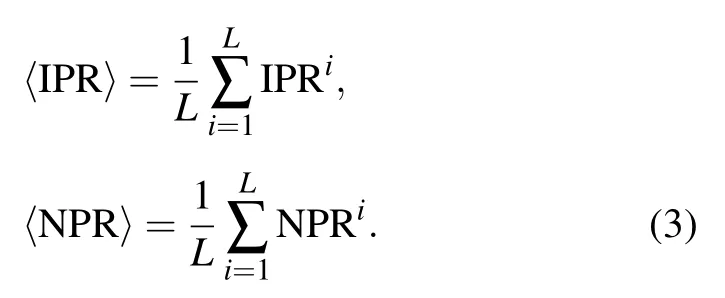
〈IPR〉and〈NPR〉carry complete information about the extended or localized properties of all the eigenstates of the system.If〈IPR〉~L−1and〈NPR〉is finite,the system is in the extended phase;If〈IPR〉is finite and〈NPR〉~L−1,the system is in the localized phase;If both〈IPR〉and〈NPR〉are finite,some eigenstates are extended and some are localized,which corresponds to the intermediate phase.
〈IPR〉and〈NPR〉can be combined as[13,46]

which helps distinguish intermediate phases from fully extended or localized phases clearly.This is because thatηis larger than−log10L in intermediate phases and smaller than−log10L in fully extended or localized phases.Now,we are ready to compute the non-Hermitian effects and phase diagrams of system(1).
3.Uniform quasiperiodic disorder
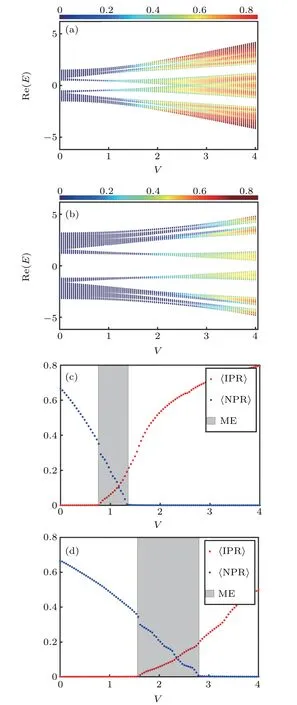
Fig.1.(a),(b)The real parts of energy spectrum Re(E)of the system with non-Hermitian uniform disorder versus the strength of quasiperiodic potential V withδ=0.5 and 2.2,respectively,where different colors denote different values of{IPRi}for each associated eigenstate.(c),(d)〈IPR〉(red dots)and〈NPR〉(blue dots)as the functions of V withδ=0.5 and 2.2,respectively.The shaded regimes are the intermediate phases with mobility edges.Here the non-Hermitian parameter is h=0.05.

Fig.2.The energy spectrum of the Hamiltonian(1)with non-Hermitian uniform quasiperiodic potential on the complex plane:(a)V=1.0,(b)V=2.0,and(c)V=3.0 for h=0.05,δ=2.2;(d)h=0.05,(e)h=0.125,and(f)h=0.2 for V=1.5,δ=2.2.
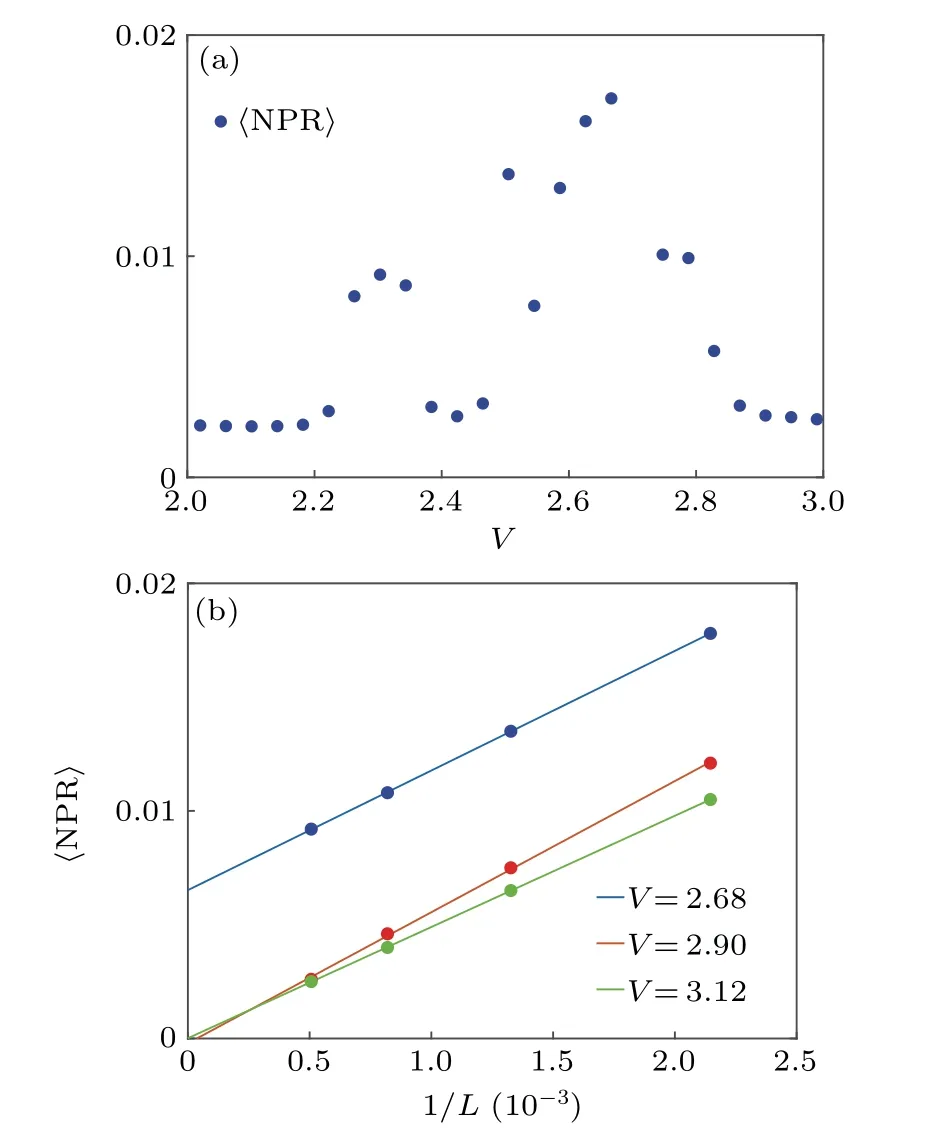
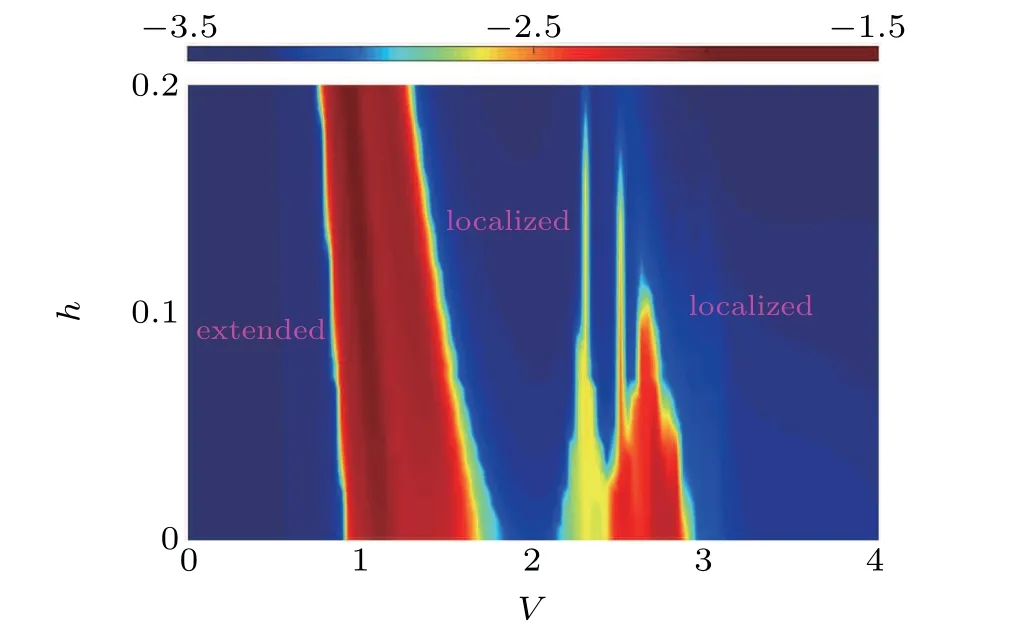
We first consider the system with non-Hermitian uniform quasiperiodic disorder,i.e.,VA=VB=V.In the limit of δ=1,model(1)reduces to the non-Hermitian extension of AAH model which exhibits localization transition without any mobility edges.Considering the general case and focusing on the non-Hermitian effects,we solve system(1)numerically.When the dimerization parameterδ=0.5,the real parts of energy spectrum versus the strength of quasiperiodic potentials V are shown in Fig.1(a),where different colors denote different values of{IPRi}for each associated eigenstate and the non-Hermitian parameter h=0.05.Localization transition and presence of the mobility edges can be easily seen from Fig.1(a),as well as that all the eigenstates are extended in weak disorder.With the increase of V,some eigenstates with real middle energy spectrum become localized,while the eigenstates with the edge energy spectrum keep extended.Thus the extended states coexist with the localized ones and the system has mobility edges.With the further increase of V,all the eigenstates are localized and the system enters into the localized phase.The resultant〈IPR〉and〈NPR〉are shown in Fig.1(c)as the red and blue dots,respectively.Therefore,there exists an intermediate phase with mobility edges where both〈IPR〉and〈NPR〉are finite(shaded regime for 0.76 The PT symmetry of system(1)can be broken by the disorder,as can be seen from the energy spectrum of the model with different disorder strengths shown in Fig.2.All the energies presented in Figs.2(a)and 2(d)are real,which means that the system is in the PT symmetric phase as well as the extended phase.However,from Figs.2(b)and 2(e),we find with the increase of disorder strength V and non-Hermitian parameter h,some energies become complex thus the system is in the PT symmetry-broken phase as well as the intermediate phase,which implies that there must be a PT phase transition at certain critical value of V or h.On further increasing V or h,it can be seen from Figs.2(c)and 2(f)that the eigenenergies are complex and the system is still in the PT symmetry-broken phase.However,this PT symmetry-broken phase is localized.Therefore,it can be stated that localization transition in the system is accompanied by the PT symmetry-breaking transition. Fig.3.Phase diagram of the system with non-Hermitian uniform disorder in V–h plane with dimerization parameterδ=2.2.Different colors indicate different values ofη.The dark blue regimes are extended phase and localized phase,while the dark red regime is the intermediate phase with mobility edges. Complete phase diagram of the system in V–h plane with δ=2.2 is obtained by the computation of quantityηgiven by Eq.(4).As shown in Fig.3,we find that system(1)has three different phases such as extended,intermediate,and localized phases.Note that all the eigenstates are extended in completely extended phase while localized in completely localized phase.The intermediate phase,where extended states coexist with localized states,has mobility edges.With the increase of non-Hermitian parameter h,the extended regime decreases while the localized regime increases.It is found that the localization transition arises readily in contrast with the Hermitian case. In this section,we focus on the mobility edges and reentrant localization in system(1)with non-Hermitian staggered quasiperiodic disorder,i.e.,VA=−VB=V.Figure 4 presents the real parts of energy spectrum,{IPRi}for each eigenstate,〈IPR〉and〈NPR〉versus different values of V with the model parameterδ=0.5 and 2.2.We first analyse the case of δ=0.5.It is seen from Figs.4(a)and 4(c)that there are two transition points V1=0.40 and V2=1.40 due to the competition between the dimerization and the staggered disorder.For weak disorder strength V The most interesting thing happens whenδis set as some suitable values.For example,whenδ=2.2 and h=0.05,the real part of energy spectrum is shown in Fig.4(b)and the corresponding〈IPR〉and〈NPR〉are shown in Fig.4(d).From Fig.4(d),we find that there is more than one localization transition with the increase of disorder strength V.For V<0.84,the energy spectrum is real and the system is in the extended phase.For 0.84 Fig.4.(a),(b)The real parts of energy spectrum Re(E)of the system with non-Hermitian staggered disorder versus the strength of quasiperiodic potential V withδ=0.5 and 2.2,respectively,where different colors denote different values of{IPRi}for each associated eigenstate.(c),(d)〈IPR〉(red dots)and〈NPR〉(blue dots)as the functions of V withδ=0.5 and 2.2,respectively.The shaded regimes are the intermediate phases with mobility edges.Here the non-Hermitian parameter is h=0.05. Then it can be concluded that there exist three localization transitions induced by the competition between the dimerization and staggered disorder.These reentrant localization transitions are associated with the intermediate phases hosting mobility edges.In the regimes of intermediate phases,i.e.,for 0.84 Fig.5.The energy spectrum of the Hamiltonian(1)with non-Hermitian staggered quasiperiodic potential on the complex plane:(a)V=0.5,(b)V=1.5,(c)V=2.0,(d)V=2.3,(e)V=2.6,(f)V=2.9.Here the model parameters are h=0.05 andδ=2.2. Fig.6.(a)The values of〈NPR〉for 2.0 In order to double check the above conclusion,the energy spectrum is calculated for specific values of disorder strength V in the regime of each phase,and the results are shown in Fig.5.It is clear that all results presented in Figs.5(a)–5(f)are consistent with those obtained from Fig.4(d). We should remark that the third intermediate regime is narrow and the corresponding values of〈NPR〉are small,and detailed values of〈NPR〉for 2.0 By the computation ofη,we obtain the phase diagram of the system in V–h plane shown in Fig.7.As can be seen from Fig.7,if the non-Hermitian parameter h=0,system(1)degenerates into the Hermitian version which has two stable intermediate phases.If h<0.025,there are two intermediate regimes and the system has reentrant localization.However,compared with the Hermitian case,the extended regime is smaller and localized regime is larger.If h=0.05,there exist three intermediate phases and the system undergoes three localization transitions.With the increase of h,the extended regime decreases while the localized regime increases.The behavior of first intermediate regime is similar to that of the system with non-Hermitian uniform quasiperiodic potential,while the other intermediate phases regimes gradually disappear.If h is large enough,only one intermediate phase will survive and there is no reentrant localization transition.Note that three intermediate phases and multiple reentrant localization transitions are missing in the Hermitian case. Fig.7.The phase diagram of the system with non-Hermitian staggered disorder in V–h plane with the dimerization parameterδ=2.2.Different colors indicate different values ofη.The dark blue regimes are extended or localized phases,while the remanent regimes are the intermediate phases with mobility edges. In this paper,we have studied the mobility edges and the localization transitions in one-dimensional dimerized lattice with non-Hermitian quasiperiodic disorders.In order to avoid perturbation of the boundary effects,we consider the system with periodic boundary condition.Based on the analysis of energy spectrum,〈IPR〉and〈NPR〉,we obtain the phase diagrams of the system,as shown in Figs.3 and 7. If the non-Hermitian quasiperiodic potentials are uniform,the system has three different phases such as extended,intermediate,and localized phases.We find that there is only one intermediate phase which has the mobility edges.With the increase of non-Hermitian parameter h,the extended regime decreases while the localized regime increases.Thus the localization transition arises more readily than the Hermitian case.It should be noted that the localization transition is accompanied by the PT symmetry-breaking transition. When the non-Hermitian quasiperiodic disorder potentials are staggered,we find that besides the extended and localized phases,the system also has three intermediate phases hosting mobility edges for certain values of non-Hermitian parameters.The behavior of first intermediate phase is similar to that of uniform case.Because the regimes of the second and third intermediate phases are small,based on the finite size scaling analysis,we demonstrate that these two phases indeed exist and the corresponding〈NPR〉/=0 at the thermodynamic limit with system size L→∞.The system undergoes three localization transitions through three intermediate phases.Note that these three localization transitions belong to the so-called multiple reentrant localization transitions demonstrated in the present non-Hermitian system.It should be remarked that the multiple reentrant localization transitions are stable and will arise within a finite interval of disorder strength V with suitable dimerization and non-Hermitian parameters.It is also found that the non-Hermitian parameter can break the reentrant localization transition,which is due to the fact that if h is large enough,only one intermediate phase survives and no reentrant localization transition arises.These results are quite different from those in the Hermitian case.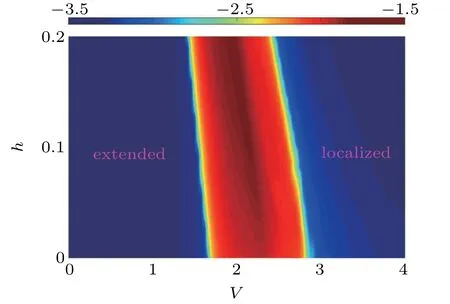
4.Staggered quasiperiodic disorder


5.Summary
杂志排行
Chinese Physics B的其它文章
- Multiple solutions and hysteresis in the flows driven by surface with antisymmetric velocity profile∗
- Magnetization relaxation of uniaxial anisotropic ferromagnetic particles with linear reaction dynamics driven by DC/AC magnetic field∗
- Influences of spin–orbit interaction on quantum speed limit and entanglement of spin qubits in coupled quantum dots
- Quantum multicast schemes of different quantum states via non-maximally entangled channels with multiparty involvement∗
- Magnetic and electronic properties of two-dimensional metal-organic frameworks TM3(C2NH)12*
- Preparation of a two-state mixture of ultracold fermionic atoms with balanced population subject to the unstable magnetic field∗
