Numerical simulation of anode heat transfer of nitrogen arc utilizing two-temperature chemical non-equilibrium model∗

Chong Niu(牛冲),Surong Sun(孙素蓉),Jianghong Sun(孙江宏),and Haixing Wang(王海兴)

School of Astronautics,Beihang University,Beijing 100191,China

Keywords:nitrogen arc,anode heat transfer,chemical non-equilibrium model,space charge sheath

1.Introduction

Understanding anode heat transfer is of great significance for the improvement of arc processing performance and extension of arc device lifetime.[1–6]Considerable studies of heat transfer between plasma and anode have been conducted for argon free-burning arc.[7–9]Compared with argon,nitrogen is a shielding gas with good protection,cheap cost and better energy source property,which is usually used in gas tungsten arc welding.[10,11]However,to our knowledge,there are few researches on the anode heat transfer of nitrogen arc both in experiments and numerical simulations.

At present the experimental measurements of nitrogen free-burning arc mainly focus on the temperature distributions and arc voltage characteristics.In Ref.[12],in order to avoid the anode ablation,a tungsten disc with 2%thorium oxide was used as the water-cooling anode to obtain the temperature distribution of nitrogen arc by the spectroscopic technology.[12]The laser-scattering measurement technology was adopted to get the temperature distributions of nitrogen arc without the local thermal equilibrium(LTE)assumption in Ref.[13].However,it is difficult to accurately measure the anode surface parameters such as temperature and heat flux distributions due to the steep parameters gradient,strong light emission,arc instability,etc.Therefore,the numerical simulation is required to investigate the plasma characteristics of nitrogen arc,especially the anode parameters distributions.

Compared with the numerical modeling of argon and helium arc,there have been few simulations of nitrogen freeburning arc.Most of the existing nitrogen arc models are based on the local thermal equilibrium(LTE)and local chemical equilibrium(LCE)assumptions without complete consideration of the space charge sheath.[10,14]However,the plasma near electrodes obviously deviates from LTE[15–17]and LCE,[18,19]thus the thermal and chemical non-equilibrium model is required to study the anode heat transfer of nitrogen arc.In our previous paper,[20]a thermal and chemical nonequilibrium model has been developed for nitrogen arc,but we did not focus on the anode heat transfer characteristics.Moreover,in the previous studies,[21,22]the space charge sheath can significantly affect the plasma energy flux and species flux on the anode surface.Therefore,the space charge sheath model should be included in the non-equilibrium model to accurately solve the species,current components,heat fluxes,and other parameters on the anode surface.

In this paper,a two-temperature chemical nonequilibrium model,coupled with collisionless space charge sheath model,has been developed for nitrogen arc.The numerical results are first compared with experimental data to validate the numerical model.Then the anode heat transfer of nitrogen arc is investigated utilizing this non-equilibrium model under different input current conditions and different anode materials.

2.Model description

In this section,the conservation equations and boundary conditions used in the non-equilibrium model are illustrated.

2.1.Assumptions

The calculation domain of the numerical model is shown in Fig.1.ABCDHG is the flow affected region,ABC is the cathode surface,and EFGH is the anode region.The radius of the cathode tip,i.e.,AB is 0.5 mm,and the cone angle of the cathode is 60°.The calculation domain is consistent with the structure of the experimental device in Ref.[12].

Fig.1.The computational domain for the numerical model.

The non-equilibrium model is developed on the basis of the following assumptions:(1)the arc is rotationally symmetrical operated with a non-ablating plane anode perpendicular to the arc axis.(2)Only self-induced magnetic field is included in the numerical model,i.e.,no external magnetic field.(3)The shielding gas is atmospheric pressure nitrogen and the gas flow is laminar.(4)Radiation loss is considered through net emission coefficient method.(5)Gravity and the effects of viscosity dissipation are negligible.(6)The electron and heavy-species temperatures are assumed in their own Maxwellian distributions.Therefore,the electron and heavyspecies energy equations are separately solved,and the energy exchange between electron and heavy-species is based on the elastic collision processes.

2.2.Species and chemical reactions considered

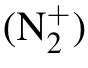
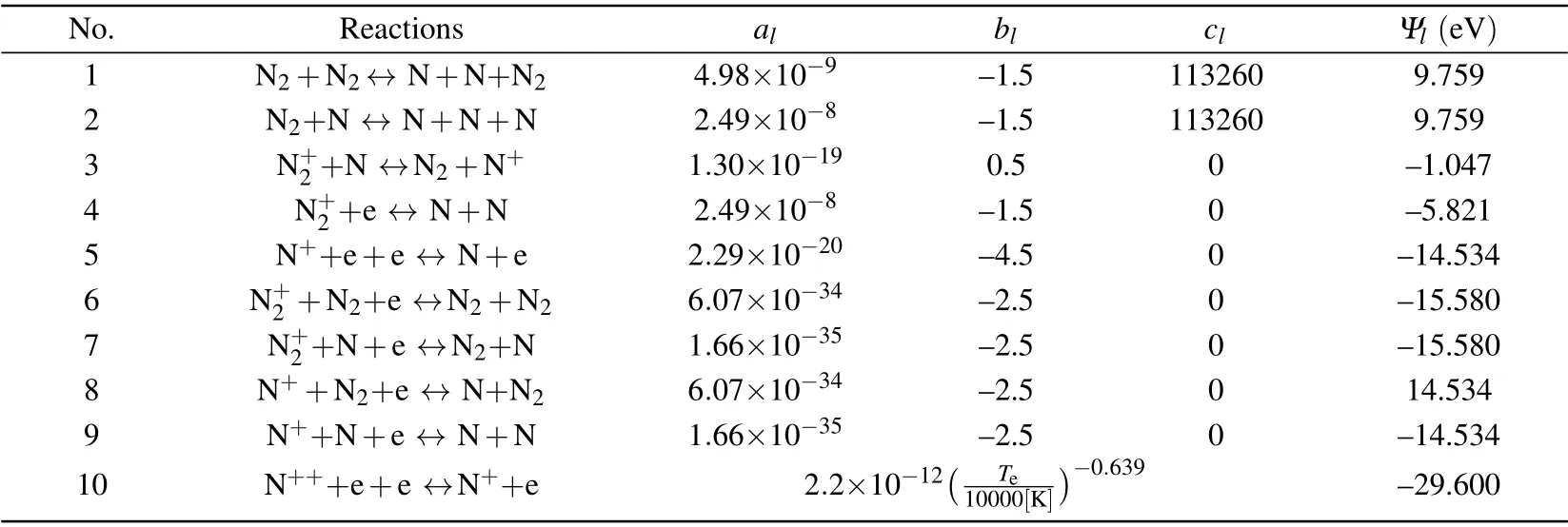
Table 1.The reactions taken in account in the numerical model.

2.3.Governing equations

Mass continuity equation

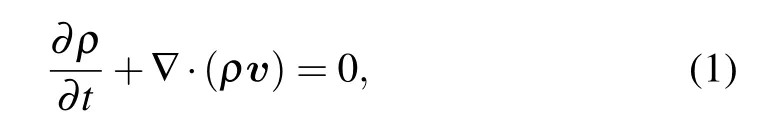
whereρis the mass density and v is the mass-averaged velocity.ρis calculated by the relationρ=∑inimi,where niand miare respectively the number density and mass for specie i.Momentum equation

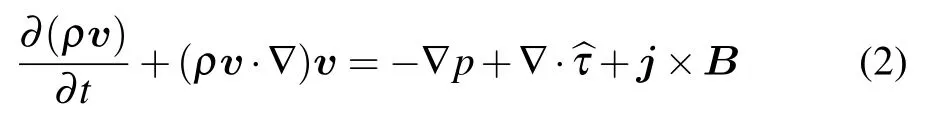
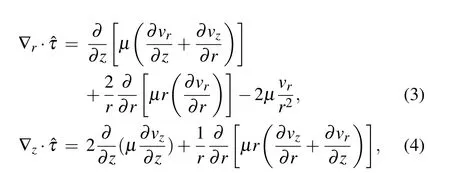
whereµis the viscosity of the shielding gas calculated by[27]

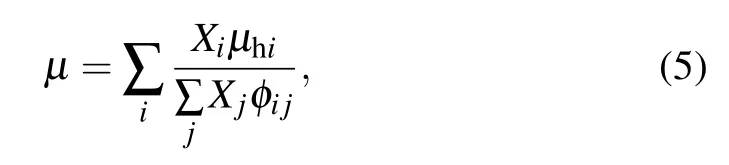
where Xiis the mole fraction of species i.φijis a dimensionless quantity calculated by the relation

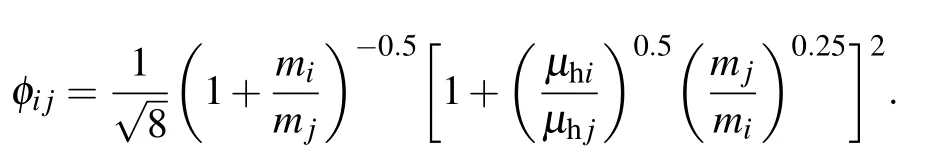
Theµhiis the viscosity of species i described as

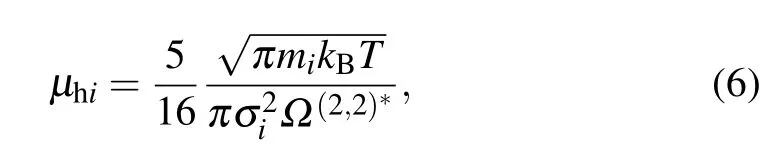
where kBrepresents the Boltzmann constant and T is the temperature of the corresponding species.σiis the collisional diameter andΩ(2,2)∗is the collisional integral.[28]

General species equation

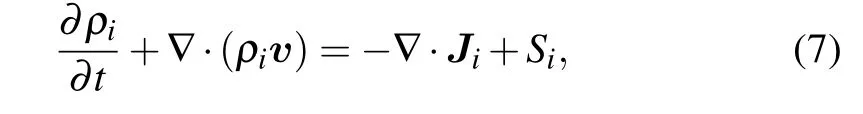
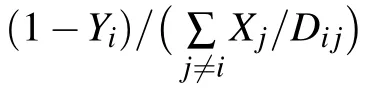
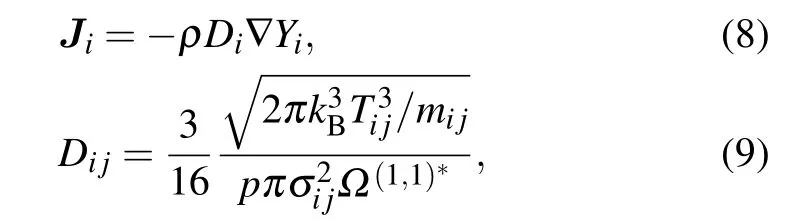
where Tijis the reduced temperature and mijis the reduced mass for the species i and j.For the ion equations,the ambipolar diffusion coefficient Damb,iinstead of Diis used to calculate the ion diffusive flux.[30]

Heavy-species energy equation

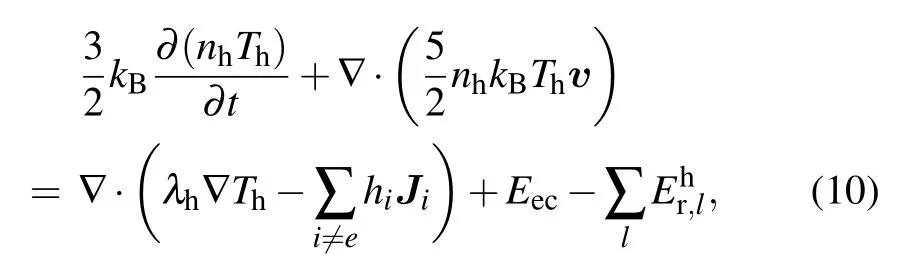
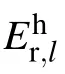
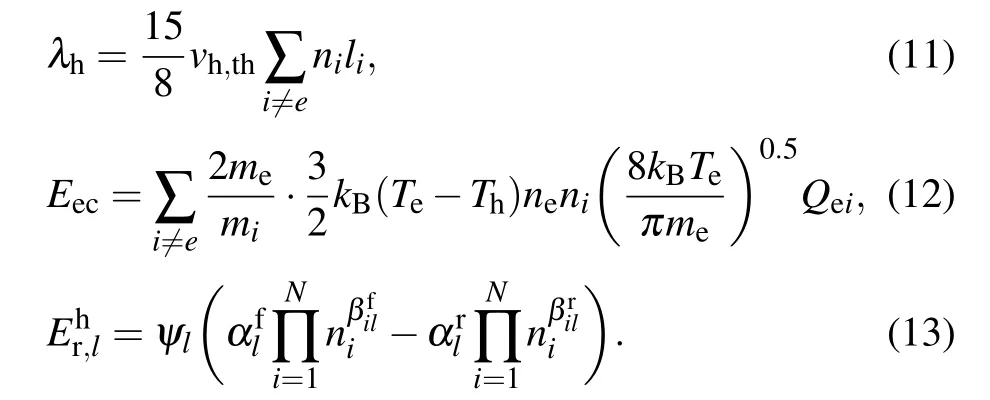
Electron energy equation

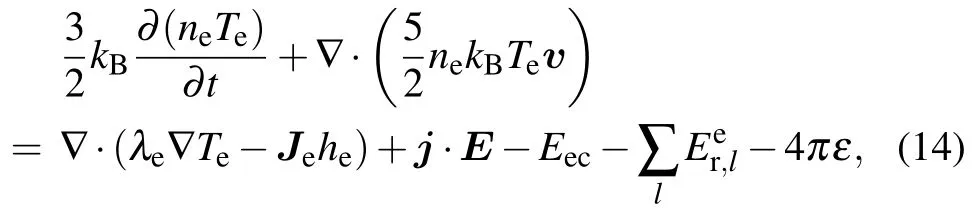
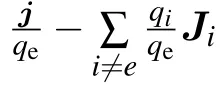
Current continuity,Ohm’s law,and Maxwell’s equation

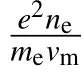
Heat transfer in solid

where Ts,ρs,Cps,λsandσsare the temperature,the mass density,the specific heat,the thermal conductivity and the electric conductivity of the solid anode,respectively.Two kinds of anodes made by copper and tungsten with thorium oxide are investigated,since these two anodes are often used in arc experimental devices.[12,32]The specific heat,electrical conductivity and thermal conductivity of anode materials are taken from Ref.[33].

2.4.Boundary conditions

The boundary conditions used in the model are listed in Table 2.Zero gradients of electron temperature and species density are set at the cathode surface,inlet and outlet.Dirichlet boundary conditions of heavy-species temperature and solid temperature are set on the boundaries except the anode surface(GH).For the velocity boundary conditions,no slip conditions are set on solid walls.Normal inflow velocity is defined on inlet to keep the flow rate and p=1 atm is set on the outlet.For the vector potential,zero gradient is given on electrode surfaces.The current density on boundary AB is set as a constant value with reference to Ref.[4],and on boundary BC it is set as the exponential distribution referring to Refs.[34,35].The anode bottom is connected to ground.The ions boundary condition in species conservation equation is−Jiw,a,and boundary conditions of neutral species are set as zero gradient on the anode.

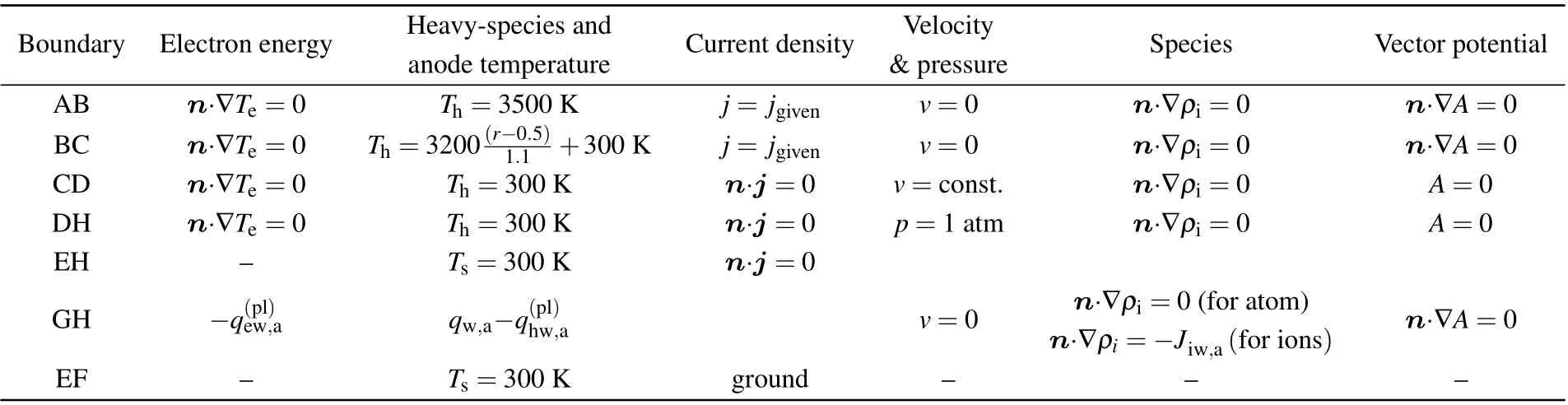
Table 2.The boundary conditions used in the numerical model.

The calculation domain includes the plasma flow affected region,pre-sheath and space charge sheath.In the twotemperature chemical non-equilibrium model,the pre-sheath,located in the near-anode region,is part of the plasma arc.Since the thickness of the space charge sheath is small,the space charge sheath can be treated as a zero-dimensional interface separating the plasma from the anode,and the appropriate boundary conditions are imposed to provide the sheath features.

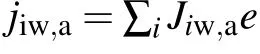
The heat flux on the anode surface is given as follows:

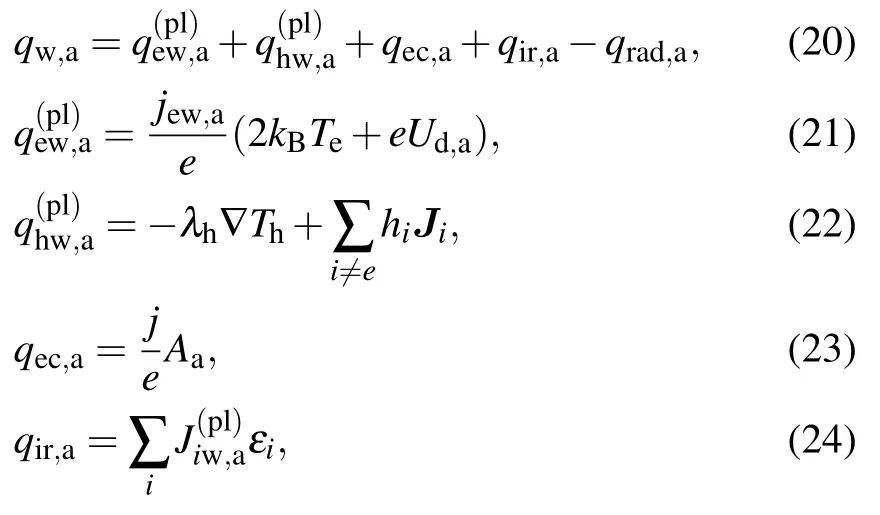
3.Results and discussion

3.1.Validation of the model

In order to validate our two-temperature chemical nonequilibrium model,the temperature distributions in plasma column are compared with the experimental measurement data of Haidar[12]and Murphy,[13]so the simulations are performed under the same working conditions as experimental measurements.The arc current is 200 A and the gas flow rate is set to 5 slpm.In the experiment the thoriated tungsten anode is adopted,which is cooled by direct contact with water and by conduction through the copper plate.[12]Figure 2 presents a comparison of our calculated temperature distribution with the spectroscopic measurement data.The lines are our numerical results and the dots are the measurement data obtained by Fowler–Milne method.It is seen that the isotherms of 24000 K,19000 K,14000 K and 9000 K agree well with the experimental measurement data,except for small difference occurring in the arc fringe.

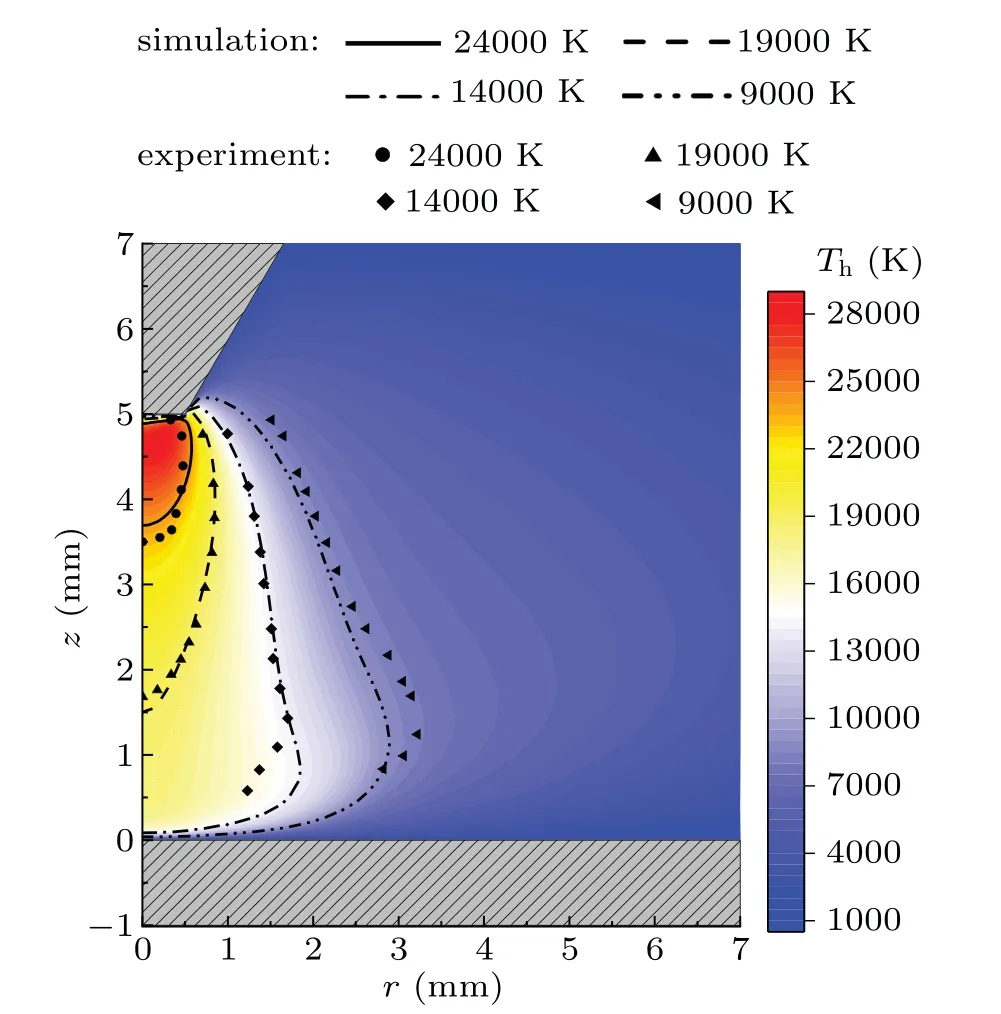
Fig.2.Temperature distribution of nitrogen plasma at 200 A arc current,the lines are the calculated heavy-species temperature and the dots are the measurement data taken from Ref.[12].

Figure 3 presents the radial distributions of our calculated electron temperature and experimentally measured temperature at different arc current conditions.The calculated temperature distributions are in reasonable agreement with the experimental data in the arc current range from 100 A to 300 A.The maximum temperature has an obvious rise when the arc current increases from 100 A to 200 A,while the plasma temperature increases slowly in the arc currents of 200 A to 300 A.The variation trend of temperature distributions with arc current is consistent with the experimental results in Ref.[12].

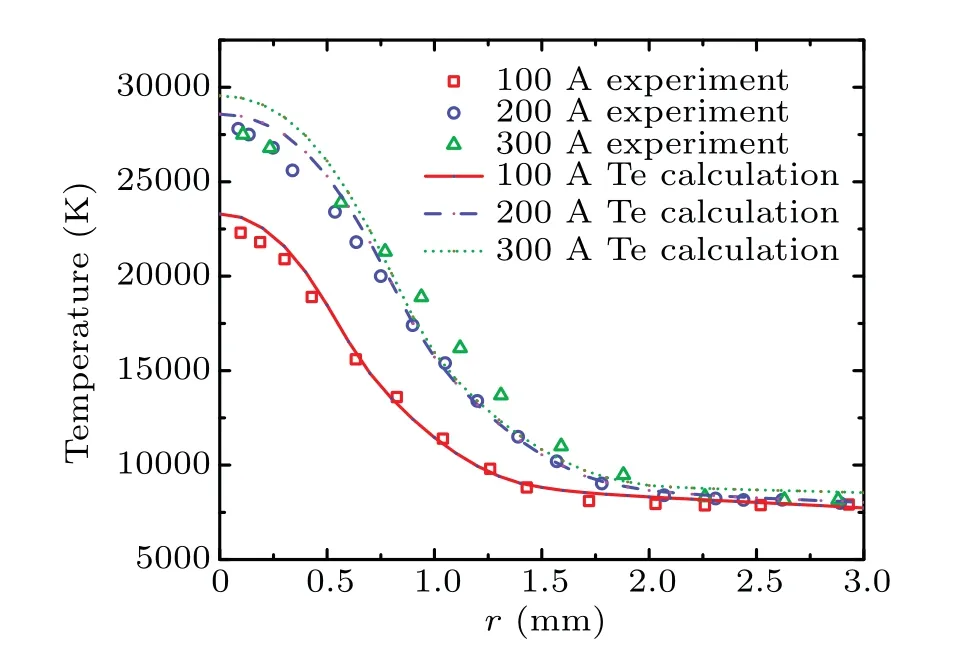
Fig.3.Radial distribution of calculated temperature and experimentally measured data for different arc currents at an axial distance of 4.5 mm from anode surface.

Figure 4 further shows the comparison of electron and heavy-species temperatures of numerical model with the experimental data of Murphy[13]at different axial and radial positions.The symbols are experimental data measured by laser-scattering technique without the local thermal equilibrium assumption.[13]As shown in Fig.4,the numerical results agree well with the experimental data in the arc center.However,in the arc fringe region,where the temperature is below 5000 K,the electron temperature and heavy-species temperature deviate from the measured data,especially for the temperature at the distances away from the anode.The discrepancy at the arc fringe may be caused by the chemical nonequilibrium processes.In general,these comparisons indicate that our present model can reasonably predict the temperature distributions of nitrogen arc.

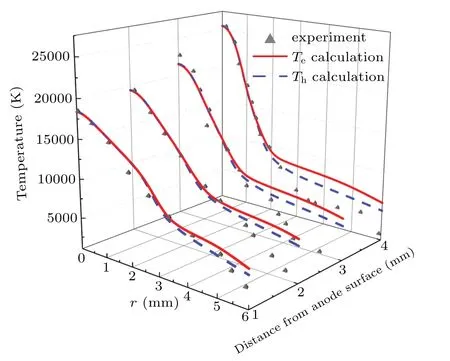
Fig.4.Comparison of calculated electron and heavy-species temperatures with experimental data[13]at different axial and radial positions.

Fig.5.Radial distribution of anode heat flux calculated by different numerical models at 150 A arc current.

Since we focus on the heat flux distribution on the anode surface,figure 5 exhibits the radial distribution of heat flux on copper anode surface at 150 A arc current.The anode heat flux calculated by Tanaka is based on the thermal and chemical equilibrium model.[14]The total heat flux in Ref.[14]includes the heat conduction flux from plasmas and electron condensation heat.The anode heat flux in our model includes electron condensation heat,heat flux from heavy-species and electrons through conduction and enthalpy transport,ion recombination heat flux and radiation loss,which is calculated by thermal and chemical non-equilibrium model considering the collisionless space charge sheath.On the arc axis,the anode heat flux calculated by our non-equilibrium model is a little higher than that calculated by the equilibrium model.This may be due to the inclusion of more anode heat flux components in our model,such as heat released by ion recombination,which was ignored in Ref.[14].In the arc fringe,there is a difference between the anode heat fluxes calculated by the two sets of numerical models.This discrepancy may be related to the effect of non-equilibrium characteristics.

Fig.6.Temperature distribution of nitrogen arc plasma at 100 A(a),150 A(b),and 200 A(c)arc currents.

3.2.Arc current effects on anode heat transfer

The influence of arc current on the heat transfer of thoriated tungsten anode is investigated in this section,in which the gas flow rate is fixed as 5 slpm.Figure 6 shows the temperature distribution of nitrogen arc plasma column at 100 A,150 A and 200 A arc currents.The arc column shape is a typical bell-shape and the arc-anode attachment mode is diffuse.Enlargement of arc column is observed as the arc current increases from 100 A to 200 A.The maximum temperatures are respectively 25466 K,26853 K and 28528 K for 100 A,150 A and 200 A arc currents.Similarly,the temperature on the anode surface significantly rises with the arc current as shown in Fig.7.The maximum temperatures on the anode surface are respectively 1350 K,1900 K and 2450 K for the arc currents of 100 A,150 A and 200 A.All temperatures are lower than the melting point of thoriated tungsten anode,which indicates that the non-ablating anode assumption is reasonable in these working conditions.

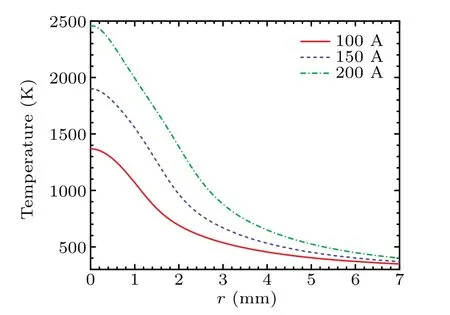
Fig.7.Radial distribution of current density on thoriated tungsten anode surface at different arc currents.

Figure 8 shows the radial distribution of current density on thoriated tungsten anode surface at different arc currents.Contrary to the variation trend of temperature on the anode surface,the maximum current density slightly decreases as the arc current increases.The‘arc radius’is defined in order to clarify the changing trend of current density.It is defined as the radius that includes 90%of total arc current on the anode surface,which was also used in Ref.[37]to characterize the arc constriction.On the anode surface,the arc radii are respectively 1.76 mm,1.90 mm and 2.29 mm for 100 A,150 A and 200 A current conditions,which indicates that the arc anode attachment area becomes more diffuse with the increase of the arc current.This phenomenon is consistent with the enlargement of plasma arc column upon increasing the arc current.Hence,the decrease of the maximum current density on the arc axis is caused by the arc expansion.

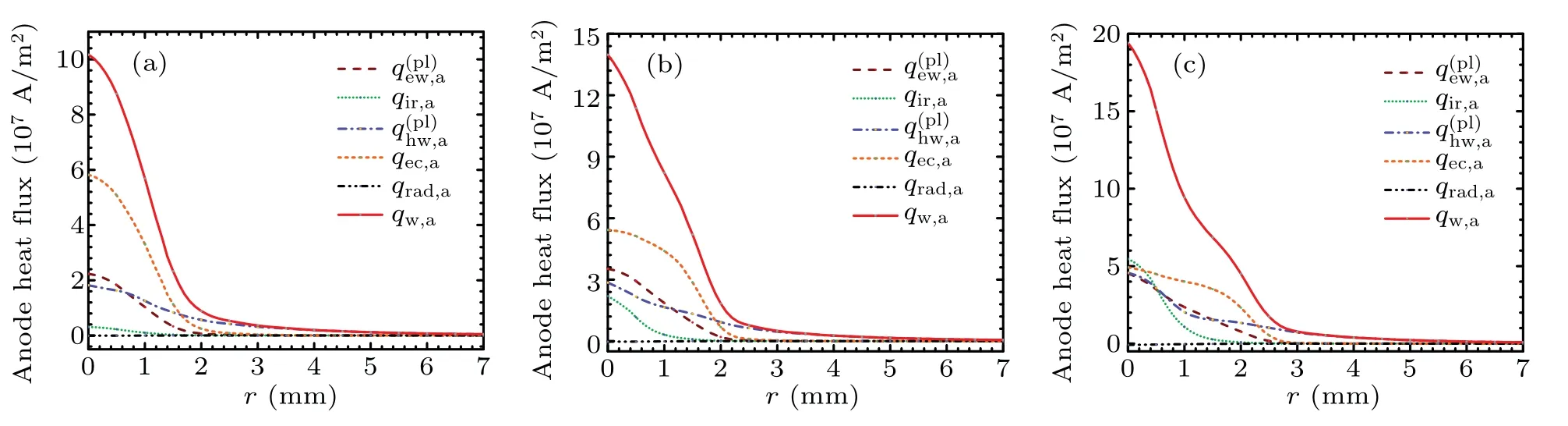
Fig.9.Radial distribution of anode heat flux on thoriated tungsten anode surface at arc currents of 100 A(a),150 A(b),and 200 A(c).

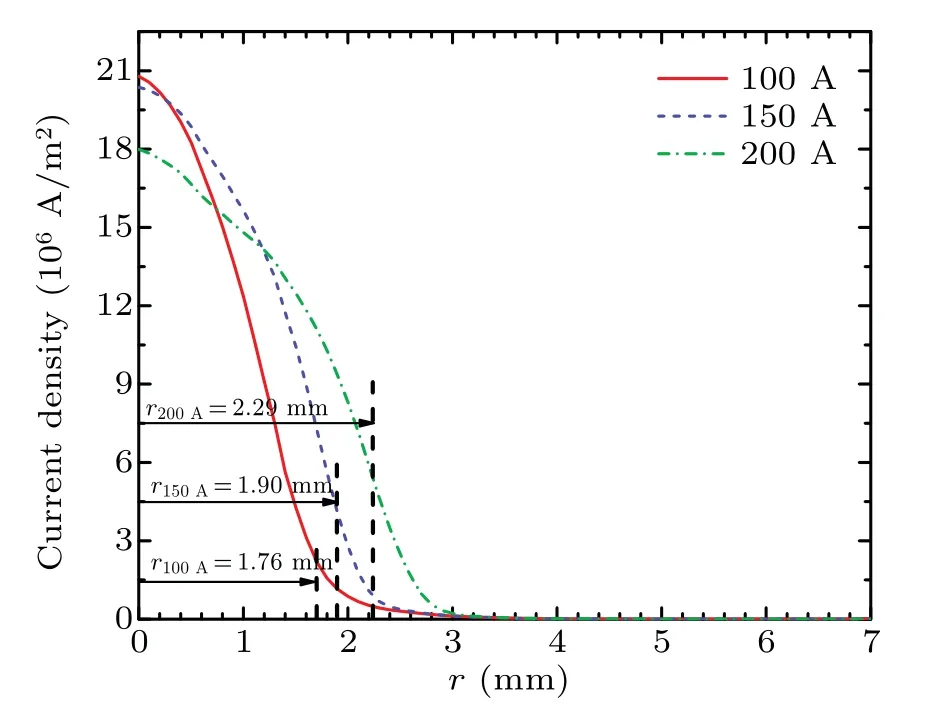
Fig.8.Radial distribution of current density on thoriated tungsten anode surface at different arc currents.

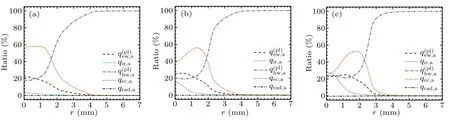
Fig.10.Radial distribution of the ratio of different heat flux components on thoriated tungsten anode surface at arc currents of 100 A(a),150 A(b),and 200 A(c).

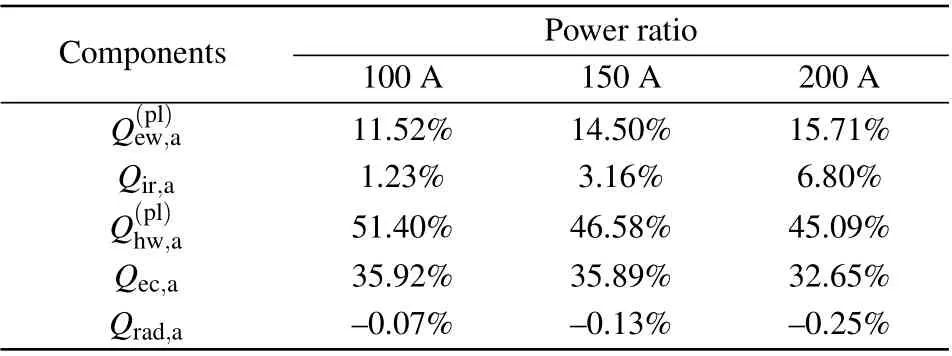
Table 3.Radial distribution of temperature on thoriated tungsten anode surface at different arc currents.

3.3.Material effects on anode heat transfer

Reasonable selection of electrode materials is of importance to extend the lifetime of arc device.Therefore,the effects of materials on the anode heat transfer are investigated in this section.The tungsten doped with thorium is often adopted as the anode material of nitrogen arc device.[12,13]On the other hand,the copper anode is also widely applied in the transferred and non-transferred arc devices.[32]Thus in this study the copper anode and thoriated tungsten anode are selected to investigate the material effects on anode heat transfer.

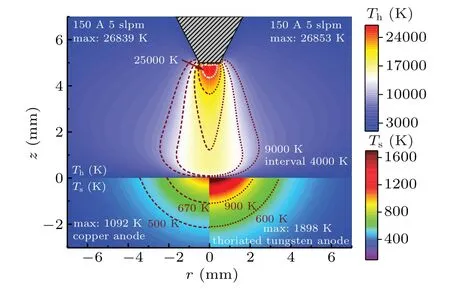
Fig.11.Temperature distributions of nitrogen arc at 150 A arc current for different anode materials.

Figure 11 presents the temperature distributions of nitrogen plasma at 150 A arc current for different anode materials.It can be seen that the temperature differences in plasma arc column are negligible for the copper anode and thoriated tungsten anode.Both the arc profile and the maximum temperature are almost the same for the copper anode and thoriated tungsten anode.Although there is almost no difference in the temperature of arc column,the temperature in the anode region is obviously different.The maximum temperature is 1092 K on the copper anode surface,which is about 800 K lower than the maximum temperature on thoriated tungsten anode surface.Moreover,the temperature gradient is steeper in the thoriated tungsten anode due to lower thermal conductivity,leading to a higher maximum temperature in the thoriated tungsten anode.Therefore,these results indicate that anode materials have a significant influence on temperature distribution in the anode region,while the temperature of plasma column is hardly affected by anode materials in the case of non-ablating anode.

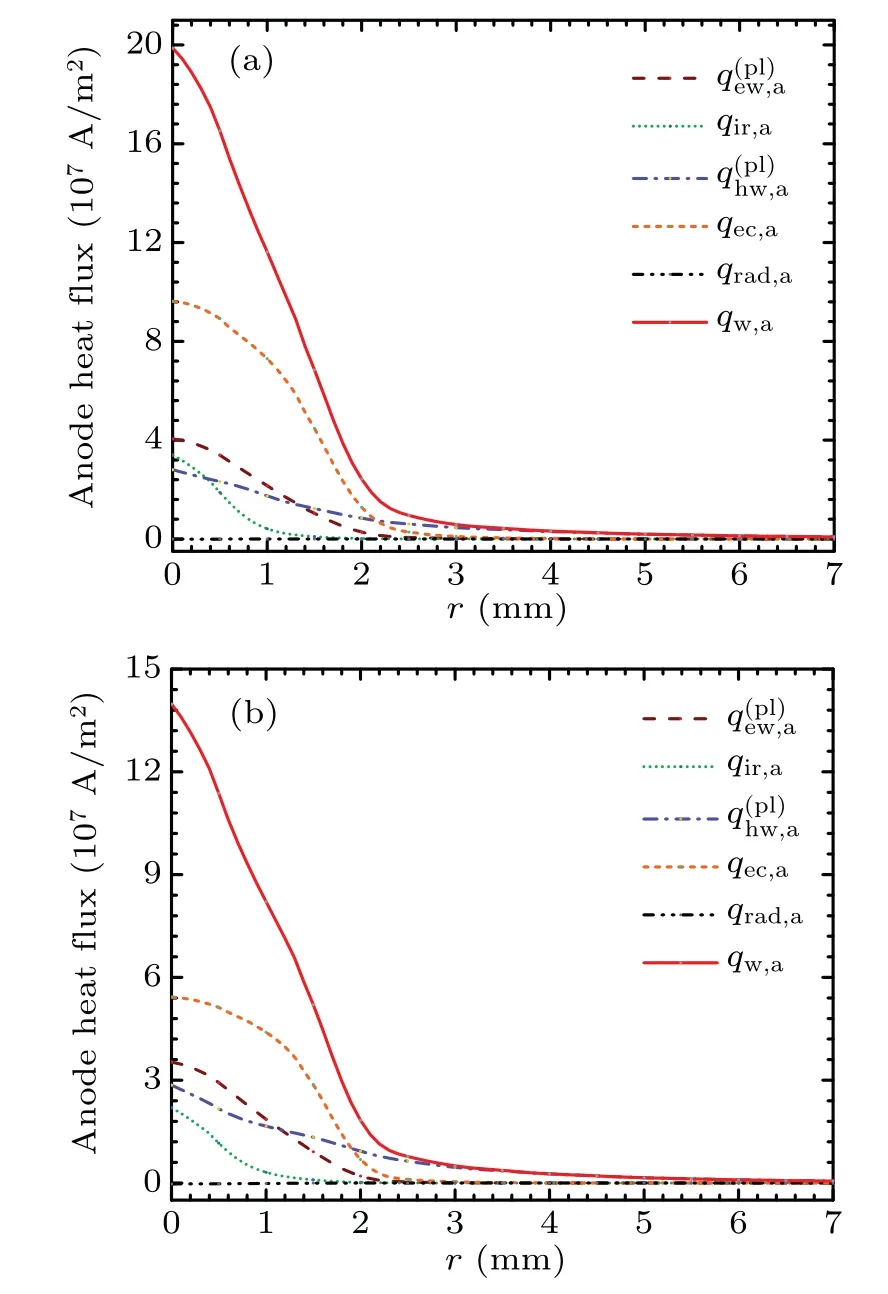
Fig.12.Radial distribution of heat flux on copper anode surface(a)and thoriated tungsten anode surface(b)at 150 A arc current.

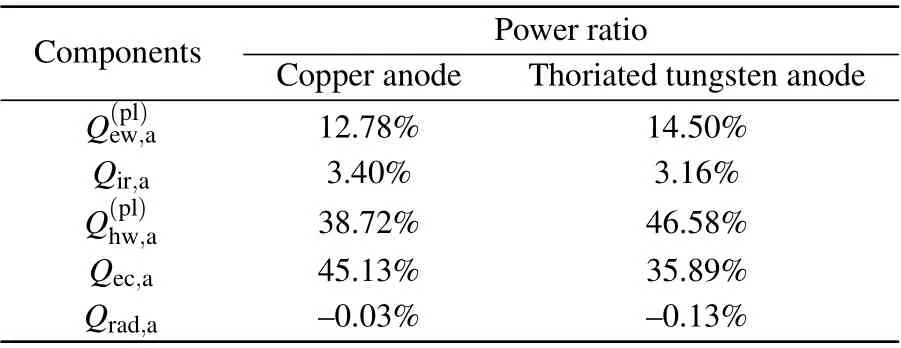
Table 4.The ratio of power transferred to the anode through each heatflux component at 150 A arc current.

4.Conclusions

The two-temperature chemical non-equilibrium model is adopted to investigate the anode heat transfer of nitrogen arc in this paper.The interactions of plasma arc with the anode are considered in detail by including the collisionless space charge sheath.The electron and heavy-species temperature distributions are compared with the experimental data to validate our model.Moreover,the total anode heat flux calculated by our non-equilibrium model is compared with that of equilibrium model of Tanaka.Then we use the two-temperature chemical non-equilibrium model to study the effects of different arc currents and anode materials on the anode heat transfer.

The results indicate that the arc current affects the temperature and heat flux distribution of anode region by changing the plasma characteristics distributions in the arc column.As the arc current increases from 100 A to 200 A,the plasma arc column enlarges,resulting in the more diffuse arc anode attachment region.Therefore,the maximum electron condensation heat flux decreases with the increase of arc current,while the maximum heat fluxes from plasma electrons and heavyspecies and ion recombination heat increase.It is found that the electron condensation heat flux,the heat flux from plasma electrons and ion recombination heat flux are mainly concentrated in the high current density region.The heat flux from heavy-species decays slowly in the radial direction,becoming the main heat flux component in the arc fringe.The power transferred to the anode by each heat flux component is obtained.The contribution of each heat flux component to power transferred to anode changes slightly in the current range from 100 A to 200 A.The heat flux from plasma heavy-species and the electron condensation heat are the first and second contributions to power transferred to the thoriated tungsten anode.

The anode material hardly affects the temperature distribution of plasma arc column,while it has a significant effect on the temperature and heat flux distributions in the anode region.The total heat flux on copper anode is higher than that on thoriated tungsten anode,and this difference is mainly caused by electron condensation heat.However,the maximum temperature on copper anode is lower than that on thoriated tungsten anode.This phenomenon is caused by a steeper temperature gradient in the thoriated tungsten anode region due to the lower heat conductivity.For the copper anode,the maximum contribution to power transferred to anode is electron condensation heat,which is different from that of thoriated tungsten anode.The electron condensation heat instead of heat flux from plasma heavy-species makes the largest contribution to power transferred to anode due to the high work function of copper.