Unstable mode of ion-acoustic waves with two temperature q-nonextensive distributed electrons
2021-09-28BukhariNadeemHussainandAli
S Bukhari,Nadeem Hussain,and S Ali,2
1Department of Physics,The University of Azad Jammu and Kashmir,Muzaffarabad 13100,Azad Kashmir,Pakistan
2National Center for Physics at QAU Campus,Shahdra Valley Road,Islamabad 44000,Pakistan
Keywords:non-gyrotropic,nonextensivity,Saturns’s magnetosphere
1.Introduction
Plasma physics deals with a rich variety of linear and nonlinear structures and modes.Acoustic-like modes are energy propagation through a medium exhibiting an adiabatic compression and decompression.In this article,we restrict ourselves on the discussion of low frequency ion-acoustic waves amongst various other plasma modes.These waves were theoretically predicted by Tonks and Langmuir[1]while verified experimentally by Revans.[2]Moreover,their Landau damping was first measured in cesium and potassium by Wong,Motley and D’Angelo.[3]An ion-acoustic wave can propagate both in magnetized and unmagnetized plasmas under the constraints vTi≪ω/k≪vTe,where vTiand vTeare the thermal speeds of ions and electrons,respectively,whileω/k shows phase speed of the wave.These waves have wide range of practical applications in classical,quantum,semiconductor,relativistic,nonrelativistic,and gaseous regimes of the laboratory and space plasmas.
Many authors investigated the linear and nonlinear characteristics of the ion-acoustic waves by considering various conditions and models in electron-ion Maxwellian plasmas.[4–7]The investigations of the ion-acoustic waves were carried out[8–10]on the basis of collisionless Boltzmann equation and found that these waves exhibit strong Landau damping when both electrons and ions are at the same temperature.The collisional effects produced due to the mutual interactions of ions were examined by Bhadra and Varma.[11]Furthermore,the role of Coulomb collisions in the damping of ion-acoustic waves was investigated by Buti,[12]who identified that such a type of collisions are responsible for the enhancement of damping.
Most frequently,the studies were carried out by assuming a single component of electron.However,a few investigations were found[13–15]with the existence of two components of electrons with different temperatures,referred to as hot and cold electrons in both space plasmas[16,17]and laboratory.[18,19]Sittler,Ogilvie and Scudder[20]predicted the presence of hot and cold electron components in Saturn’s magnetosphere during the Voyager PLS observations and later confirmed by Young et al.[21]with the cassini plasma spectrometer(CAPS)observations.The characteristics of ion-acoustic waves are significantly modified in the presence of two distinct components of electrons.[22]The investigation of nonlinear propagation of coupled Langmuir and ion-acoustic waves was carried out[23]in a two-temperature electron plasma.The study revealed the coupled Langmuir ion-acoustic solitons propagating with the supersonic speed.Kourakis and Shukla[24]studied the dispersive properties of ion-acoustic waves in two-temperature electrons plasma and examined the envelope excitations and oblique modulation.They found that satellite observations are in good agreement with the localized excitations concerning the magnetosphere environment.The Voyager observations of Barbosa and Kurth[25]revealed the nonthermal nature of electron velocity distributions in the outer region of Saturn magnetosphere.
Many theoretical and experimental studies showed that Boltzmann–Gibbs(BG)statistics is inappropriate for description of nonextensive systems,i.e.the systems exhibiting long range interactions.Due to this discrepancy of the BG statistics,Tsallis[26]presented a new idea of the Tsallis statistics by incorporating all the necessary informations of nonextensive phenomenon which has attracted a considerable attention of many researchers.[27–34]Recent literature shows an increasing interest of investigating the plasma dynamics with a new and more generalized statistical approach,i.e.,qnonextensive statistics.Identification of nonthermal particles in various environments of space plasmas has been verified by many spacecraft measurements.[35–37]The generalized qdistribution has best fits for the magnetosheath electron data observed from the AMPTE satellite and solar wind data obtained by CLUSTER.Several evidences showed the appropriateness of the nonextensive statistics for effective modelling of many physical systems,e.g.,the turbulent systems,[38]the plasma systems,[39,40]and the galaxy clusters.[41]The most significant property of the Tsallis statistics is pseudoadditivity,which shows that the total Tsallis entropy[26]of a system Sq(X+Y)composed of two independent subsystems X and Y satisfies Sq(X+Y)=Sq(X)+Sq(Y)+(1−q)Sq(X)Sq(Y).The total entropy Sq(X+Y)of a system is less than the sum of the entropies of individual subsystems if q<1,while it is greater than the sum of the entropies of subsystems for q>1.It is interesting to note that the Tsallis entropy reduces to the well-known Boltzmann–Gibbs entropy SBG=−kB∑ipiln piin the limit q→1,so that the standard additivity property of the entropy is retrieved.The statistical interpretation of the nonextensive system leads to the nonextensive q-distribution function for the particles.This distribution is the most generalized form of the particles distribution,as one can easily retrieve a Maxwellian distribution function from it in the limit q→1.Keeping in view of the generality of nonextensive qdistribution function and its relevance to the observed situation of Saturn’s magnetosphere,we choose this distribution in our present research work.Nonextensive statistics has various applications in the investigation of plasma waves and instabilities,such as the relativistic Langmuir waves,[42]the plasma oscillations,[43]Jeans instability,[44]the linear and nonlinear Landau damping rates.[45]Liu et al.[46]examined the currentdriven instability of ion-acoustic waves with nonextensive approach.The authors in their study assumed only one species of electrons with dynamical ions and showed that nonextensivity is not significant when electron temperature is much greater than the ion temperature.However,investigation of unstable mode of ion-acoustic waves having two distinct species of electrons,i.e.hot and cold electrons with nonextensive effects is quite interesting.
In the present work,we employ kinetic theory to investigate the unstable mode of ion-acoustic waves in a collisionless and magnetic-field free plasma,modelled by the nonextensive q-distribution function.The ion-acoustic waves can be excited to become unstable due to nonthermal equilibrium features of the plasma components where the velocity distribution function fα(vα)deviates from being a monotonically decreasing function of square of the velocity,i.e.,v2α.The source of free energy required for the excitation of ion-acoustic waves is provided by the relative directed motion of streaming hot electrons with respect to the other plasma species.A wellknown set of Vlasov–Poisson’s equations is used for the investigation of wave dynamics.The necessary condition for unstable waves is obtained showing the threshold limit,above which ion-acoustic wave becomes unstable.The dispersive characteristics of ion-acoustic waves and associated instability growth rate is analyzed both analytically and numerically.The graphical discussion is presented in Section 3 followed by summary of the work.
2.Basic description and mathematical formulation
We consider an electrostatic and collisionless plasma consisting of two distinct species of electrons,i.e.,streaming hot electrons and non-streaming cold electrons along with dynamical positive ions.The distribution of the plasma species is described by nonextensive q-distribution function.The plasma under consideration exhibits following charge neutrality condition,ni0=nh0+nc0,where ni0,nh0and nc0are the number densities of dynamical ions,hot electrons and cold electrons,respectively.The dynamics of ion-acoustic waves with two components of electrons can be examined by the well-known Vlasov equation

where fα1(r,vα,t)represents the perturbed distribution function and Qα(mα)is the charge(mass)ofαthspecies with α=h for hot electrons,α=c for cold electrons andα=i for dynamical ions.For convenience,the electric field can be expressed in terms of electrostatic potential,i.e.,E1=−∇V1.Equation(1)must be coupled together with Poisson’s equation for complete description of electrostatic ion-acoustic waves.The linearized form of Poisson’s equation is expressed as
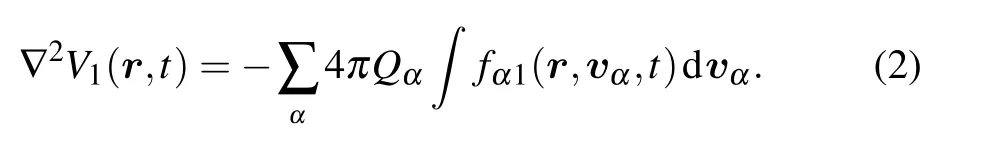
Adopting the standard procedure of kinetic theory,Eqs.(1)and(2)can be solved by eliminating fα1to finally arrive at the generalized dielectric response function[47]in a collisionless unmagnetized plasma,as


The modified plasma dispersion function(6)can be expanded into asymptotic series by considering small and large arguments.For small arguments,i.e.,ξα=ω/kvTα≪1,Zq(ξα)can be approximated[51]as

and for large arguments,i.e.,ξα≫1,we have

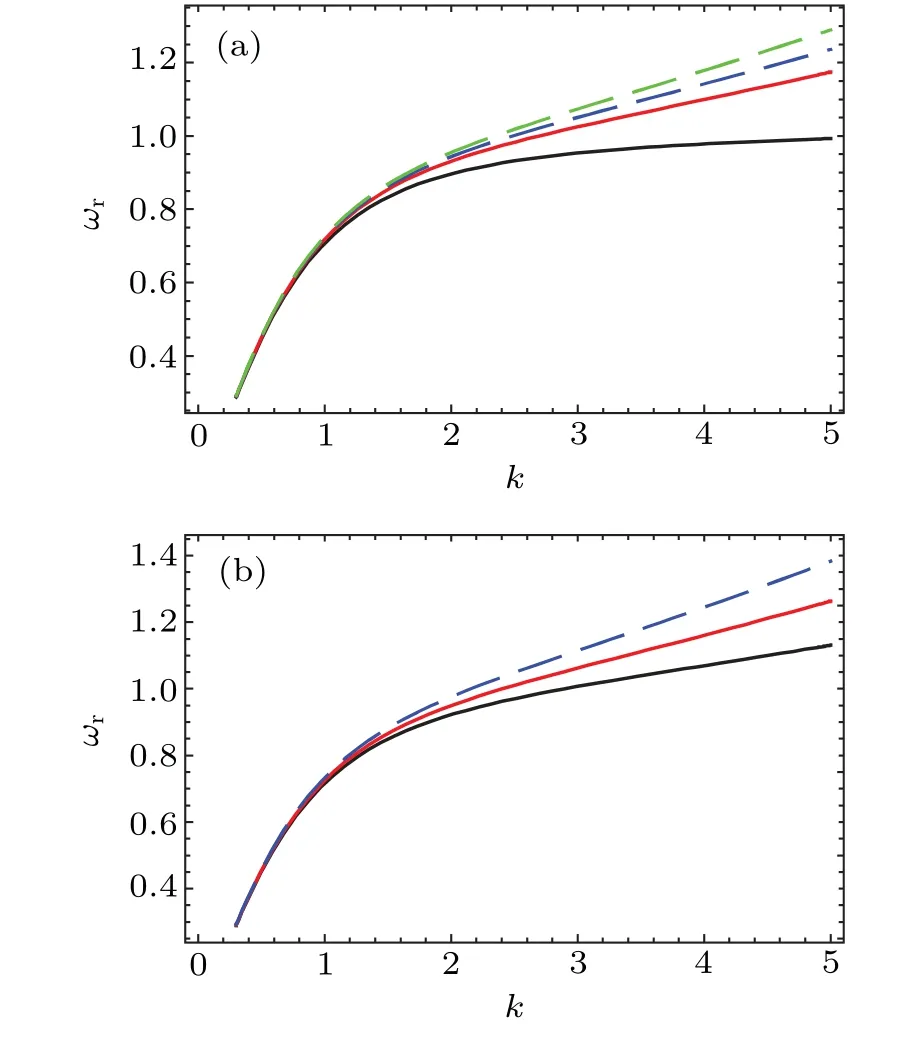
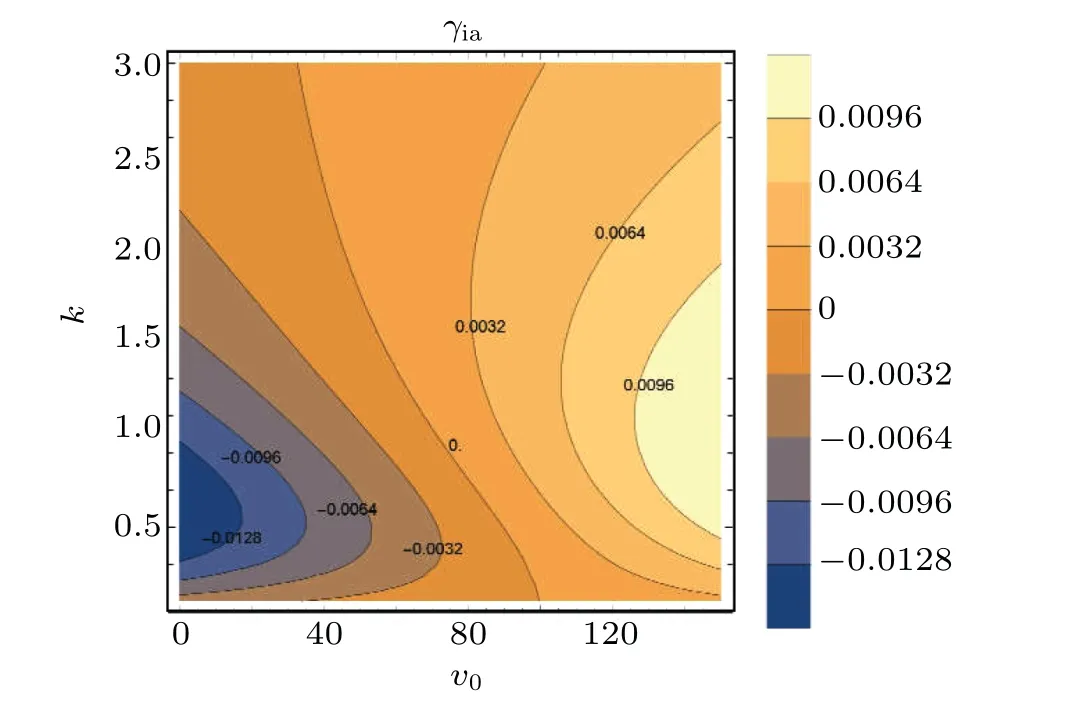
For ion-acoustic waves,the phase speed constraints in comparison with thermal speeds lead to vTi≪ω/k where the susceptibilities of hot electrons,cold electrons and dynamical ions are,respectively,defined as It is seen that the susceptibility of hot electrons is significantly modified with streaming speed v0while susceptibilities of other two species are independent of v0.Equation(9)is the generalized form of plasma response function for electrostatic ion-acoustic waves consisting of two temperature electrons with dynamical ions and is consisted on real as well as imaginary parts.If we ignore the effect of cold electrons by assumingχc=0,we can easily reduce Eq.(9)into the result given in Ref.[46],which is confirmation of the correctness of expressions(10)–(12).For longitudinal ion-acoustic waves,the real part of dielectric constant Re(Dq(k,ω))must be equal to zero.Setting Re(Dq(k,ω))=0 and solving it for real frequency of ion-acoustic waves,we obtain Here,the auxiliary variablesΩandΛare expressed as Equation(15)shows the Landau damping rate of ion-acoustic waves in two-temperature electron plasma.The damping rate strongly depends on hot electron streaming speed and nonextensive behavior of the plasma species.It can be seen from Eq.(15)that an increase in the streaming speed reduces the damping rate significantly and this fact will also be elaborated graphically in the next section.The phenomenon of Landau damping arises during the wave-particle interaction.If there are a greater number of resonant particles having their speeds smaller than phase speed of the wave.Then the wave will transmit its energy to the resonant particles and looses its own net energy.Consequently,the wave will suffer Landau damping.However,if free energy source is present in the plasma,then the plasma wave may excite to produce growth rate of instability.In our present study,the streaming of hot electrons is the source of free energy.Therefore,an instability growth rate must arise in the ion-acoustic plasma waves.In such a situation,we have to derive the threshold condition for an unstable wave.The instability condition can be obtained as This is the threshold of the streaming speed of hot electrons above which the wave will become unstable.However,in the opposite limit,i.e.,v0<[(Ω+Λ)/Ω](ωia/k),the wave will show damping. In this section,we numerically illustrate the analytical results of Eqs.(13)and(15)in accordance with the physical situation.The inclusion of the effects of nonextensivity and streaming speed of the hot electrons(v0)significantly modify the growth rate of instability and threshold limit for unstable ion-acoustic waves.The investigation of the impact of these parameters on wave frequency and growth rate demands special attention and care.It is interesting to note that our analytical results of Eqs.(13)and(15)simply reduce to the expressions as obtained for Maxwellian distributed plasmas in the limit q→1.Interestingly,the investigations of two-electroncomponent plasmas have been reported after the satellite observations carried out by the recent spacecraft missions,for example,the FAST at the auroral region,[52–54]Viking,[55]GEOTAIL and POLAR[54,56,57]missions in the magnetosphere. Figure 1 shows the effects of(a)the cold electrons number density nc0and(b)the dynamical ion temperature Ti,on the profile of normalized ion-acoustic wave frequencyωia,versus wave number k. The black solid curve in Fig.1(a)shows real frequency of ion-acoustic waves in an ordinary electron-ion plasma,i.e.,for nc0=0,while the other three curves are drawn with non-zero cold electron density(i.e.,nc0/=0).It can be seen that the presence of cold electrons enhances the real wave frequency.This shows that frequency of ion-acoustic waves is greater in ordinary electron-ion plasma as compared to the two-component electron-ion plasma.The impact of the dynamical ion temperature on wave frequency is depicted in Fig.1(b),which shows an increase in the frequency with ion temperature.To show the influence of nonextensive q-parameter on the real frequency of the ion-acoustic wave in the two-component electron plasma,we have plotted the contour plots of normalized wave frequencyωiaagainst normalized wave number k and q-parameter in Fig.2,keeping all other parameters constant.One can observe that as we increase the value of q-parameter,the wave frequency reduces. Fig.1.The normalized ion-acoustic wave frequencyωr=ωia/ωpi against the normalized wave number k=kλDeff for varying(a)the cold electron number density nc0=0 cm−3(solid black curve),nc0=0.5 cm−3(solid red curve),nc0=1.0 cm−3(dashed blue curve),nc0=1.5 cm−3(dashed green curve)with fixed q=0.5,Ti=0.1 eV,Th=900 eV,Tc=70 eV,and(b)the dynamical ion temperature Ti=0.1 eV(solid black curve),Ti=0.2 eV(solid red curve)and Ti=0.3 eV(dashed blue curve)with fixed q=0.5,Th=900 eV,Tc=70 eV and nc0/nh0=2.5. It should be noted that q-nonextensive distribution characterizes the plasmas having plentiful concentration of superthermal particles.The wave frequency depends on the particles velocity distribution function which is controlled by the value of q-parameter in our present case.The smaller values of q-parameter,i.e.,q<1,corresponds to the more deviations of distribution from the Maxwellian distribution and ultimately show more nonextensivity.Furthermore,the presence of the superthermal particles contributes to the enhancement of phase speed and hence wave frequency.We have already discussed that nonextensive q-distribution reduces to the Maxwellian distribution in the limit q→1.This implies that frequency of ion-acoustic waves in the nonextensive qdistributed plasma is larger as compared to the Maxwellian distributed plasma.It is also observed that wave frequency increases with normalized wave number.It shows that more number of waves are passing through the unit area per second in shorter wavelength limit. Fig.2.Contour plots of normalized wave frequencyωr against normalized wave number k and q-nonextensive parameter at fixed Ti=0.25 eV. Fig.3.Contour plots of instability growth rate(normalized with ionplasma frequency)are shown against wave number and streaming speed of the hot electrons at fixed value of q-nonextensive parameter. Moreover,it should be noted that the threshold limit for unstable waves is significantly modified with q-nonextensive parameter and density of the plasma species[see Eq.(18)]. For highlighting the impact of nonextensivity on instability growth rate of ion-acoustic waves with two-temperature electrons,we have shown plots of normalized growth rate against normalized wave number at various values of nonextensive q-parameter in Fig.4.The plasma under consideration has some species with speeds smaller than the phase speed of ion-acoustic wave while some others have their speeds greater than the phase speed of the wave.The species moving with the speed closer to the phase speed of the ion-acoustic wave are known as resonant particles.These species will transfer their energy to the wave if more number of particles move with the speed greater than phase speed of the wave which ultimately leads to the instability growth rate.However,if a greater number of particles have speed less than the phase speed of the wave,then resonant particles gain energy from the wave,and the wave will exhibit Landau damping.Figure 4 shows the significant modifications in the instability of growth rate with the increase in the nonextensive parameter. Fig.4.The growth rateγia(normalized with ion-plasma frequency)against the wave number k for varying the nonextensive parameter,i.e.,q=0.35(solid black curve),q=0.55(solid red curve),q=0.75(blue curve),and q=0.95(green curve)with fixed Ti=0.1 eV,Th=900 eV,Tc=70 eV,v0=105Cia and nc0/nh0=2.5. It indicates that more energy will be transmitted from resonant particles to the wave for larger values of the nonextensive parameter during the wave–particles interactions.Hence,ion-acoustic waves in a Maxwellian distributed plasmas(i.e.,q→1)are more unstable as compared to the nonextensive qdistributed plasmas(i.e.,0 The dependence of the threshold limit of streaming speed on the density ratio can be easily observed from Fig.5.Moreover,at smaller values of q-parameter(more nonextensivity),the threshold value is high and later reduces with increasing q. Fig.5.The threshold value of streaming speed against the nonextensive q-parameter at different values of hot-to-cold electron density ratio. In summary,we have studied the dispersion characteristics and associated kinetic instability of ion-acoustic waves in an electrostatic collisionless electron-ion plasma,composed of streaming hot electrons,non-streaming cold electrons and dynamical ions.In the kinetic framework,we employed Vlasov–Poisson equations to obtain a generalized dielectric constant.The ion-acoustic wave frequency and instability growth rate in two-component electron plasma are derived and analyzed both analytically and numerically.It is investigated that the real frequency and growth rate of instability of ion-acoustic waves are significantly modified with nonextensive effects.An increase in the instability growth rate is noticed for streaming speed of the hot electrons.Schippers et al.[58]have modeled superthermal hot and cold electrons by non-Maxwellian distribution functions for the outer region of Saturn’s magnetosphere.They have made the observations by the instruments such as CAPS/ELS(0.6 eV–26 keV)and MIMI/LEMMS(15 keV–10 MeV)on board Cassini.Later,Masters et al.[60]have observed the plasma structures in Saturn’s dayside outer magnetosphere by discussing the consistency of observations relating to the inner edge of the boundary layer due to spacecraft encounter with the vortex structures of highly energetic superthermal electrons.We have applied our theoretical results on the data extracted from the Cassini outbound trajectory[58]for the Saturn’s outer magnetosphere.Our numerical results indicate weakly damped ion-acoustic mode below the threshold limit of streaming electron’s speed v0while weakly growing mode above v0,which may be observable due to the reason that its damping/growing time exceeds the wave period.Same observations were carried out by Baluku and his coworkers[61]for acoustic like plasma modes.
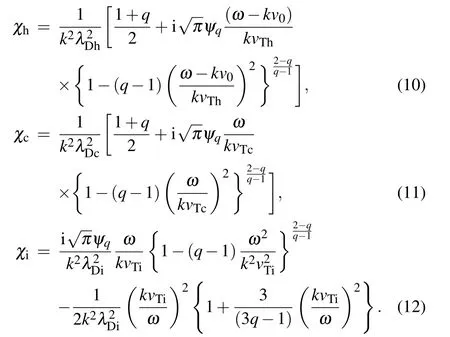

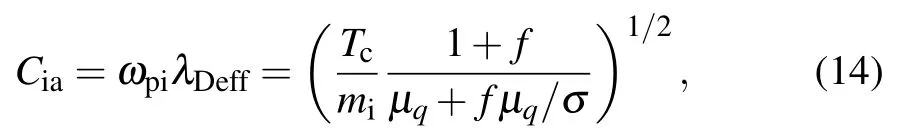
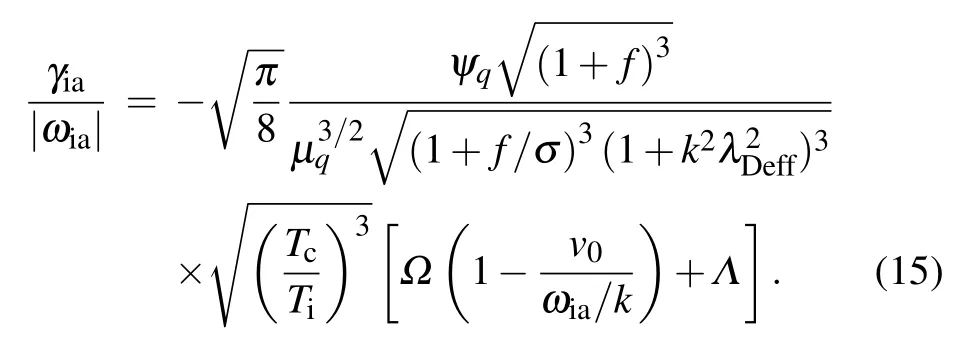

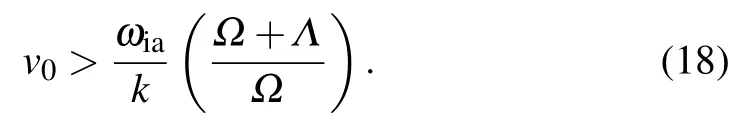
3.Results





4.Summary
杂志排行
Chinese Physics B的其它文章
- Multiple solutions and hysteresis in the flows driven by surface with antisymmetric velocity profile∗
- Magnetization relaxation of uniaxial anisotropic ferromagnetic particles with linear reaction dynamics driven by DC/AC magnetic field∗
- Influences of spin–orbit interaction on quantum speed limit and entanglement of spin qubits in coupled quantum dots
- Quantum multicast schemes of different quantum states via non-maximally entangled channels with multiparty involvement∗
- Magnetic and electronic properties of two-dimensional metal-organic frameworks TM3(C2NH)12*
- Preparation of a two-state mixture of ultracold fermionic atoms with balanced population subject to the unstable magnetic field∗
