ISSDE:A Monte Carlo implicit simulation code based on Stratonovich SDE approach of Coulomb collision∗

Yifeng Zheng(郑艺峰),Jianyuan Xiao(肖建元),Yanpeng Wang(王彦鹏),Jiangshan Zheng(郑江山),and Ge Zhuang(庄革)

School of Nuclear Science and Technology,University of Science and Technology of China,Hefei 230026,China

Keywords:Fokker–Planck equation,Stratonovich SDE,implicit,slowing down process

1.Introduction

With the development of high-performance computing technology,large-scale numerical simulation becomes popular and important in research of plasma problems,especially when investigating nonlinear and multi-scale processes.Plasma is a complex physical system which is constituted with electromagnetic fields and various charged particles,and in many plasma problems such as beam heating[1–3]and slowing down of fusion alpha particles,[4,5]collisional effects are crucial.For collisional plasma systems,a commonly used model is described by the well-known Fokker–Planck equation.However,the Fokker–Planck(FP)equation is extremely difficult to solve,either analytically or via direct numerical calculations.The main difficulty is that the FP equation is a six-dimensional partial differential equation,which requires an enormous amount of computation to integrate,and algorithms are hard to be implemented.[6,7]Usually to simplify the FP equation,researchers utilize the guiding center approximation or dimension reduction in the continuum(gridbased)methods.[8–10]Compared with the continuum methods,particle-based methods may be preferable for some reasons.For example,particle Monte Carlo methods are simple,direct and converge at a rate independent of the number of dimensions.For particle-based hybrid methods,they are efficient,especially for partially thermalized systems.[7,11]So with the Monte Carlo method and the stochastic equivalence between the stochastic differential equations(SDEs)and FP equations,we can use SDEs to investigate collisional plasma problems numerically.The stochastic differential equation theory plays an important role in many scientific fields,such as biology,chemistry,epidemiology,mechanics,microelectronics,and economics.In the past few decades,besides the field of mathematics,researchers in engineering and physics have paid more attention on numerical simulations based on SDEs.In physics research,the applications of SDE cover molecular dynamics,neurodynamics,celestial dynamics.[12–14]A significant part of SDE theory is the correlation between SDEs and FP equations.The most used SDEs are the Itˆo SDE and the Stratonovich SDE,and the corresponding numerical methods have also been developed.Besides Itˆo integration and Stratonovich integration,recently researchers developed an A-type integration which has more physical meanings and can give a natural correspondence between stochastic and deterministic dynamics.The A-type integration can also give a direct connection between trajectory dynamics and the Boltzmann–Gibbs distribution which can be used to make numerical computation less demanding.[15–18]Many studies about plasma collision have been carried out with the Monte Carlo method according to the theory of SDEs.For example,Takizuka and Abe[19]introduced a binary collision model by a Monte Carlo method for particle simulations and this model can describe a collision integral of the Landau form;Eriksson et al.[20,21]constructed a Monte Carlo operator for the orbit-averaged Fokker–Planck equation to study collisions and wave-particle interaction to improve the effectiveness of the Monte Carlo method.Cadjan and Ivanov[22]studied the absorption coefficient of a laser pulse incident into a dense plasma using the Langevin method with the Coulomb collision.Sherlock[23]used a particle-fluid hybrid Coulomb collision Monte Carlo method to study the phenomenon of electron beam incident into the plasma.Rosin et al.[7]conducted Monte Carlo simulations with the Itˆo SDE.Zhang and del-Castillo-Negrete[24]calculated the kinetic dynamic of escape electrons with a backward Monte Carlo’s method.Stevens[25]studied the energy changes during slowing down process.However,previous investigations can only be applied to Lorentzian and Maxwellian plasmas,which are inaccurate for cases with non-Maxwellian distributed plasmas.For example,in particle-in-cell(PIC)simulations,distribution functions are discretized using particles,which can be very different from Maxwellian distributions.

In the present work,the Stratonovich SDE for Lorentzian plasmas,Maxwellian plasmas are reviewed,and we have developed the Stratonovich SDE for arbitrary Klimontovich distribution function of background plasmas.We have also developed a Monte Carlo simulation program ISSDE,which is suitable for solving the SDE of Coulomb collisional plasmas.ISSDE is developed with the C++language.The design of its architecture considers the standard IO,and each part of the program is modularized so that the program is easy to be expanded and is also convenient to join the structure-preserving algorithm module.ISSDE includes the following features:(1)The evolution of the distribution function of the FP equation is replaced by the evolution of the particles’dynamic trajectories of the Stratonovich SDE so that we can describe the particle dynamics and show the random evolution trajectories of particles.(2)It can be proved theoretically that the ensemble average of results obtained by the ISSDE program and the FP equation are consistent.(3)The diffusion part of particle motion is solved by the implicit midpoint method,which guarantees the exactly energy conservation property for the diffusion term of the collision.(4)The ISSDE can also calculate the collision effect of arbitrary Klimontovich plasmas,which is more useful for calculating collisions in PIC schemes.Additionally,we simulate the relaxation process and slowing down process of charged particles injected into unmagnetized and magnetized plasma by ISSDE.We have also verified that the ensemble-averaged evolutionary behavior of the sampling points simulated by ISSDE is consistent with the evolution of the distribution function described by the corresponding FP equation.In addition,for different species of incident particles with different initial distribution function in Maxwellian plasmas,we can obtain the distribution function and ensemble average of velocity,energy,and temperature of the incident particles,which are verified with theoretical results.

2.The Stratonovich SDE for Lorentzian plasmas and Maxwellian plasmas

The primary purpose of the ISSDE simulation program is to solve the Stratonovich SDE,which is based on the stochastic equivalence of FP equations and SDEs.According to different definitions of integrals of the random variable,SDEs have many representations.The Itˆo SDE and the Stratonovich SDE are the ones that have been most used.[26]Although these two representations can be transformed from one to another,[27]the corresponding integral form,which differs from the well-known Riemann’s,must be adopted in the solving process.Therefore,in the numerical solution process,attention needs to be paid on what kind of integration it adopts.It is more preferable to model physical problems as the Stratonovich SDE because the corresponding Stratonovich integral satisfies the same ordinary chain rule as the Riemann integral.In the following,we give a short introduction of the stochastic equivalence between the FP equation and the Itˆo SDE,the transformation from the Itˆo SDE to the Stratonovich SDE,and obtain the corresponding Stratonovich SDEs based on some FP equations.For more detail information,excellent papers such as Refs.[26–29]can be referred.Considering the FP equation of Coulomb collision with the Rosenbluth MacDonald Judd(RMJ)potential,it can then receive the equivalent Stratonovich SDE.[30]We firstly present two commonly used cases as examples,which are the Lorentzian and Maxwellian plasmas.For the case of background plasma with arbitrary distribution function,a scheme based on Cholesky decomposition will be provided.

2.1.Stochastic equivalence of the FP equation and the Stratonovich SDE

The collision integral of the FP equation and the Itˆo SDE are

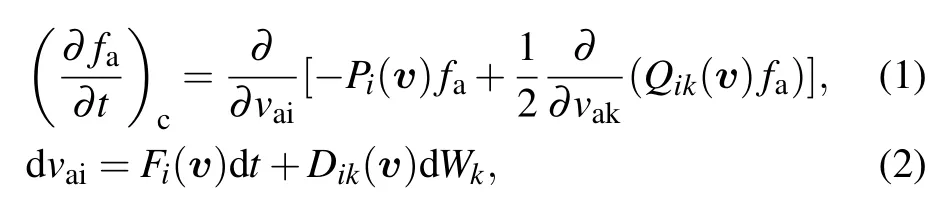
where Pi(v)is the friction coefficient,Qikis the diffusion coefficient,and fais the distribution function of particles.The velocity of the incident particle is vaiwhile v is the relative velocity between the incident particle and background particle.Here Fi(v)and Dik(v)are determined functions,and Wkis the Wiener process.[31]The stochastic process is defined on the probability space(RT,BT,PW),where T=[0,tmax]and PWis the measure induced by the Wiener process.BTis the Borelσ-algebra.[31]The solution of the FP equation is the evolution of distribution function of incident particles,while the solution of the Itˆo SDE is the trajectory of a single particle among these particles.The solution to the FP equation is stochastically equivalent to the weak solution of the Itˆo SDE if F(v),D(v)and P(v),Q(v)satisfy the following relation[20]

where the second equation means Qik(v)=Dij(v)Djk(v).

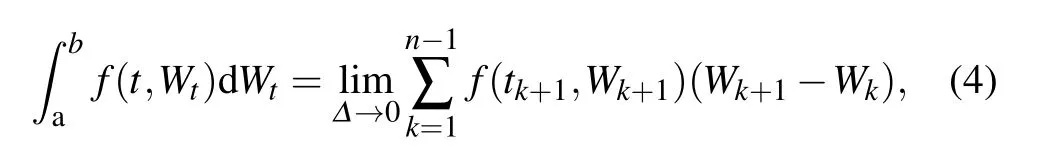
and the Stratonovich integral is defined as

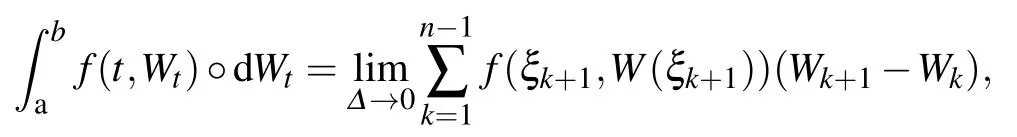
where“°”is used to represent the Stratonovich integral.The solution of an arbitrary SDE

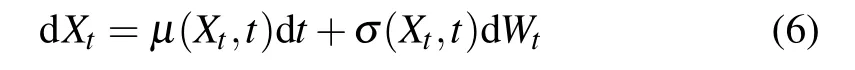
is

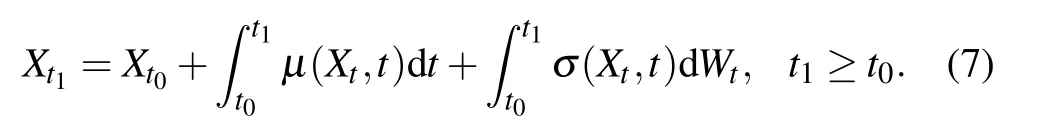
The SDE will be the Itˆo SDE if the integral in Eq.(7)is the Itˆo integral.The SDE will be the Stratonovich SDE if the integral in Eq.(7)is the Stratonovich integral.A Stratonovich integral can be presented as the sum of an the Itˆo integral with a drift term

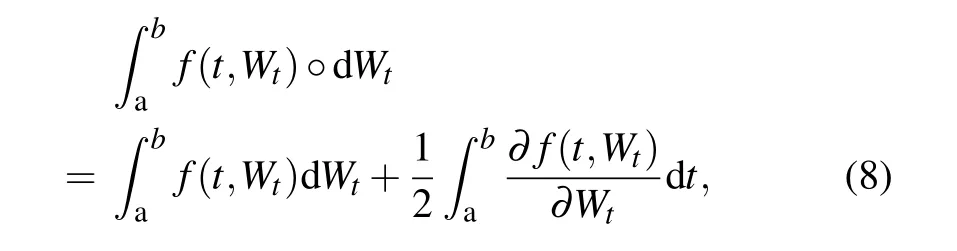
if the function f(t,Wt)satisfies the convergence condition[26]

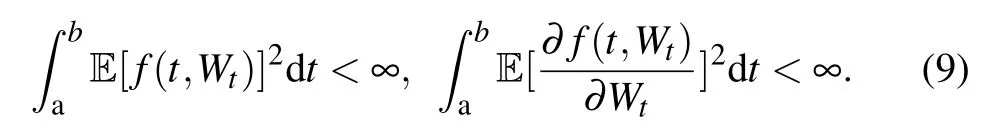
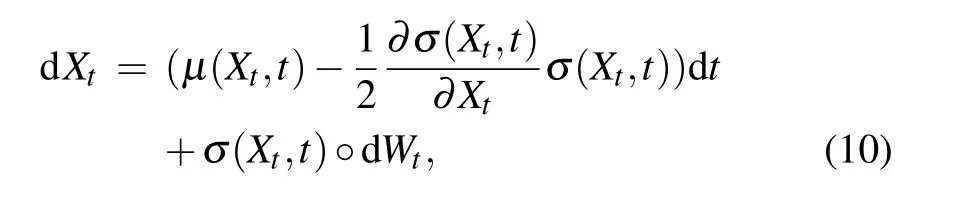
i.e.,Eq.(2)can be present in the form of the Stratonovich SDE[22]

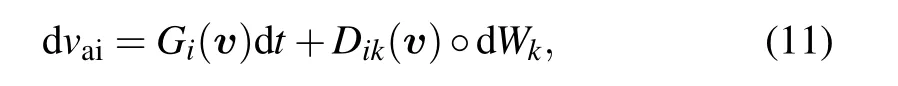
where

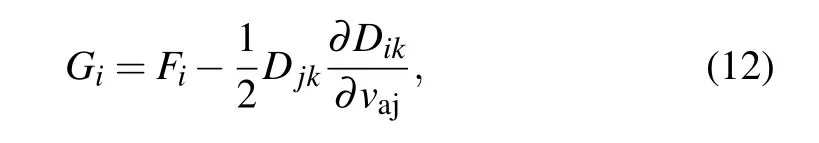
and Q=‖Qik‖and D=‖Dik‖are non-negative definite symmetry matrices.

2.2.The Stratonovich SDE for Lorentzian plasmas

In this subsection,we obtain the Stratonovich SDE for Lorentzian plasmas which is equivalent to the FP equation with the RMJ potential.The friction coefficient P and the diffusion coefficient Q of the FP equation under the RMJ potential can be referred to Refs.[21,30,32],

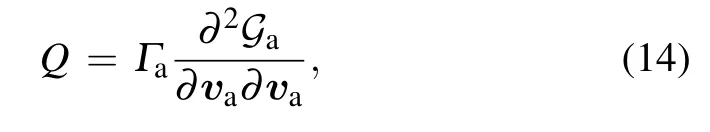
where Ha,Gaare the RMJ potential functions,

The value of fraction and diffusion parameters are dependent on the distribution function of background plasmas.An approximation can be used for a certain distribution function.For Lorentzian plasmas,the captain collision is electron-ion collision,and the background plasma can be treated as cold matter,which means that the thermal velocity is 0 m/s and the distribution function can be treated as fb(vb)∝δ(vb)∝(vb−vb0),where vb0is the velocity of background plasma.Taking the distribution function into the RMJ potential function,we can reach

The component forms of the two coefficients are

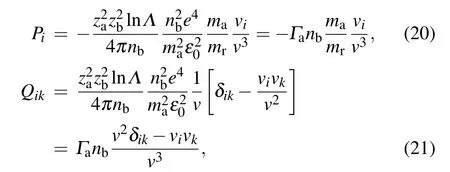
where

ma,mbare mass of species a and b,respectively;mris the reduced mass of species a and b,and za,zbare the charge number of species a and b.The number density of specie b is nb,lnΛis the Coulomb logarithm,and v=|va−vb|is the relative velocity of incident particles and the background plasma.By inserting Eqs.(20)and(21)into Eq.(3),we can obtain

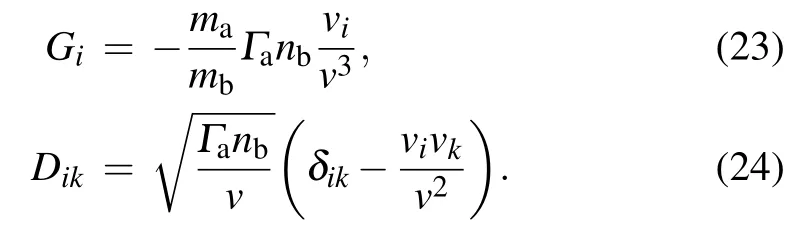
Substituting them into the Stratonovich SDE(11)yields

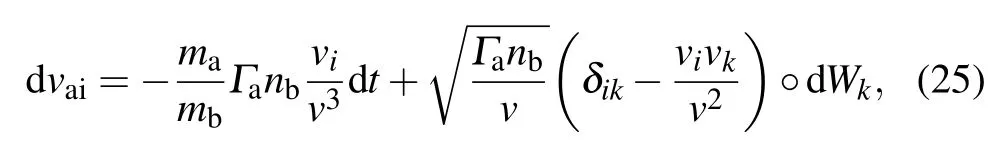
i.e.,

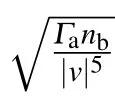
where FLis the Lorentzian force andΩ(v)=.

2.3.The Stratonovich SDE for Maxwellian plasmas

For a more general case,the probability density distribution function of background plasma is shifting Maxwellian,i.e.,

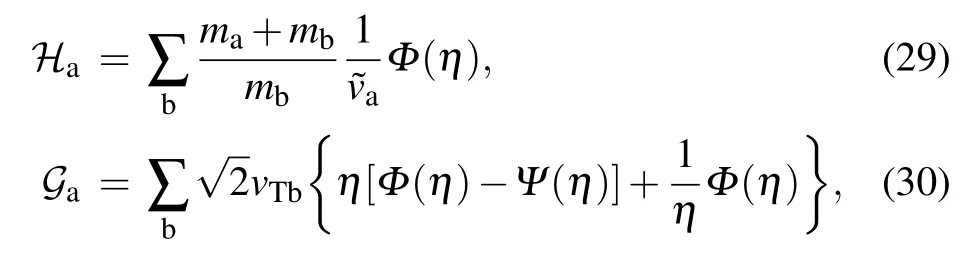
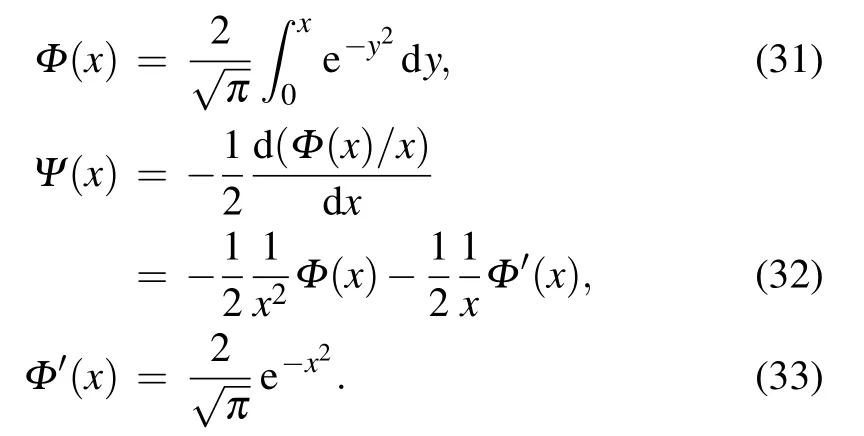
Inserting Eqs.(29)and(30)into Eqs.(13)and(14),after some calculations we have

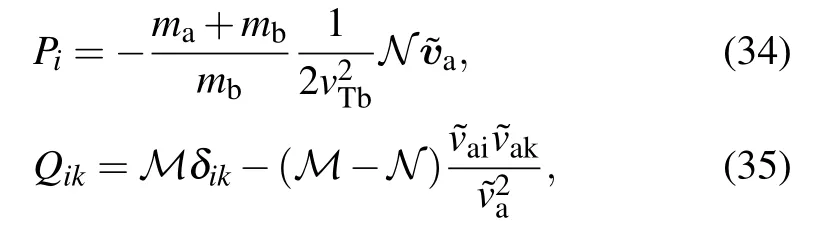
where

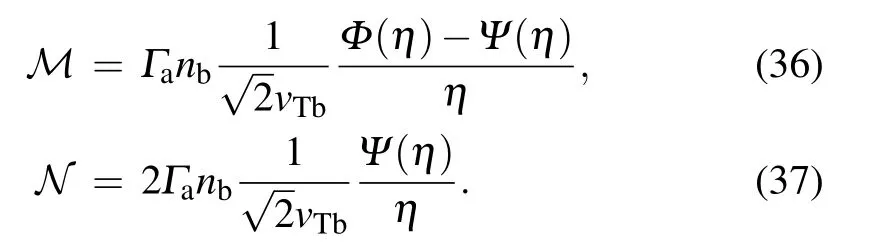
Inserting Eqs.(34)and(35)into Eq.(12),we can obtain

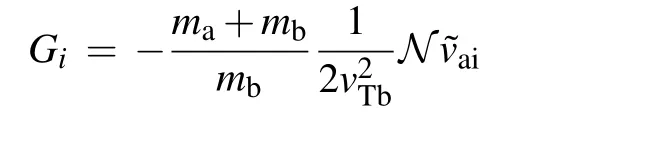
where

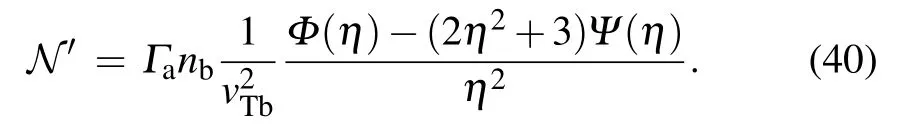
Substituting it to the Stratonovich SDE(11)yields

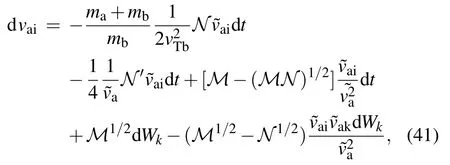
i.e.,

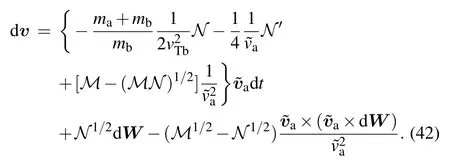
It can be extended to the cases with the external field as

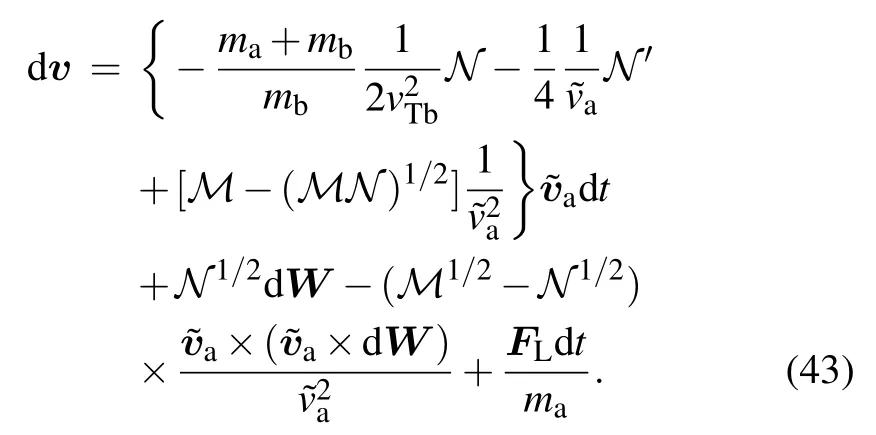
2.4.The Stratonovich SDE for an arbitrary distribution function of background plasmas

Besides the above two commonly used background particle distributions,usually we do not know the specific distribution of background particles.However,sometimes through statistical methods,we can calculate the integral of the distribution function.The PIC simulation is such a case,in which electrons and ions are discretized as marker-particles.Therefore,it is very meaningful to get the Stratonovich SDE corresponding to the background particles which obey arbitrary distribution function.In this subsection we will obtain the Stratonovich SDE for an arbitrary Klimontovich distribution function of the background particles.It covers the background particle distribution function information in Haand Ga,so as in P and Q.

For an arbitrary distribution function of background particles,assuming that the order of integration and differentiation can be reversed and we obtain

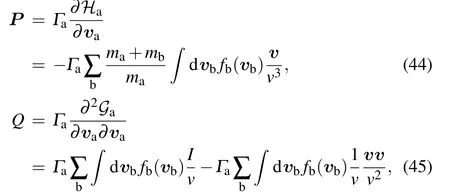
where v=|va−vb|.Therefore,we have

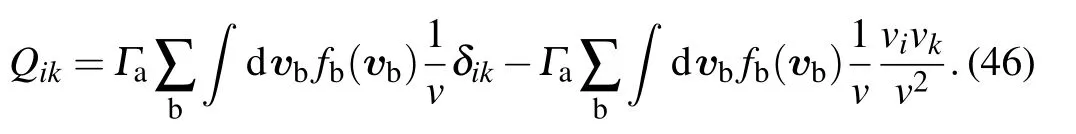
The SDE diffusion coefficient Dikand the FP equation diffusion coefficient Qikmeet Eq.(3).The decomposition of positive-semidefinite symmertic matrix Q is always possible but,in general,not unique.We provide one scheme to solve the SDE diffusion coefficient Dikaccording to Cholesky decomposition.[22]For the third-order Hermitian positive definite matrix Qik,the expression is

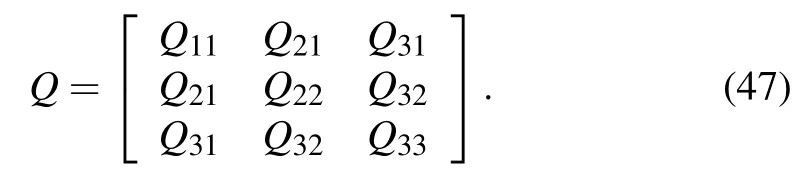
After Cholesky decomposition,the lower triangular matrix Dikis obtained as follows:

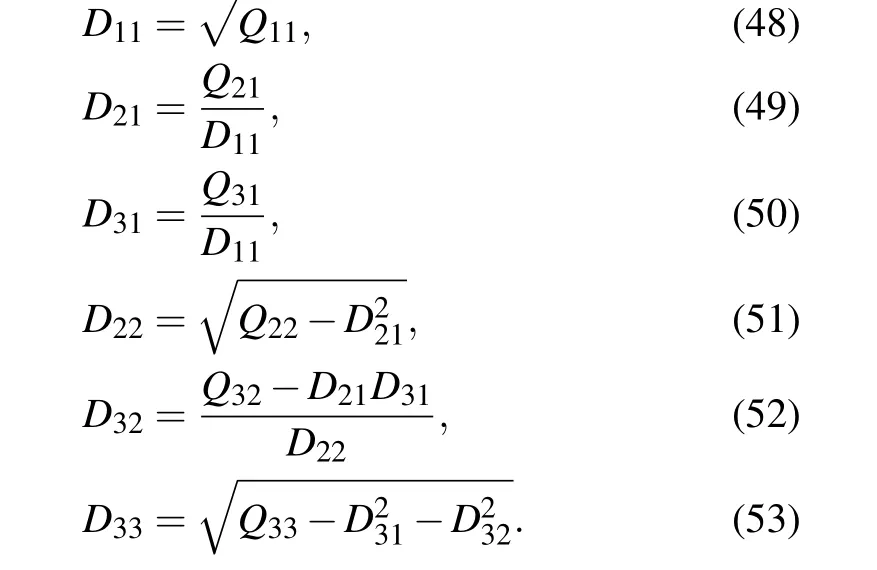
Thus,we obtain

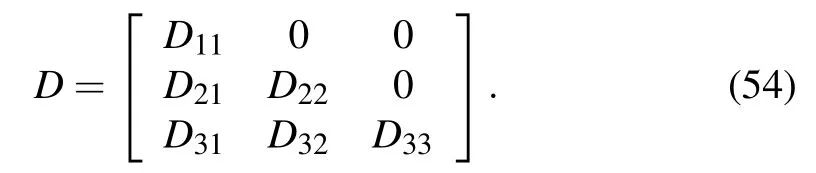
According to Eq.(12),the expression of G can be obtained.Because the integral is solved for the diffusion coefficient Q in the FP equation,the part containing the differential in G can be expressed as the differential of Q.After some calculations,we have

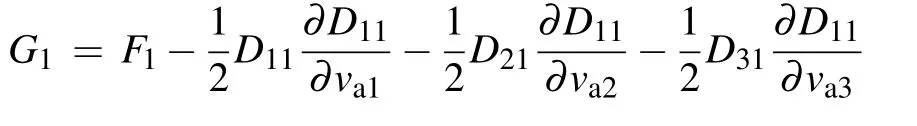
The differential of Q with respect to velocity can be expressed as

Bringing the expression of Giinto Eq.(11)and using the numerical solution or statistical methods to process the integration,we can use the Stratonovich SDE to research the dynamic behavior of incident particles with Coulomb collisions when the background particles are arbitrary distribution functions.Considering the marker-particles setting in the PIC simulation,compared with the actual situation,the number of particles used in each grid is reduced,and the value of∂Qik/∂vajcorresponding to the SDE coefficient is larger than the actual one.Thus,a correction is necessary for PIC simulation.Assuming that each marker-particle represents Nmreal particles,the values of mass and charge of marker-particle are Nmtimes as the values of a real particle.Discretise the distribution function of marker-particle using the Klimontovich representation

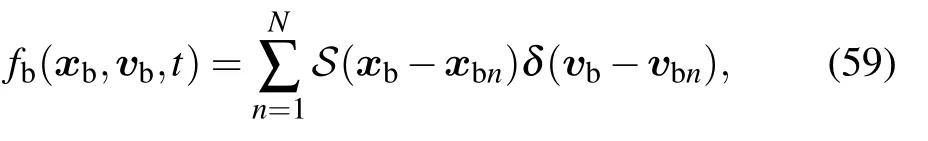
where N is the number of marker-particle,S is the shape function.[33]We obtain the values of Pi,Qikand∂Qik/∂vajof marker-particle as

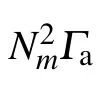
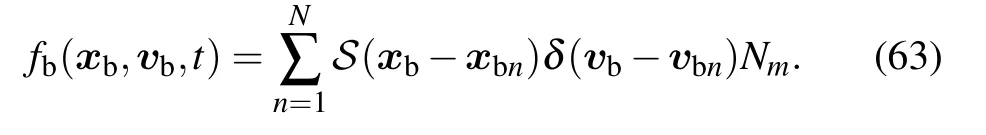
Thus,we can obtain Pri,Qrikand∂Qrik/∂vajfor real particles in the PIC simulation process

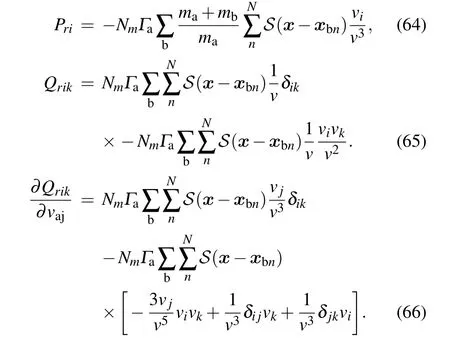
Therefore,the relationship of the coefficient between real particle and marker-particle is

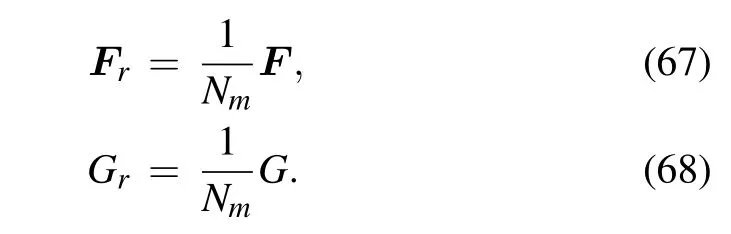
By inserting Eqs.(60)–(62)to Eqs.(3)and(55)–(57),the expression of F and G for marker-particle can be gained.Then with Eqs.(67)–(68)and Eq.(11),we can obtain the expression of the Stronovich SDE for the arbitrary distribution function of the background plasma in the PIC simulation.

3.The algorithm format and programming of ISSDE

Once we have obtained the Stratonovich SDE,according to requirement of the Euler–Maruyama method and the definition of the Stratonovich integral,the Stratonovich SDE can be discretized to construct the Monte Carlo simulation program ISSDE containing the Coulomb collision effect.For electronion collision,due to me≪mi,the change of moment and energy of ion is very small.The Lorentzian plasma model can then be used in the case that the background ion can be treated as cold,which means the thermal velocity of background ion is 0m/s.For ion-ion or electron-electron collision,the background electron and ion cannot be treated as still,so Eq.(43)will be used to take the background temperature into consideration.For Lorentzian plasmas,Eqs.(26)and(27)are the Stratonovich SDE for general types of test particles and the background plasma.This case can be more simplified according to the condition

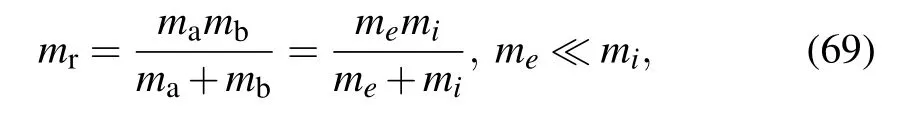
and hence

The coefficients are now

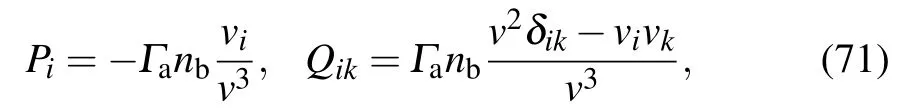
and the coefficient of the Stratonovich SDE are now

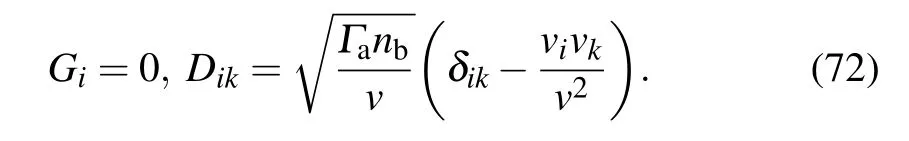
Substituting Eq.(72)into the Stratonovich SDE(11),we have

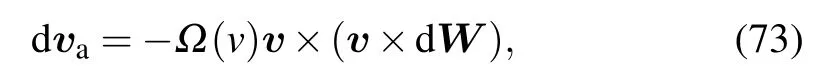
for the case with an external field,we have

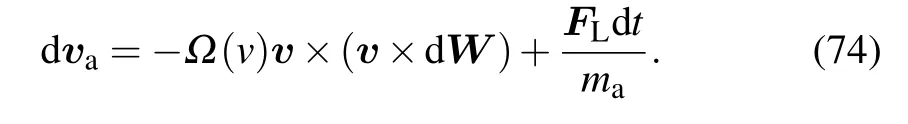
3.1.The discretization of the Stratonovich SDE

Consider the simplified Stratonovich SDE for Lorentzian plasmas that needs to be solved numerically,

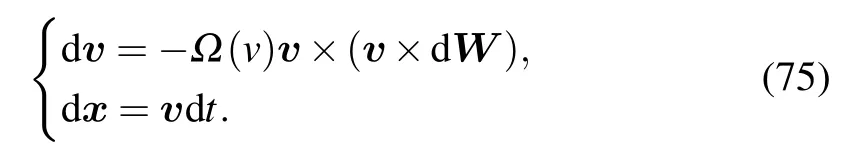
Discretizing them according to the requirement of the Euler–Maruyama method and the definition of the Stratonovich integral,we have

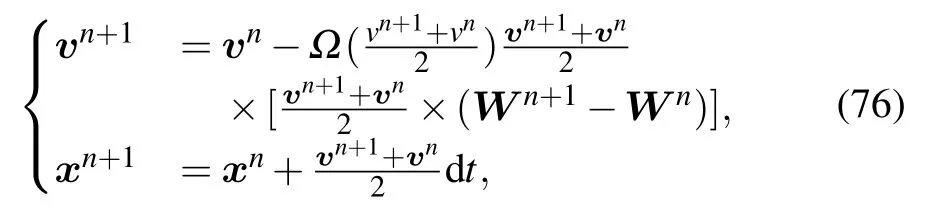
where the superscript n indicate the time step.For the algorithm of implicit midpoint format,the geometric relationship of each vector is shown in Fig.1.From the cross product relationship shown in Eq.(76),we can see

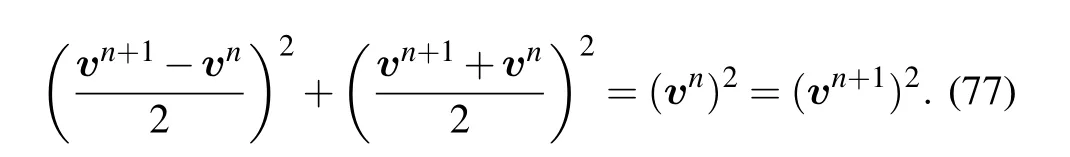
Therefore,for a Lorentzian plasma,the implicit midpoint format is exactly energy conservative.As the equation is implicit,it can be iteratively solved by the Newton–Raphson method.[34–36]

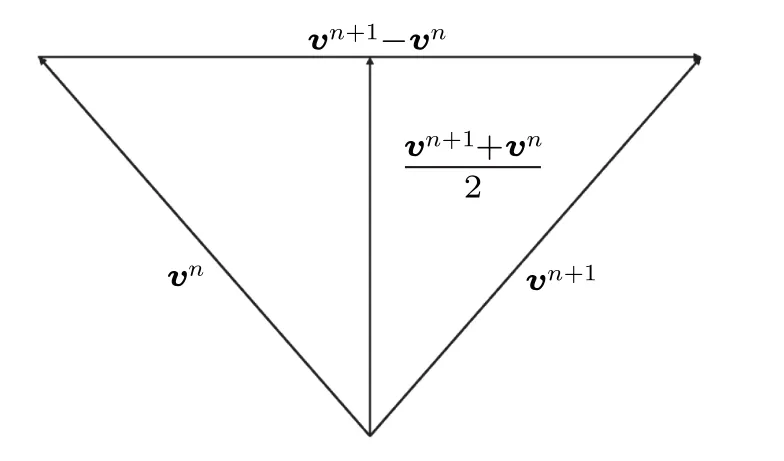
Fig.1.The geometric relationship of each vector in the implicit midpoint format in the case of the Lorentzian plasma.

For the Stratonovich SDE of a Maxwellian plasma,the discrete process is similar,while the nonlinear equations are solved iteratively by the more stable Broyden method.[37]

3.2.A splitting method for dynamics of charged particles with Coulomb collision

When there is a complex external field,using conventional algorithms to calculate the Stratonovich SDE may not have long-term stability because of the accumulation of numerical errors.In order to improve the stability of the numerical algorithm,a splitting method is used.The equations that ISSDE mainly requires to be solved are

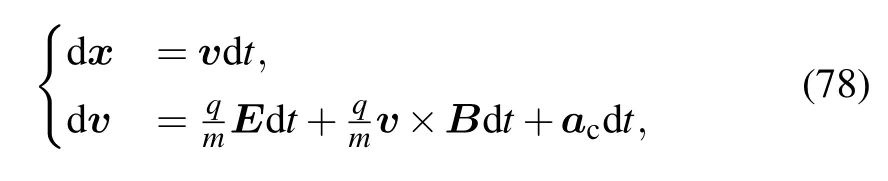
where acis the acceleration caused by the Coulomb collision.For the Lorentzian plasma,

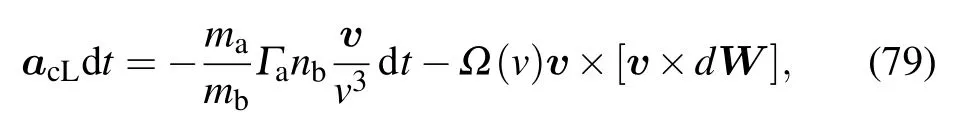
and for the Maxwellian plasma,

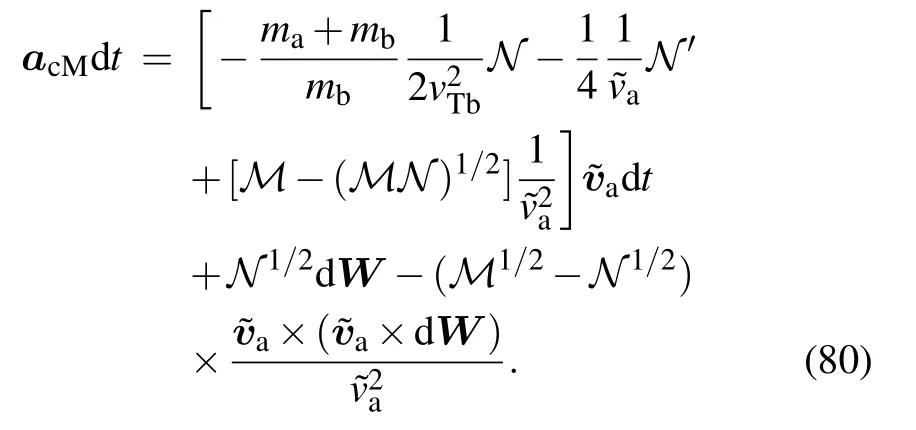
Equation(78)can be written as

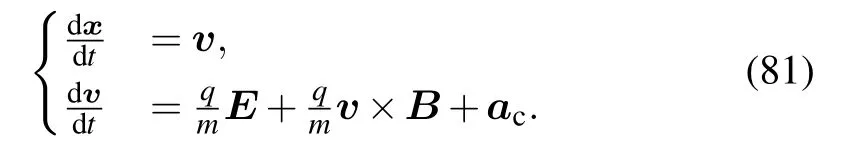
According to splitting method,the equation can be regarded as a vector field F(x,v)

Therefore,the above system can be divided into four subsystems and then solved separately.These subsystems are

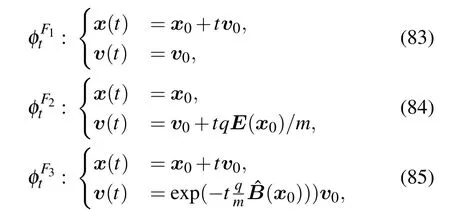
where

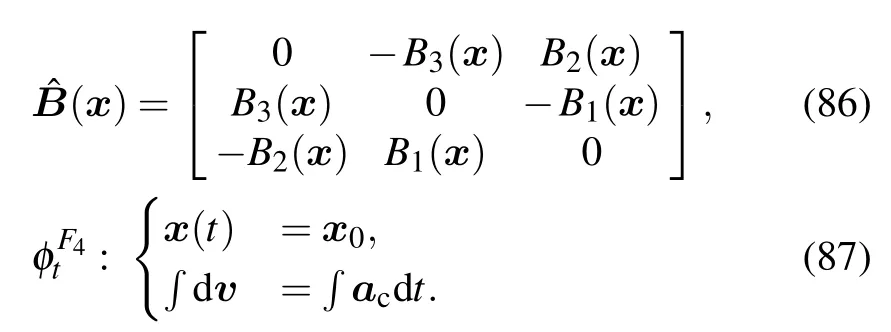
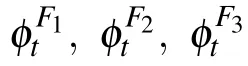
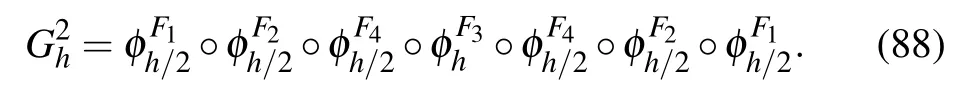
Then calculate each part separately.When there is no collision,it reduces to the normal Boris algorithm as[38]

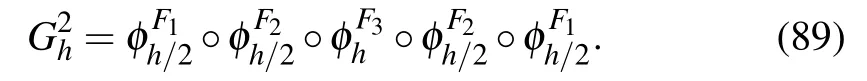
3.3.Design of the ISSDE simulation program

The ISSDE simulation program is implemented by the C++programming language and can be used on Unix-like operating systems.It comprises I/O modules,initialization modules,particle pusher modules,parallel modules,field configuration modules,external force field modules,and other extensible modules.I/O modules call library functions from Lua[39]and HDF5.[40]The input files are Lua scripts so that users can set parameters and physical problems conveniently and improve the efficiency of the program compilation.The output data is recorded and stored in the HDF5 format.It provides some static sampling methods in the initialization modules.The particle pusher module applies the algorithm given in Section 3.1 and other types of particle pusher functions,such as the collisionless volume-preserving algorithm and the Runge–Kutta algorithm.Parallel modules use the Message Passing Interface(MPI),these modules can sample the particles in parallel to speed up the calculation process.Field configuration and external force field configuration module include a variety of different configurations of the electromagnetic fields and external field,such as the radiation field and the gravity field.The extensible model is a script module that is written in Bash to enhance the scalability of the ISSDE simulation program.

3.4.ISSDE program flow chart

Figure 2 shows the flowchart of the ISSDE simulation program.The parallel program will be divided into multiple processes,each of which calculates the evolution of different particles in sequence.The I/O settings can be divided into Lua script as the input and configurations of the HDF5 file as the output.Lua script contains the basic parameters necessary for the program to run,including the basic physical parameters of the background plasma,the select switches of lots of configurations of the external fields,and the basic parameters of charged particles that need to be studied.The HDF5 file saves the coordinates and velocities of each particle in the phase space at each moment.The Wiener process and the corresponding coefficients contain the collision information of particles.We can get the value of Wtaccording to the definition of the Wiener process.The Wiener process is a stochastic process with the initial value W0=0.The increment of Wtis a random variable that obeys a Gaussian distribution with dt as the variance and 0 as the mean value.According to the definition of the Wiener process,we can see that it is possible to generate values of the Wiener process for each moment once we know the number of steps that to be calculated and the time step of evolution.The value of Wtwill then be brought into the quasi-Newton iteration loop of the main loop.Initial parameters will initialize the charged particle parameters,such as the particle’s initial position distribution,the initial velocity distribution,which is prepared for the main particle evolution loop.The main loop calculates the evolution of charged particles under the external field and the random force generated by the collision,and the data of each moment will be stored.

4.Slowing down process in Lorentzian plasmas and Maxwellian plasmas

High-speed electron beam injection is a mechanism of unmagnetized plasma heating.The electron beam undergoes a slowing down process in the plasma and raises the local plasma temperature by transferring the kinetic energy to the plasma.Therefore,it is significant to study the effective mechanism of the slowing down process.In this section,slowing down processes are simulated using the ISSDE and compared with the results given by the solution of the FP equation.Not only the correctness of the ISSDE simulation can be verified,more physical information of the slowing down process can also be obtained through the Monte Carlo numerical simulation of the ISSDE.

4.1.Slowing down process of the electron beam in Lorentzian plasmas

In the calculation of particle slowing down process,we assume that the interactions between incident electrons and between background particles are negligible.Only scattering effects of background particles to incident particles are considered.Incident particles have the same velocity and their distribution function is

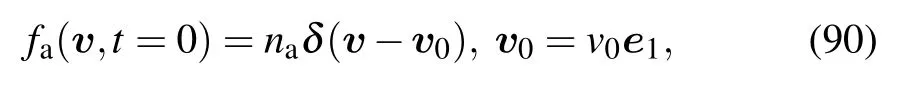
where the subscript a represents the incident particles,nais the number density of the incident particles,and v0is the velocity of the particles at t=0 with the initial direction e1.The general expression of the FP equation of the incident particles is

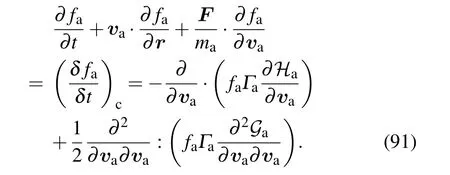
4.1.1.Theoretical approximation results of FP equation

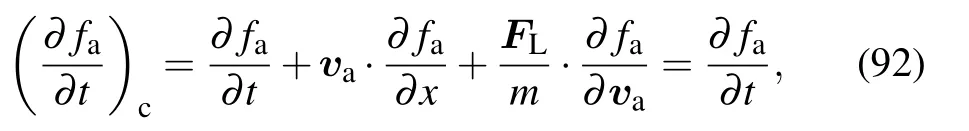
and the FP equation of the incident particle is

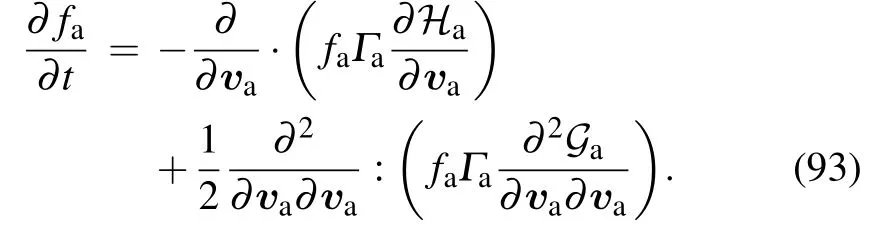
Substituting the specific form of fainto the equation and multiplying both sides with vaand then integrating it with respect to vb,we obtain

Let the background plasma obeys the following distribution

where nband vb0are the number density and bulk velocity of the background particle,respectively.Thus,the corresponding Rosenbluth potential is

Substituting Eq.(95)into Eq.(94),we have

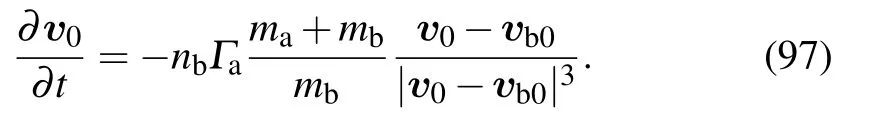
We may define the slowing down time as

and the corresponding slowing down frequency is

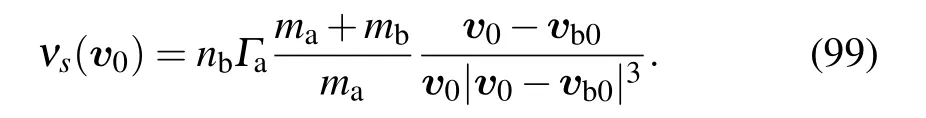
This solution is consistent with the solution in Ref.[41].

4.1.2.Numerical results of the ISSDE in an unmagnetized Lorentzian plasma

Under the parameters shown in Table 1,we sample 10048 particles in total and make a statistical average of the entire incident particle system.The collision time between particlesα andβis calculated by[42]

It shows the evolution of the averaged velocity of the incident particles parallel to the incident direction in Fig.3.The result of the ISSDE program simulation shown by the dotted line and the result of the FP equation shown by the solid line described by Eq.(97)are in good agreement.The averaged velocity of incident particles parallel to the incident direction gradually decreases and then tends to be stable.The present result is consistent with Ref.[23],which used a different method to describe the slowing down process.This proves the correctness of using the ISSDE simulation program.

Table 1.The coefficients of the slowing down process without extra magnetic field,whereτei means the collision time between electrons and ions.

Fig.3.The slowing down process of the electron beam along the incident direction(X-axis direction).The solid line represents the solution of the FP equation,while the dotted line represents the simulation result of the ISSDE.

4.1.3.Numerical results of the ISSDE in magnetized Lorentzian plasmas

For situations with external fields,the splitting method will be used and FLis added to the right-hand side of Eq.(75).For the case of considering only the external uniform magnetic field,it can be seen from Eq.(74)that the incident particle system is in conservation of energy.Let the external magnetic field is along the z direction,and the magnetic field intensity is B0=2×10−3T.For electron-ion collision,the Lorentzian plasma model is used to simplify the calculation.The electronion collision can also be calculated by the Maxwellian plasma model,but the result is similar to that of the Lorentzian plasma.The evolution of the ensemble average of the energy of incident electrons in the Lorentzian and Maxwellian plasmas is calculated by the ISSDE.The result is shown in Fig.4.The ensemble average of the energy is transferred in all directions because of the influence of the magnetic field and the Coulomb collision,and eventually all directions reach the same value,and the ensemble average of the total energy keeps unchanged.

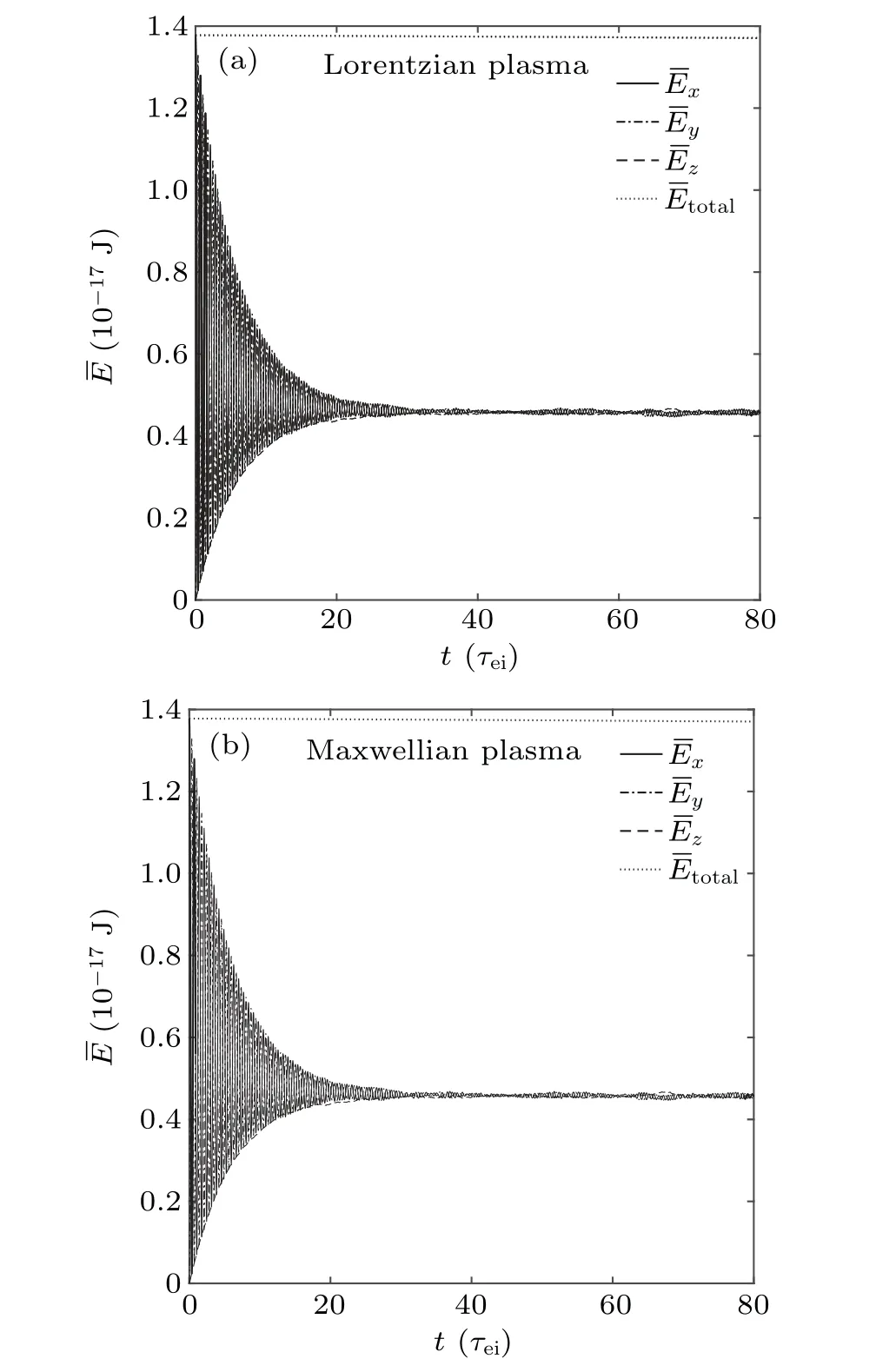
Fig.4.The evolution of the ensemble-averaged energy of the incident electron beam in all directions in the magnetized plasma:(a)the background plasma is a Lorentzian plasma,(b)the background plasma is a Maxwellian plasma.

Taking advantage of the feature that the total energy is constant in a Lorentzian plasma,we use the two-stage stochastic Runge–Kutta method R2,[43]the splitting method with twostage stochastic Runge–Kutta method R2 in the collision part,and the splitting method with implicit point format in the collision part to calculate.Then we compared the relative error of the ensemble-averaged energy.The result is shown in Fig.5.It can be seen that when the time step is 5×10−1τei,the numerical results obtained by the full stochastic Runge–Kutta method diverge,and the result of the split method is better than the result of the full stochastic Runge–Kutta method.The results of the splitting method with the implicit midpoint format in the collision part are better than the splitting method with the stochastic Runge–Kutta method.The relative error of the splitting method with the implicit midpoint format remains in the order of 10−10when the error of the Newton–Raphson or the quasi-Newton method is 10−13.Therefore,the splitting method with the implicit midpoint format in the collision part has certain advantages.For a one-dimensional one-Wiener process,stochastic Runge–Kutta methods such as CL,E1 and E2 have a convergence order of 1.5.[44,45]However,for multi-dimensional multi-Wiener process,their convergence order will become 0.5.The implicit midpoint rule will not have such a problem,and the convergence order remains 1.0.

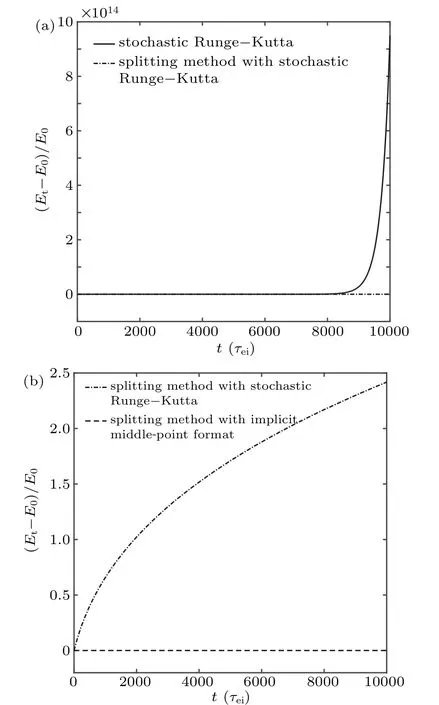
Fig.5.The relative error of ensemble-averaged energy obtained by various methods.(a)The solid line is the result of the stochastic Runge–Kutta method,the dotted line is the result of the splitting method with stochastic Runge–Kutta method in the collision part.(b)The dashed line is the result of the splitting method with implicit midpoint format in the collision part.

4.2.Relaxation process of electrons with Maxwellian distribution in magnetized Maxwellian electrons

Compared with the Lorentzian plasma,the objective function and the derivative of the objective function in the Maxwellian plasma are much more complicated.The Jacobian matrix may be sparse or singular for the inappropriate choice of stochastic variables.Thus,for the Maxwellian plasma,we adopt a more stable Broyden method instead of the Newton–Raphson method to solve the nonlinear equations.As a benchmark,the incident particles are set as electrons with the same velocity distribution as the background magnetized Maxwellian electrons.The average velocity is 0 m/s and the temperature is 8 eV.Considering the relaxation process,if the incident electrons are constantly in thermal equilibrium and keep the temperature unchanged,the correctness of the program will be proven.As shown in Fig.6,the temperature of the incident electron ensemble in all directions is mostly maintained around 8 eV.The consistency between the numerical results and the physical results shows the correctness of the ISSDE program.

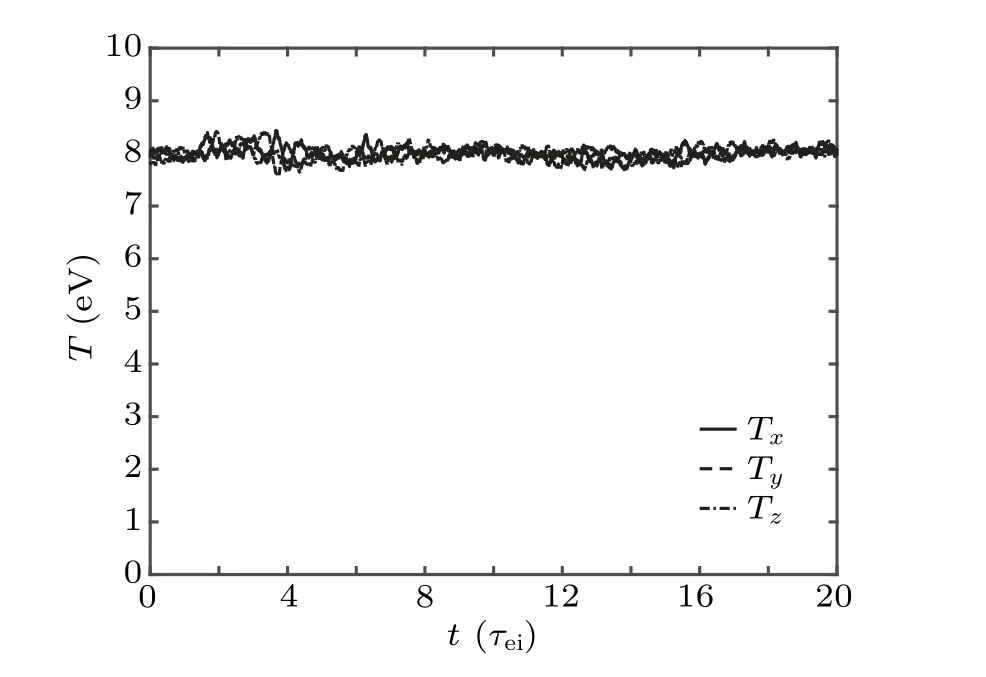
Fig.6.Temperature evolution of electrons with Maxwellian distribution in magnetized Maxwellian electrons in three directions.Hereτee is the characteristic time of the electron-electron collision.The initial temperature of incident electrons is 8 eV as same as the background electrons.

4.3.Slowing down process of beams in the Maxwellian plasma

Neutral beam injection heating is one of the fundamental plasma heating methods.The injected high-energy neutral beam will turn into a high-energy ion beam through ionization and charge exchange with the background plasma.Then the high-energy ion beam will become thermal and deliver the energy to the background electrons and ions due to the collision,eventually reach thermal equilibrium with the background plasma.Using the ISSDE program,we can simulate the slowing down process of the incident particle beam.The evolution of the incident particle distribution function and the ensemble average of the physical quantities can then be calculated.In the following subsection,we simulate the slowing down process in the magnetized Maxwellian electrons when the incident particles are electrons and ions.For electronelectron collision and ion-ion collision,the background electron and ion cannot be treated to be still,so the Eq.(43)will be used to take the background temperature into consideration.

4.3.1.Slowing down process of electron beams in magnetized Maxwellian electrons

For the case of magnetized plasma,the influence of an external field needs to be added to the equation.The parameters are set as follows:the external electric field intensity is E=0 V/m,the external magnetic field is along the z direction,and the magnetic field intensity B0=2×10−3T.The direction of the electron beam is perpendicular to the direction of the magnetic field.The evolution of the ensemble-averaged velocity with time is shown in Fig.7.Affected by the magnetic field,the momentum of the incident electrons continuously transfers around the directions that are perpendicular to the magnetic field.Due to the collision,the ensemble-averaged velocity gradually slows down,and finally drops to zero.This means that the ensemble-averaged kinetic energy of the particles is transformed due to the impact of the collision.The evolution of the ensemble average of the total energy in different directions is shown in Fig.8.

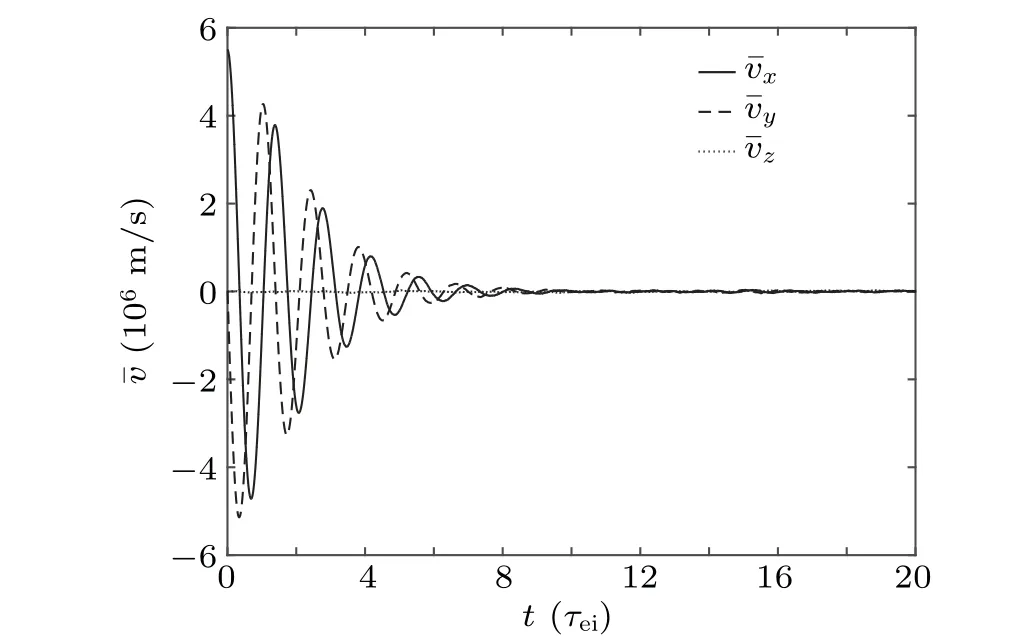
Fig.7.Ensemble-averaged velocity evolution of electron beam in magnetized Maxwellian electron in three directions,withτee being the characteristic time of the electron-electron collision.

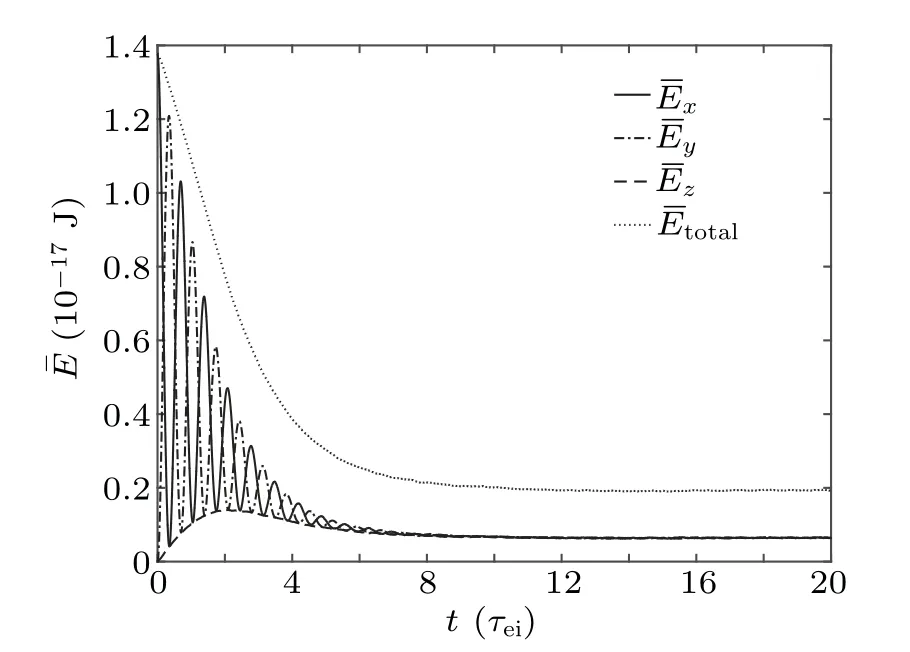
Fig.8.Ensemble-averaged energy evolution of electron beam in magnetized Maxwellian electron in three directions.The dotted line indicates the evolution of ensemble-averaged total energy.

Because of the impact of collision,the ensemble average of the total energy decreases over time,and eventually keeps unchanged.The total energy of the electron beam is transferred to the background electrons by collision.The balance of the incident electron beam can be seen by the temperature evolution of the incident electron beam,as shown in Fig.9.The total energy of the incident electrons is composed of the average kinetic energy and internal energy.During the slowing down process,part of the average kinetic energy transfers to the internal energy of the incident electrons,another part delivers to the background electrons.When the slowing down process is not violent,the average kinetic energy of the incident electrons will first transfer to the internal energy of the particles.Then the internal energy of the electrons will transfer to the background electrons in the form of heat conduction.Finally,the incident electrons and the background electrons reach thermal equilibrium.The evolution of the distribution function can reflect this more vividly,as shown in Fig.10.

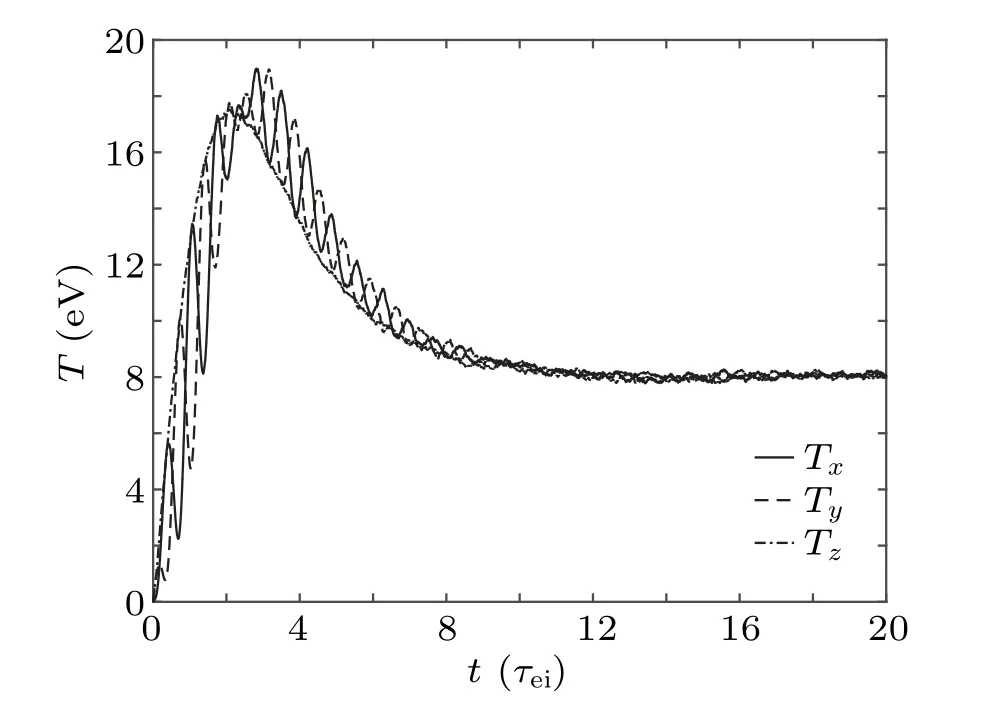
Fig.9.Temperature evolution of electron beam in Maxwellian electron in three directions.The final equilibrium temperature in the three directions is 8 eV.

Under the influence of the magnetic field,the incident electrons rotate in the velocity space.The incident electrons go through the effects of slowing down and diffuse.The diffusion process is dominant at the beginning,so the distribution function gradually spreads in the velocity space.However,when the ensemble-averaged velocity of electrons constantly decreases,the slowing down process is dominant as the electron-electron collision cross-section becomes larger.As the slowing down process of the electrons becomes dominant,the distribution function of the incident particles tends to be a Maxwellian distribution function.When the particle temperature and the background reach equilibrium,the incident particle system has a Maxwellian distribution in the velocity space,and the corresponding standard deviation is the background electron temperature.

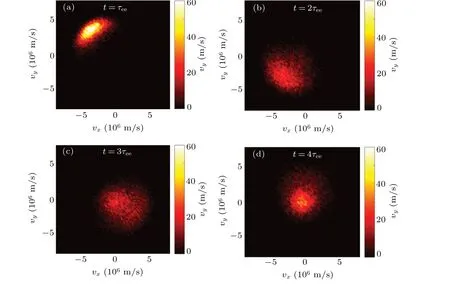
Fig.10.Evolution of distribution function of incident electron beam in magnetized Maxwellian electrons in xy velocity space:(a)t=τee,(b)t=2τee,(c)t=3τee,(d)t=4τee.

4.3.2.Slowing down process of ion beams in magnetized Maxwellian electrons

Consider an ion as a incident particle,and set the initial velocity of the incident ion to be 5.5×105m/s,the evolution of the ensemble average of ion’s velocity is shown in Fig.9.When the relative velocity of the incident ion is small,the collision cross section between the ion and the electron will be large,so that the slowing down process is dominant.Compared with the ion cyclotron period,the time scale of ionelectron collision is about 250 times smaller.It can be seen that the ensemble-averaged velocity drops to zeros in about one or two ion cyclotron periods.The evolution of the ensemble average of the total energy of incident ions is shown in Fig.12.

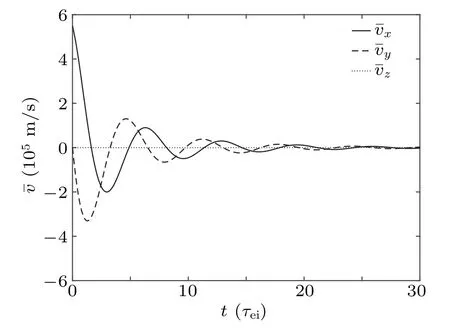
Fig.11.Ensemble-averaged velocity evolution of ion beam in magnetized Maxwellian electron in three directions for initial velocity vx=5.5×105 m/s,withτie being the characteristic time of the ion-electron collision.

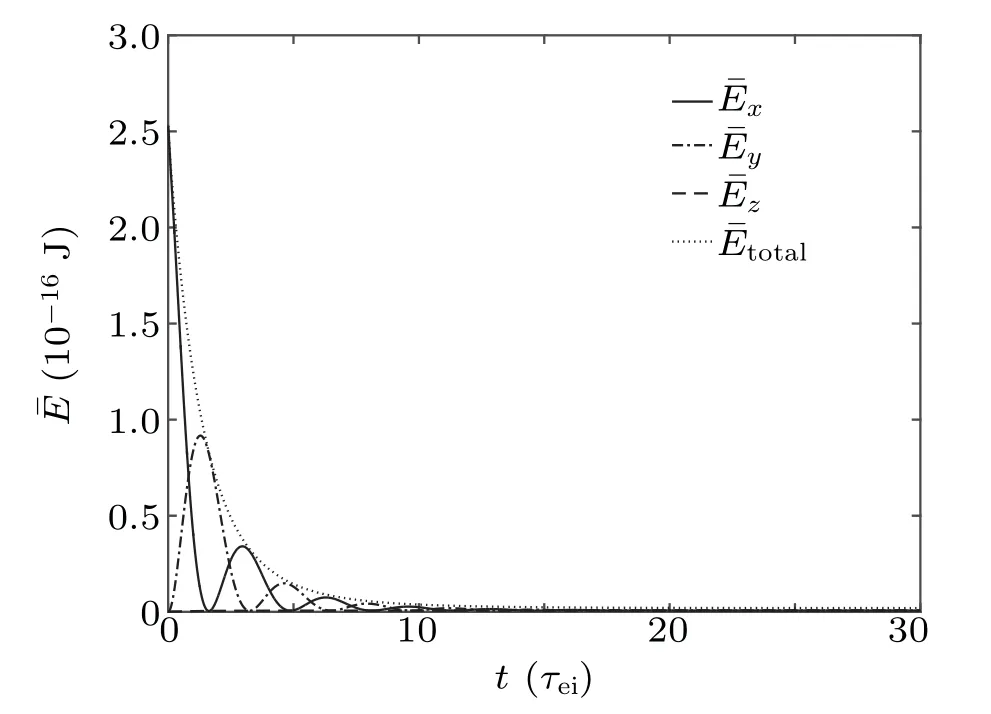
Fig.12.Ensemble-averaged energy evolution of ion beam in magnetized Maxwellian electron in three directions.The dotted line indicates the evolution of ensemble-averaged total energy.

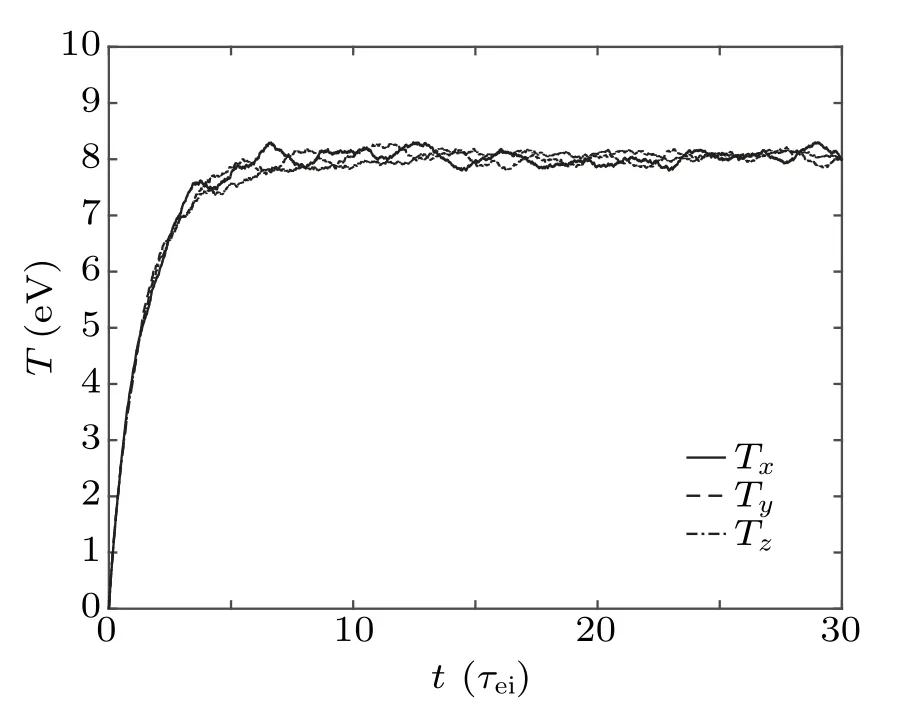
Fig.13.Temperature evolution of ion beam in magnetized Maxwellian electron in three directions.The final equilibrium temperature in the three directions is very close to 8 eV.

Similar to the electron-electron collision,the total energy of the ion transfers to the background electron through the collision,and finally the incident ions and the background electrons reach equilibrium.Compared with electron-electron collisions,in the ion-electron collision process,the diffusion process of incident ions is not dominant compared to the slowing down process,this is because in the ion-electron collision process,most of the small-angle scattering occurs.The momentum exchange and energy exchange of ions and electrons in the ion-electron collision process are rapid when the slowing down process is dominant.This can be seen from the evolution of ensemble average of the incident ion temperature,as shown in Fig.13.The rapid exchange of the momentum and energy between the ion and electron makes most of the average kinetic energy of incident ions transfer to the background electrons and a small part of the average kinetic energy transfer to its own internal energy.The final ion temperature is consistent with the background electron temperature.

The evolution of the incident ion distribution function is shown in Fig.14.The velocity in the x–y direction gradually drops to zero due to the slowing down process.The shape of the distribution function can reflect the diffusion process of collision.The diffusion process does not change as violent as the case of electron-electron collision because most of the small-angle scattering occurs.

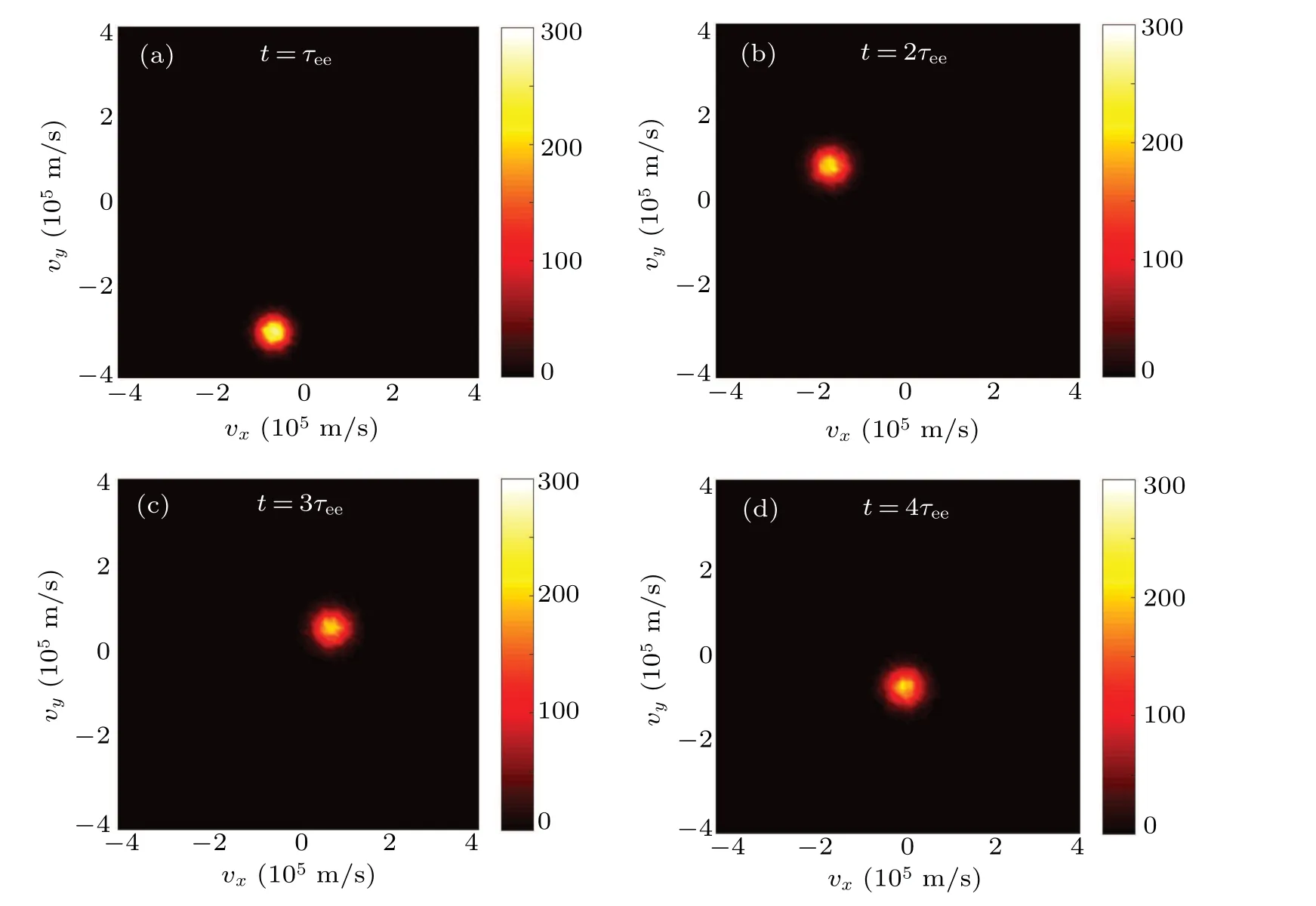
Fig.14.Evolution of distribution function of ion beam in magnetized Maxwellian electron in xy velocity space:(a)t=τie,(b)t=2τie,(c)t=3τie,(d)t=4τie.

5.Summary

Based on the stochastic equivalence between the Stratonovich SDE and the FP equation,the specific Stratonovich SDE equivalent to the FP equation with the RMJ potential is obtained.The splitting method and the implicit midpoint method are used to increase the numerical stability of the algorithm for dynamics of charged particles with Coulomb collision.The Monte Carlo implicit simulation program ISSDE for solving the Stratonovich SDE is developed to study the behavior of collisional plasma.Consider the background plasma as a Lorentzian plasma and a Maxwellian plasma.The ISSDE is used to simulate the slowing down process and relaxation process of different particles in the unmagnetized and magnetized plasmas.The consistency of the results obtained from the ISSDE simulation program with the results obtained from the FP equation about the slowing down process proves the accuracy of the ISSDE simulation program,and we can get more detailed physical information by the ISSDE.

The ISSDE simulation program can solve dynamic problems of the collisional plasma due to the simplicity of its implementation.When the distribution function of the incident particle ensemble becomes more complicated,the calculation with the FP equation becomes more difficult since the distribution function of the particle ensemble needs reconstruction in each calculation step.However,the ISSDE simulation program tracks the trajectories of individual particles directly.Therefore,once given the initial distribution of all particles in a charged particle system,all the information of the entire charged particle ensemble at any time can be obtained.

As a Monte Carlo program,the present work ignores the influence of the self-consistent field on the particle ensemble.The consideration of self-consistent field is an important physical quantity that distinguishes the single-particle model from the kinetic model.The algorithm introduced in this article can be treated as a particle pusher module with Coulomb collision in the kinetic theory model such as SymPIC.[38]The kinetic theory model describes the motion of charged particles under the effect of the self-consistent field and external field,which makes it more comprehensively to describe the behavior of plasma.However,most of the kinetic theory models are designed for collisionless plasma and it contains numerical collisions itself because of the choice of marker particle,discrete grid and shape of particles.It can significantly improve the research of advanced collisional algorithm if we apply the Stratonovich SDE to the traditional or some structure-preserving kinetic theory model and distinguish the real collision from the numerical collision clearly.We can consider the variational and canonical symplectic particle-in-cell(PIC),[45–47]and the noncanonical symplectic PIC algorithm.[38,48,49]

It is worth mentioning that according to the definition of kinetic integration which is a special limit of A-type integration,[50–52]we can also obtain the kinetic SDE equivalent to FP equations.The kinetic integration can be defined in terms of Itˆo integration,[53]

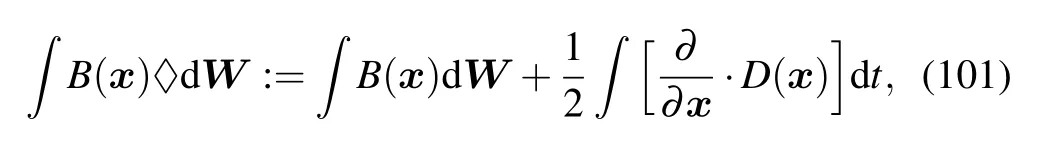
where D(x)=B(x)BT(x),“◇”is used to represent the kinetic integration.The kinetic SDE can then be obtained as follows:

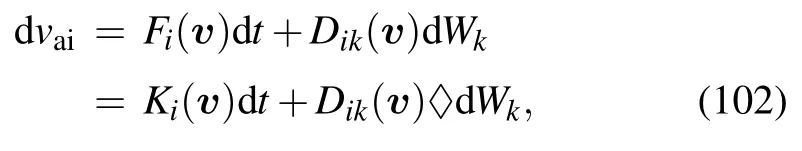
where

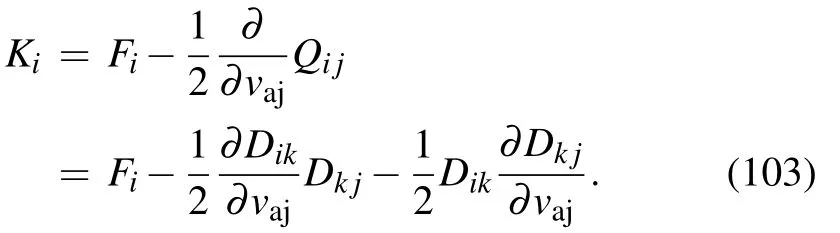
For a Lorentzian plasma,we have

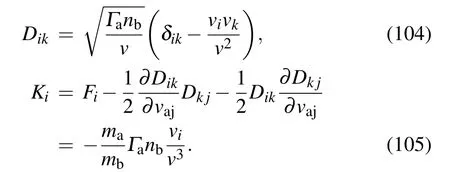
Substituting Kiand Dikinto Eq.(102)we have

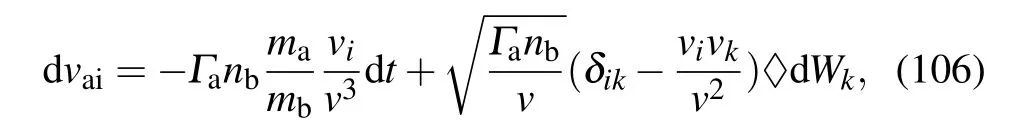
i.e.,

For a Maxwellian plsama,we have

Substituting Eq.(108)into Eq.(102),we have

i.e.,

Compared with the Stratonovich SDE,although the expression of kinetic SDE is not much different,we need to follow the definition of the kinetic integration to discrete the it in numerical simulation.H¨utter gave a definition of kinetic integration as[53]

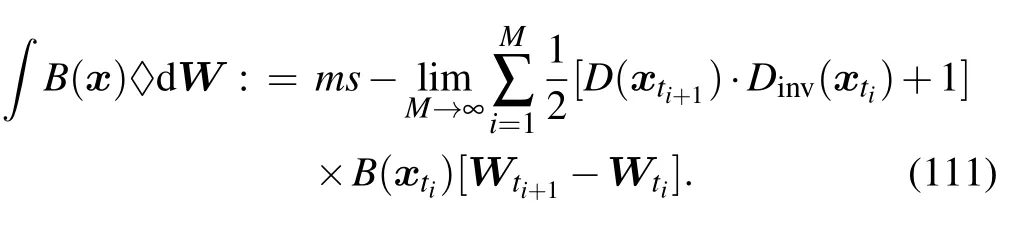
Moreover,the development of A-type integration equivalent to the Fokker–Planck equation with RMJ potential and the corresponding numerical methods can be good directions for research in plasma physics.In systems in which the drift term originates from a gradient of a potential that is mediated through the diffusion or mobility tensor,i.e.,

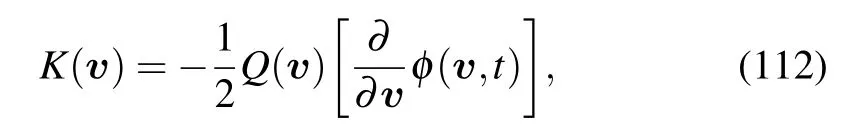
the“Boltzmann–Gibbs distribution”

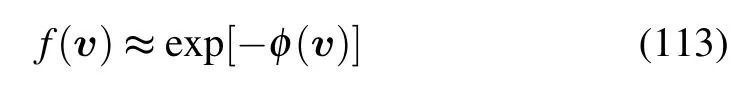
is a stationary solution of Eq.(102).When we know expressions of K(v)and Q(v),we may calculateφ(v)as

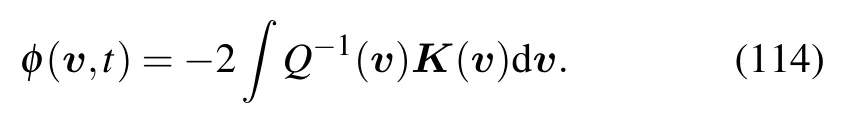
It may not be very easy to calculateφ(v)as expressions of K(v)and Q(v)are very complicated.The process of constructing the A-type SDE may be similar to that of the kinetic SDE.We will report related results elsewhere.