High-resolution three-dimensional atomic microscopy via double electromagnetically induced transparency

Abdul Wahab

1National Laboratory for Physical Sciences at Microscale,Shanghai Branch,University of Science and Technology of China,Shanghai 201315,China

2CAS Center for Excellence and Synergetic Innovation Center in Quantum Information and Quantum Physics,University of Science and Technology of China,Hefei 230026,China

Keywords:electromagnetically induced transparency,transparency windows

1.Introduction

Electromagnetically induced transparency(EIT)is a nonlinear process in which a non-transparent medium is rendered transparent through electromagnetic fields.[1,2]The EIT is usually observed in a three-level system.When an additional week electromagnetic field is added in a four-level EIT system,two simultaneous transparency windows are created,[3–6]so-called double EIT(DEIT).DEIT enables two simultaneous signal fields to be propagated with negligible loss and increases the interaction duration between the pulses due to lower group velocities.These characteristics render DEIT as good choice for various applications[7–9]in the field of quantum optics and quantum communication.

A variety of schemes have been proposed to achieve DEIT,e.g.,MacRae et al.proposed an experimental scheme[4]for DEIT using a tripod system in rubidium vapor.They have shown that DEIT could be used to control the group velocities of two signal fields.Alotaibi and Sanders[10]have developed a similar four-level tripod scheme for double-double EIT and demonstrate that nonlinear optical susceptibility can be improved to the order of 1000.Likewise,Wang and his colleagues[11]proved experimentally that light can be improved by DEIT coherence.

In past few decades,the progress of quantum technologies has play a major role in localization of moving atoms[12–14]through standing-wave fields(SWFs),which is a wide area of research with applications in various fields,i.e.,Bose–Einstein condensation,[15]laser cooling and neutral atom trapping,[16]atom nano-lithography.[17]Similarly,an optical-mask technique is used to study the atomic density distributions in optical lattices[18]and sub-Doppler cooling in reduced-period optical lattice geometries.[19]

Multiple pioneering studies on atom localization have been proposed by laser manipulation,where the position of moving atoms through SWFs can be determined by Ramsey interferometry,[20]performing a phase measurement on a prob field[21–23]and all other optical approaches.[24,25]Likewise,the atom localization has been introduced using the Autler–Townes microscopy technology,[26]spontaneous emission of photons and monitoring the phase and amplitude of absorption spectra.[27–29]

In the current decade,the interest in high-dimensional atom localization has been increased due to its unique aspects and enormous applications.Many schemes have been proposed based on probe absorption,[30–32]spontaneous emission[33,34]and squeezed vacuum.[35]Ivanov et al.[36]proposed a four-level tripod system and used the population of the excited states to localized an atom in two dimensions.They applied two orthogonal SWFs(OSWFs)to obtain localization by adjusting parametric conditions properly.Further,atom localization has been studied in the case of four-level closed loop[37]and N-type[38]systems by monitoring probe absorption and Raman gain process,respectively.

Furthermore,three mutually OSWFs have been studied to achieve 3D atom localization via probe absorption in a cascade four-level atomic system.[39]Atom localization in 3D has also been investigated via excited-level population,[40]via three-wave mixing in V-type three-level atoms,[41]closed loop KR5 level system,[42]double two-level scheme,[43]via Kerr nonlinearity[44]and in surface plasmon polaritons.[45]Based on these findings,it is known that the spatial resolution of the atomic position can be enhanced and that maximum probability of detecting an atom position could be achieved by considering a high dimensional scenario.

Nonetheless,none of them[40–44]suggested DEIT process for atom localization.Motivated by this,we show a new approach of 3D-atom localization using DEIT.In our objective research,a four-level tripod atomic system is controlled via a probe field,signal field and position dependent control field.By properly controlling system parameters,we notice the single atom’s position information in a 3D volume space.Furthermore we also incorporate the effect of Doppler shift on 3D atom localization.Our proposed scheme not only offers a new way to achieve a high-precision atomic position,but also provide many potential applications.

Our research work is organized as follows.In Section 2,we present our model and mathematics.Using density-matrix approach we find the optical susceptibility of the system.In Section 3 we use optical susceptibility and show our results for high dimensional(3D)atom localization.In Section 4 we see the influence of Doppler broadening on 3D atom localization.In Section 5 we provide the possible experimental realization scheme for our four-level87Rb atomic system.Finally,In Section 6 we provide our conclusions.

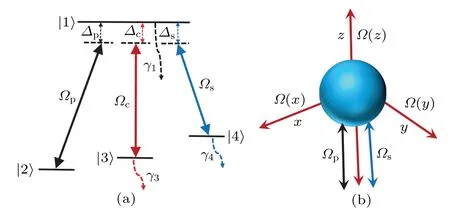
Fig.1.(a)Schematic of the four-level tripod atomic system.Transitions are controlled by probe field Rabi frequency(Ωp),control field at Rabi frequency(Ωc)and signal field at Rabi frequency(Ωs)between levels|2〉↔|1〉,|3〉↔|1〉,and|4〉↔|1〉,respectively,whereΔp,Δc andΔs are the detunings of the given applied fields;γ1,γ3 andγ4 are the decay rate of level|1〉,|3〉and|4〉.(b)Movement of an atom along the z-axis and interacting with three OSWFs in 3D space.

2.Model and theoretical approach

In this section we describe our model and theoretical approach.We assume a four-level tripod system with one upper and three lower levels,as shown in Fig.1.The upper level|1〉is attached with lower levels|2〉,|3〉and|4〉.The signal field(Es)with Rabi frequencyΩsis applied between the transition levels|4〉↔|1〉,probe field(Ep)having Rabi frequencyΩpis applied between the transition levels|2〉↔|1〉,whereas the control field(Ec)with Rabi frequencyΩcis applied between the transition|3〉↔|1〉.HereΔs,ΔpandΔcare the detunings of the respective fields.

In our objective model,the detunings of the probe and signal fields are equal,but vary from the detuning of the control field.A new transparency window emerges on both probe and signal absorption profiles to enhance optical properties in either linear or nonlinear dimensions.The existence of a transparency windows in the absorption profile of both fields enables as an alternate point of action,which could proceed to a more efficient response of the atom and could be helpful for localization of an atom.Now the control field Rabi frequency Ωcin our tripod system is the superposition of three OSWFs and can be described as[46,47]

with

where asΩc(x),Ωc(y)andΩc(z)are also the superposition of two OSWFs aligning along the x,y,and z directions respectively;where ki(i=1–6)show the wave vectors related with wavelength(λı)as ki=2π/λı;θ,ηandξrepresent the phase shifts of SWFs corresponding to the wave vectors k1,k3and k5,respectively.

Now using rotating-wave approximations the timeindependent Hamiltonian of the system is written as

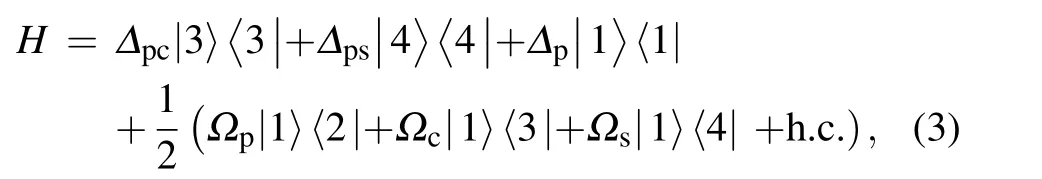
where h.c.shows the Hermitian conjugate.WithΔxy:=Δx−Δy.The system parameters corresponding to the density matrix read

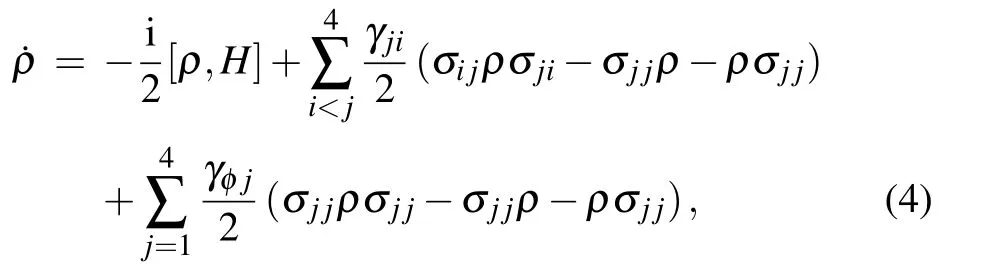
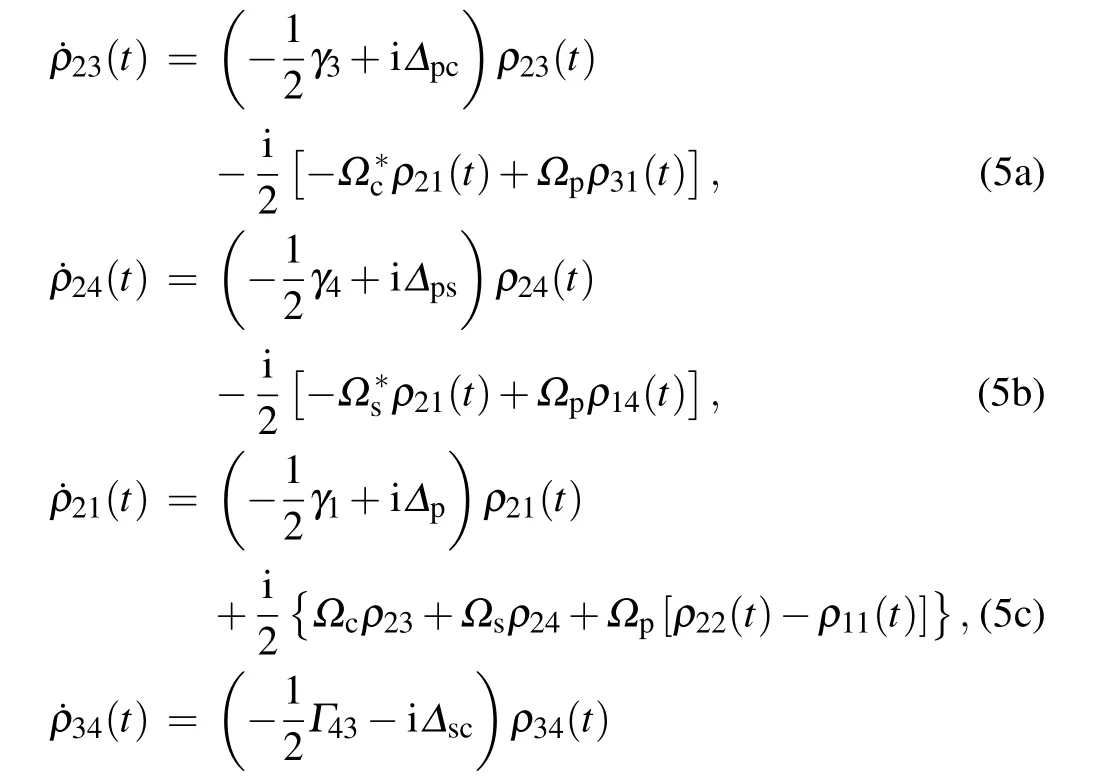
The equations of motion for population are expressed by the Eqs.(5g)–(5j).Our aim is to find atomic position information using the optical susceptibility of the medium.To do this,we find the solution for off-diagonal density matrices(ρ21)and(ρ41)for probe and signal fields.However,it is impossible to find a steady-state solution of(ρ21)and(ρ41)without making any assumptions.Therefore,we assume constant populations such asρ22≈ρ44≈0.5 in our proposed system.This presumption renders the equations resolvable analytically,as equations of motion of the population Eq.(5b)effectively decoupled from the motion equations for coherence Eq.(5a).Also,we assume that

is always valid for all selected values ofΩc,Ωp,andΩs.This assumption allows theρ31coherence to be decoupled from other coherence,which is perfored by eliminating theΩpρ31andΩ∗pρ31terms from˙ρ34and˙ρ23in Eq.(5a)and Eq.(5d),respectively,because their impact is weak in comparison to other terms.As a result,the off-diagonal density-matrix element in the probe fieldρ21can be calculated by

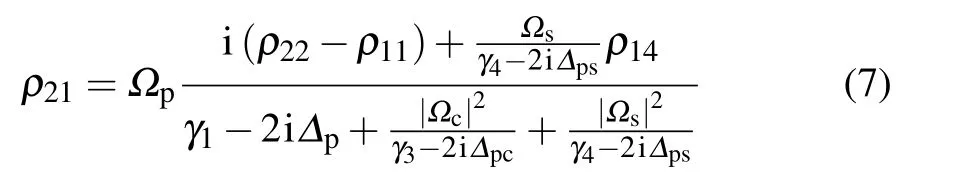
with

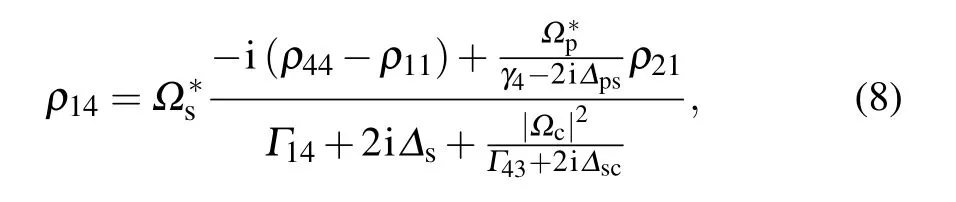
whereΓkl=γk+γl.Substituting Eq.(8)into Eq.(7),we can write the optical response of the probe field as

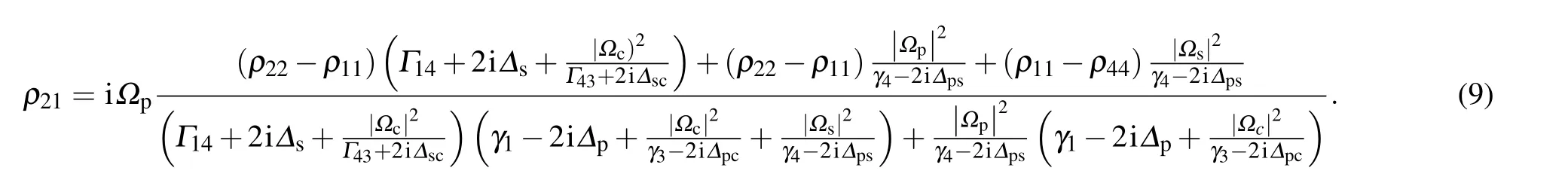
Therefore,we can calculate the optical susceptibilityχp,which is related to the density matrix elementρ21and can be written as

Similar to the probe field,the signal field effective optical susceptibilityχscan be define as

Here,N shows atomic number density,with d21and d14are the dipole moments in Eqs.(10)and(12),whereasε0is permittivity of free space and¯h is Planck’s constant.Equations(10)and(12)represent the key findings of the paper to allow one to measure the position of the atom.Equations(10)and(12)show that the precision measurement of an atom depends on system parameters,i.e.,the amplitudes and relative phases of the SWFs.We will explain these issues in more detail in the following section.

3.Numerical results and discussions

In this section,we discuss our numerical results for atom localization in 3D space.Our results are based on Eqs.(10)and(12).We use Eqs.(10)and(12)and see how 3D atom localization via DEIT is achieved by varying different system parameters.

3.1.The first case:Probe absorption spectrum

In this subsection,we use probe absorption(Imχp)spectrum of Eq.(10)and plot our results versus normalized positions(kx/π,ky/π,and kz/π)and show that how precise 3D atom localization is achieved by varying different system variables.

Before going to atom localization we first understand the physics of DEIT.In our case,we take nearly equivalent Rabi frequencies for both the probe and the signal fields,such that each field shows the same behavior.The two weak fields(signal and probe)will propagate through the medium with group velocity lower than the speed of light.This system generates two simultaneous transparency windows for two weak fields.The first transparency window appears atΔpc=0 whereas the second window occurs atΔps=0.Both the fields(signal and probe)have the same optical properties due to double transparency windows.

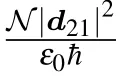
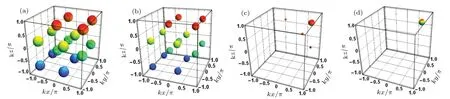
Fig.2.Plot for probe absorption(Imχp)versus normalized positions(kx/π,ky/πand kz/π)for(a)Ω1=Ω2=Ω3=3.5γ1 and(b)Ω1=Ω2=Ω3=2.5γ1 with kj=κ(j=1–6)andθ=η=ξ=0,(c)θ=η=ξ=π/3 and(d)θ=η=ξ=π/2.7 withΩ1=Ω2=Ω3=2.5γ1,k1=k3=k5=0.85κ,k2=k4=k6=κ.The other parameters from(a)–(d)are taken asΔs=Δp=9 MHz,Δc=0,Ωs=0.3γ1,Ωp=0.2γ1,ηp=1,ρ22≈ρ44≈0.5,γ1=1 MHz,γ3=40 kHz,andγ4=10 kHz.

Our next task is now to obtain a single,precise position of an atom with high spatial resolution.To the best of our knowledge,the wave vectors and phase changes of the related fields play a significant role in controlling the precision position of atoms.[32,43,48]In Figs.2(c)and 2(d)we plot isosurfaces for various values of wave vectors and phase shifts of the relevant fields.In the case of k1=k3=k5=0.85κ,k2=k4=k6=κ andθ=η=ξ=π/3(see Fig.2(c))we clearly see that 16 small sphere is converted to 4 and the detection probability of finding the atom increases from 1/16 to 1/4.Now by settingθ=η=ξ=π/2.7,as shown in Fig.2(d)we notice that the small spheres appearing in Fig.2(c)completely disappear and a single precise sphere appears in cubic space.This result shows that the conditional position information of an atom in volume space is increased up to 1,in other words,the high precision position of an atom in 3D space is achieved efficiently.These findings indicate that the 3D atom localization depends on the phase shifts of applied fields.

3.2.The second case:Nonlinear absorption spectrum

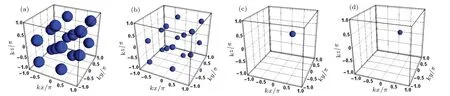
Fig.3.Plots for the nonlinear absorption spectrum(Imχp=0.6)versus normalized positions(kx/π,ky/πand kz/π)for(a)Ω1=Ω2=Ω3=4γ1 and(b)Ω1=Ω2=Ω3=3γ1 with k j=κ(j=1–6)andθ=η=ξ=0,(c)θ=η=ξ=π/8 and(d)θ=η=ξ=π/16 with Ω1=Ω2=Ω3=3γ1,k1=k3=k5=0.6κ,k2=k4=k6=κ.The other parameters from(a)–(d)are the same as those in Fig.2.

As in Subsection 3.1 we can see that the control field intensity and relative phase changes play a vital role in precision position measurement of an atom.Here we use the same procedure and see the impact of these parameter on atom localization.First,we can see the influence of control field intensity.For the case ofΩ1=Ω2=Ω3=4γ1,kj=κ(j=1–6)and θ=η=ξ=0,we see the 16-sphere-like pattern with the same localization precision in different subspaces.This shows possible positions’information of an atom in volume space.Nevertheless,owing to high size of each sphere the resolution is poor and the probability is 1/16[see Fig.3(a)].Moreover,under the condition ofΩ1=Ω2=Ω3=3γ1,as shown in Fig.3(b),we can easily see that size of each sphere in the subspace is becoming smaller,which indicates a precision enhancement.This means that increasing control field intensity would have a destructive effect on the precision measurement.The reason for this is that the control field will affect the nonlinear absorption.

Now we see the role of phase shifts on atom localization.Under the condition of k1=k3=k5=0.6κ,k2=k4=k6=κ andθ=η=ξ=π/8,as shown in Fig.3(c)we notice that by introducing the phase shifts of coupling field,15 small spheres completely disappear and only a single sphere appears in volume space.This shows the enhancement of an atom localization from 1/16 to 1.Now by further settingθ=η=ξ=π/16(see Fig.3(d))we can see a very precise sphere in 3D volume space.This implies that the probability of locating the atom in a single cycle of SWFs is improved to 100%.

3.3.The third case:Gain spectrum

In this subsection,we show our results of 3D atom localization using gain term of Eq.(10).As we know,the third term of Eq.(10)is directly related to|Ωs|2,which will represent gain if population in transition level|4〉is greater than the transition level|1〉in our system.

First we explain the physics why a net gain is observed in Eq.(10)even we assume constant populationρ22≈ρ44≈0.5 in our analytical solution.The reason is that if we take the Rabi frequencies of signal(Ωs)and probe field(Ωp)to be exactly equal,then both the terms(second and third)will cancel each other due to the same and apposite sign,so no net gain is observed.As in our case,the Rabi frequency of signal field(Ωs)is slightly higher than the frequency of probe field(Ωp)so population changes,due to this we observe a gain in our system.This gain is not due to population inversion,but to the quantum coherence effect of the driving signal field.We use the imaginary part of this gain term and see atom localization 3D volume space.

As we see in Subsections 3.1 and 3.2 the intensity and relative phase shifts of the control field are essential parameters for atom localization.Here,we take the same method and see the effect of these parameter on atom localization.

Similar to the above results,we first see the influence of control field intensity on atom localization.Under the condition ofΩ1=Ω2=Ω3=3.5γ1,kj=κ(j=1–6)and θ=η=ξ=0,we see 16 sphere-like shapes of high size distributed in volume space.This exhibits the possible position information of an atom in volume space as in Fig.4(a).Moreover,when we chooseΩ1=Ω2=Ω3=3γ1,one can easily see from Fig.4(b)that the diameter of each sphere is becoming smaller,which indicates a precision enhancement.These findings suggest that the control field intensity would have a detrimental impact on atom localization.

Fig.4.Plots for gain spectrum(Imχp)versus normalized positions kx/π,ky/πand kz/π)for(a)Ω1=Ω2=Ω3=3.5γ1 and(b)Ω1=Ω2=Ω3=3γ1 with kj=κ(j=1–6)andθ=η=ξ=0,(c)θ=η=ξ=π/16 and(d)θ=η=ξ=π/8 withΩ1=Ω2=Ω3=3γ1,k1=k3=k5=0.6κ,k2=k4=k6=κ.The other parameters from(a)–(d)are the same as those in Fig.2.

Now we discuss the effect of phase shifts of the relevant fields on atom localization.In the case of k1=k3=k5=0.6κ,k2=k4=k6=κandθ=η=ξ=π/16(see Fig.4(c))we find that 16 small spheres convert to 2,which shows precision enhancement up to 80%.Now by further settingθ=η=ξ=π/8(see Fig.4(d))we clearly see that a single precise sphere appears in 3D volume space.This implies that the probability of locating an atom in a single period of SWFs is improved to 100%percent.

3.4.The fourth case:Ωs=0

In this subsection,we show our results for localization of an atom in 3D volume space by choosingΩs=0 in Eq.(10)and see how localization is achieved.It is important to understand the physics before going to discuss atom localization.When we setΩs=0,this decouples|4〉from tripod system and restores to an ordinaryΛ-type atomic system in EIT.Under semi-classical dress picture,upper level will split to two dress states|±〉.This splitting shows two windows corresponding to level|2〉↔|±〉.Hence,our system is still in DEIT condition.

Now we are going to discuss 3D atom localization under the conditionΩs=0 in Eq.(10).We take Imχp=0.9 of Eq.(10)and see 3D atom localization.Here,we follow the same procedure as we discuss in Subsections 3.1,3.2 and 3.3,respectively.First,we see the influence of control field intensity on atom localization and show that atom localization is highly sensitive to the field intensity.Under the case ofΩs=0,Ω1=Ω2=Ω3=3.5γ1,kj=κ(j=1–6)and θ=η=ξ=0,we see 16 big sphere-like structures spreading in different sub-spaces of 3D volume space,as shown in Fig.5(a).This indicates possible information about an atom in 3D volume space.For the caseΩ1=Ω2=Ω3=3γ1we notice that all big spheres become smaller,which shows precision enhancement as shown in Fig.5(b).From these findings it is clearly understood that the intensity of the control field has a significant effect of 3D atom localization.

We are now going to address the impact of phase changes of the related fields on atom localization.When we set k1=k3=k5=0.8κ,k2=k4=k6=κandθ=η=ξ=π/4(see Fig.5(c))we notice that 16 small spheres convert to 2,showing a precision improvement of up to 80%in 3D volume space.Now by further changingθ=η=ξ=π/8(see Fig.5(d))we clearly see a single precise sphere in 3D volume space.This means that by setting system parameters a 100% probability of detecting an atom in 3D volume space is achieved.

Fig.5.Plots for the probe absorption(Imχp=0.9)versus normalized positions kx/π,ky/πand kz/π)atΩs=0 for(a)Ω1=Ω2=Ω3=3.5γ1 and(b)Ω1=Ω2=Ω3=3γ1 with k j=κ(j=1–6)andθ=η=ξ=0,(c)θ=η=ξ=π/4 and(d)θ=η=ξ=π/8 withΩ1=Ω2=Ω3=3γ1,k1=k3=k5=0.8κ,k2=k4=k6=κ.The other parameters from(a)–(d)are the same as those in Fig.2.

3.5.The fifth case:Signal field absorption spectrum

In this subsection,we use the signal-field absorption spectrum(Imχs)of Eq.(12)and plot our results versus normalized positions(kx/π,ky/π,and kz/π)and show how precise 3D atom localization is achieved by varying different system variables.

As we see the two EIT windows in Subsection 3.1 for the probe-field case,similarly we also observe two EIT windows for the signal-field absorption spectrum.The two weak fields(signal and probe)will propagate through the medium with group velocity lower than the speed of light and maintain the DEIT condition.

Now for atom localization we plot the imaginary part of signal field optical susceptibility(Imχs)that is related to the absorption coefficient of signal field,depending on the moving atom’s position as it passes through SWFs.Similar to all the above cases in Subsections 3.1,3.2,3.3,and 3.4,first we see the role of control field intensities on atom localization.We chooseΩs=0.2γ1,Ωp=0.3γ1,withΩ1=Ω2=Ω3=3.5γ1,kj=κ(j=1–6)andθ=η=ξ=0 in Fig.6(a).We observe that the absorption of the signal is distributed into volume space,showing 16 sphere-like structures with broad sizes.This shows the possible position information of an atom in volume space,whereas due to high size of each sphere the resolution is poor.Further,in the case ofΩ1=Ω2=Ω3=2.5γ1,as in Fig.6(b),we clearly see that the volume of each sphere becomes smaller,which shows precision enhancement.From these findings it is apparent that position of an atom depends on the strength of the control field.Our next task is now to obtain a single precise position on an atom with high spatial resolution in 3D space.

Here we follow the same approach as in the previous sections(Subsections 3.1,3.2,3.3,and 3.4)and see the impact of phase changes of the related fields on atom localization.When we choose k1=k3=k5=0.85κ,k2=k4=k6=κandθ=η=ξ=π/4(see Fig.6(c))we notice that 16 spheres change to 5 small spheres,showing a precision improvement in 3D volume space.Now by further changingθ=η=ξ=π/3(see Fig.6(d))we clearly see a single precision sphere in 3D volume space.This implies that a 100% probability of detecting an atom in 3D volume space is obtained by properly adjusting the system parameters.

Fig.6.Plots for the signal field absorption spectrum(Imχs)versus normalized positions(kx/π,ky/πand kz/π)atΩs=0.2γ1,Ωp=0.3γ1,ηs=1 for(a)Ω1=Ω2=Ω3=3.5γ1 and(b)Ω1=Ω2=Ω3=2.5γ1 with kj=κ(j=1–6)andθ=η=ξ=0,(c)θ=η=ξ=π/4 and(d)θ=η=ξ=π/3 withΩ1=Ω2=Ω3=2.5γ1,k1=k3=k5=0.85κ,k2=k4=k6=κ.The other parameters from(a)–(d)are the same as those in Fig.2.

4.Influence of Doppler broadening on 3D atom localization

In this section,we discuss the influence of Doppler broadening on 3D atom localization.When an atom is driven by a laser fields even though there is a possibility that the atom is not completely stationary.[48]One effect of moving atoms is detuning of resonant frequencies due to the Doppler shift,which results in a velocity-dependent probe-field susceptibilityχp.Now the frequency detunings of the probe,signal and control beams due to the Doppler shift will become ΔP→ΔP+kv,Δs→Δs+kv,andΔc→Δc+kv,[49]respectively.Here v is the velocity of the atom and k is the wavevector of the corresponding fields.We replace these new frequency detunings in Eq.(10).Thus,in the presence of Doppler effect,we rewrite the Maxwell–Boltzmann velocity distribution equation for imaginary part of optical susceptibility¯χpfor 3D atom localization as

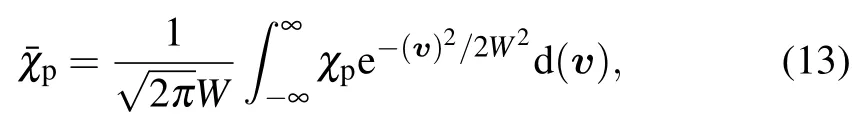
In Fig.7,we plot the Doppler-broadened 3D filter function of Eq.(13)versus the normalized positions kx/π,ky/π and kz/πfor different Doppler width(W)values,i.e.,W equal to(a)0.5γ1,(b)1γ1,(c)1.5γ1and(d)2γ1while keeping the other parameters as same as those in Fig.2(d).For W=0.5γ1,we see that the single precise sphere that appears in Fig.2(d)is growing,which means that the precision of the position of the atom has been diminished as shown in Fig.7(a).As we change W=1γ1,we see in Fig.7(b)that the three small spheres begin to appear,which are not present without Doppler-broadening and cause a reduced probability.Under the condition of W=1.5γ1in Fig.7(c)the three small spheres become larger with one extra small sphere,dramatically demonstrating that the resolution of the atom position has become lower.Now we increase the value of the Doppler width W=2γ1,as a result the all five spheres have been converted into very wide and broad spheres as shown in Fig.7(d).Therefore,it is observed that the precision of the atom’s position in 3D volume space is reduced and that accurate information of the atom position can not be presented when the Doppler effect is introduced in the calculation.

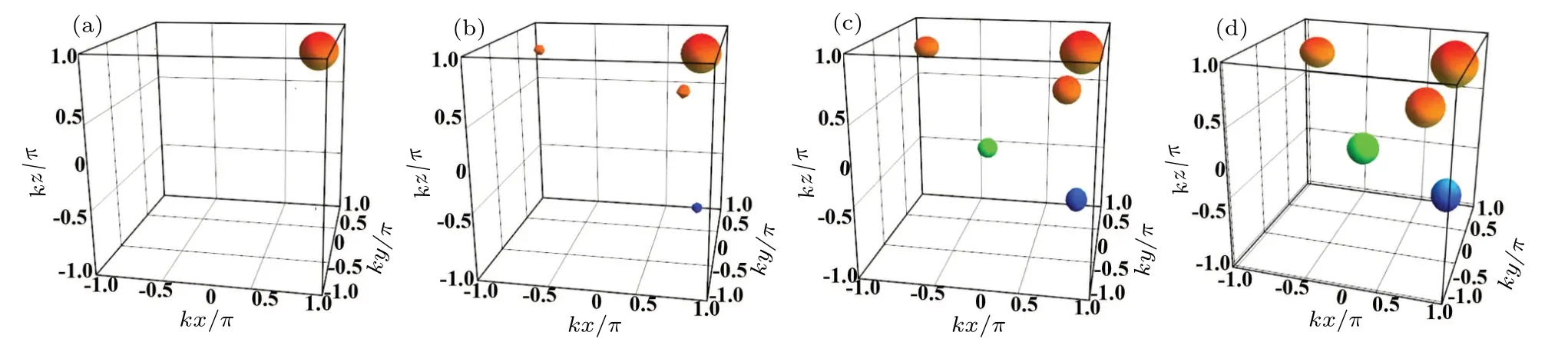
Fig.7.Plot of Eq.(13)Im¯χp for different values of the Doppler width W against the normalized positions(kx/π,ky/πand kz/π).Doppler width W:(a)W=0.5γ1,(b)W=1γ1,(c)W=1.5γ1,(d)W=2γ1.The remaining variables are the same as those in Fig.2(d).

5.Possible experimental realization

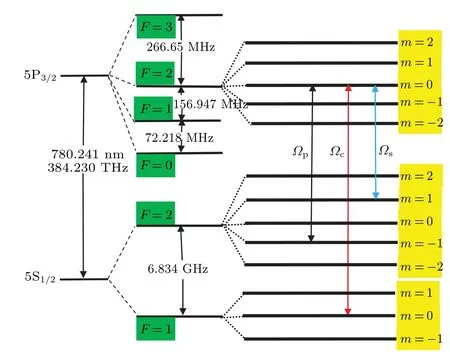
Fig.8.Possible experimental realization scheme for a four-level 87Rb atomic system.

6.Conclusion

In conclusion,different from the current localization schemes,[40–44,46,47]we have investigated a new scheme to achieve high-efficiency and high-spatial 3D atom microscopy by measuring DEIT in a four-level tripod atomic system.Owing to the spatially dependent atom field interaction,the precision position information of the single atom in 3D volume space can be determined through DEIT.It is explicitly shown that the maximum detecting probability of an atom can reach 100% in 3D volume space by properly varying system variables.The major advantage of the current scheme is that the conditional position probability distribution of the atom is improved to a factor of 4 or 8 as opposed to the previously suggested schemes.[40]

We also see the impact of the Doppler shift on 3D atom localization.We show that the Doppler shift significantly affects the precision of spatial information of an atom.Hence,our scheme is experimentally viable for ultra-cold atoms because it is based on the absorption spectrum and not spontaneous emission spectrum which is hard to control.Hence,our proposed scheme will be useful in several quantum applications such as optical imaging,laser cooling and atom nanolithography.

Acknowledgement

The author Abdul Wahab gratefully acknowledges the support from the CAS-TWAS for his Ph.D.study at University of Science and Technology China,in the category of 2018 CAS-TWAS President’s Fellowship Awardee(Grant No.CAS-TWAS 2018-37).