Terahertz radiation generation by beating of two chirped laser pulses in a warm collisional magnetized plasma

Motahareh Arefnia,Mehdi Sharifian,and Mohammad Ghorbanalilu

1Department of Physics,Shahid Beheshti University,1983963113,Tehran,Iran

2Physics Department,Yazd University,Safaiyeh,Yazd,Iran

Keywords:plasma,THz radiation,thermal effect,collisional effect,frequency chirp

1.Introduction

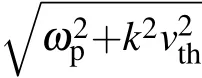
In the course of this paper,we study THz generation from the chirped lasers beating in a magnetized rippled density plasma by considering collisional frequency and thermal velocity.The static magnetic field applied perpendicular to the direction of the propagation of the beating lasers.The plasma density is periodically changed with wave numberαwhere the periodic plasma density helps to get phase-matching condition and resonant excitation in the THz frequency range.The laser pulses exert the transverse ponderomotive force to the electrons which produces the nonlinear current and finally THz radiation.This paper aims to investigate the effect of frequency chirp on the amplitude of THz radiation in the plasma density ripple which is affected by thermal effects,temperaturedependent collisions,and external magnetic field.

This paper is organized as follows:in Section 2,the nonlinear current density produced by beating chirped laser pulses is obtained.Then the THz field amplitude is analyzed by calculation of the dielectric permittivity tensor in warm collisional plasma.In Section 3,we examine the numerical results.In Section 4,the conclusion is presented.

2.Theoretical consideration

We consider two Gaussian lasers of same intensity(I～1014W/cm2),frequency chirpωjand wavenumber kj(where j=1,2)are propagating across(in the x direction)the magnetic field in z direction.The laser beams produce spaceperiodically density n=n0+n where n=nαeiαx,n0is uniform plasma density and nαis amplitude of the ripple.The electric field for laser pulses are given by

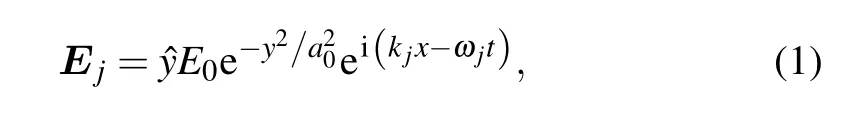
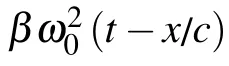
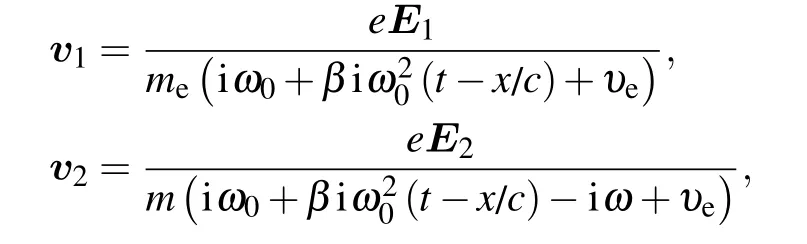
whereυeis the total electron collision frequency including electron–ion and electron–neutral frequencies and written in the form asυe=υen+υei.The electron ion frequency generally depends on ion density ni,the degree of the plasma ionization Zi,the electron temperature Te,and the Coulomb logarithm lnΛ.We choose lnΛ=10,and the electron–ion collision frequency is given as[40]

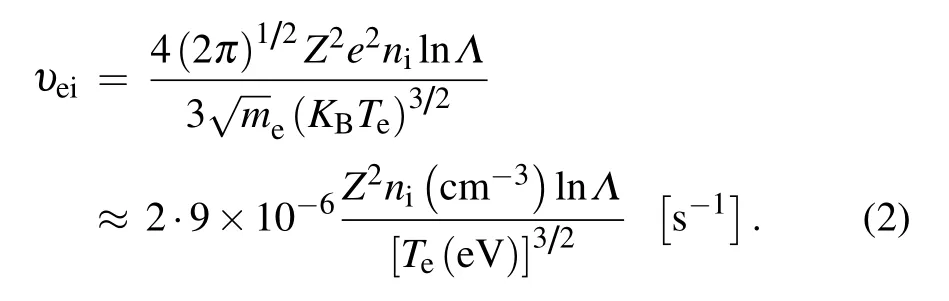
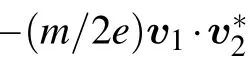
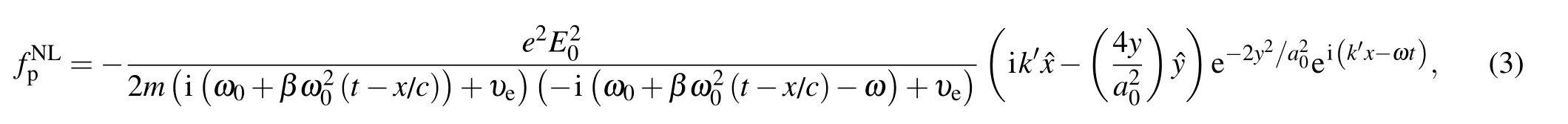
whereω=ω1−ω2and k′=k1−k2are beat frequency and wavenumber.

By making use of ponderomotive force the equation of motion in magnetized plasma is written as

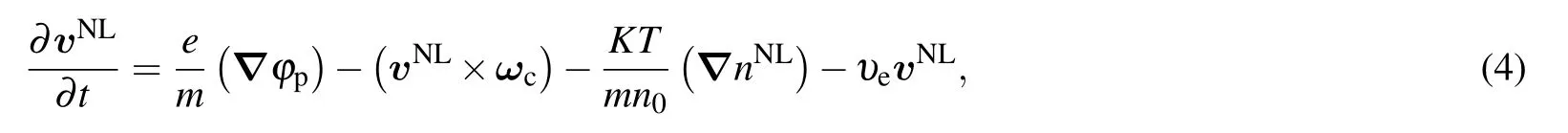
whereωc=(eB/mc)ˆz is the cyclotron frequency.The nonlinear electron density obeys the continuity equation(∂nNL/∂t)=−n0∇·vNL.

By solving Eq.(4)and making use Eq.(3)and nonlinear continuity equation,the nonlinear density perturbation is obtained as

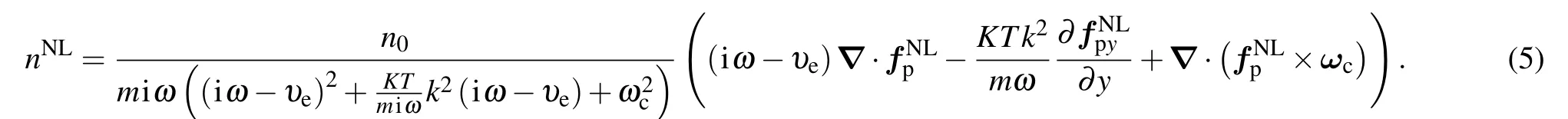
The nonlinear perturbations are affected by ponderomotive force,magnetic field,collisional force,and thermal quiver velocity.Therefore,the space charge field(corresponding potentialφ)is generated and then the linear density perturbations is induced,which is given by

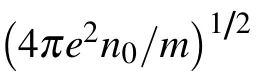
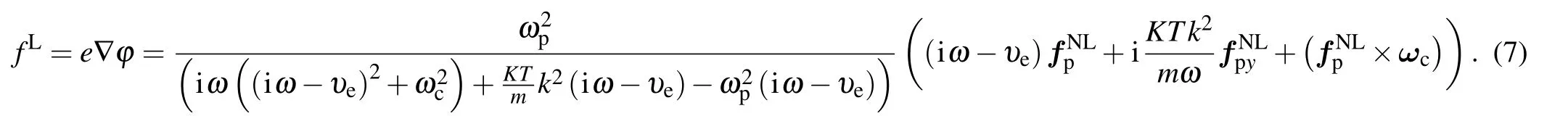
Therefore,the nonlinear velocity components are obtained by using Eq.(4)as

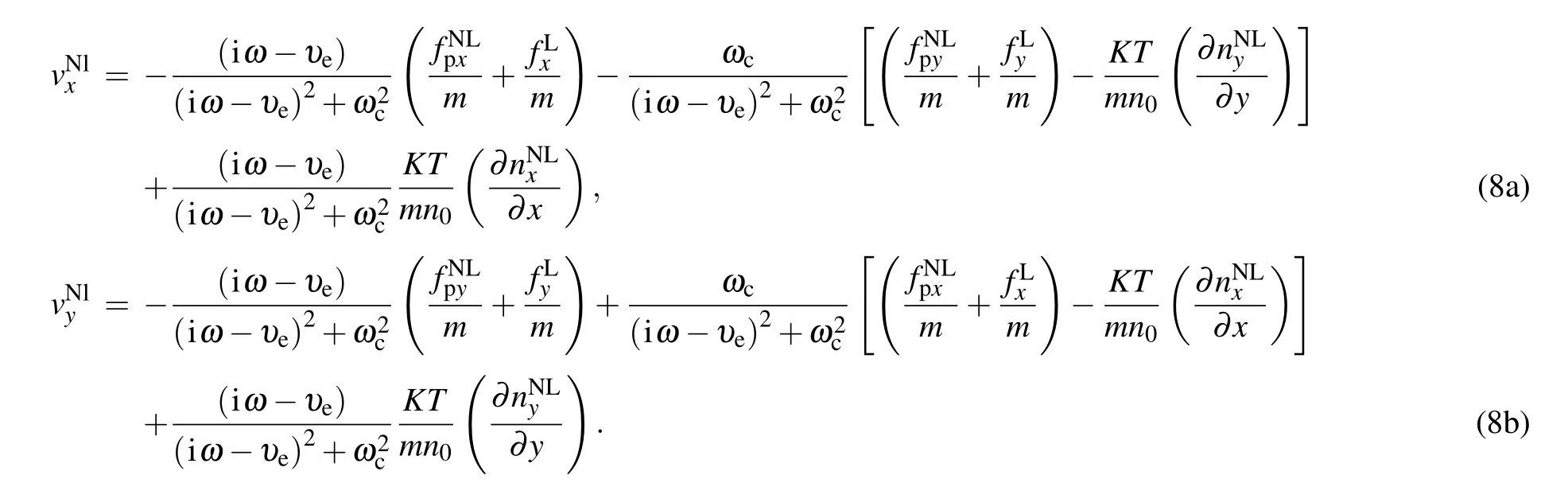
Now,the nonlinear current density is obtained by JNL=−(1/2)n′evNL.It is clear that the nonlinear current is modified by external magnetic field,thermal velocity,nonlinear ponderomotive force,and the linear force due to the self-consistent spacecharge field.

The complete form of nonlinear current density components is written in the form as

where

and k≡k′+α=k1−k2+αis wavenumber of THz oscillation.We know the nonlinear current responsible for the emission of THz radiation.

The wave equation of THz radiation is obtained by using the Maxwell’s equation and can be written as

By substituting dielectric tensor Eq.(12)in the wave equation of Eq.(11),the wave equation is obtained as

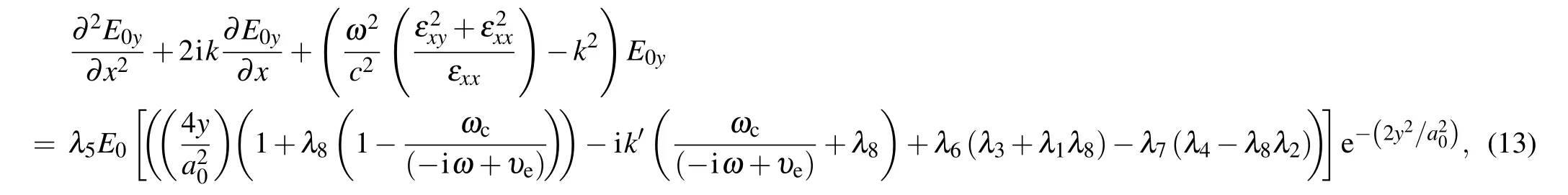
where

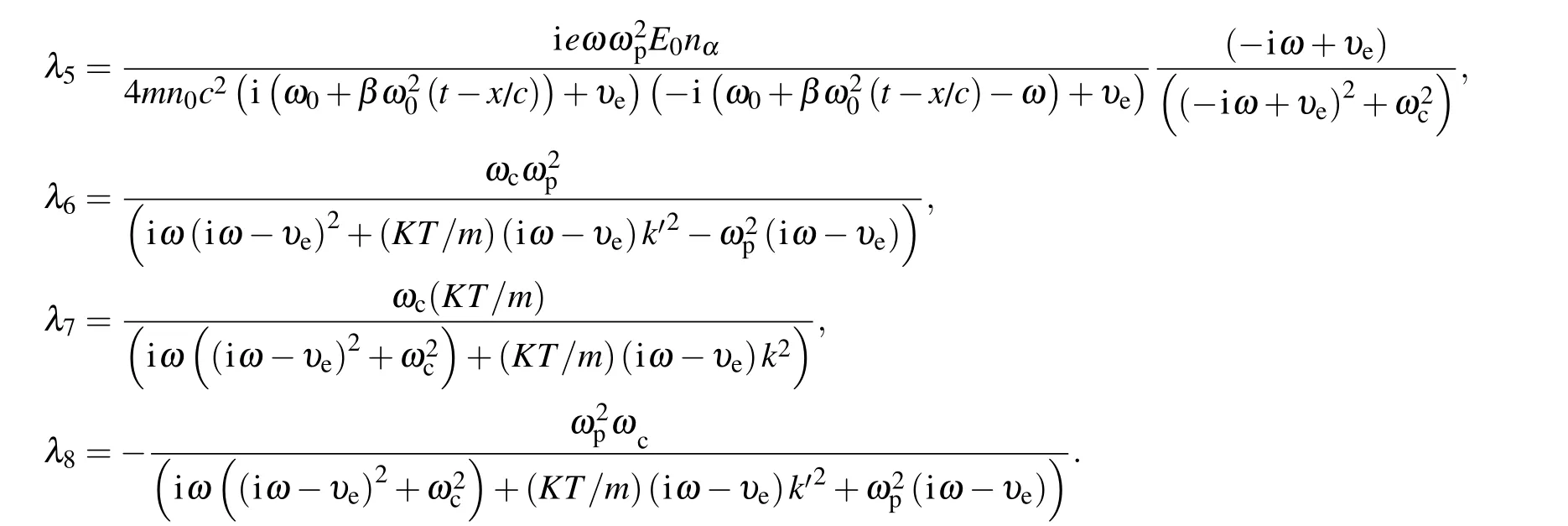
Following the phase matching condition in rippled density plasma we use

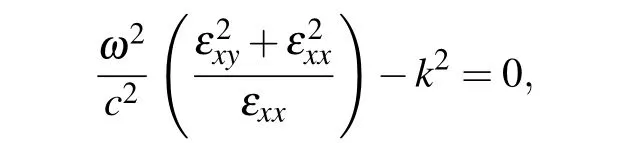
and obtain the normalized THz radiation field as

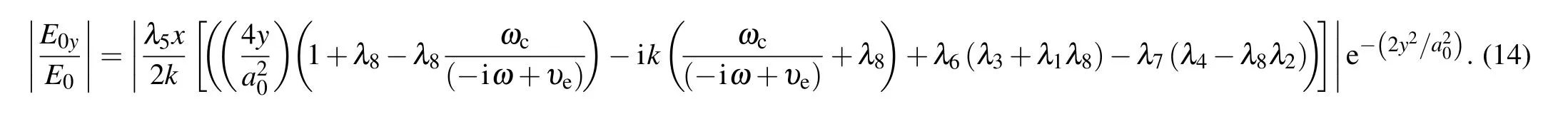
3.Results and discussion

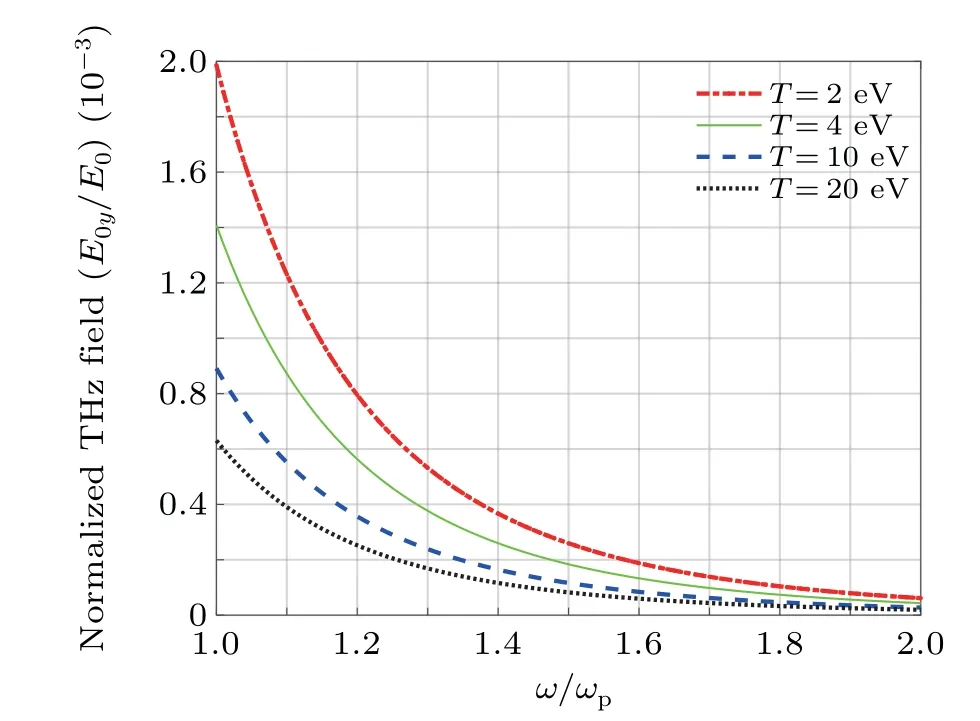
Fig.1.Normalized amplitude of THz radiation feild as a function /of normalized beat frequency for different values of temperature whenωcωp=0.1 andβ=2.

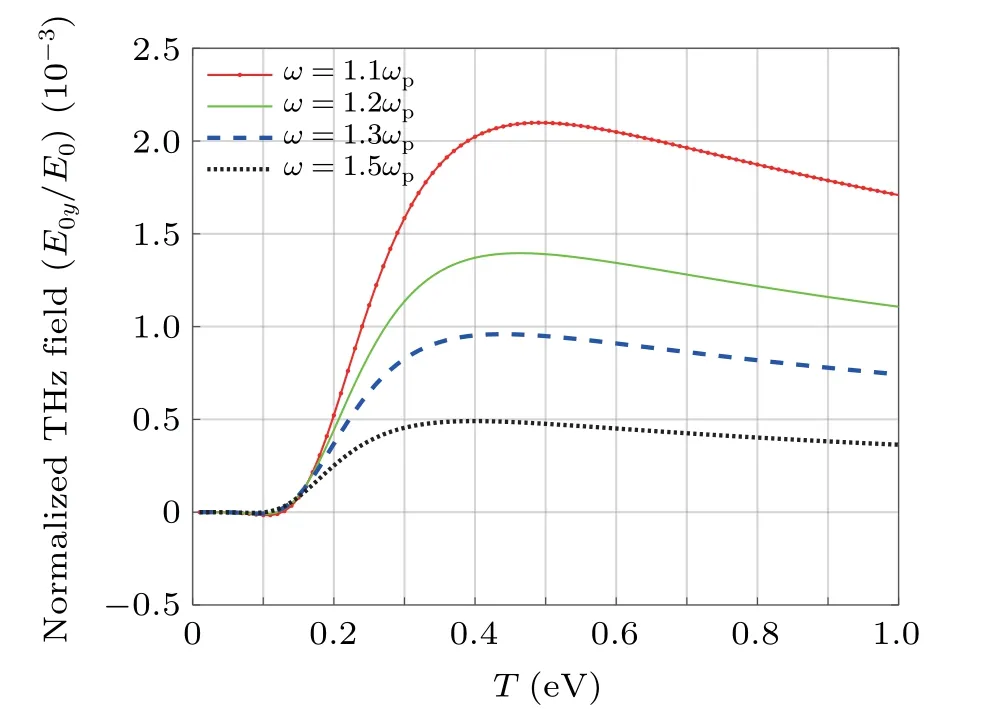
Fig.2.Normalized amplitude of THz radiation field as a function of temperature for different values of normalized beat frequency.The parameters are the same as those in Fig.1.

In Fig.3,we plotted the radiation field amplitude on beat frequency for different values of frequency chirp parameters.We see that for different chirp parameters the maximum amplitude of the THz field accrues still as the beating frequency ωapproaches to plasma frequencyωp,so that the gradient of the curve is sharper for the smaller chirp parameter.The THz field amplitude increases by applying the appropriate chirp parameter where the interaction of beating wave and plasma becomes more effective.The THz field amplitude variation with respect to frequency chirp parameter for different normalized cyclotron frequencies is plotted in Fig.4.The figure shows that the normalized THz field amplitude increases by decreasing positive chirp and it is more noticeable when the higher magnetic field is applied.The presence of magnetic field helps to tune the frequency and amplitude of the emitted THz.The behaver of curves is in good agreement with three-dimensional(3D)simulation results of Nguyen et al.[41]

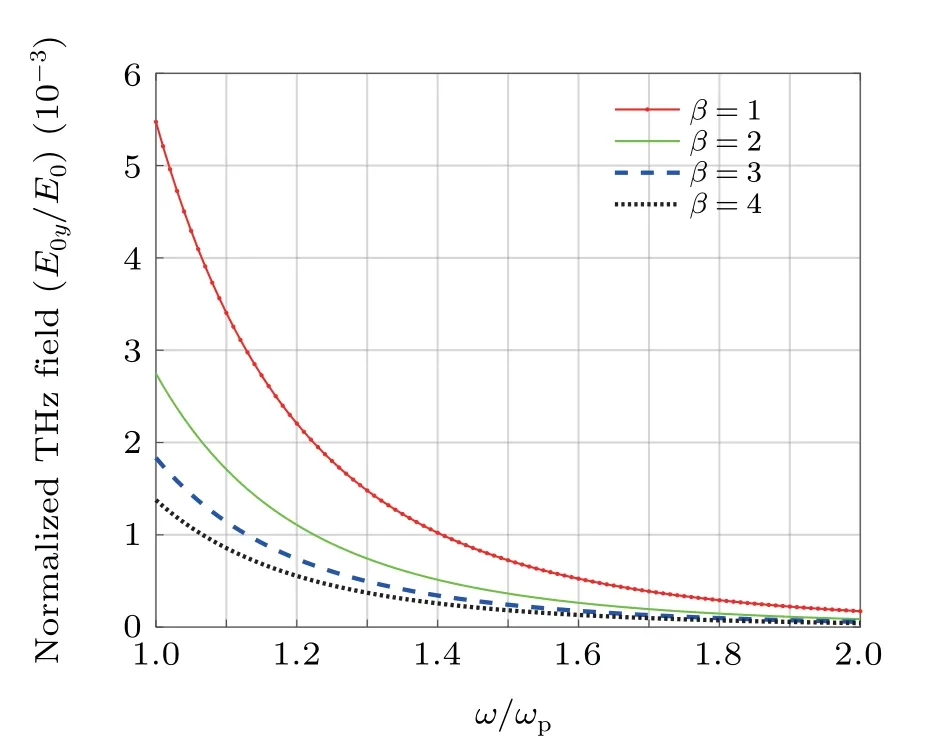
Fig.3.Variation of normalized amplitude THz radiation field with normalized beat frequency for different values of frequency chirp parameter when ωc/ωp=0.1,T=1 eV.

Fig.4.Variation of normalized amplitude of THz radiation field with frequency chirp parameter for different values of normalized electron cyclotron frequency whenω/ωp=1.1,T=1 eV.

Figure 5 depicted the THz amplitude as a function ofβ for different values of temperature.It is lucid that the influence of the frequency chirp parameter is dominant for lower temperatures.At the lower temperatures the electron collision frequency is increased and tuned with the frequency chirp.

Fig.5.Normalized amplitude of THz radiation field as a function of frequency/ chirp parameter for different values of temperature whenωc/ωp=0.1,ω ωp=1.1.

In Fig.6 we analyze the variation of THz amplitude as a function of temperature for different values of negativeβ.It is clear that,the THz field attains a peak at a particular value of T.In this region the optimum temperature increases at higher|β|.Figure 7 shows the dependent of the THz field amplitude on beat frequency and chirp parameter at temperature 0.1 eV.Here,it is observed that a peak appears for the THz field in a value of negative chirp parameterβ≈−0.008.In Fig.8 we show the variation of THz amplitude with the temperature and frequency chirp parameter.We find that the THz field amplitude is maximized at the specific negative frequency chirp parameter,so that by increasing the temperature and consequently closer to the resonant excitation the optimum frequency chirp becomes more effective.

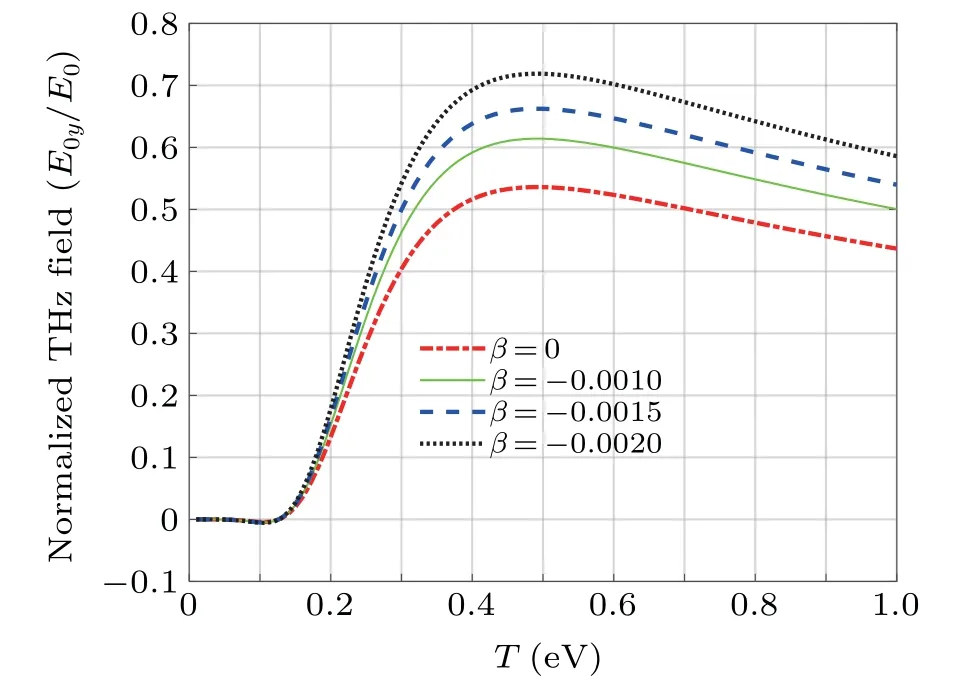
Fig.6.Normalized amplitude of THz radiation field as a function of temperature for different values of frequency chirp parameter when the parameters are the same as those in Fig.5.

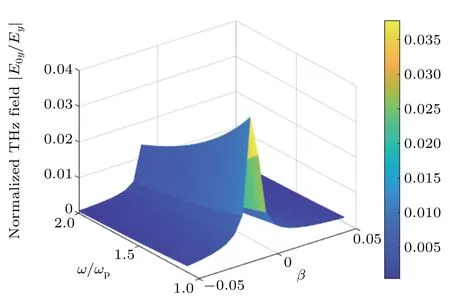
Fig.7.Spatial normalized amplitude of THz radiation field as a function of normalized beat frequency and frequency chirp parameter forωc/ωp=0.1,T=0.1 eV.

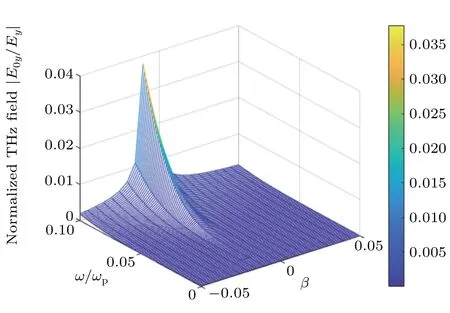
Fig.8.Spatial normalized amplitude of THz radiation field as a function of temperature and frequency chirp parameter forω/ωp=1.1,ωc/ωp=0.1.

4.Conclusion