Ferromagnetic Heisenberg spin chain in a resonator

Yusong Cao(曹雨松),Junpeng Cao(曹俊鹏),and Heng Fan(范桁)

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

3Songshan Lake Materials Laboratory,Dongguan 523808,China

4Peng Huanwu Center for Fundamental Theory,Xi’an 710127,China

5CAS Center for Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100190,China

Keywords:magnon,resonator,quantum phase transition

1.Introduction

Rabi model plays an important role in various fields in physics.The physical setup of the Rabi model is very simple:a two-level atom with magnetic momentum and electrical dipole momentum in an electromagnetic resonator.[1]One of the reasons that Rabi model draws so much attention is the rich experimental realizations of the two-level systems such as the quantum qubit in quantum computation.[2–6]Rabi model also plays an important role in the semiconductor physics[7]and the ion-trap technology.[8]In the quantum technology,especially the quantum information and quantum computation,we need many two-level systems to serve as quantum gates to perform quantum computing.One of the associated models is the Dicke model which is a generalization of Rabi model.[9]The Dicke model describes N free two-level atoms interacting with the cavity field.We should note that the behavior of the photon field is also worth studying.The most representative example is the superradiant phase transition of the cavity field obtained from the thermodynamical limit of the Dicke model.This kind of phase transition belongs to the quantum phase transition.[10–16]

Recently,the application of Rabi model and generalized Rabi models in the condensed matter physics causes renewed interests and has been studied extensively.[17–21]The typical Rabi-type model is the Rabi–Hubbard model,where the twolevel atom is replaced by a Hubbard lattice.

When the two-level systems are used to simulate the quantum qubits in the cavity QED experiments,the decoherence of the qubit systems is a major problem which may cause the trouble in building the quantum gates.In order to overcome this difficulty,one possible scheme is to search for different carriers of quantum qubits such as the superconductor qubits,annoys qubits,and magnon qubits in the ferromagnets.[22–29]

In this paper,we consider the ferromagnetic Heisenberg spin chain in a resonator.The system is obtained by replacing the two-level atom in the Rabi model by the spin chain with ferromagnetic isotropic nearest neighbor exchanging interactions.The elementary excitation of the spin chain is the magnon.The magnons interact with the electromagnetic field in the resonator.We find that the dynamical behavior of the system can be divided into four regimes,i.e.,decoupling regime,Jaynes–Cummings(JC)regime,two-fold dispersive regime,and ultra-strong coupling regime,based on the oscillation frequencies of different interaction terms.We obtain the energy spectrum of the ground state and low excited states of the system.If the magnons and cavity field modes are in resonance,we obtain the analytical solution of the system.Near the resonance point where the detuning is very small,we study the system with the perturbation theory.We also discuss the symmetry broken of the system.We find that the cavity field exhibits a quantum phase transition.The corresponding critical exponent from normal phase is given.

This paper is organized as follows.We introduce the Hamiltonian of the system in Section 2.In Section 3,we compute the energy spectrum at the ground state and the low excited states in different regimes of model parameters by using the different methods such as exact solution,effective Hamiltonian,and perturbation theory.In Section 4,we discuss the symmetry broken of the system and give the critical exponent of the quantum phase transition.The main results are summarized in Section 5.

2.Model Hamiltonian

The model considered in this paper contains three parts:(a)a spin chain with ferromagnetic isotropic nearest neighbor interaction,(b)a resonator with electromagnetic field,and(c)interaction between the spin chain and the electromagnetic field.The model Hamiltonian reads Hm=HFM+HEM+Hint.Here the HFMdenotes the Hamiltonian of the ferromagnetic Heisenberg spin chain

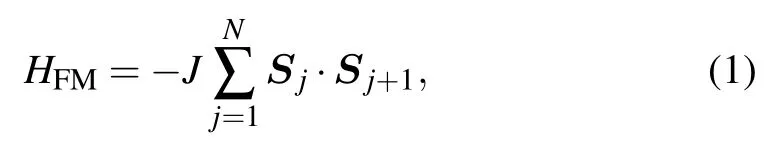
where J is the coupling constant,N is the number of sites,and Sjis the spin-S operator at site j.We consider the periodic boundary condition thus SN+1=S1.The term HEMstands for the Hamiltonian of the electromagnetic field in the resonator

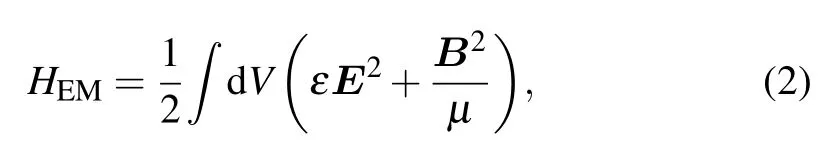
whereεis the electrical conductivity,µis the magnetic conductivity,and E and B are the strengths of electric field and magnetic field,respectively.The term Hintis resulted from the interaction between the spins and the magnetic field in the resonator

where g is the coupling constant and xjis the position of the j-th spin.

In order to see the collective behavior of the spin chain more clearly,we write the Hamiltonian Hmin the momentum representation.With the help of Holstein–Primakoff transformation,if the spin S is large enough and the chain is in the low excited states,the Hamiltonian of the spin chain(¯h=1)reads

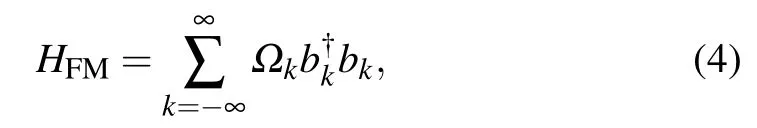
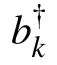
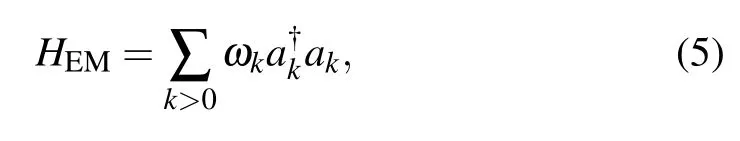
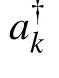
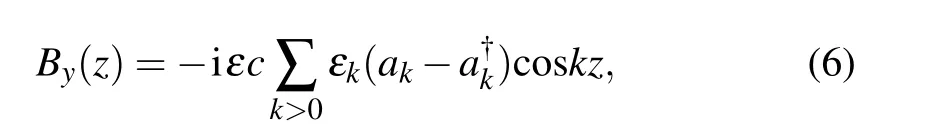
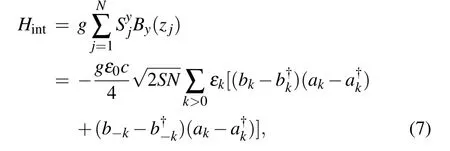
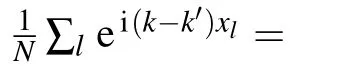
Next,we write the full Hamiltonian as Hm=H1+H2,where

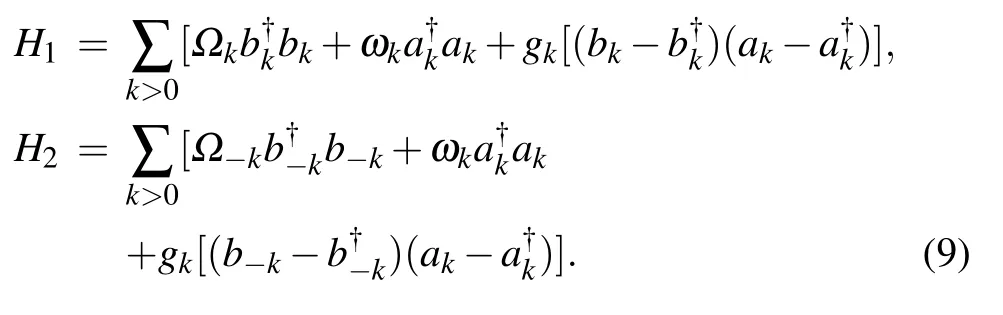
From Eq.(9),we know that the Hamiltonian H1is blocked in momentum space,i.e.,H1=∑kH1,k,because the magnon with wave vector k only interacts with the photon of mode k.The explicit form of H1,kreads

We should note that the Hamiltonian H1acts only on the Hilbert space with magnon vector k>0.In the Hamiltonian H2,the magnon with wave vector−k only interacts with the photon of mode k.Thus H2acts on the Hilbert space with magnon wave vector k<0.In the experiment settings,we could use external methods to modulate the magnons.For example,by putting a spin wave valve on the spin chain,we can get rid of all the magnons with wave vector k<0,which allows us to eliminate the term H2and only consider the Hamiltonian H1.

We concentrate on the Hamiltonian H1,k.Omitting the subscripts,we arrive at

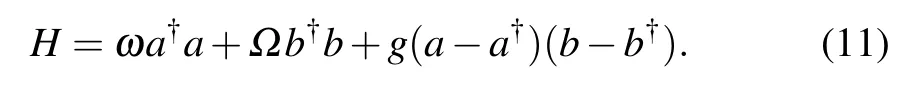
For the later using,we rewrite Hamiltonian(11)as H=H0+HI,where H0=ωa†a+Ωb†b denotes the non-interacting parts and HI=g(a−a†)(b−b†)means the interaction terms.Comparing with the standard Rabi model,we find that the HIcan also be rewritten as

where Hr=g(a†b+ab†)and Hcr=g(a†b†+ab)are the rotating wave and counter-rotating wave terms,respectively.

3.Dynamics and solutions

In order to study the dynamic behavior of the system(11),we first consider the interaction term HIin the interaction picture

From Eq.(13),we see that the rotating wave term and counterrotating wave term oscillate with different frequencies,which is similar to the case of Rabi model.[30]Because the different interaction terms oscillate with different frequencies,the oscillating terms with high frequencies can be neglected.From the detailed analysis of Eq.(13),we find that the dynamical behavior of the Hamiltonian(11)can be divided into following four regimes of model parameters:(i)decoupling regime where g≪ωand g≪Ω;(ii)JC regime where g≪ω,g≪Ωand|ω−Ω|≪|ω+Ω|;(iii)two-fold dispersive regime where g<ω,g<Ω,g<|ω−Ω|and g<|ω+Ω|;(iv)ultra-strong coupling regime where g>ωand g>Ω.

We shall note that the dynamical properties of Hamiltonian(11)and those of Rabi model[30]are different.First,in the Hamiltonian(11),there is no electrical dipole momentum.It is the magnetic momentum interacting with the magnetic field,which induces both the rotating wave and the counterrotating terms.The Zeeman term in the Rabi model is replaced by the kinetic energy term of the magnons.Second,the rotating wave and counter-rotating wave terms in the Hamiltonian(11)always have opposite signs.Third,in the present system(11),there does not exist the anti-JC regime of the Rabi model because the constraint|ω−Ω|>|ω+Ω|of anti-JC regime cannot be achieved by the present requirementsω>0 andΩ>0.

In the following subsections,we solve the eigen-energy spectrum of system(11).We focus on the later three regimes because there is no interaction in the decoupling regime and the corresponding results are direct.

3.1.JC regime

In the JC regime,the contour-rotating wave term can be neglected,i.e.,Hcr=0.Then the particle number operator ˆN=a†a+b†b of the system is conserved.This means that the Hamiltonian(11)is blocked as H=⊕nHn,where n is the particle number that is the eiegenvaue ofˆN and Hnis a(n+1)×(n+1)matrix with the form of

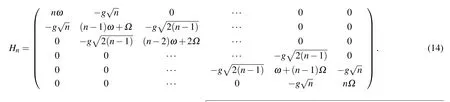
We see that the Hnis a tridiagonal matric which can be diagonalized numerically for arbitrary particle number n.If the particle number n is small,we can obtain the analytical results.

The Hamiltonian(11)in the JC regime reads H=H0+Hr,where H0is diagonal.Thus if the coupling constant g in Hris small,we can also solve the H by using the perturbation theory.In Fig.1,we show the energy spectrum of Hamiltonian(11)at the ground state and the first two excited states as the functions of g.The dots are the results obtained by the exact diagonalization of the Hamiltonian(11),while the solid lines are those obtained by using the perturbation theory up to the second order.We see that they are consistent with each other very well if the coupling strength g is small.This result is in agreement with that the perturbation theory is more accurate when the perturbation parameter is small.From Eq.(14),we see that the first two excited state energies can also be obtained by diagonalizing the matrix(14)in the subspace with n=1.The results are shown in Fig.2,where the dots are the energy spectrum at the ground state and the first two excited states obtained by exact diagonalization of the blocked Hamiltonian(14)and the lines denotes the corresponding results obtained by using the perturbation theory.Again,they are consistent with each other very well if the coupling strength g is small.

Fig.1.The energy spectrum of the system(11)in the JC regime at the ground state and the first two excited states as the functions of g.The dots are the results obtained by the exact diagonalization of the Hamiltonian(11),while the solid lines are those obtained by using the perturbation theory.We see that they are consistent with each other very well if the coupling strength g is small.Hereω=1 andΩ=1.3.In the simulation,the dimensions of operator a and b are 200×200 and 10×10,respectively.

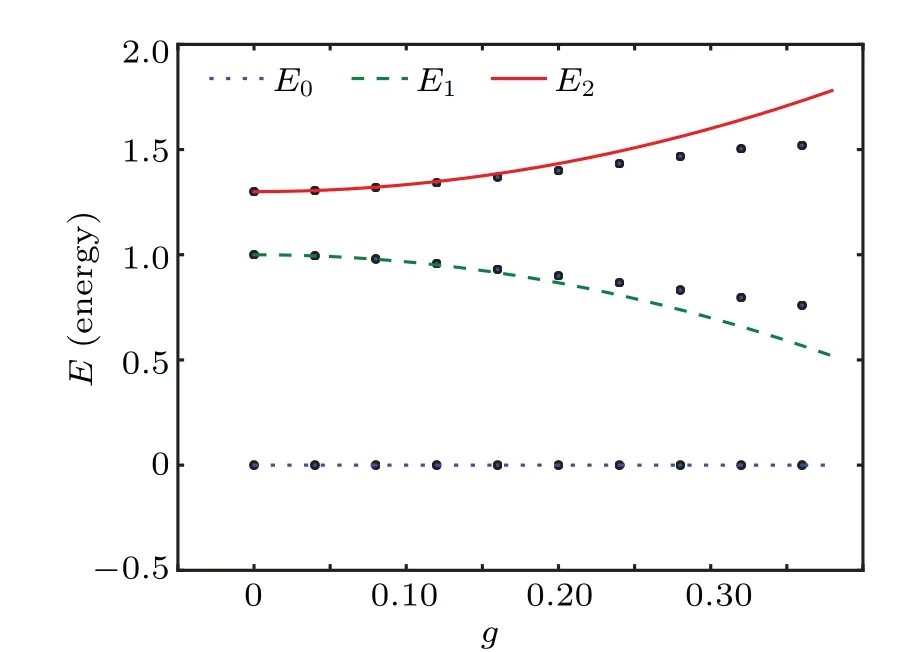
Fig.2.The energy spectrum of the system at the ground state and the first two excited states in JC regime as the functions of g.The dots are the results obtained from the diagonalization of block Hamiltonian(14)with n=0,1.The solid lines are the results obtained from the perturbation theory.We have setω=1 andΩ=1.3.

3.2.Two-fold dispersive regime

In the most experiments,the tunable parameters are in the two-fold dispersive regime.Since there is no analytic solution in this regime,we should solve the Hamiltonian with the help of numerical or approximation methods.From the above analysis,we know that the coupling strength g in this regime is small,which means that we can study the second order effective Hamiltonian just like the case in Rabi model.[31]In the language of scattering theory,the particle numbers of both photon and magnon are conserved in the scattering process.In order to obtain the effective Hamiltonian,we examine the matric elements

where r is a positive integer,naand nbare the particle numbers of photon and magnon,respectively.We see that the relation r≥2 must hold if the matric element(15)is required to be non zero.Therefore,up to the second order of g,the effective Hamiltonian of the system reads

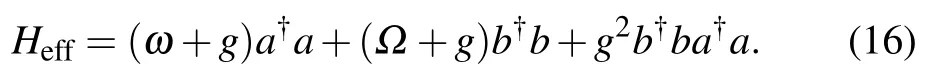
From Eq.(16),we see that the effective Hamiltonian Heffis a diagonal matrix and the diagonal elements in the particle number representation are the eigenvalues.

In Fig.3,we show the ground state and the first two excited states energies of the system obtained by using the exact diagonalization of the Hamiltonian and by the effective Hamiltonian method.We see that the results are consistent with each other when g is small.

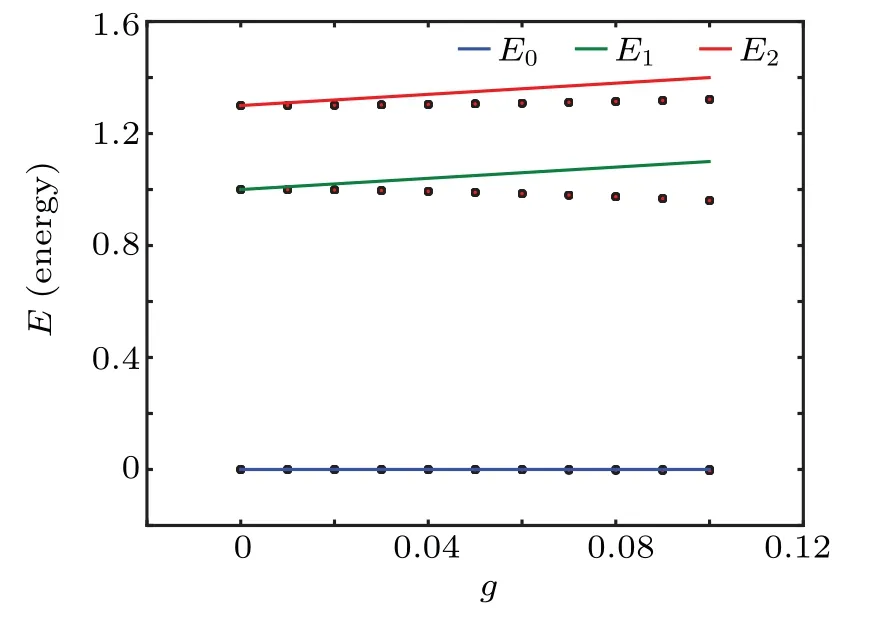
Fig.3.The energy spectrum for the ground state and the first two excited states in the two-fold dispersive regime.The dots are the results obtained from exact diagonalization of the Hamiltonian.The solid lines are the results obtained from the effective Hamiltonian.We have set ω=1 andΩ=1.3.

3.3.Ultra-strong coupling regime

3.3.1.Analytical point

In the ultra-strong coupling regime,the coupling constant g is large and we can not take the perturbation to g.We discuss the system in the resonance point ofω=Ω,where the Hamiltonian(11)reads

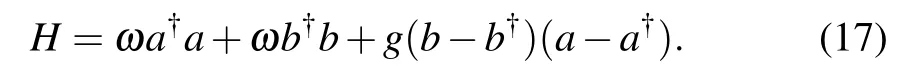
The Hamiltonian(17)is exactly solvable.Define the position-representations of the two sets of boson operators as

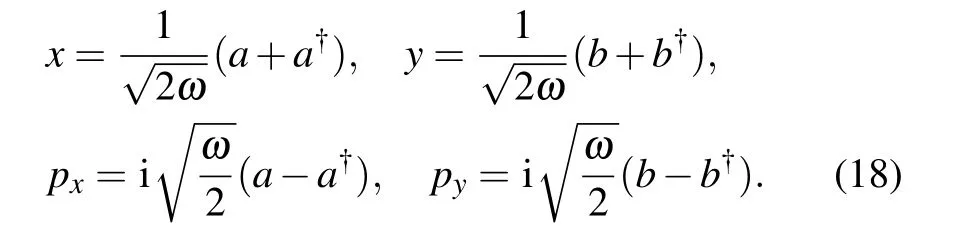
Then the Hamiltonian(17)becomes

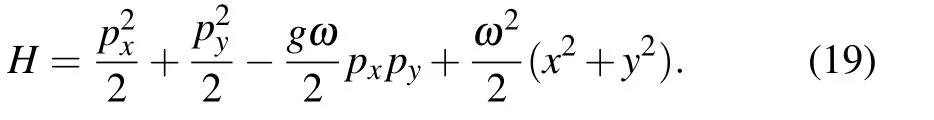
With the help of rotations of coordinate

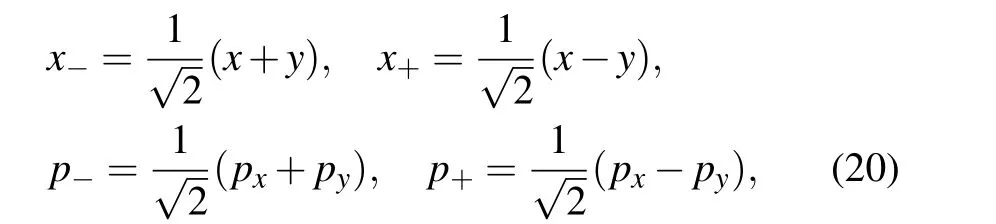
the Hamiltonian(19)turns into

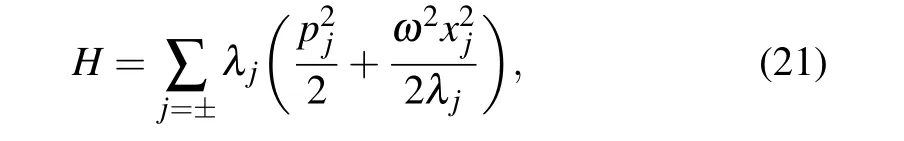
where

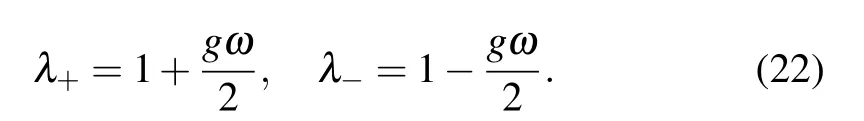
We define a new pair of creation and annihilation operators

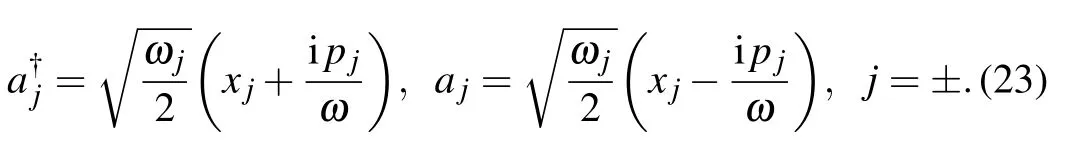
Then the energy spectrum of Hamiltonian(21)is

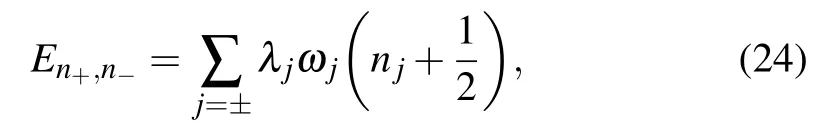
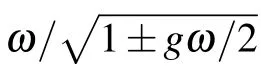
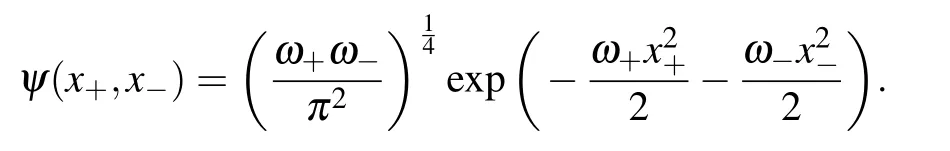
While if g>gl,the ground wave function is

Last,we should note that the above treatment method of resonance case is valid in all the regimes of model parameters.

Fig.4.The energy spectrum for the ground state and the first two excited states as the functions of g at the resonance pointω=Ω.We find that there exists a level crossing of energies at the ground state and the first excited state,resulting in the changing of parity of the ground state wave functions.We have setω=Ω=1.

3.3.2.Detuning

Next,we consider the regime near the resonance point.We define the detuning factorδasΩ=ω+δ.Then the Hamiltonian(11)reads

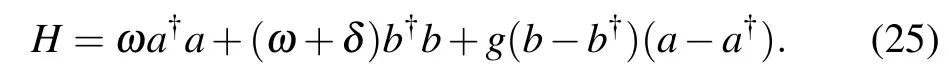
Substituting Eqs.(18),(20),and(23)into the above Hamiltonian,we arrive at

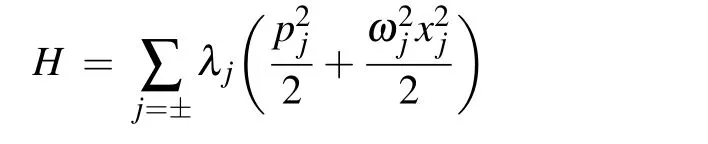
Rewrite the Hamiltonian(26)as H=Ha+Hp,where Hastands for the resonance Hamiltonian given by Eq.(17)and Hpstands for the extra terms as a result of detuning

Since Hahas been solved exactly and the detuning factorδis small,we can treat Hpas the perturbation.Up to the first order ofδ,the energy shifts of the first three eigen-energies of the Hamiltonian(26)are

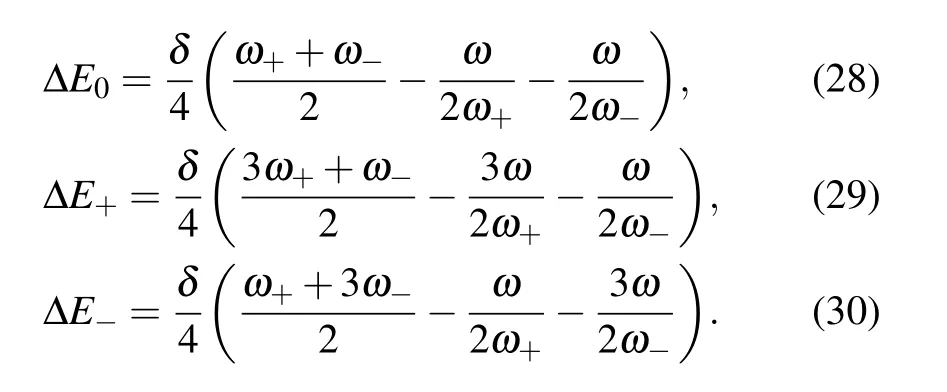
From Eq.(28),we see that the level crossing of the ground state and the first excited state takes place at

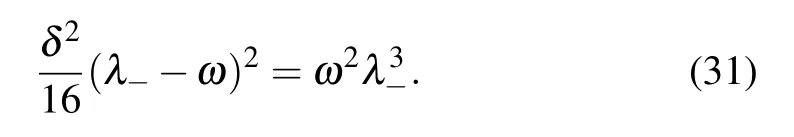
4.Symmetry-broken and quantum phase transition

The Hamiltonian(11)possesses the Z2symmetry induced by parity operator P=exp[iπ(a†a+b†b)].With the help of Baker–Housedorff equation,we have

Thus the Hamiltonian(11)can be divided into H=H(+)⊕H(−),where the superscripts are the quantum number of parity operator.In the resonance caseω=Ω,we have

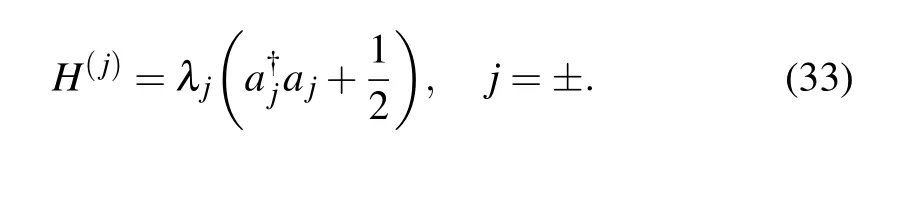
From Eq.(22),we know thatλ−vanishes at the point of gc=2/ω,which means that if g>gc,there does not exist the subspace with negative parity.The Z2symmetry is broken spontaneously,which results in the phase transition of the photon field.Near the critical point gc,the frequencyω−with negative parity is

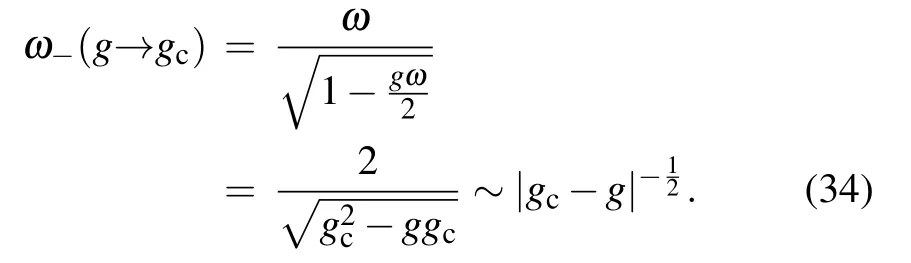
In order to obtain the critical exponent of the quantum phase transition,we apply the length scale method introduced in Ref.[16].The characteristic length scale of the system(11)in terms of energy is defined as

From Eq.(34),we know that the characteristic length l−divergences as|gc−g|−1/2,which gives the critical exponent as ν=−1/4.

5.Summary

In conclusion,we have studied the ferromagnetic Heisenberg spin chain in a resonator with spin wave valve.We find that the dynamical behavior of the system can be divided into four regimes according to the relation between the coupling strength and the frequencies of magnon and photon.We present the energy spectrum of the ground state and the first two excited sates in the JC and two-fold dispersive regimes.In the resonance case,we obtain the exact solutions of the system and the corresponding treatment method is universal,which can be applied to all the regimes of model parameters,especially in the ultra-strong coupling regime.Near the resonance point,we solve the system by using the perturbation method.Further,we analyze the spontaneous breaking of parity symmetry and study the critical exponent of quantum phase transition of the photon field from the normal phase.