基于射影变换的圆点标定板自动识别研究*

2021-09-28付生鹏赵吉宾夏仁波

组合机床与自动化加工技术 2021年9期

付生鹏，赵吉宾，夏仁波，李论

(1.中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016;2.中国科学院机器人与智能制造创新研究院，沈阳 110169)

0 引言

在计算机视觉应用中，需要首先要对视觉传感器也就是相机进行参数标定，以获得内部或者外部参数，以便进行后续的测量或检测任务[1]。因此如何快速而且准确的获得相机的参数，是使用计算机视觉技术首先要解决的问题。

张正友基于二维靶标的标定算法的提出，使得相机的参数标定过程变得方便和简单[2]，同时降低了标定靶标的加工难度，可以使用易于加工的二维靶标进行参数标定。常用的标定板有棋盘格、圆点标定板等多种形式[3-6]，其中圆点标定板由于加工方便、易于识别且精度较高，应用十分广泛。在进行图像识别时，需要识别出圆点中心并按照一定的顺序排列，从而与标定板上的点一一对应[7]。但是在标定板旋转角度较大或处于某些特定位置时，往往很难对圆点进行准确的排序，此时需要在标定板上设置一些特殊的标志进行辅助排序。例如，在标定板上设置编码标志点确定标定板的方向[8]，然而由于编码标志点识别的算法比较复杂，并且当距离较远时，通常无法准确识别编码点，这些都降低了标定板的识别率和准确性。

对于圆点标定板识别的问题，单宝华等[9]使用一角带有三角形图案的实心圆点标定板对双目相机进行了标定，能应对不同旋转角度的标定板识别问题，但是必须保证三角形角点在视野内才能实现；张琪等[10]设计了一种圆点标定板，该标定板一角有一个大圆，识别方法与前述方法类似，因此也存在同样的问题；夏仁波等[11]对包含两种大小标志圆的标定板识别展开了研究，由于圆点排序过程中仅基于对点图像距离和角度的计算，因此在某些极端情况下稳定性不佳；计算机视觉开源库opencv提供了一种无差别圆点标定板的识别方法，但是由于椭圆排布的对称性，无法做到多角度下的准确识别[12]。

本文提出了一种基于射影变换的圆点标定板自动识别方法，能够对一种包含两种大小标志圆点的二维标定板进行自动识别，并能根据大圆的图像坐标利用射影变换原理对所有圆点进行准确排序，从而建立标志点图像坐标与标定板三维坐标的一一对应关系。最后通过实验证明该方法能在较大角度范围实现标定板的自动识别，验证了方法的有效性。

1 标定板识别原理

1.1 标定板设计

本文所使用的标定板包含两种半径大小的圆形标志点，大圆半径约为小圆半径的2倍。所有标志点圆心之间的距离均一致，其中大圆用于确定标定板坐标系的位置和方向，其在标定板中具体位置可根据需要自由设定。如图1所示，以本文实验所用标定板为例，该标定板包含11×9个标志圆，其中大圆的半径约为小圆的直径的2倍，每个圆点中心距均为d=10 mm。5个大圆中，2和5距离最远，为6d，而3和4距离最近，距离为d，1和3之间的距离为4d。建立标定板坐标系如图所示，原点位于标定板中心圆上，Z轴垂直于标定板平面，此时5个大标志圆点在标定板坐标系下的三维坐标值分别为(-2d,0,0)，(0,-3d,0)，(2d,0,0)，(2d,d,0)，(0,3d,0)，其他圆点坐标值可以此类推。

图1 标定板示意图

1.2 射影变换原理

平面射影变换是射影平面上可逆齐次线性变换，其本身是一串变换的组合，变换层次较高。物体经过射影变换后与原形状相比将出现失真，如图2所示，点A、B、C、D位于π2平面上，点O为投影中心，点a、b、c、d为在平面π1相应的中心投影点，π1和π2之间为中心射影变换。射影变换不在具备保平行、保夹角等特性，但是保持直线、直线与点的结合性以及直线上点列的交比不变，因此也称为保线映射[13]。

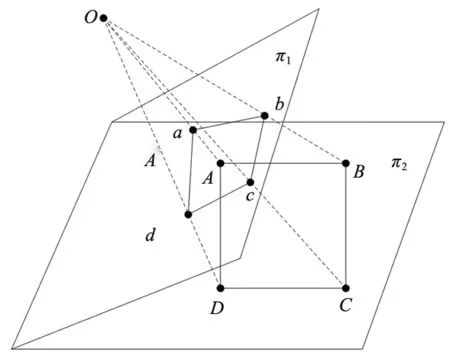
图2 射影变换

2 标定板识别算法

2.1 算法流程

标定板识别的目的是将标定板图像中的所有圆点按照一定的顺序提取出来并计算其圆心坐标值，这样就可以与已知的标定板实际坐标值相对应，方便后续的相机参数标定。标定板识别算法流程如下：

(1)首先对标定板图像进行预处理(颜色转换、滤波)，通过阈值分割和面积计算初步识别标定板候选区域；

(2)对所有标定板候选区域内的图像进行边缘提取并进行椭圆拟合，按照一定的规则进行过滤，识别候选区域内符合条件的圆形标志点，若区域内圆形标志点的个数大于等于m×n，此时可唯一确定标定板区域；

(3)根据直径和面积对所有椭圆进行排序，获得5个大标志圆，按照距离对5个大圆按照标约定的顺序进行排序；

(4)根据5个大圆圆心坐标和对应标定模板的圆心坐标计算射影变换矩阵，获取图像点与标定模板之间的射影变换矩阵；

(5)根据得到的射影变换矩阵，将标定模板内的所有圆点中心坐标投影到图像平面内；

(6)计算拟合得到的椭圆圆心与投影得到的圆心坐标值的距离，选择距离最近且小于设定阈值的点对作为对应圆点中心，这样就获得了圆点中心点与标定模板坐标之间的一一对应关系。

算法流程如图3所示。

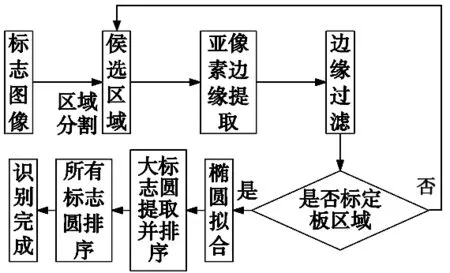
图3 算法流程图

2.2 标定板候选区域提取

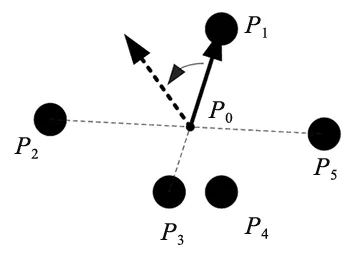
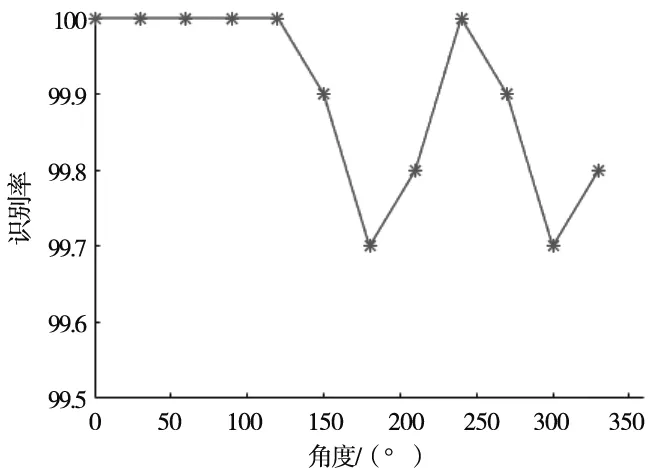
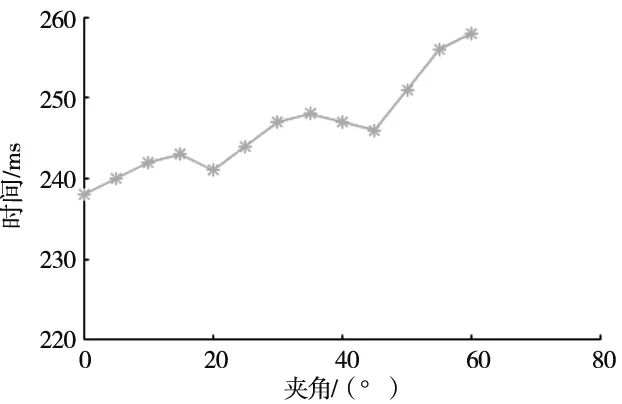
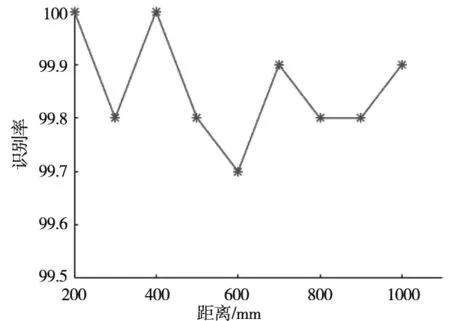
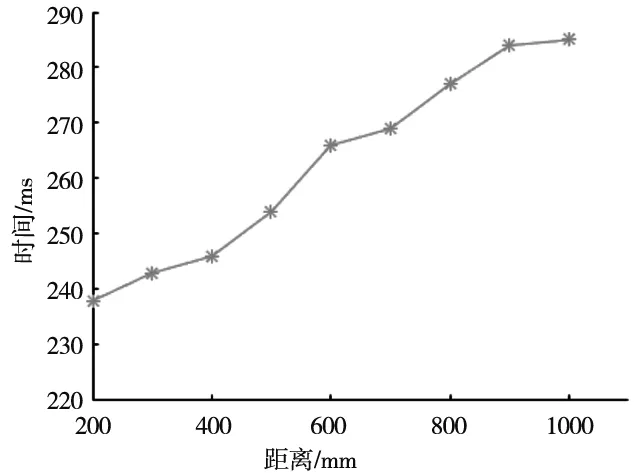
为增强图形对比度和方便识别，标定板通常为白底黑圆或者黑底白圆，此时可以采用阈值分割的方法可以对标定板区域进行初步的分割。若标定板在图像中的颜色阈值范围为[c1,c2](c1

(1)

此外，标定板在图像中的面积比例为大于0小于等于1的数值，通过计算候选区域的面积在整幅图像中的比例，这样就可以得到标定板的候选区域。

2.3 标志圆的识别

对所有标定板候选区域进行标志圆识别，包含标志圆的亚像素边缘提取、边缘过滤和圆心坐标排序。

2.3.1 标志圆亚像素边缘提取

对候选的标定板区域分别进行边缘提取，如使用Canny、Sobel等算子。但是此时得到的是像素级别边缘，为提高识别精度，通常使用亚像素边缘提取算法。基于伪Zernike矩的亚像素边缘检测算法具有矩的旋转不变性，在相同阶数的情况下，伪Zernike矩比传统Zernike矩包含目标物体更多的特征向量，且对噪声不敏感。对于数字图像，伪Zernike矩的离散形式可以表示为：

(2)

(3)

(4)

Vnm(ρ,θ)=Rnm(ρ)eimθ

(5)

首先建立理想的边缘检测模型:

(6)

其中，h和h+k分别是直线左右两侧的灰度值，θ是边缘与x方向的夹角，ρ是边缘中心到直线的距离，也是边缘所在的位置。

真实的亚像素边缘的求解公式为:

(7)

其中，x,y是单位圆中心坐标，详细计算过程参考文献[14-15]。

2.3.2 标志圆边缘过滤规则

由于提取到的边缘包含噪声信息，所以首先对其进行过滤，以去除非圆点的边缘。通常遵循以下过滤原则：

(1)边缘闭合原则

计算每个边缘的首像素和末尾像素之间的距离l，若l> 0，则舍弃该边缘。

(2)区域灰度值判定

计算闭合边缘区域内所有像素的平均灰度值，设最小阈值为m1，最大阈值为m2，均值m应满足m1

(3)区域面积判定

计算圆点闭合区域所包围区域的面积s，s应满足：

smin

(8)

(4)椭圆度判定

经过上述原则的过滤，能滤除大部分非标志点的边缘信息。而后可以根据提取到的符合条件的边缘的个数是否大于等于标定板圆点个数来判定候选区域是否是标定板所在位置。

2.4 标志圆排序

标志点排序的目的是为了获得所有圆点中心图像坐标与标定板三维坐标之间的对应关系。需要首先使用5个大圆获取图像坐标与三维坐标之间的射影变换矩阵，然后根据变换矩阵对所有的圆点进行排序。

2.4.1 大圆排序

在对提取到的边缘进行过滤后，进行椭圆拟合，计算椭圆的长轴半径。根据长轴半径的大小对椭圆按照从大到小的顺序进行排序，取前5个数值作为5个大圆的圆心。然后使用下述方法对5个大圆进行排序：

(1)计算5个大圆圆心之间的图像距离并进行排序，圆心距离最远的两个圆记为P2，P5(或者P5，P2此时顺序不确定)，同样的距离最近的两个圆记为P3，P4(或者P4，P3)，则剩下的一个圆记为P1；

(2)计算5个圆心的几何中心P0；

(3)连接点P0和点P1，以向量P0P1为起始边，逆时针旋转并计算剩余4个圆心与该线段之间的距离，当距离为零时，该圆点通过该直线，据此可以顺序获得P2、P3、P5、P4；这样就唯一确定了5个大圆点的顺序，如图4所示。

图4 排序方法示意图

2.4.2 射影变换矩阵的计算

平面射影变换是关于齐次三维坐标的线性变换，可以使用一个非奇异3×3矩阵H表示，若图像坐标用[x,y,1]t表示，对应的三维坐标用[X,Y,1]t表示，那么两者之间的转换关系为：

(9)

此矩阵H乘以任意一个非零比例因子不会使射影变换改变，也就是H是一个齐次矩阵，在9个元素中有8个独立比率，故一个射影变换具有8个自由度，因此求解H矩阵的值需要至少4个点。将上面计算得到的5个大圆的圆心和对应的标定板坐标代入上式，即可计算得到H矩阵[13,16]。

2.4.3 所有圆点的排序

将标定板圆心坐标通过H矩阵映射到图像坐标系中，理论上，该映射的坐标值与实际检测的坐标值应该重合，但是由于存在计算以及成像误差，两者之间存在一定的差值。若投影点的坐标为P(x,y)，实际成像点的坐标为P(x′,y′)，那么两点之间的距离为：

(10)

计算投影点坐标与所有实际像点之间的距离值，设最大阈值为dmin，那么取距离最小且dist

3 实验

实验使用如图5所示的黑色背景白色标志点的标定板，包含11×9个圆点图案，其中包含5个大圆，大圆半径为4 mm，小圆半径为2 mm，圆心之间的距离均为10 mm，标称精度为0.001 mm。所用标定相机型号为大恒相机MER-200-20GM黑白相机，分辨率为1292×964，配备computar生产的8 mm镜头。标定实验程序使用C++编写，运行在64位版本windows7上，计算机主要配置为Intel i5-3470 CPU，运行内存为8G。

图5 实验器材

使用上述相机拍摄标定板在不同角度和距离下的图像，然后标定板图像进行识别。如图6所示为标定板识别效果图，99个标志点每次均按照固定的顺序进行排列。重点实验了在同一距离不同角度、同一角度不同距离下标定板的识别效果和时间。

图6 标定板识别效果图

(1)将标定板放置在约300 mm的位置上，首先实验标定板水平放置，此时标定板平面与像平面大致平行，夹角约为0°。将标定板在水平面内以间隔约30°角转动，运行识别程序，验证识别速度和效果，如图7所示为各角度下的识别效果。

图7 同一平面内不同角度识别结果(部分)

分析了在不同曝光值下的识别率以及识别速度，如图8所示，在合理的曝光值下，在各角度下均可以取得接近100%的识别率，说明平面内的旋转角度对识别效果没有影响；如图9所示，在同一距离不同角度对识别速度的影响不大，单幅图像识别时间在240 ms左右。

图8 不同角度下的识别率

图9 不同角度下的识别时间

(2)保持标定板与相机的距离、曝光值不变，改变标定板与相机像平面之间的夹角，以大约10°的间隔从0°旋转到60°。如图11所示，当夹角超过45°时，识别率明显下降，此时由于远离相机的标志点可能超出变形较大，边缘模糊，因此通常无法拟合得到正确的椭圆；如图12所示，角度变化对识别时间的影响不大。

图10 不同夹角下的识别结果(部分)

图11 不同夹角下的识别率

图12 不同夹角下的识别时间

(3)保持像平面与标定板之间的夹角不变，改变两者之间的距离，从200 mm到1000 mm以100 mm的间隔递增，在每个位置对相机进行对焦，使得在该距离上能获得清晰的图像。在不同距离上的识别效果(部分)如图13所示，识别率如图14所示，距离对识别率影响不大，均能获得接近100%的识别率；识别时间如图15所示，随着距离的增大，识别时间有所增加，与候选区域增多有关，但是时间总体控制在300 ms以内。