改进遗传算法优化的矿井局部通风机模糊PID控制器设计
2021-09-28胡业林邓想郑晓亮
胡业林, 邓想, 郑晓亮
(安徽理工大学 电气与信息工程学院, 安徽 淮南 232001)
0 引言
煤矿用局部通风机是煤矿井下通风必不可少的安全设备,为了保证井下作业人员需氧量和瓦斯浓度不超限,局部通风机功率一般偏大且始终处于恒速运行状态,造成大量电能浪费[1]。随着变频技术的发展,局部通风机变频调速系统应运而生[2]。局部通风机变频调速系统需要根据瓦斯涌出量和工作面人员数量等因素确定供风量,而瓦斯涌出量具有随机性,使得局部通风机变频调速系统具有非线性、时变性、多干扰的特点。传统局部通风机变频调速系统多采用固定参数的PID控制器,无法满足时变通风机调速系统的控制要求,因此,多种智能算法被用于优化PID控制器。文献[3]针对PID控制参数调整困难的问题,提出了一种粒子群优化PID控制算法,相比于传统PID控制器,经过粒子群算法优化后的控制器对局部通风机转速控制输出性能改善明显。文献[4]针对矿井通风机控制系统的时变性,设计了模糊PID自适应控制系统,利用模糊算法对PID参数进行实时调整,实现了通风机转速的自适应控制。文献[5]针对模糊PID控制器中模糊规则的设定需要依赖人工经验的问题,提出利用遗传算法对模糊规则进行优化,提高了模糊PID控制器的控制效果。文献[6]针对传统模糊PID控制的许多参数需要结合实际情况进行调整、人为试错确定的问题,提出采用遗传算法对控制器的量化因子和比例因子进行优化,提高了控制器的精度和速度。文献[7]分析了隶属度函数与比例因子和量化因子的关系,并针对模糊PID控制存在人为确定隶属度函数的问题,提出采用改进遗传算法对隶属度函数进行优化,结果表明优化后的控制器性能更优。但是上述控制器的隶属度函数和模糊规则未能同时优化,剩余参数仍需根据经验选取,很难实现隶属度函数和模糊规则的最优组合。针对该问题,本文设计了一种改进遗传算法优化的矿井局部通风机模糊PID控制器(以下简称改进模糊PID控制器),该控制器在模糊PID控制器的基础上,利用改进遗传算法同时优化隶属度函数和模糊规则,从而实现局部通风机的最优风量控制。
1 改进模糊PID控制器设计
改进模糊PID控制器包括运算模块、模糊PID控制器和基于改进遗传算法的控制器优化部分,其结构如图1所示。利用改进的遗传算法同时优化模糊控制器的隶属度函数和模糊规则,可有效避免模糊PID控制器参数设置的主观性。利用传感器实时采集的数据计算需风量的设定值r,实现r的自适应调整。将r和当前实际风量值q进行比较,计算得到两者之间的偏差e和偏差变化率ec,将e和ec传送至优化后的模糊PID控制器,控制器输出控制电压u,用以控制矿用隔爆变频器,变频器调节异步电动机转速并经过风速转换,最终实现风量的自适应调节。
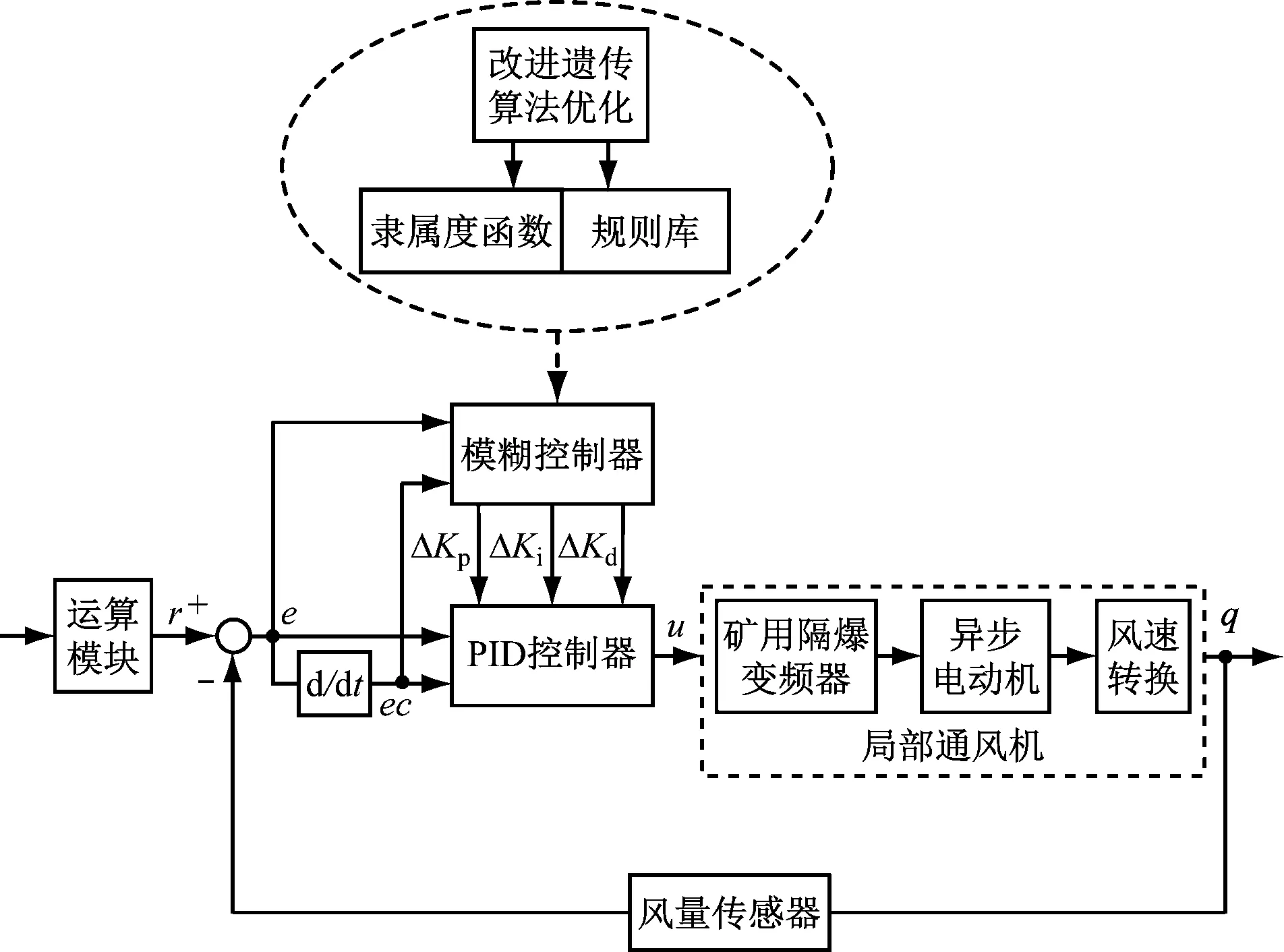
图1 改进模糊PID控制器结构Fig.1 Structure of improved fuzzy PID controller
1.1 运算模块
运算环节由可编程逻辑控制器PLC内部的运算模块实现,运算模块根据传感器采集到的工作面瓦斯涌出量w得到按瓦斯涌出量计算的需风量qw,qw和w成正比例关系。根据工作面人数g得到按工作面人数计算的需风量qg。比较qw和qg的大小,取两者的较大值作为运算模块的输出。
qw=wκ/ν
(1)
式中:κ为瓦斯涌出不均衡系数;ν为回风流中瓦斯的允许浓度。
qg=qming
(2)
式中qmin为每个工作面人员的最小供风量。
通过输出qw和qg中的较大值作为需风量的设定值,运算模块能够在保证工作面人员最小供风量的前提下,根据瓦斯涌出量自适应地调整需风量的设定值。利用优化后的模糊PID控制器良好的跟随性能控制局部通风机,使实际风量跟随需风量设定值的变化而变化,最终实现依据工作面瓦斯涌出量和人员数量自适应调整工作面风量的目的。
1.2 模糊PID控制器
模糊PID控制器包含1个模糊控制器和1个PID控制器。模糊控制器采用两输入、三输出的Mamdani控制器,将实际值和目标值之间的偏差e和偏差变化率ec作为模糊控制器的输入,PID参数的变化值ΔKp,ΔKi,ΔKd作为模糊控制器的输出。将Kp,Ki,Kd参数输入PID控制器,控制信号为u。在运行中通过不断检测e和ec,利用模糊控制器对PID控制器的3个参数进行实时修改,以满足不同的e和ec对控制参数的要求。模糊PID控制器具有良好的鲁棒性和动静态性能,但在传统情况下,控制器的参数均由人为主观设定,极大限制了控制器的控制性能。
(3)
式中Kp0,Ki0,Kd0为PID的初始参数。
(4)
1.3 基于改进遗传算法的控制器优化
在遗传算法中,种群表示所有可能解的集合,种群中包含许多个体,每个个体表示一种可能解,个体中又包含多个基因,基因表示这个可能解的具体信息。将遗传算法应用到模糊PID控制器参数优化中,首先需要根据隶属度函数和模糊规则的特点,利用特殊的编码方式,将二者的具体信息编码成个体中的基因;然后利用改进遗传操作对个体进行迭代寻优,迭代结束后输出种群中适应度最高的个体;最后将该个体的基因通过解码即可得到隶属度函数和模糊规则的最优组合。改进遗传算法优化隶属度函数和模糊规则的流程如图2所示。
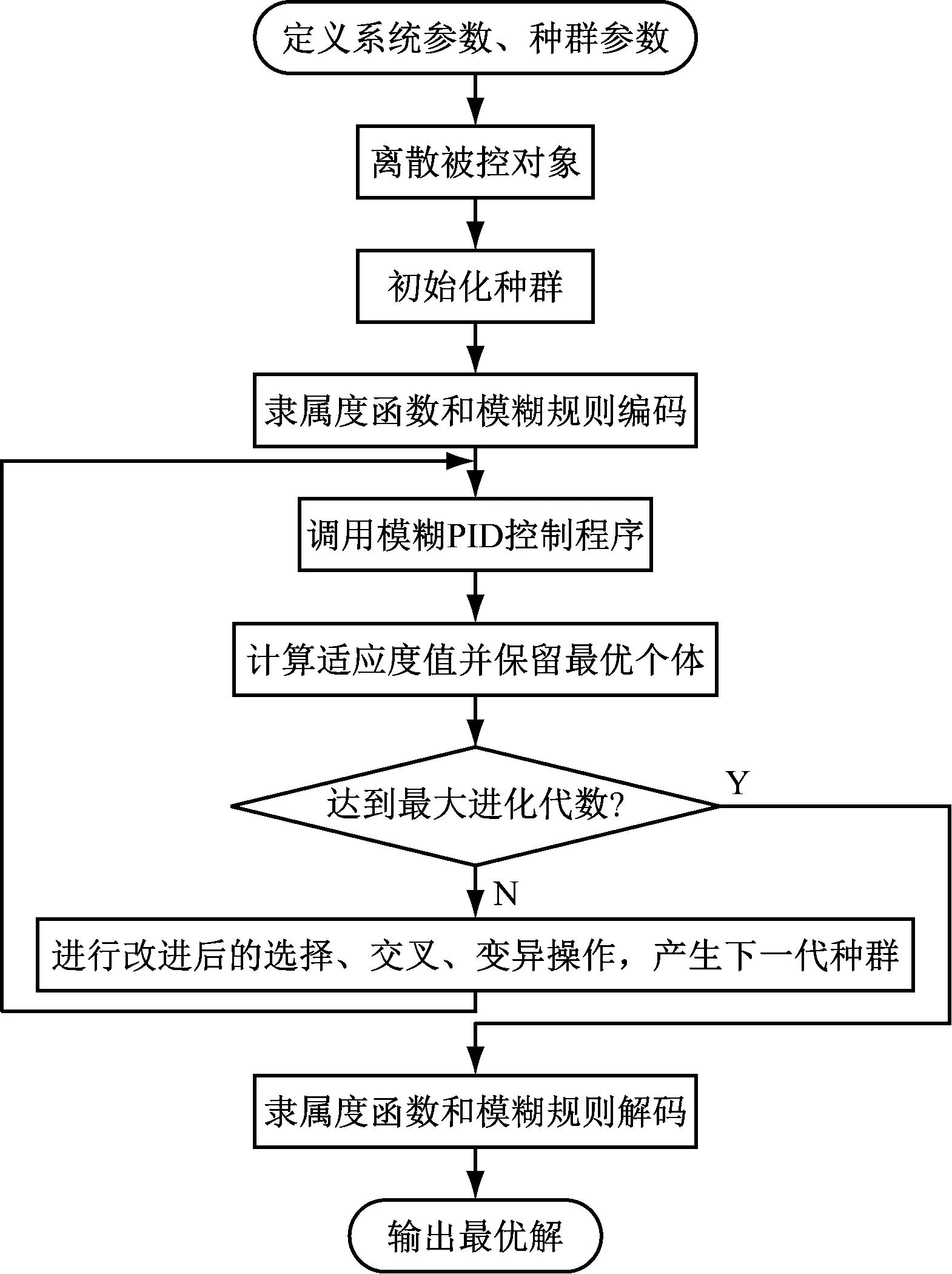
图2 改进遗传算法优化模糊PID控制器流程Fig.2 Flow of fuzzy PID controller optimized by improved genetic algorithm
1.3.1 初始化种群
在进行遗传操作前,需要先设置初始种群。为了实现全局搜索,本文选用随机方式产生初始种群。为了便于后续的编码操作,种群中的基因变化范围设置为[1,5]。
1.3.2 隶属度函数和模糊规则的编码与解码
常用的编码方式有二进制编码和实数编码,其中实数编码过程简单且不易陷入局部极值[8]。因此,本文选用实数编码形式对模糊规则和隶属度函数进行编码。对模糊规则进行编码时,设模糊子集为{负大,负小,零,正小,正大},即{NB,NS,Z,PS,PB},使用{1 2 3 4 5}表示。对隶属度函数进行编码时,基本论域设置为[-1,1]。模糊子集NS、Z、PS选用三角形隶属度函数,NB选用Z形隶属度函数,PB选用S形隶属度函数。为了便于编码,设隶属度函数的顶点和两侧隶属度函数交点的横坐标一致[9]。因此,只需确定隶属度函数的顶点坐标就可以确定整个隶属度函数的形状。由于隶属度函数的顶点坐标要求在一定范围内且顺序排列,若直接对其进行编码,经过遗传操作后可能无法满足上述要求,会出现许多无效编码。本文采用的方法是对隶属度函数顶点的横坐标在基本论域上的比例分数进行编码,比例分数无需满足范围内顺序排列的要求,可以与模糊规则的编码一起进行遗传操作。
由于4个基因可以确定1个变量的隶属度函数,模糊控制器一共有5个变量,即需要20个基因可以确定全部的隶属度函数。而每个模糊控制器的输出需要25条模糊规则,一共有3个输出,即需要75个基因可以确定全部的模糊规则。因此,每个个体应包含95个基因。个体的编码示例如图3所示,前20位基因表示隶属度函数编码,后75位基因表示模糊规则编码。

图3 个体编码示例Fig.3 Example of individual coding
经过遗传操作,最优个体后75位基因利用对应关系即可解码成相应的模糊规则,而前20个基因需要将比例分数转换成隶属度函数顶点的位置坐标后才能解码出相应的隶属度函数。
(5)
式中:α,β为正半轴的隶属度函数顶点的横坐标值;xα,xβ为α,β对应的比例分数。
以误差e的隶属度函数为例具体说明转换过程,误差e的隶属度函数如图4所示,a,b,c,d为隶属度函数的4个顶点横坐标值,且0≤a≤b≤1,-1≤d≤c≤0。x1,x2,x3,x4为误差e的隶属度函数的比例分数。将x1,x2代入式(5)得到隶属度函数的顶点横坐标值a,b,将x3,x4代入式(5)计算得到的结果添加负号,即可得到隶属度函数的顶点横坐标值c,d,得到4个顶点横坐标值后,即可解码出误差e的隶属度函数。

图4 误差e的隶属度函数Fig.4 Membership function of error e
1.3.3 适应度函数选择
个体适应度是遗传操作的基础,直接影响到算法的效果。本文采用设定值和实际值的误差e(t)的绝对值的积分作为目标函数。

(6)
由于误差绝对值的积分值越小表示适应度越好,所以,适应度函数描述为
(7)
为减少浮点数运算,将适应度值放大1 000倍。
1.3.4 改进的遗传操作
为了提高种群的适应度和多样性,对选择操作进行改进,引入欧氏距离[10]:
(8)
式中:ηi为个体η的第i个基因;θi为个体θ的第i个基因;n为基因个数。
欧氏距离越大表示个体η和个体θ的相似度越小。选择操作步骤如下:
(1) 计算种群中每个个体的适应度值和种群平均适应度值,记录最高适应度值及其个体。
(2) 逐个判断种群中个体的适应度值是否小于平均适应度值,若是,转到步骤(3),否则保存个体,直至判断完整个种群。
(3) 随机产生m个个体,分别计算这m个个体的适应度值与原种群中最高适应度值个体之间的欧氏距离,选择适应度值与欧氏距离之和最大的个体作为新的个体,取代种群中原有的个体。
交叉操作采用自适应交叉概率,根据当代种群中的平均适应度值Favr和最大适应度值Fmax对交叉概率p1进行自适应调整[11]。
(9)
式中:k1为交叉概率设定值;Fj为个体j的适应度值。
确定交叉概率p1后,按照交叉概率在种群中选择个体进行交叉运算。由于本文使用的是实数编码,所以使用算术交叉算子进行交叉运算[12]。
(10)
式中:Cη,Cθ为从种群中选择的2个父代个体;Cη+1,Cθ+1为经过交叉操作后产生的新的子代个体;ε为(0,1)内随机产生的系数。
变异操作采用自适应的变异概率p2,其形式和式(9)一致。同时由于是利用实数编码,采用算术变异算子进行变异运算。如对个体的第i个基因进行变异[13],其公式如下:
(11)
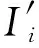
2 仿真分析
2.1 局部通风机控制模型建立
在进行仿真分析之前,需要先建立局部通风机的控制模型。在局部通风机控制系统中,通过控制变频器输入电压实现电动机转速调节,再经过电动机转速和风速的转换,最终实现局部通风机风速的调节。因此,可以使用变频器和异步电动机来近似等效局部通风机的结构。
变频器输入电压和输出频率之间的数学模型可以近似等效为一阶惯性环节,其传递函数为[14]
(12)
式中:KUF为变频器的输出频率和输入电压的比值;TUF为变频器时间常数,一般取变频器加速时间的60%;s代表复频域。
异步电动机输入频率和输出转速之间的数学模型可以近似等效为一阶惯性环节,其传递函数为[14]
(13)
式中:KMA为异步电动机额定转速与工频的比值;TMA为异步电动机时间常数,一般取电动机启动时间的25%。
以FBD-No7.1型矿用隔爆型对旋轴流局部通风机为研究对象,通风机参数见表1。取变频器最大输入电压为5 V,输出频率为20~50 Hz,加速时间为0.3 s。异步电动机启动时间为2.4 s。由式(12)、式(13)可得到变频器数学模型和异步电动机数学模型分别为
(14)
(15)

表1 FBD-No7.1局部通风机参数Table 1 Parameters of FBD-No7.1 local ventilator
由式(14)、式(15)得到局部通风机转速控制数学模型为
(16)
建立局部通风机转速控制的数学模型后,要实现局部通风机风量的调节,还需要进行转速和风量的转换。根据通风机的特性可知,转速和风量之间满足正比例关系[15]。依据局部通风机参数,通风机的转速和风量转换关系式为
(17)
式中:q为通风机风量;qe为通风机额定风量;ze为通风机额定转速;zv为通风机转速。
2.2 仿真分析
为验证改进模糊PID控制器的控制性能,选用矿井局部通风机的数学模型作为控制对象,分别采用PID、模糊PID和改进遗传算法优化后的模糊PID三种控制方式,对比三者的单位阶跃响应曲线,分析3种控制器的控制性能。
设遗传代数为100,种群大小为20,交叉概率系数kc为1,变异概率系数km为0.5,传递函数的采样时间为0.1 s。遗传进化过程目标函数J的变化曲线如图5所示。从图5可看出,标准遗传算法SGA(Standard Genetic Algorithm)在67代达到收敛。而由于提高了种群的多样性和算法的收敛性,改进遗传算法IGA(Improved Genetic Algorithm)在第10代就达到收敛且收敛数值要小于SGA的收敛数值,IGA收敛速度更快并且寻优结果更好。

图5 目标函数J的变化曲线Fig.5 Change curves of objective function J
经过IGA优化后,获得最优个体为{3443,2423,4322,4232,2233,54322,53223,43432,23323,21213,43432,54334,14332,41323,22322,41333,22454,34433,34333,22333}。经过解码可以得到优化后的模糊控制器模糊规则库(表2)和隶属度函数(图6)。

表2 改进遗传算法优化后的ΔKp/ΔKi/ΔKd的模糊规则库Table 2 Fuzzy rule base of ΔKp/ΔKi/ΔKdoptimized by improved genetic algorithm

将得到的隶属度函数和模糊规则库代入到模糊PID控制器中。利用Z-N法整定PID控制器的参数,Kp=0.16,Ki=0.2,Kd=0.022。设模糊PID控制器和改进模糊PID控制器的初始参数Kp0=0.2,Ki0=0.25,Kd0=0.03。同时为对比抗干扰能力,在0.2 s处加入幅值为0.2的扰动信号。3种控制器的单位阶跃响应曲线如图7所示,输出结果比较见表3。

图7 3种控制器的单位阶跃响应曲线Fig.7 Unit step response curves of three kinds of controller
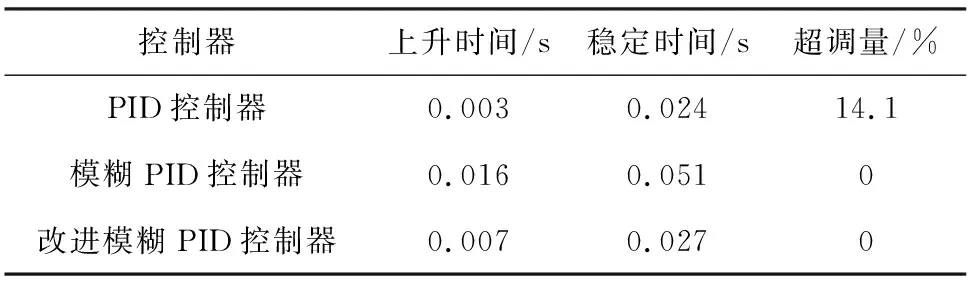
表3 3种控制器的输出结果比较Table 3 Comparison of output results of three kinds of controller
由图7可看出,在0.2 s加入幅值为0.2的干扰信号后,PID控制器在0.219 s恢复稳定,最大扰动幅值为1.064;模糊PID控制器在0.229 s恢复稳定,最大扰动幅值为1.023;改进模糊PID控制器在0.216 s恢复稳定,最大扰动幅值为1.032。改进模糊PID控制器受到干扰后,最大扰动幅值适中且恢复时间最短。说明改进模糊PID控制器的控制效果最佳,抗干扰能力最强。
由表3可看出,PID控制器由于参数固定不变,虽然可以实现较短的上升和稳定时间,但却有明显的超调。模糊PID控制器能够根据不同的控制要求自适应调整控制器的参数,基本没有超调量,但由于控制器的隶属度函数和模糊规则是根据经验设置的,具有较大的主观性,限制了模糊PID控制器的控制效果,使得模糊PID控制器的上升和稳定时间较长。改进模糊PID控制器利用改进遗传算法的寻优能力,实现了控制器中隶属度函数和模糊规则最优组合,使得其在没有超调的情况下,较模糊PID控制器上升时间缩短了56.25%,稳定时间缩短了47.06%。
3 结论
(1) 由于矿井局部通风机具有时变、非线性的特点,固定参数的PID控制器很难达到良好的控制效果。为了更好满足矿井局部通风机的控制要求,设计了一种基于改进遗传算法优化的模糊PID控制器。同时对于传统遗传算法容易出现局部最优解和早熟的问题,在改进遗传算法中引入欧氏距离来提高算法中种群的多样性,同时引入自适应交叉和变异概率来提高算法的收敛性。在编码过程中采用比例分数间接实现对隶属度函数的优化,使得改进遗传算法能够同时优化隶属度函数和模糊规则。将优化得到的隶属度函数和模糊规则导入模糊PID控制器中,通过不断检测误差e和误差变化率ec,根据模糊规则实时调整PID的3个参数,实现控制器对矿井局部通风机的自适应控制。
(2) 以矿井局部通风机的数学模型作为控制对象,测试PID控制器、模糊PID控制器、改进模糊PID控制器的单位阶跃响应曲线。对比结果显示,PID控制器有较大的超调量,模糊PID控制器和改进模糊PID控制器基本没有超调,同时改进模糊PID控制器相较模糊PID控制器上升时间缩短了56.25%,稳定时间缩短了47.06%。在受到信号干扰后,改进模糊PID控制器最大扰动幅值适中且恢复时间最短。改进模糊PID控制器能够更好地满足矿井局部通风机的控制要求,对矿井局部通风机的变频控制系统优化具有一定意义。
