部分频带干扰下的OFDM 系统干扰检测与分集抑制算法

李果，文妮，宫丰奎，张剑，张思瀚

（1.西安电子科技大学ISN 国家重点实验室，陕西 西安 710071；2.中国西南电子技术研究所，四川 成都 610036）

1 引言

正交频分复用（OFDM,orthogonal frequency division multiplexing）作为一种多载波调制方式，具有高频谱利用率、抗频率选择性衰落和易调制解调等优点，已被广泛应用于多个无线通信场景和多个无线通信标准中[1]，例如最新的长期演进技术升级版（LTE-A,long term evolution-advanced）[2]、第五代新空口（5GNR,5th generation new radio）移动通信技术[3]、第二代地面数字电视广播（DVB-T2,the second generation of digital video broadcasting-terrestrial）[4]、无线局域网（WLAN,wireless local area network）标 准 IEEE 802.11a/g/n/ac[5]等。然而，OFDM 系统对通信过程中的干扰非常敏感，即使是少量的带内干扰也会因频谱泄漏给OFDM 系统带来显著的性能损失[6]。随着无线通信系统的多样性发展，信道环境愈发复杂恶劣，影响OFDM 系统性能的干扰类型也越来越多，具体可分为两类：一类是无意干扰，主要包括自然气候干扰、人类活动干扰以及信道间干扰，例如蓝牙等短距离无线通信设备在通带内会影响WLAN（IEEE 802.11g/n）[7]，业余无线电产生的射频干扰会影响数字用户线路（DSL,digital subscriber line）系统[8]和电力线通信（PLC,power line communication）系统[9]，作为5G 关键技术之一的物联网（IoT,Internet of things）也不可避免地会将干扰引入OFDM 系统中[10]；另一类则是蓄意的人为干扰，较常出现在电子对抗中，其目的是尽可能地对敌方通信进行有效的干扰，从而达到降低敌方通信系统性能或者使其完全瘫痪的目的[11]，典型的人为干扰有单音干扰、多音干扰以及部分频带干扰。因此，保证干扰环境下OFDM 信号传输的可靠性至关重要。近年来，很多专家学者研究了OFDM 系统接收端抗干扰关键算法，主要包括干扰检测算法[12-18]和干扰抑制算法[19-25]。

常见的干扰检测算法主要针对窄带干扰和宽带干扰场景，其中，窄带干扰检测理论技术发展成熟，而宽带干扰检测相对窄带干扰检测存在明显的难点及差异，其一是在相同干扰功率下，宽带干扰降低了信干比，从而要求干扰检测算法具有更灵敏的检测性能；其二是宽带干扰导致无法恢复的干扰数据量加大，从而使整体解调性能急剧下降，因此需要干扰检测算法能够检测出更加准确的干扰边界，以提高后续干扰抑制算法性能。

根据干扰抑制实施的阶段不同，国内外现有的干扰抑制技术一般可分为时域法和频域法。时域法主要通过加窗减轻频谱泄漏的影响或者采用陷波滤波器滤除干扰；频域法主要通过对干扰位置处的信号置零或进行比例缩放，或者对干扰进行重构，以达到干扰抑制的效果。相比于时域法，频域法由于算法实现复杂度低、干扰抑制效果好等优点获得了广泛的应用。

从实际的通信干扰和抗干扰系统来看，常见的电子压制性干扰可分为瞄准式干扰、阻塞式干扰和扫频式干扰，本文考虑的集中式部分频带干扰属于阻塞式干扰。由于阻塞式干扰作用的是一段连续的频段，如不采取有效干扰避免或干扰抑制策略，接收性能将会严重恶化，且恶化程度随着干扰带宽比例的增加而加剧。目前实际系统中对抗该种干扰的方式主要是在更大的带宽范围内进行频率捷变，并且变化的范围越宽，对抗效果越好。本文所提算法的初衷是在不占用更宽频带的条件下，尽可能达到抑制或减缓阻塞式干扰的目的。本文主要针对宽带干扰中的集中式部分频带干扰场景，研究其频域干扰检测算法和频域干扰抑制算法。

1.1 干扰检测算法研究现状

目前，针对OFDM 系统的频域干扰检测算法主要有均值检测法[12]、连续均值去除（CME,consecutive mean excision）算法[13]、前向连续均值去除（FCME,forward consecutive mean excision）算法[14]以及一些基于FCME 的拓展算法，例如基于双阈值的定位算法（LAD,localization algorithm based on double-thresholding）[15]、归一化双阈值算法（LAD NT,LAD with normalized threshold）[16]、相邻簇合并双阈值算法（LAD ACC,LAD with adjacent cluster combining）[17]、三阈值FCME 算法[18]等。其中，均值检测法是利用提前设置的门限因子与接收信号功率谱线均值的乘积作为最终的检测门限，该门限计算复杂度低，但其固定单一，无法自适应信道环境中动态干扰的变化，缺乏通用性；CME 算法起初认为原始接收信号中是不存在干扰的，通过不断地比较接收信号幅值与更新的门限检测值以去除有用信号中的干扰，CME 算法中门限检测值的迭代过程可以适应信道中干扰功率的变化，解决了均值检测算法中门限检测值无法自适应干扰环境的问题，但当干扰信号功率较小时，容易出现漏检干扰的情况；FCME 算法假定一些幅值较低的信号是没有受到干扰的，先计算得到一个较小的干扰检测门限，从而避免了当干扰信号较小时出现遗漏干扰的情况，但由于FCME 算法包含排序过程，算法复杂度高于CME 算法。

以上介绍的几种算法阈值单一，当设置阈值太小时，易出现错误检测的情况；当设置阈值太大时，易出现漏检干扰的情况，因此LAD 算法基于上下2 个不同的阈值进行干扰检测，下阈值用于将相邻的干扰信号样本组成簇，而上阈值用于判定簇中的信号是否为干扰信号，这样可以避免单一阈值算法易出现的漏检及误检问题，从而进行准确的干扰定位。为了获得2 个检测门限，LAD 算法需要利用高低门限因子基于FCME 算法运行2 次，计算复杂度高；LAD NT 算法在LAD 算法基础上进行改进，该算法仅使用一个阈值，再利用2 个固定系数得到2 个检测门限，只需要基于FCME 算法运行一次，从而在不损失LAD 算法性能的前提条件下有效降低计算复杂度，但是偶尔会出现由于噪声的影响使部分干扰信号分量低于下阈值，导致干扰信号检测不完整的问题；因此，LAD ACC 算法在LAD NT 算法的基础上使用了一个额外条件，即如果检测到的干扰簇被低于下阈值的n个或更少的样本分开，则确定这些干扰簇是由一个干扰信号引起的，然后将这些干扰簇和阈值以下的样本连接在一起，解决了LAD NT 算法出现的干扰信号分离的问题，从而提高了LAD NT 算法的干扰检测性能。

上述双门限算法在某些通信场景中都存在一个问题，即当接收信号的信噪比很大时，主信号幅值远在噪声水平之上，双门限检测算法无法正确判别有用信号和干扰信号。因此，文献[18]提出了三阈值FCME 算法，该算法在LAD 算法的上下阈值之间加入了一个中阈值。当信号功率较弱时，中阈值可实现原来上阈值判定干扰的功能；当信号功率较强时，中阈值可实现原来下阈值的功能，以达到尽量保留有用信号的目的，从而解决了双门限算法存在的问题，提高了正确识别干扰的概率，但该算法仅适用于接收信号信噪比动态范围大的扩频通信场景。综上，目前的频域干扰检测算法大多是基于FCME 算法进行的改进，FCME 算法的干扰检测性能从根本上影响着改进算法的干扰检测性能。

1.2 干扰抑制算法研究现状

在OFDM 系统中，典型的频域干扰抑制算法是频域置零算法[19]，它通过对幅值大于设定阈值的干扰子载波采用置零处理来抑制大部分干扰能量。但由于干扰存在频谱泄漏，置零算法在抑制干扰的同时会丢失许多有用的信号，导致解调失败，因此其干扰抑制性能较差。从减少干扰频谱泄漏这个角度出发，文献[20]提出了一个连续干扰抑制算法，该算法基于硬判决对子载波依次进行干扰估计，然后线性预测前k个子载波干扰估计结果对第k+1 个子载波的干扰贡献，并将干扰估计结果进行反馈迭代以提高干扰估计准确度，降低干扰频谱泄漏，从而改善系统干扰抑制性能，但采用硬判决会损失较多有用信息，导致干扰抑制性能无法得到大幅提升。针对文献[20]的问题，文献[21]提出一个基于软判决的连续干扰抑制算法，与采用硬判决的方式比较，软判决尽最大可能地利用接收数据符号中的干扰信息，更有效地对干扰进行估计，从而更进一步地提升了系统干扰抑制性能，但同时也相应地增加了计算复杂度。

不同于以上介绍的算法，文献[22]转换另一种思路，提出了一种基于调制重叠双正交变换（MLBT,modulated lapped biorthogonal transform）的干扰抑制技术，与基于传统快速傅里叶变换（FFT,fast Fourier transformation）的干扰抑制技术相比，此变换域干扰抑制算法具有更好的误比特率性能，对干扰频率偏移具有更强的稳健性，但MLBT 比FFT计算复杂度要高得多。文献[23]为实现干扰抑制提供了另一个新思路，设计了一个最小化频谱泄漏的干扰抑制方案，主要思想是先在时域利用估计的干扰频率将干扰搬移到一个使频谱泄漏最小的频点位置，然后在频域对干扰进行消除，最后再变换到时域以去除信号中引入的干扰频率，由于利用了2 次时频域转换，其计算复杂度也相对较高。进一步地，文献[24-25]分别在加性白高斯噪声（AWGN,additive white gaussian noise）信道和多径衰落信道下理论分析了文献[23]算法中干扰数目、频率以及振幅对接收端信干噪比的影响，并仿真验证了理论分析的正确性，但该理论分析的前提条件是干扰频点之间间隔足够大，相互之间串扰程度极小，其分析结果适用范围较小。针对文献[24-25]存在的问题，文献[26]提出了一种联合时频域的多交互干扰抑制算法，该算法利用无限冲击响应（IIR,infinite impulse response）陷波滤波器和 CZT（chirp z-transform）抑制多个相互作用的干扰信号，从而提高了OFDM 系统在复杂干扰环境下的稳健性。文献[27]针对OFDM 系统中FFT 导致干扰频谱泄漏，从而降低系统性能的问题，提出了一种基于人工神经网络的干扰抑制技术，该技术首先采用FCME 算法对接收信号进行预处理，然后利用人工网络结构从时域提取特征值并进行干扰频率估计，以提高通信系统的性能。文献[28]提供了另一个新思路以实现干扰抑制，在稀疏贝叶斯学习框架下，提出了一种基于层次先验模型的分层变分贝叶斯算法，该算法可以联合估计数据符号及相位噪声，以解决干扰的稀疏估计问题，仿真结果表明该算法具有比传统算法更好的误比特率（BER,bit error ratio）性能。另外，针对小区间干扰，文献[29]提出了一种利用相邻小区间干扰来提高2 个小区接收信号质量的协议，并设计了最优的中继预编码器，以使中继总功率最小，仿真结果验证了最优中继预编码方案结合该传输协议在多小区间干扰抑制性能方面的优势，且可以大大降低功耗。

从上述描述的算法可以看出，现有的很多频域干扰抑制算法由于在接收端引入复杂的干扰抑制机制，都存在实现复杂度高的问题，且大多算法只对具有频域稀疏性的干扰展开研究，其适用范围有限。

1.3 本文贡献

本文对频域干扰检测算法和频域干扰抑制算法展开研究，主要贡献如下。

1) 为提高经典FCME 算法的干扰检测性能，提出了一种具有高检测概率的干扰检测算法，即基于前向连续方差去除（FCVE,forward consecutive variance excision）的干扰检测算法，理论推导了提出算法的门限因子表达式，设计了相对应的干扰检测门限值计算方法，并给出了该干扰检测算法的具体实现步骤。

2) 为解决传统频域干扰抑制方案实现复杂度高且适用范围有限的问题，提出了一种基于频率分集的干扰抑制算法，介绍了算法的主要思想，并给出了其具体实现过程。该算法既保证干扰抑制性能，具有低实现复杂度，又能够自适应一定的动态干扰场景。

2 模型建立

2.1 系统模型

多载波OFDM 系统干扰检测与抑制框架如图1所示。图1 中，发射机输入数据流依次经过编码、多载波星座调制、子载波映射、快速傅里叶逆变换（IFFT,inverse fast Fourier transformation）、插循环前缀（CP,cyclic prefix）生成OFDM 基带信号，然后经过上变频及数/模变换（DAC,digital-analog convert）处理将信号发送到存在部分频带干扰的信道中，到达接收机的信号，经过模/数变换（ADC,analog-digital convert）及下变频处理后获得基带信号，然后依次经过去CP、FFT、干扰检测、干扰抑制、信道估计与均衡、解调、译码处理，得到最终的输出数据流。

从图1 中可以看出，接收信号经过FFT 到频域后，开始进行干扰检测和干扰抑制处理，本文主要针对频域干扰检测技术和频域干扰抑制技术展开研究。

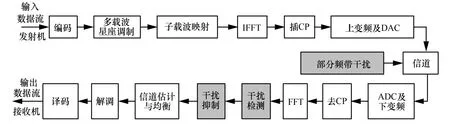
图1 多载波OFDM 系统干扰检测与抑制框架

2.2 部分频带干扰模型

当干扰信号功率集中占据有用信号频带宽度W内的某一段时，此时的干扰即为连续频段内的集中式部分频带干扰，在这里，将部分频带干扰建模为加性白高斯噪声[30]，其干扰带宽WJ相对工作频带的大小可由干扰因子r表征，r=WJ/W。

通常在仿真系统中，利用一个带限滤波器对宽带高斯白噪声信号进行滤波处理，即可得到部分频带干扰i(t)

其中，j(t)表示宽带噪声信号，带限滤波器h(t)在频域可表示为

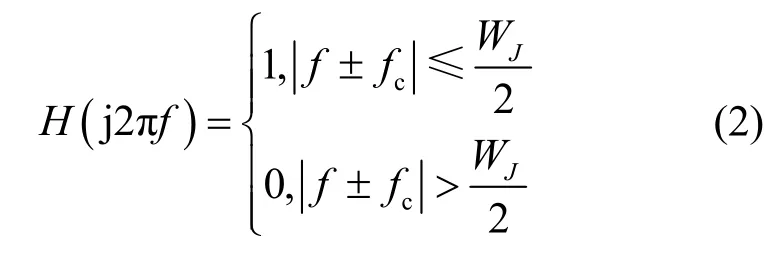
其中，fc表示带限滤波器的中心频率。

3 干扰检测与干扰抑制算法

3.1 基于FCVE 的干扰检测算法

本文提出的基于FCVE 的干扰检测算法的基本思想是当信道中存在干扰时，到达接收端的信号既包括有用信号也包括干扰信号，因干扰功率和信号功率存在一定差异，致使信号功率谱线的包络产生波动。相比于传统FCME 算法利用谱线均值来区分干扰信号和有用信号，采用谱线方差的形式更容易将其进行区分。因此FCVE 算法是通过利用信号谱线的方差来迭代更新干扰检测门限值。这里需要说明的是，以谱线均值为测度利用的是一阶统计量，以谱线方差为测度利用的是二阶统计量，二阶统计量能够有效增大干扰子载波上信号幅度方差与未干扰子载波上信号幅度方差的区分程度，因此采用谱线方差的形式具备更强的干扰检测分辨能力。下面推导FCVE 算法的门限因子，并介绍其具体实现步骤。

3.1.1 门限因子计算

门限因子表征了系统接收信号频域包络方差归一化的检测门限大小。当信道噪声功率远大于有用信号功率时，接收信号的频域包络Ψ统计意义上近似服从Rayleigh 分布[13]，其概率分布函数为

其中，σ2为噪声方差。由式(3)可得

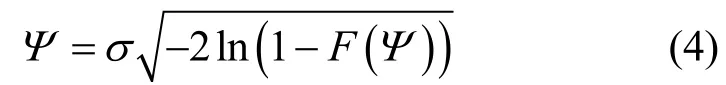
基于式(4)、Ψ的均值以及方差D(Ψ)=(4-π)σ2/2，理论推导出门限因子TFCVE的闭式表示形式为

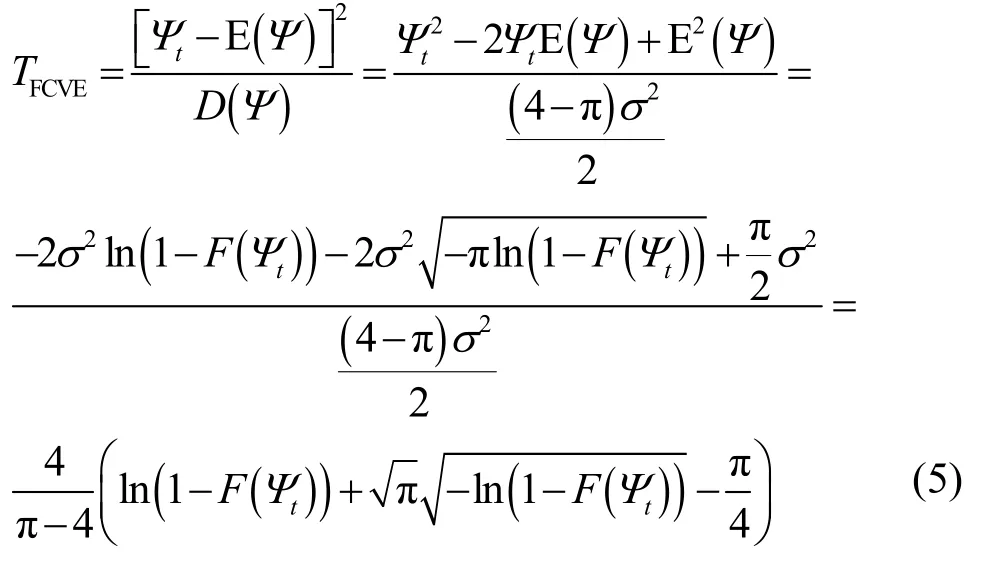
其中，Ψt为检测门限值，F(Ψt)为信号谱线幅度的统计概率，即F(Ψt)=0.99 表示接收信号频谱幅度大于检测门限的概率为1%。

相比而言，在文献[14]中，FCME 算法的门限因子TFCME可表示为

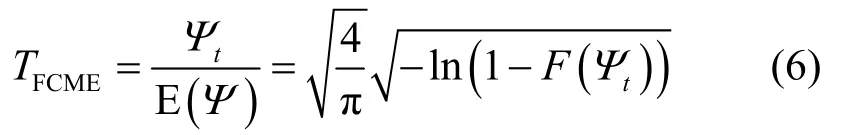
从式(5)和式(6)可以看出，FCME 算法是利用接收信号均值计算门限因子，而FCVE 算法是利用接收信号方差计算门限因子。表1 给出了FCME 算法与FCVE 算法在不同概率分布条件下的门限因子。

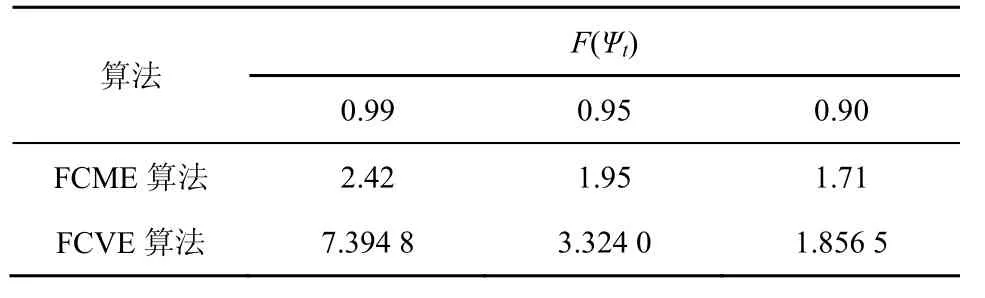
表1 FCME 算法与FCVE 算法在不同F(Ψt)下的门限因子

将FCVE 算法在不同F(Ψt)下的理论门限因子值与仿真门限因子值进行对比，结果如图2 所示。

图2 FCVE 算法在不同F(Ψt)下理论门限因子值与仿真门限因子值对比

对比表1 和图2 可得，当F(Ψt)=0.99、0.95、0.90 时，仿真门限因子值与理论门限因子值高度相似，说明了式(5)中门限因子TFCVE表达式推导的正确性。

3.1.2 算法具体实现步骤

设置接收信号频谱幅度集合Ψ={Ψ(1),Ψ(2),...,Ψ(k),...,Ψ(N)}，其中N为FFT 点数，有用信号频谱幅度集合为ΨS，干扰信号频谱幅度集合为ΨI，门限因子为TFCVE，迭代次数上限为K，FCVE 算法的具体实现步骤如下。

1) 初始化。升序排列集合Ψ中所有元素，选择较小的P个值作为集合ΨS的初始元素，假设这P个值没有受到干扰，然后将Ψ中的剩余元素放入ΨI中，n=1。

2) 设置干扰检测门限。计算ΨS={ΨS(1),ΨS(2),...,ΨS(i),...,ΨS(P)}的均值，方差，干扰检测门限通过TFCVED(ΨS)计算得到。

3) 更新ΨS、ΨI以及P。将ΨI={ΨI(1),ΨI(2),...,ΨI(i),...,ΨI(N-P)}中各元素按公式[ΨI(i)-E(ΨS)]2与门限TFCVED(ΨS)比较，若小于干扰检测门限，则将其从集合ΨI中剔除并添加到集合ΨS中，此时P为集合ΨS中的元素个数。

4) 得到最终的检测门限：n=n+1，跳转至步骤2)，重新计算E(ΨS)及D(ΨS)，更新干扰检测门限值，直到步骤3)中ΨI的所有元素按公式[ΨI(i)-E(ΨS)]2均大于检测门限值或达到最大迭代次数K为止，将完成最终迭代的信号幅度方差值记为D(ΨS)end，则最终的检测门限为TFCVED(ΨS)end。

5) 得到最终的干扰位置集合I={k|Ψ(k)＞TFCVED(ΨS)end}。

由上述步骤可以看出，将设定的门限因子与接收信号的方差相乘可得到FCVE 算法的干扰检测门限值，然后利用该门限值迭代更新干扰信号集合和有用信号集合，从4.1 节中的干扰检测性能评估仿真结果可以看出，相较于FCME 算法利用接收信号均值产生干扰检测门限值，FCVE 算法能以更高的概率检测出有用信号中的干扰信号。

3.2 基于频率分集的干扰抑制算法

本文提出的基于频率分集的干扰抑制算法的主要思想是将同一星座符号映射到2 个不同的有效子载波位置上，当某些有效子载波位置上的符号受干扰程度较大时，可以利用相对应的受干扰程度小的有效子载波位置上的符号进行补偿，以达到干扰抑制的目的。其具体实现方案为：在发送端，面向OFDM 系统子载波实现频率分集，生成具有抗干扰特性的OFDM 信号波形；在接收端，首先对频域接收信号进行干扰检测，然后采用选择合并方法估计得到频域发送信号。

本文提出的基于频率分集的干扰抑制算法的具体实现步骤如下。

1) 发送端基于频率分集生成抗干扰OFDM 信号波形

设OFDM 系统子载波个数为N，有效子载波个数为Nu，Nu≥2 且为偶数，其中第1～(N-Nu)/2 个和第(N-Nu)/2+Nu+1～N个子载波为空闲子载波，第(N-Nu)/2+1～(N-Nu)/2+Nu个子载波为有效子载波。首先将随机数据比特流进行星座调制，得到星座调制序列A={a1,a2,… ,au,…,aNu/2}，其中，au表示第u个星座符号，然后将星座调制序列A中的每个星座符号基于频率分集的思想进行载波映射，设频域发送信号X={x1,x2,…,xu,…,}，其中，xu表示第u个有效子载波符号，X中各元素通过式(7)得到

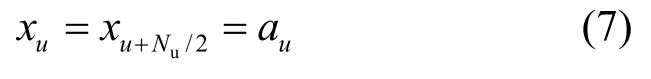
其中，u=1,2,...,Nu/2。

对应的载波映射序列的结构如图3 所示。为更直观地进行展示，频域OFDM 信号波形结构如图4所示。

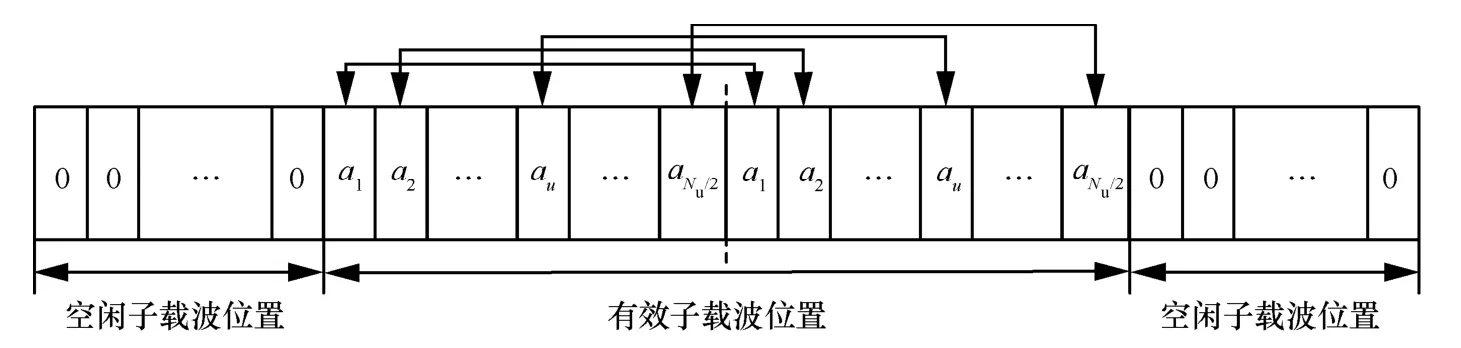
图3 载波映射序列结构

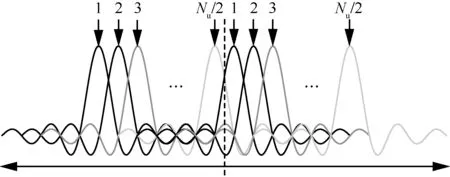
图4 频率OFDM 信号波形结构

由图4 可知，发送端频域OFDM 信号波形中包含对称的两部分，是由图3 中两段相同的星座映射序列一一对应映射到有效子载波上，经过IFFT 之后生成的，这样做相当于面向OFDM 系统子载波实现频率分集，使到达接收端的信号波形具有抗干扰特性。

2) 接收端利用干扰检测和选择合并方法进行干扰抑制

设频域接收信号Y={y1,y2,...,yk,...,yN}，其中yk为第k个载波符号，选取Y中有效载波位置处的信号，其中，为第v个有效子载波符号。接收端经过干扰检测后，得到干扰检测区间I，I∈[Is,Ie]，其中，Is为受干扰程度大的子载波的起始位置，Ie为受干扰程度大的子载波的结束位置，然后在I内对Y′进行选择合并，得到包含Nu/2 个受干扰程度小的有效子载波符号，即可得到最终估计的频域发送信号，其中，表示第i个受干扰程度小的有效子载波符号，通过式(8)得到

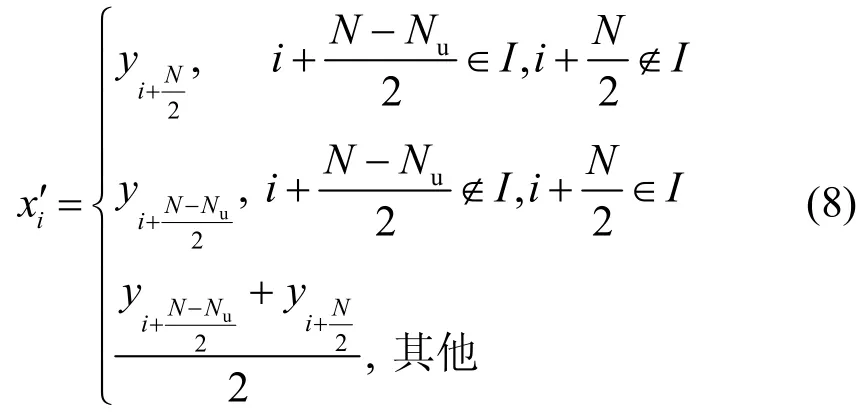
其中，i=1,2,...,Nu/2。

4 性能评估

本节将仿真验证本文提出的基于FCVE 的干扰检测算法及基于频率分集的干扰抑制算法的性能优势。以下仿真中，设OFDM 系统中子载波个数N=256，全为有效子载波，系统带宽为10 MHz，调制方式采用QPSK 调制，编码方式采用1/2 码率的signal to interference ratio）仿真次数为1×106次，仿LDPC编码，单个符号信噪比Es/N0或者信干比（SIR,真采用的信道为AWGN 信道。

4.1 干扰检测

设置符号信噪比Es/N0=0，分别加入单音干扰及部分频带干扰，参考表1，在设置不同的门限因子T条件下，仿真FCME 算法与FCVE 算法的干扰检测性能。

参照2.2 节的部分频带干扰模型，检测概率定义为成功检测到干扰频带边界频点处的次数与蒙特卡罗仿真次数之比，虚警概率定义为将未干扰频带内的有用信号频点检测为干扰频带边界频点的次数与蒙特卡罗仿真次数之比，设置干扰因子r=10%、30%、50%、60%，仿真结果如图5～图8所示。

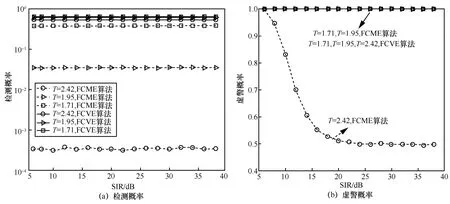
图5 r=10%，FCME 算法与FCVE 算法在不同T 条件下的干扰检测性能

图6 r=30%，FCME 算法与FCVE 算法在不同T 条件下的干扰检测性能

图7 r=50%，FCME 算法与FCVE 算法在不同T 条件下的干扰检测性能

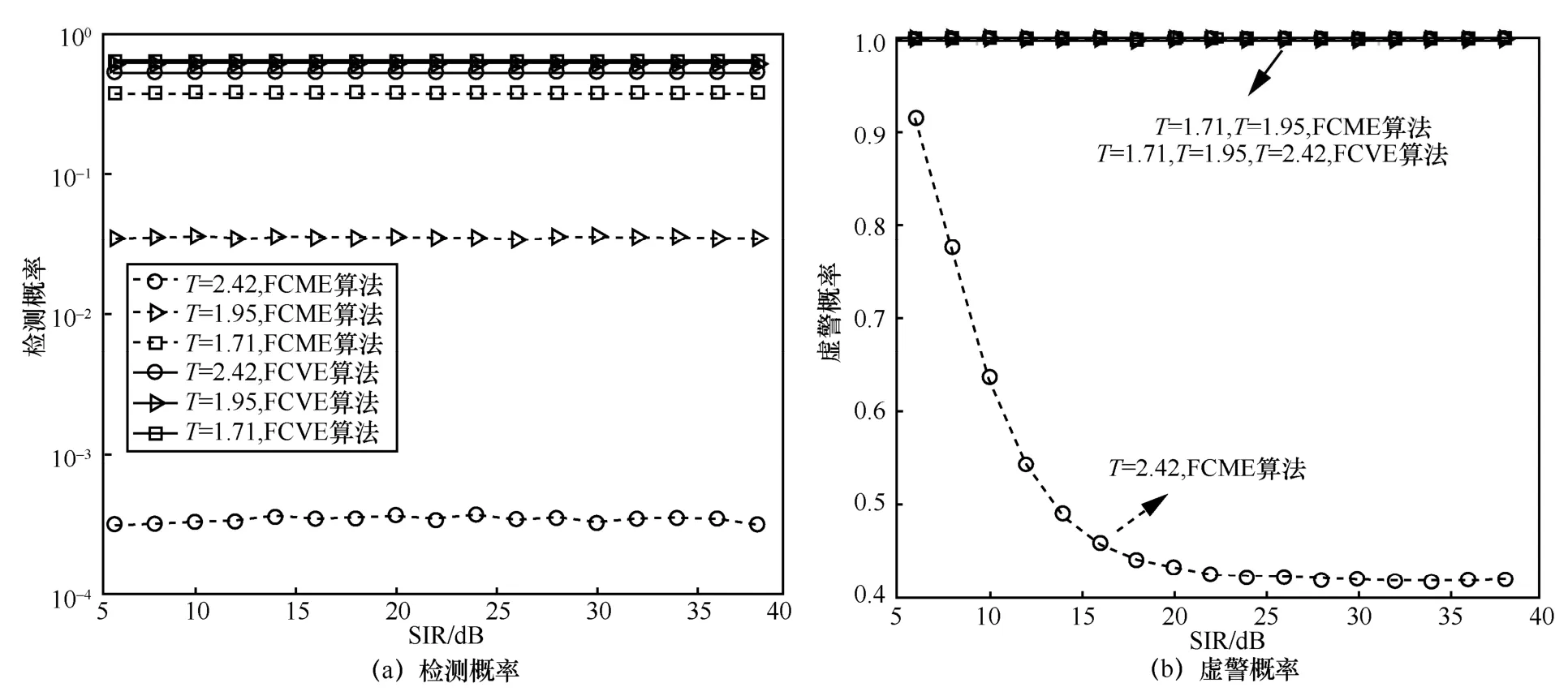
图8 r=60%，FCME 算法与FCVE 算法在不同T 条件下的干扰检测性能

由图5～图8 可以看出，在不同的干扰因子r条件下，FCVE 算法的检测概率明显高于FCME 算法，但以此为代价的是FCVE 算法的虚警概率也更高。

综上所述，FCVE 算法能明显提升检测概率，但同时也具有较高虚警概率。然而，联合下文干扰抑制算法仿真，接收端解调误比特率仍具备较大性能优势。

4.2 干扰抑制

令干扰频偏因子α为单音干扰信号所在频点相对于子载波间隔的归一化频率，设置SIR=-15 dB，仿真对比在不同干扰频偏因子α下的无干扰抑制和频域置零干扰抑制算法[19]的解调BER 性能，其结果如图9 所示。

图9 频域置零算法在不同α 下的BER 性能

从图9 可以看出，在不同干扰频偏因子α条件下，频域置零算法给系统带来了一定的性能增益，但其增益并不明显。因此，频域置零算法虽然简单，但其适用范围有一定限制，一般用于存在频域稀疏性干扰、对系统性能要求不高的场景中。

设置干扰因子r=10%、30%、50%、60%，在无噪环境下对无干扰抑制、频域置零算法以及基于频率分集的干扰抑制算法进行仿真，其结果如图10所示。此外，在有噪环境下，设置SIR=-25 dB、SIR=-20 dB，仿真相应干扰抑制算法的BER 性能，其结果如图11 所示。

图10 无噪环境，在不同干扰因子r 条件下各算法BER 性能对比

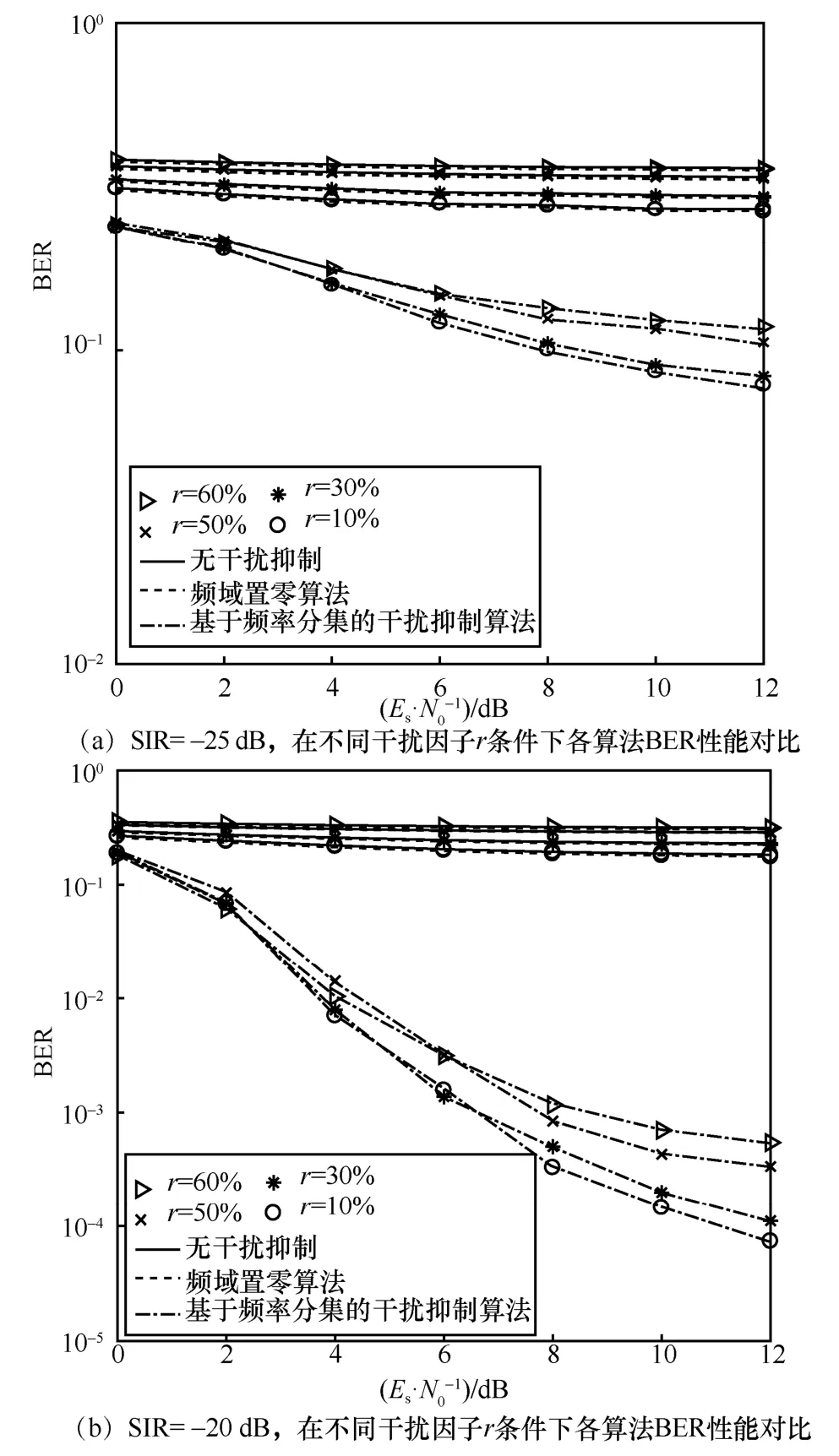
图11 在不同SIR、不同干扰因子r 条件下各算法BER 性能对比

从图10 和图11 可以看出，在不同干扰因子r条件下，本文提出的基于频率分集的干扰抑制算法能够有效抑制干扰，相比于无干扰抑制情况，误比特率性能有较大优势。频域置零算法作为经典的干扰抑制算法，由于其抑制干扰的同时也丢失了有用信号，而且干扰因子越高，有用信息损失越严重，导致干扰抑制性能不佳。因此，频域置零算法常用在窄带干扰的场景中。

5 结束语

本文提出了基于FCVE 的干扰检测算法和基于频率分集的干扰抑制算法。仿真结果表明，在设置相同门限因子条件下，FCVE 算法的干扰检测概率高于传统算法；与无干扰抑制、频域置零算法进行对比，基于频率分集的干扰抑制算法通过简单的实现过程有效提升了系统的干扰抑制性能。需要说明的是，基于频率分集的干扰抑制算法因在发送端面向OFDM 系统子载波实现频率分集，虽然性能优势明显，但降低了系统的频谱效率。在实际应用场景中，干扰功率远强于信号功率，此时保证通信是第一要素，其次才会考虑进一步提升频谱效率，因此，所提算法仍然具有一定的实际应用价值，进一步提升频谱效率也是未来的理论研究目标。