基于DNN 的Sub-6 GHz 辅助毫米波网络功率分配算法

孙长印，刘李延，江帆，姜静

（1.西安邮电大学通信与信息工程学院，陕西 西安 710121；2.西安邮电大学信息通信网络与安全重点实验室，陕西 西安 710121）

1 引言

随着当前蜂窝网络数据需求的迅猛增长，传统蜂窝网络所采用的频段已经无法胜任工作，无线通信系统正向更高的频率发展[1]。毫米波（mmWave,millimeter wave）频段具有丰富的可用频谱资源，可以使无线通信系统实现更大的容量。此外，毫米波还具有速率高、波束窄、能量集中且方向性好等优点，这使毫米波可以成为未来通信系统的主要工作频段。

而对于传统蜂窝网络系统，无线资源的管理是十分重要的，如用户接入、波束形成器设计或发射功率控制[2]等。由于用户间相互干扰产生的非凸性，功率分配问题很难得到最优解[3]。因此，寻找一个次优、高效的解决方案一直是研究的重点。通常功率分配的目标是实现干扰广播信道的加权和速率最大化。为此学者提出了一些经典算法，如加权最小均方误差（WMMSE,weighted mean square error minimization）算法[4]、迭代注水算法[5]和干扰定价算法[6]。虽然这些迭代算法都有不错的性能表现，但是都有较大的时间开销。处理多输入多输出（MIMO,multiple-input multiple-output）干扰系统功率分配问题时，经典算法每一步迭代都需要涉及奇异值分解或者矩阵求逆操作。而信道信息、用户分布等参数都在快速变化，因此此类算法实现实时处理较困难。神经网络的出现为这个难题提供了解决的方案，深度神经网络可以很好地逼近传统迭代算法，并且加快了计算时间[7]。

与传统Sub-6 GHz 频段相比，毫米波的频段的天线尺寸相应较小，有利于移动终端在保持元器件高度集成化的同时，结合大规模MIMO 技术部署更大规模的天线阵列，有效地提高系统的频谱利用率以及抗干扰能力[8-9]。然而，更多数量的天线也意味着波束成形以及信道信息的获取变得更加困难。另一方面，毫米波在空气中传播会被水蒸气、氧气等吸收，导致很大的路径损耗以及随机阻挡。因此，如何对采用毫米波频段的蜂窝网络通信系统进行有效的无线资源管理，以提供稳健高速的链路质量，仍然是一个值得研究的问题。其中毫米波的功率控制问题是亟须解决的。文献[10]研究了在终端直通（D2D,device-to-device）场景下毫米波系统的资源分配与功率控制问题，考虑最大化系统吞吐量，提出了一种基于干扰管理的启发式算法，结合匈牙利算法求出最佳功率分配。文献[11]研究了在毫米波系统的功率控制中应用非合作博弈论，针对毫米波系统中不同的信干噪比门限值的特点，设计了一种新的效用函数，降低了计算的复杂度。考虑毫米波网络的高间歇性，文献[12]利用强化学习模型来预测阻塞状态从而得到功率分配的最优解。与传统通信系统的功率控制算法相同，上述毫米波系统功率控制算法都认为信道信息是已知的，并未考虑毫米波系统的特点，即天线数目多以及覆盖范围小带来的波束搜索开销与盲搜索功耗。

近年来，已经有学者注意到Sub-6 GHz 信号与毫米波信号在到达角、离开角和角度功率谱上存在一致性[13]，而未来的毫米波通信系统可以在多个频段（包括6 GHz 以下和毫米波频段）运行[14-15]。文献[16]将毫米波信道信息的获取转化为压缩感知问题，在Sub-6 GHz 频段提取支撑信息用于辅助毫米波信道估计。基于Sub-6 GHz 和毫米波频段之间的空间相关性，文献[17]研究了毫米波系统中的流量调度算法，使用Sub-6 GHz 链路作为备份以减少毫米波链路容易中断带来的影响。文献[18]提出了在特定条件下从Sub-6 GHz 到毫米波频段存在映射关系，并利用深度学习工具对毫米波波束以及阻塞进行预测。考虑到Sub-6 GHz 信号相对于毫米波信号的传播对阻塞具有更强的稳健性，并且衰减更小，借助一些Sub-6 GHz 信道信息来辅助毫米波系统的运行十分有效。

因此，受已有研究的启发，本文提出基于深度神经网络（DNN,deep neural networks）的Sub-6 GHz辅助毫米波网络功率分配算法，旨在解决毫米波功率控制中面临的3 个问题。首先，毫米波由于覆盖小并且易受遮挡，因此其传输以及功率控制所需的测量都需要波束搜索与跟踪，对于数量众多的天线系统，产生巨大信令的开销；其次，由于毫米波覆盖小，还会导致用户在覆盖范围外时进行盲搜索，使功耗增加；最后，传统功率控制算法需要迭代运算，复杂度高。

本文的主要研究工作如下。

1) 在Sub-6 GHz 与毫米波双频段通信系统中，提出了从Sub-6 GHz 频段信道信息到毫米波频段的最佳功率分配的映射关系。这种确定性映射关系是非线性的，无法从理论上进行显式描述。

2) 利用神经网络模型强大的逼近能力，设计深度神经网络模型用于学习上述映射关系，从而实现使用Sub-6 GHz 频段来预测毫米波频段的最佳功率分配，避免了毫米波特性导致的搜索开销与功耗。

3) 为了验证所提方案的可行性，本文在进行了理论分析的基础上，开展了广泛的仿真实验。结果表明，使用Sub-6 GHz 频段信道信息来辅助深度学习模型预测毫米波频段的功率分配可以在耗时极少的情况下获得较好的性能表现。

2 系统模型

本文考虑如图1 所示的移动通信场景。假设场景下共有K个小区，每个小区每个调度时刻只服务一个用户。基站同时拥有工作Sub-6 GHz 频段以及毫米波频段的均匀线性阵列（ULA,uniform linear array）天线，天线数目分别为Tsub-6和TmmW。移动端在Sub-6 GHz 频段以及毫米波频段都使用单天线进行通信。Sub-6 GHz 频段的天线采用纯数字结构，用于上行信令及业务传输，以及进行信道估计。毫米波天线则选用纯模拟设计，主要考虑下行数据传输[19]。

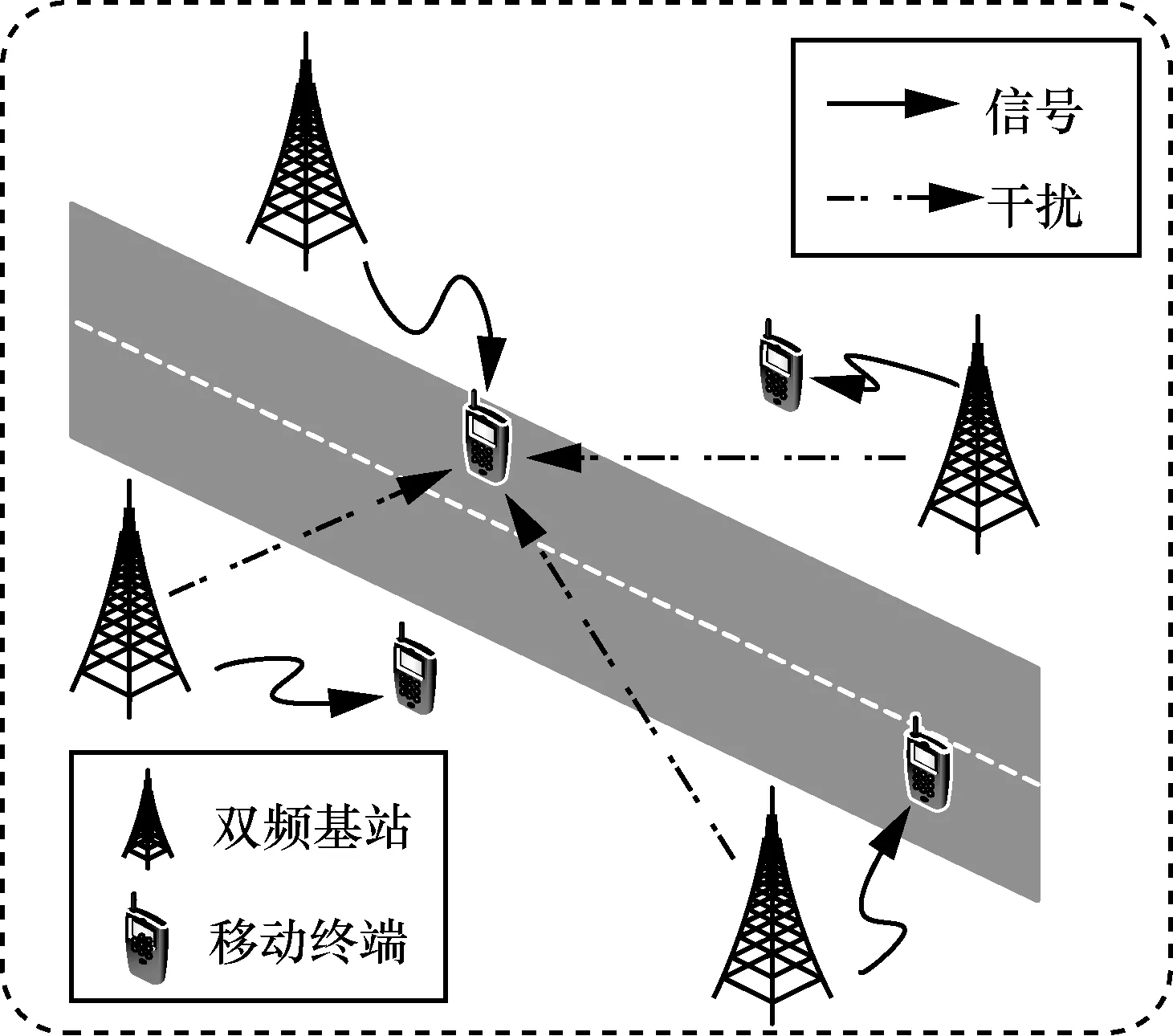
图1 移动通信场景

设ik表示第k个基站服务的用户i，用表示用户i到基站k的Sub-6 GHz信道矩阵。则基站接收到用户ik上行信号可以表示为

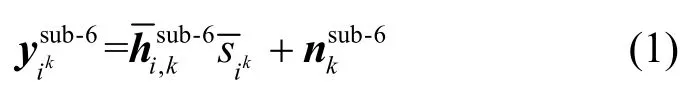
为了降低毫米波链路的路径损耗，使用基于码本的波束赋形方案。若表示波束成形向量，表示从基站k到用户ik的毫米波频段信道矩阵，那么移动端接收到的下行毫米波信号可以写为

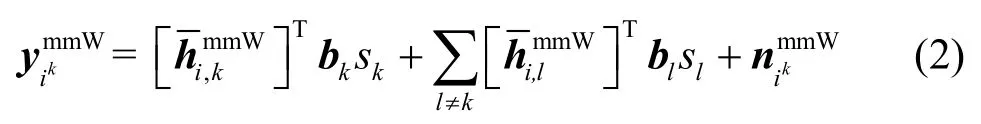
其中，波束成形向量bk从包含N组候选波束成形向量的量化码本B中选取，sk为基站k试图传输的符号，表示用户ik接收到的噪声。

用户ik处毫米波频段的信干噪比可以表示为

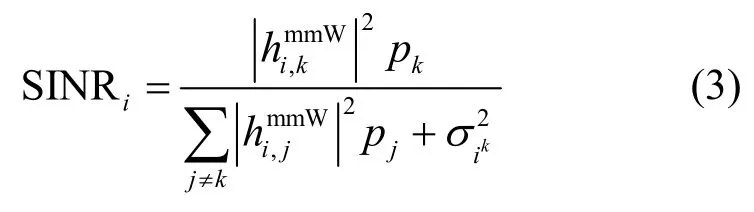
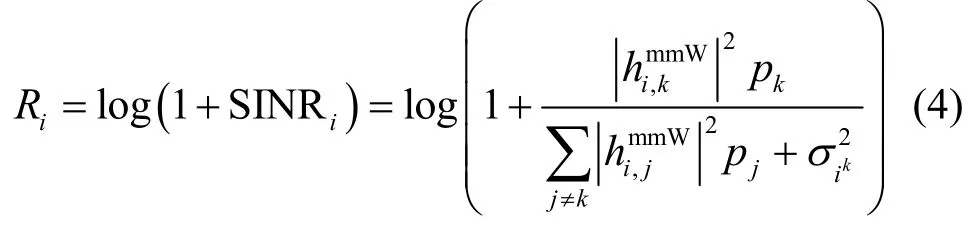
其中，0≤pk≤Pmax，Pmax为发射机的最大传输功率。

本文考虑加权和速率最大化为目标的功率分配问题求解。令P={p1,p2,···,pK}表示用户的功率分配矢量。表示所有用户经过波束赋形后的下行毫米波信道增益。则系统中所有用户的加权和速率可以表示为

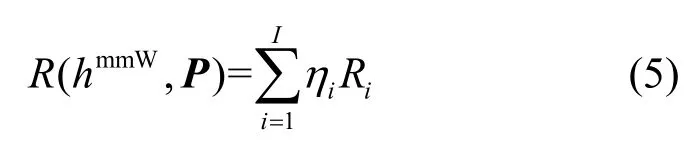
其中，ηi＞ 0为用户的优先级。而系统的加权和速率最大化问题可表示为

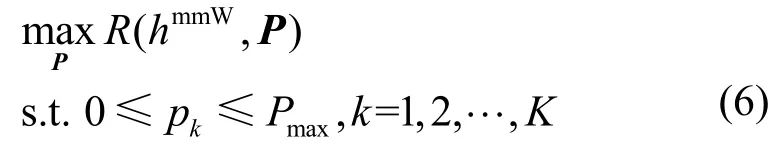
那么，用户的最佳功率分配为

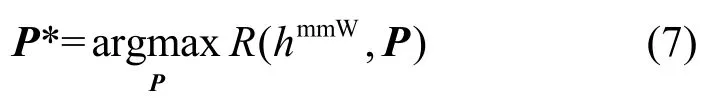
此时，系统的加权和速率可以取得最大值Rmax。

由于式(3)中各小区功率相互偶合，系统加权和速率最大化变为NP-hard 问题[20]。传统的求解算法是将问题转化为求次优解，往往通过迭代实现，复杂度较高。此外，传统的功率控制算法单独依赖于下行信道信息，当获得下行信道信息比较困难时，如在双频段毫米波通信系统中，将无法实现功率实时控制。

3 Sub-6 GHz 辅助毫米波网络功率分配

本节将双频段系统中毫米波网络功率分配问题分3 个部分进行论述。首先，提出了在特定的条件下存在Sub-6 GHz 的信道数据到毫米波频段的最佳功率分配的确定性映射。然后，对WMMSE 算法进行简化，并且用于产生毫米波频段的最佳功率分配。最后，得到从Sub-6 GHz 信道到毫米波频段最佳功率分配的复合映射，并且证明可以使用神经网络学习这种映射关系，从而预测毫米波频段的功率分配。

3.1 将Sub-6 GHz 信道映射到毫米波最优功率分配

首先，对图1 所示的双频段毫米波通信系统场景，假设基于量化码本的波束搜索，分别得到每个用户2 个频段信道增益矢量hsub-6与hmmW。若以Si表示任意用户ik的位置，表示用户ik所有位置的集合。那么，对于用户ik，可以定义以下2 种从位置到信道增益的映射函数。

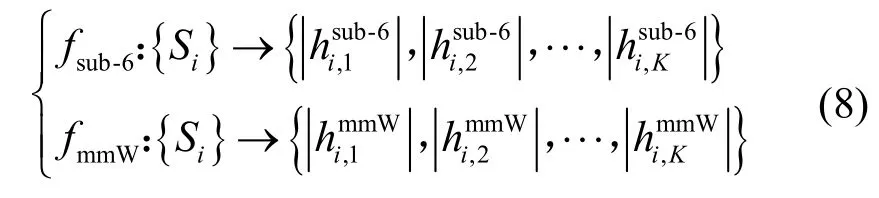
假设1fsub-6是双射。

通常情况下，由于天线的数目和阵列形状、信号传播路径以及环境等因素的影响，映射fsub-6是双射的概率非常高[21-22]。若fsub-6是双射，那么它的逆映射的存在性也是本文后续进行推广的基础。

更进一步地，考虑到系统中的多个用户，使用S={S1,S2,···,SI]表示当前所有用户的位置分布，则可以将上述2 个映射扩展为

不难看出，gsub-6(·) 与gmmW(·)只是fsub-6(·)与fmmW(·) 的简单叠加。因此，映射gsub-6(·)也存在逆映射。在此基础上可以进行简单的推导，在映射中隐去用户群位置S可得

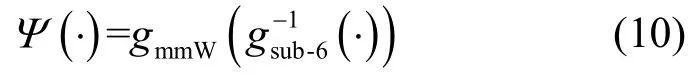
从而得到所有用户的Sub-6 GHz 信道增益到毫米波信道增益的映射为

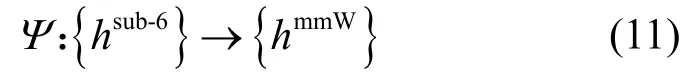
在本文设定场景下，结合式(6)，可以得到下行毫米波信道加权和速率最大化问题如下

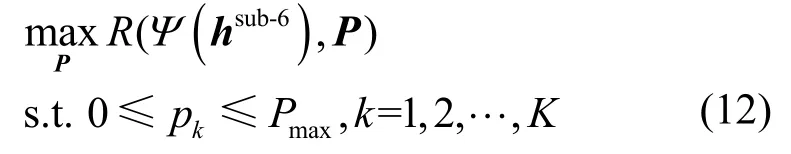
而下行毫米波信道的最佳功率分配可以描述为

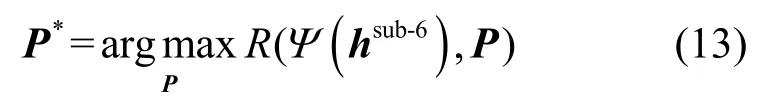
3.2 WMMSE 算法

WMMSE 算法最初是为了设计线性波束形成器而提出的，其后被推广到其他的和效用最大化问题[4]。本文对其进行调整，以利于用DNN 和Sub-6 GHz 预测的毫米波信道功率分配P*。

本文假设双频段都完成波束搜索，故下行毫米波信道可以近似看作一个单输入单输出的多小区干扰信道模型。则用户ik接收到来自基站k的信号可以表示为

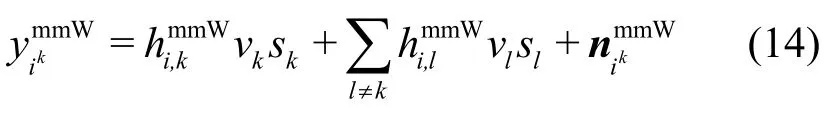
其中，vk表示基站k的波束增益，表示用户ik处的噪声。用户接收到的传输符号可以写为

其中，uk表示用户ik处的接收机波束形成增益。假设传输符号与噪声之间相互独立，那么用户ik处传输符号的均方误差为

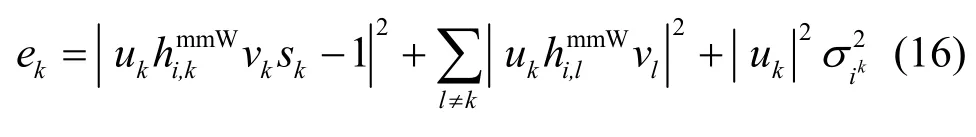
根据式(16)，下行信道的加权均方误差最小化问题可以表示为

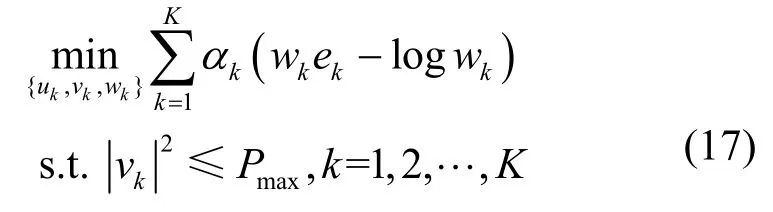
其中，wk为正的权重系数；为了便于计算，使用αk代替前文中ηi表示的基站k服务的用户ik的优先级。

式(6)与式(17)已被证明是等价的[4]，式(17)可利用块坐标下降的方法进行求解。算法详细的迭代步骤如算法1 所示。

算法1加权最小均方误差功率分配算法

输入

步骤1算法初始化

设定t=0；随机初始化发射端增益

步骤2迭代计算

循环以下过程，直至t等于设定循环次数

1) 迭代次数更新t=t+1

3.3 基于DNN 的功率分配算法

尽管上文已经通过式(13)给出了Sub-6 GHz 频段的信道信息与毫米波频段的最佳功率分配之间的关系，但仍然不能直接通过普遍近似理论[23]来证明此关系可以被神经网络学习。虽然3.2 节给出了使用毫米波信道增益来计算P*的算法，但在通常情况下式(6)的解不是唯一的，为了使从hsub-6到P*存在一个确定的映射，本文提出了假设2。

假设2由算法1 计算出的毫米波功率分配矢量P*满足R(hmmW,P*)＞R(hmmW,P),∀hmmW，并且P*≠P。

假设2 意味着对于任意给定的hmmW都只存在唯一的P*使下行信道和速率达到Rmax。若存在R(hmmW,P*)=R(hmmW,P**)=Rmax，P*≠P**的情况，无论是选取P*或P**都对系统和速率有同样的贡献。因此，不妨认为假设2 在本文设计的场景中成立。

那么，可以将从hsub-6到P*的连续映射定义为

根据普遍逼近定理[23]，使用ΓN(·)表示单个隐藏层有N个神经元构成的的密集神经网络的输出，那么对与连续的功率映射函数Ω(·)以及任意给定的误差ε＞ 0，都存在一个足够大的正整数N满足

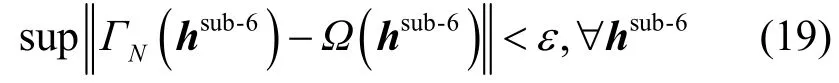
因此，本文可以通过神经网络模型来对这种隐式的映射进行学习，从而实现利用Sub-6 GHz 频段的信道信息预测毫米波信道最佳功率分配的目的。值得一提的是，虽然可以使用单个隐藏层对这种连续的映射进行逼近，但经过验证，较好的预测性能表现仍然需要多个隐藏层。

4 神经网络模型与参数设定

4.1 网络结构

本文选择使用包含一个输入层、多个隐藏层以及一个输出层的全连接神经网络来逼近功率映射函数Ω(·)。神经网络模型的输入层包含IK个节点，输入为Sub-6 GHz 频段的信道增益{hsub-6}；输出层包含I个节点，输出为计算得到的毫米波信道功率分配{P*}。在隐藏层选用ReLU 作为激活函数为神经网络引入非线性因素。特别地，考虑到发射机最大功率的约束条件，输出层设计了带约束的激活函数如下

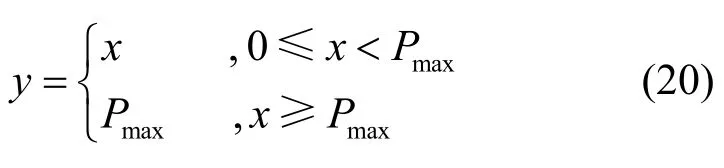
代价函数选择使用每一个用户的预测功率分配pk与标签之间均方误差的加权和

表1 总结了训练神经网络过程中的具体参数。

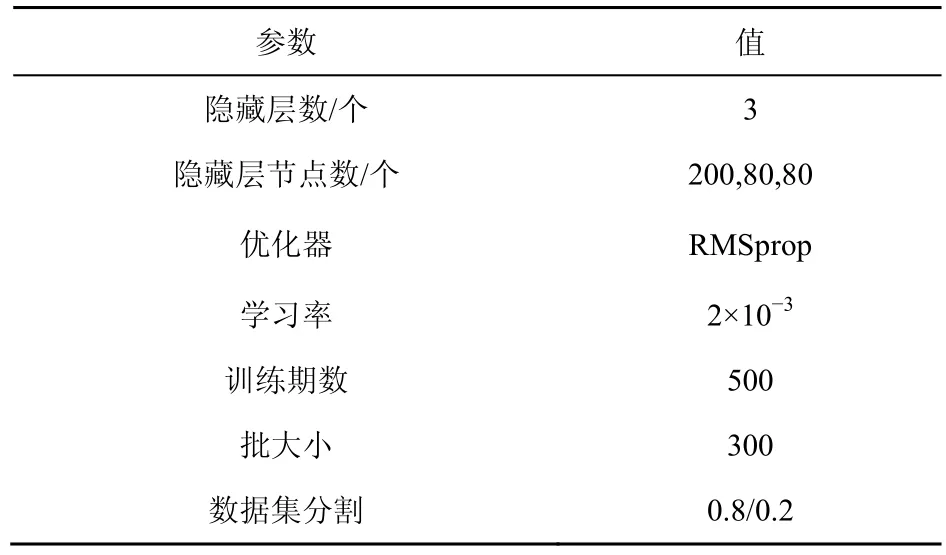
表1 神经网络参数

4.2 数据集选取

由于实际信道数据的获取受限，工程中常采用基于射线追踪的方法生成信道数据。本文使用的数据来自3D 射线追踪软件构建的Deep MIMO 数据集[24]。此数据集中的双频段通信场景O1 包含28 GHz 的毫米波基站数据集O1_28 以及3.5 GHz的6 GHz 以下基站数据集O1_3p5。

本文所提神经网络模型采用非在线训练模式，可以大幅减少在线计算所需要的开销。首先，通过文献[24]中的脚本来分别生成双频段信道矩阵集合∀i,∀k。考虑到当使用Sub-6 GHz信道矩阵作为神经网络输入时，输入层神经元规模将十分庞大，本文利用波束搜索方案将Sub-6 GHz信道矩阵转变为信道增益，大幅减少输入层的节点个数。其次，神经网络的输出，即毫米波频段的功率分配矢量{P*}，由经过波束成形后通过算法1 生成。最后，将每一组用户分布对应的Sub-6 GHz 频段的信道增益矢量与毫米波频段功率分配矢量组合起来，得到数据集中的样本，其中n为样本索引。

4.3 场景设定

基于非在线的训练模式，本文选取了以下3 种场景以检验所提算法的有效性以及性能。场景1 与场景2 神经网络模型的训练是独立的，仿真参数汇总在表2 中，其中部分参数采用文献[18]。

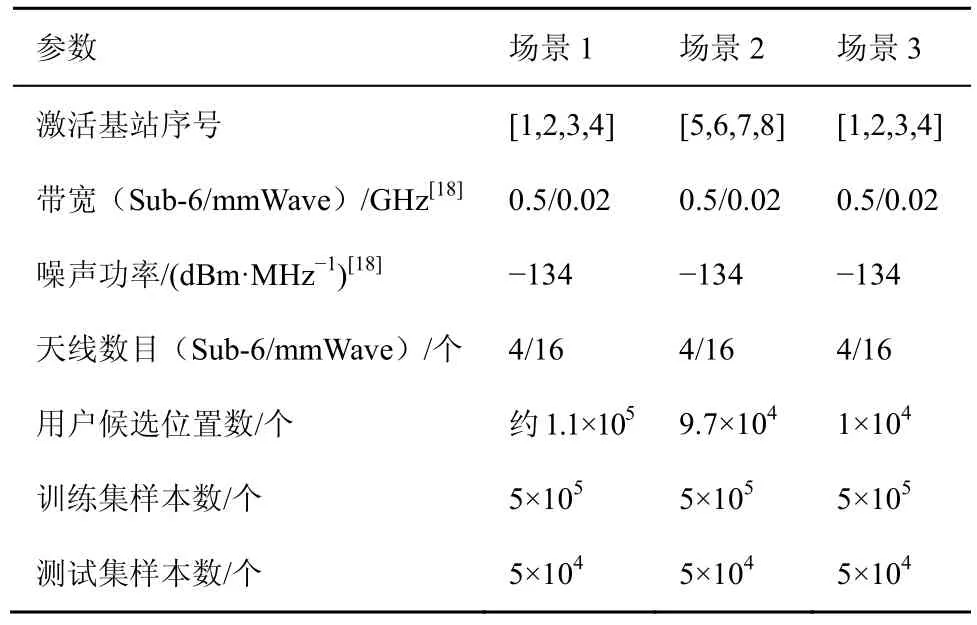
表2 仿真参数

场景1主街道场景。场景1 是一条主街道的一部分，模拟用户在单条街道步行的情景。在街道两侧对称分布着4 个具有双频段天线的基站，用户均匀分布在整个区域。每次都在候选用户集中为4 个小区分别随机选取一个用户作为服务用户，每个用户被选取的概率相同。

场景2交叉路口场景。此场景选取2 条主街道的交叉部分，模拟用户在经过交叉路口时的情景。4 个基站分布在街道角落的内侧，可以覆盖到均匀分布在整个区域的所有用户。数据集生成准则同场景1。

场景3主街道-边缘场景。此场景内基站和用户分布都与场景1 相同，区别在于用于测试神经网络模型的用户分布样本是在小区覆盖的边缘区域生成的。设计此场景的目的是验证用户身处小区覆盖边缘的情况下，所提算法预测的功率分配是否同样有效。

5 仿真结果与分析

5.1 可行性验证

为了检验使用Sub-6 GHz 信道增益预测毫米波信道的功率分配的有效性，本文设计了相应的方案：当2 个频段同时使用单天线进行通信时，在场景1 和场景2 下分别使用2 个频段的信道增益作为神经网络输入，毫米波信道的功率分配作为神经网络输出来训练网络，并在测试阶段对100 000 组样本和速率分布情况进行评估，仿真结果如图2 和图3 所示。

通过分析图2 和图3 可以看出，在2 个场景下使用Sub-6 GHz 信道增益（简称为Sub6-DNN）与直接使用毫米波信道增益（简称为mmW-DNN）来预测样本的毫米波频段功率分配所得到的和速率分布结果基本一致。即使是场景2 中某些分布存在和速率接近为零的情况，所提Sub6-DNN 也能与mmW-DNN 预测结果保持一致。

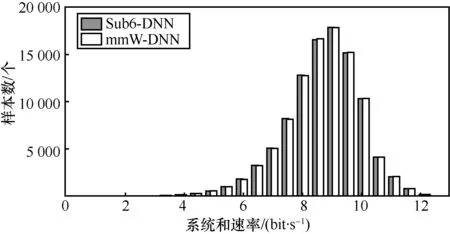
图2 场景1 单天线收发的和速率分布

表 3 列举了 Sub6-DNN、mmW-DNN 和WMMSE 算法所得所有样本的平均和速率。在不同的场景下，Sub6-DNN 的预测结果虽略逊于mmW-DNN，但仍可以十分接近WMMSE 算法的性能表现。这些结果验证了使用Sub-6 GHz 信道预测毫米波频段功率分配的能力。

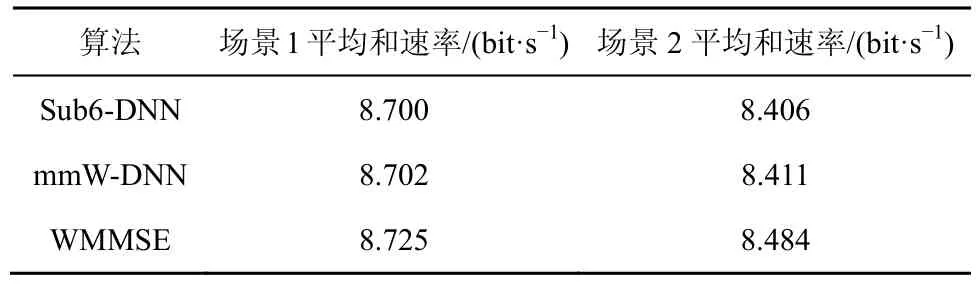
表3 神经网络与WMMSE 算法性能对比（单天线）

此外，考虑到mmW-DNN 需要使用毫米波信道的原始数据训练网络，但毫米波信道测量会有很大的开销与功耗，而使用Sub-6 GHz 的信道信息可以避免这个问题，因此在性能表现相近的情况下选择使用Sub-6 GHz 信道预测毫米波频段功率分配性价比更高。

5.2 预测性能表现

在场景1 与场景2 下，基站双频段都使用多个天线进行收发（采用表2 中的数据）。使用上文中的神经网络模型针对2 个场景分别进行训练，并在测试阶段选用最大功率分配与随机功率分配方案进行对比。所得功率分配计算出系统和速率并绘制出累积分布曲线如图4 与图5 所示。

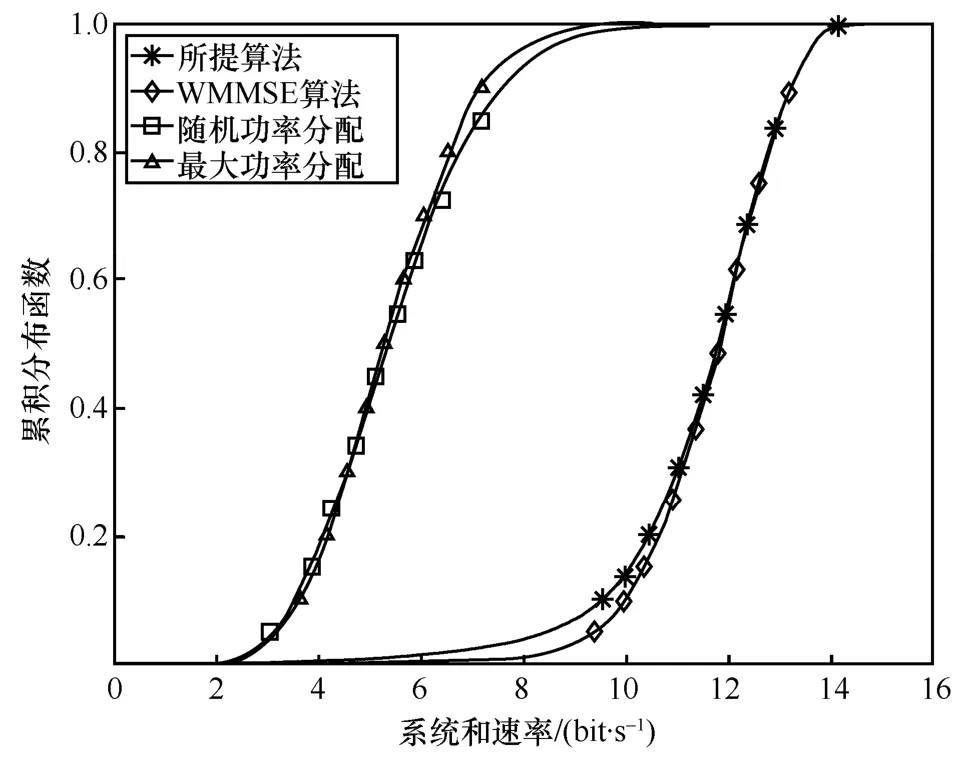
图4 场景1 不同算法和速率分布

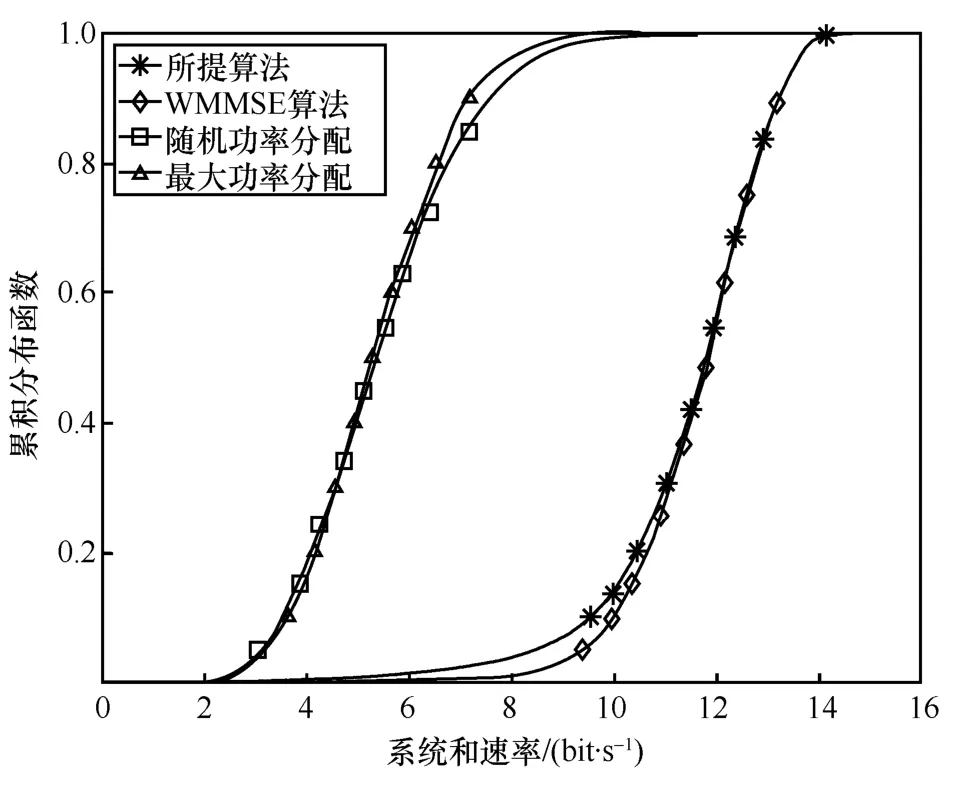
图5 场景2 不同算法和速率分布

如图4 所示，在场景1 下，最大功率分配与随机功率分配算法所得样本的和速率集中分布在区间[2,10]，样本和速率小于9 bit/s 的概率为1。而所提Sub6-DNN 与WMMSE 算法预测结果均分布在区间[4,14]，明显优于最大功率分配与随机功率分配算法。虽然，所提算法预测的结果约有40%的样本和速率分布在区间[4,12]内，和速率略小于WMMSE算法，但多数样本和速率大于12 bit/s，预测结果与WMMSE 算法所得高度一致。

与图4 类似，图5 展示了场景2 下4 种算法的样本和速率对比。最大功率分配与随机功率分配算法所得样本的和速率集中分布在区间[1,8]，也明显劣于Sub6-DNN 与WMMSE 算法。不同的是，所提 Sub6-DNN 只有约 40%的样本预测结果与WMMSE 算法保持一致，分布在大于12 bit/s 的区间，而在场景1 下有约60%。

虽然已经证明了可以通过神经网络模型对WMMSE 算法进行无限逼近，但通过仿真可以看出，对于部分和速率较低的样本，所提算法表现略差于WMMSE 算法。若要继续减少所提算法的与WMMSE 算法的差距，需要继续增加神经元或隐藏层的数量。

为了综合对比本文Sub6-DNN 与WMMSE 算法的性能，在表4 与表5 中列举了2 种算法分别对不同场景下测试集的50 000 组样本进行功率分配的耗时以及平均和速率。结果表明，所提Sub6-DNN在2 种场景下均可以在耗时少于WMMSE 算法的0.1%的情况下，获得不小于97%的和速率性能。

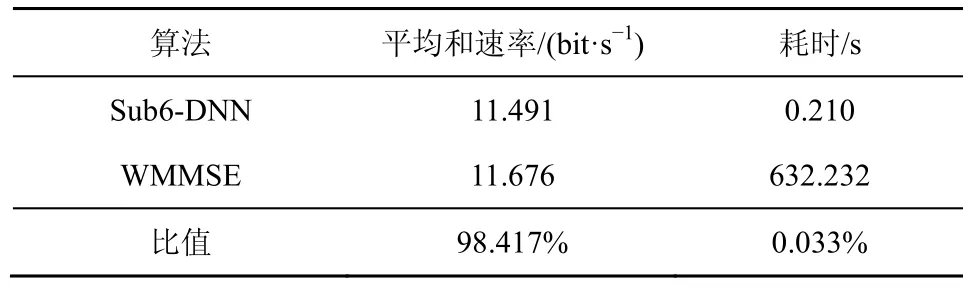
表4 算法性能表现对比（场景1）

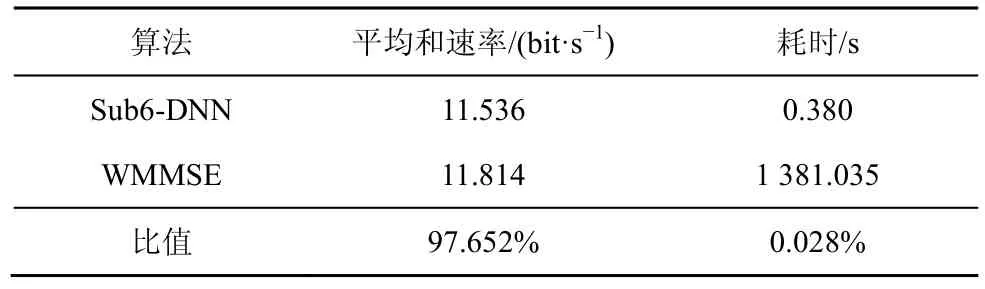
表5 算法性能表现对比（场景2）

而对于场景3 的边缘分布用户，同样使用已经在场景1 下训练好的神经网络模型进行测试，结果如图6 所示。在未对数据集进行优化之前，所提Sub6-DNN 所得样本的和速率虽然远优于最大功率分配与随机功率分配算法，但与WMMSE 算法在整个和速率区间上都有不小的差距。这是由于训练集中边缘用户分布样本较少导致了少数样本的预测性能表现不佳。

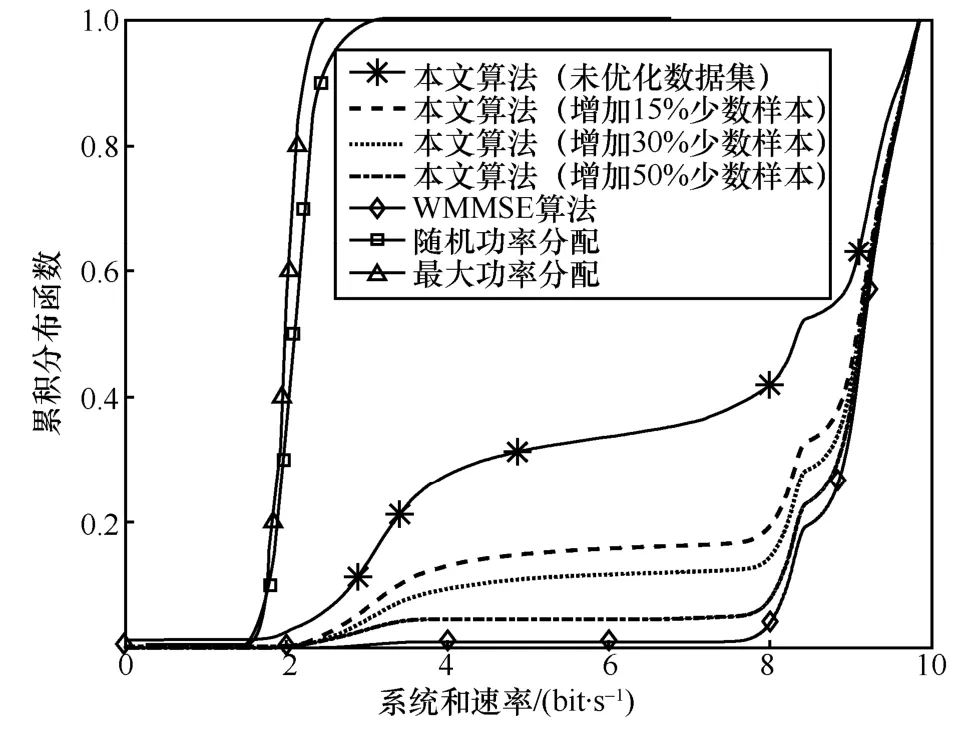
图6 场景3 和速率表现对比与数据集优化影响

这种数据集样本分布不均衡的现象在实际应用中非常常见，会对神经网络的性能造成一定影响。处理这种不平衡数据集的方案一般分为2 种：算法级优化与数据级优化。算法级优化通常在分类问题中使用，通过调整分类边界来提高算法对少数类样本的敏感性。这种优化方案无法直接引入功率控制问题，因此本文考虑数据级优化方案对数据集进行处理。

最简便的数据级优化方案是增加数据集中少数类样本的数量，这也是最有效的解决方案。例如，考虑到实际情况中样本获取比较困难，文献[25]借助对抗生成网络（GAN,generative adversarial network）来对少数类样本进行数据增广，获取新的少数类样本，同样可以提高数据集中少数类的占比。此外，在训练时对数据集进行不同方式的采样，也可以缓解数据集的不均衡问题。

通过图6 可以看出，向原数据集中添加不同占比的少数分布样本之后，所提算法的性能得到了不同程度的改善。当向原数据集中添加15%的少数分布样本时，和速率分布在区间[2,8]的样本占比减少了大约50%。当添加的少数分布样本占比增加到30%时，和速率分布在小于9 bit/s 的样本占比进一步减少。而当增加少数分布样本占比达到50%时，所提算法性能已经远超于未对数据集进行优化时，非常逼近WMMSE 算法。

5.3 稳健性评估

考虑到实际中信道测量通常会有噪声与误差存在，这会造成经过测量得到的信道信息不准确。本节考虑基于随机扰动模型的信道估计误差[26]，研究信道测量误差对算法性能的影响。具体来讲，在测试集数据中为每个用户的Sub-6 GHz 频段信道矩阵叠加零均值，方差为的高斯噪声，其中，α为误差指数，用于模拟信道测量误差。然后，通过训练好的神经网络对带有不同误差指数的测试集数据进行测试。使用WMMSE 算法计算无信道估计误差时的系统和速率，并将其作为本文所提算法预测结果的上界。

图7 表明了在场景1 下，尽管输入神经网络模型的Sub-6 GHz 频段信道信息出现偏差，本文所提算法表现仍然相对较好，这也突出了使用Sub-6 GHz信道有效预测毫米波信道功率分配的稳健性以及对信道变动的适应性。而用于对比的最大功率分配算法与随机功率分配算法因为不需要信道数据，和速率不随信道测量误差变化。

图7 各算法平均和速率与误差指数的关系

此外，通过将功率分配二值化，即pk=0或Pmax，可以在一定程度上提高预测精度，改善算法性能[7]。对于本文所提算法，在误差指数小于10-3时，使用二值化功率分配为样本的平均和速率带来了约0.3 bit/s 的提升，在一定程度上提高了神经网络的预测性能。但随着误差指数的增加，这种提升也逐渐减小，最终与未经过二值化的预测结果保持一致。这是由于信道测量误差较大时，二值化所带来的和速率提升远小于网络输入存在偏差带来的负面影响。这也侧面反映了在实际通信场景中，对信道信息的准确掌握是有效进行实时功率控制的前提。

6 结束语

为了在毫米波通信系统中实现实时高效的功率控制，本文首先提出了从Sub-6 GHz 信道到毫米波信道最佳功率分配的映射函数。然后，利用普遍逼近理论，证明了可以通过神经网络模型来对此映射函数进行学习，从而预测毫米波最佳功率分配。为此，本文设计了一个神经网络模型，利用Sub-6GHz 信道来执行预测任务，并且根据DeepMIMO数据集对神经网络模型进行了评估与测试。结果表明，所提神经网络算法在开销极小的情况下，具有良好的预测性能。