图神经网络的标签翻转对抗攻击
2021-09-28吴翼腾刘伟于洪涛
吴翼腾,刘伟,于洪涛
(信息工程大学,河南 郑州 450002)
1 引言
对抗攻击指有目的地对输入数据施加微小扰动,以使学习模型输出错误的预测结果[1]。本文认为与对抗攻击直接关联的研究可上溯至20 世纪70 年代的统计诊断[2]。统计诊断最早研究了学习模型的微小扰动对统计推断带来的影响。近年来,随着深度学习的发展,其应用安全受到广泛关注。Szegedy等[3]研究图像数据的卷积神经网络(CNN,convolutional neural network)安全问题时提出了“对抗样本”概念[4]。Zügner 等[5]提出处理图数据的深度学习模型图神经网络(GNN,graph neural network)的对抗攻击。
图神经网络对抗攻击研究正处于快速发展阶段,相关研究成果活跃于国际学术会议[6-8]。分析最新研究成果发现,当前研究存在扰动类型不足、前提假设单一等问题。现有研究的扰动类型通常仅考虑增删节点和连边;攻击假设通常仅基于矛盾数据假设,具体说明如下。
1) 扰动类型不足。现有图神经网络对抗攻击的扰动类型[9-10]主要是特征扰动、增删连边和节点注入[5,11-13],没有考虑将训练数据中的特定样本标签翻转为其他类别导致模型预测错误的标签翻转攻击。标签翻转攻击已被其他数据类型的对抗攻击场景广泛研究。例如,统计诊断[2,14]的经典模型均值漂移模型和局部影响分析模型[15-17]都详细研究了因变量扰动对模型统计推断的影响,是标签翻转攻击的最初形式。张宏坡等[18]提出了一种基于熵值法的标签翻转攻击方法,来评估朴素贝叶斯分类器对标签噪声的稳健性。Muñoz-González 等[19]实现了针对深度神经网络的标签翻转数据投毒攻击。文献[20]针对基于图的半监督学习模型(区别于图神经网络)建立了统一的标签翻转攻击架构。然而,针对图神经网络的对抗攻击还未见标签翻转攻击这种扰动类型。
2) 前提假设单一。现有图神经网络对抗攻击通常仅基于矛盾数据假设建立攻击模型,而未考虑攻击前后模型训练参数的显著差异以及测试数据和训练数据分布的一致性。本文基于以下3 种攻击假设展开研究。①文献[5,8-9,13,21]将投毒攻击建模为寻求扰动方法,在训练集上构建一组存在矛盾的训练数据,使重训练的图神经网络在训练集上的损失最大,以降低测试数据预测准确率。本文将现有攻击方法概括为基于矛盾数据假设的攻击方法。②矛盾数据假设不能很好地对过拟合攻击场景建模。本文受统计诊断[2,14,22]研究工作的启发,引入参数差异假设,即“有效攻击前后图神经网络训练参数应该具有较大差异”的假设建立攻击模型。③对抗攻击方法忽视了机器学习最基本最常见的前提假设——同分布假设,即“随机划分的训练集和测试集应该具有相同分布”的假设。
本文基于3 种攻击假设分别建立图神经网络的标签翻转攻击模型,以期在不同数据分布条件下分析图神经网络对标签噪声的敏感性和潜在安全漏洞。图神经网络应用广泛,它不仅应用于节点分类、图分类、链路预测等复杂网络任务,也可应用于文本分类、关系抽取等自然语言处理任务,还可应用于图像分类、目标检测等计算机视觉任务。在上述应用中,图神经网络的训练数据通常需要人工收集和标记,实际应用中多采用众包技术收集和标记数据。该收集和标记方式成本低廉且方便快捷;但无法充分保证标签质量,进而导致数据中存在不可避免的标签噪声,影响图神经网络的学习过程[18],更无法避免精心设计的投毒数据。鉴于此,图神经网络标签翻转攻击的研究意义是从攻击者的角度研究标签翻转攻击,可以预知图神经网络在各项任务中的安全威胁,评估图神经网络对标签噪声的敏感性,为标签噪声的检出和过滤、设计稳健的图神经网络提供理论基础。本文主要工作如下。
1) 针对图神经网络对抗攻击扰动类型不足的问题,提出评估图神经网络对标签噪声稳健性的标签翻转对抗攻击方法。
2) 针对图神经网络对抗攻击前提假设单一的问题,首先基于经典的矛盾数据假设建立标签翻转攻击模型;然后引入参数差异假设和同分布假设,建立标签翻转攻击模型。
3) 理论分析证明了在一定条件下,基于同分布假设模型的攻击梯度与基于参数差异假设模型的攻击梯度相同,从而建立了2 种攻击方法的等价关系,进一步增强了模型攻击机理的可解释性。
4) 实验对比分析了3 种基本假设对应的损失度量在标签翻转攻击中的优势和不足;大量实验验证了标签翻转攻击模型的有效性。
2 基本概念
图表示为G(V,E),其中,V为节点集合,E为连边集合。设节点数|V|=N,则无权无向图可用对称的邻接矩阵A={0,1}N×N表示,AT=A。图中每个节点有n维特征向量,节点特征用矩阵X={0,1}N×n表示。文献[23-25]将图神经网络简化为SGC(simple graph convolution),它具有低通滤波器的作用。本文以SGC 为攻击和研究对象。SGC 模型的表达式为

其中,Yout为SGC 模型输出,A为滤波矩阵,X为输入特征向量,W为参数矩阵。在文献[25]中,A的形式通常为
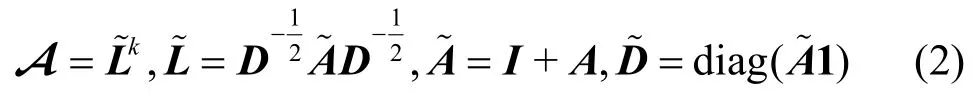
其中,I为单位矩阵,1表示元素全为1 的列向量。设Z=XA,记softmax(·)为σ(·),Y表示one-hot编码的标签矩阵。使用交叉熵损失函数,并将其表达为矩阵形式为

本文研究非指定目标、标签翻转的数据投毒攻击。非指定目标攻击不指定具体的一个或几个攻击目标,需要使测试集整体的预测准确率下降;标签翻转攻击允许将特定的训练样本标签翻转为其他类别;投毒攻击允许图神经网络对投毒的训练数据重新训练,使重训练的图神经网络在测试集的预测准确率下降。
3 标签翻转对抗攻击模型
3.1 基于矛盾数据假设的攻击模型
文献[5,8-9,13,21]建立了连边扰动的图神经网络投毒攻击模型。按上述文献定义,攻击方法可以统一概括为以下约束优化问题

其中,A为原始邻接矩阵,为扰动后的邻接矩阵,为矩阵中非0 元素的个数,δ为扰动开销,W*为扰动后得到的训练参数。投毒攻击允许对参数重新训练,是双层优化问题。
从上述投毒攻击的统一形式化表述中可以看出,现有攻击方法都是构造扰动后的样本数据,使图神经网络在扰动后数据集上损失函数达到最大,即图神经网络不能很好地拟合扰动后的训练集,扰动后的训练集中存在矛盾的训练数据。根据上述分析,现有方法可概括为基于“有效攻击的训练集中存在矛盾的训练数据”假设(简称矛盾数据假设)的攻击方法。
基于矛盾数据假设,图神经网络的标签翻转攻击模型可以表述为以下约束优化问题
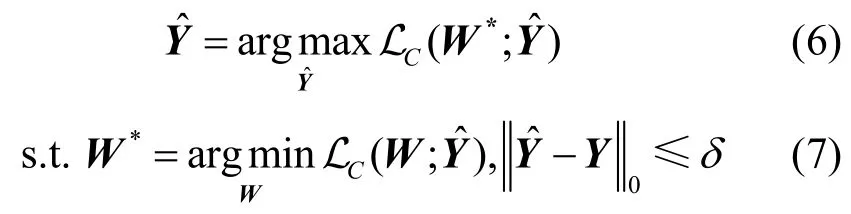
3.2 基于参数差异假设的攻击模型
受统计诊断学科启发,基于“有效攻击前后图神经网络模型参数应该具有较大差异”的假设(简称参数差异假设),本文建立图神经网络的标签翻转投毒攻击模型,可表示为如下约束优化问题
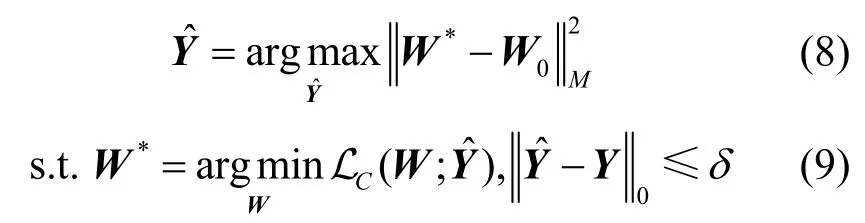
为衡量参数差异,从统计诊断经典文献[2,14-17,22,26]中引入Cook 距离作为度量攻击前后的参数差异。
定义1Cook 距离。参数矩阵*W与W0的Cook距离CD 定义为
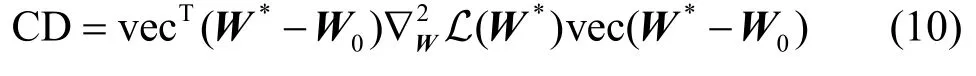
其中,vec(·)表示矩阵按列优先拉直为列向量。
图神经网络通过优化求解算法求得使损失函数L 达到最小值的参数矩阵W0,即W0满足∇WL(W0)=0。实用中∇WL(W0)≈0。对∇WL(W)在W*处进行一阶泰勒展开并取W=W0得
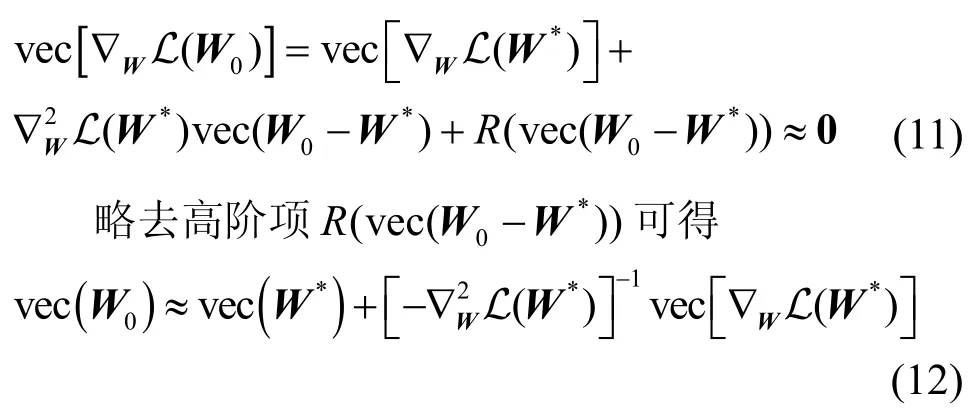
基于以上分析,衡量参数差异的Cook 距离可近似表示为
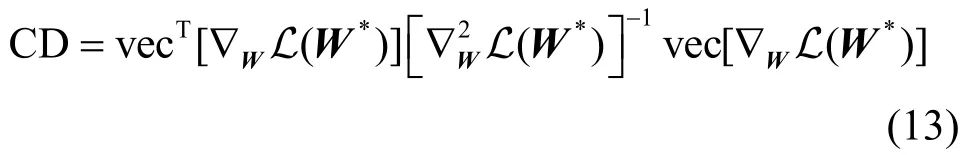
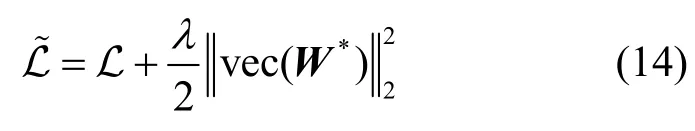
容易求得

其中,I是与同型的单位阵。此时可逆。基于此,修正后的Cook 距离~CD 表示为
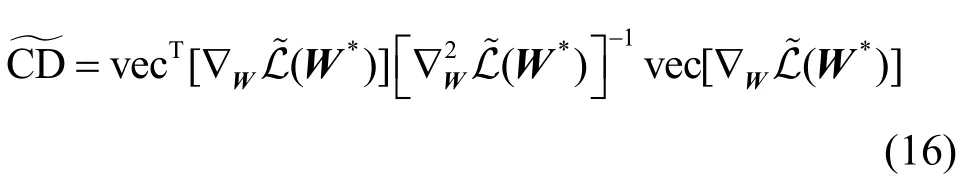
攻击模型可以表示为
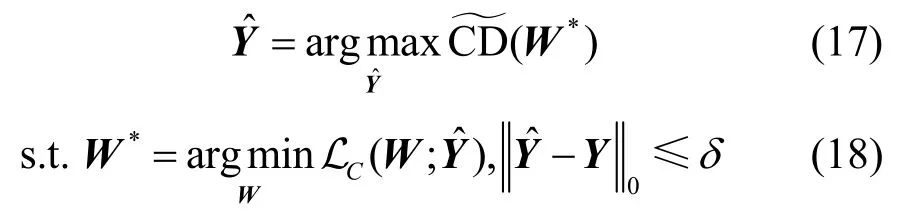
基于参数差异假设的攻击模型同样分为投毒攻击和对抗训练2 个阶段。在式(17)所示的投毒攻击阶段,使用修正后的Cook 距离作为损失函数;在式(18)所示的对抗训练阶段,训练数据为扰动后的训练数据,因此与基于矛盾数据假设的损失函数相同。
3.3 基于同分布假设的攻击模型
图神经网络对抗攻击问题忽略了一种机器学习最基本、最常见的前提假设,即同分布假设。无论图神经网络还是其他深度学习或机器学习方法,通常首先基于同分布假设展开研究,即认为训练集的数据分布与测试集一致,因此这些方法可以在训练集中学习数据模式,并有效地迁移至测试集。分析实际攻击场景,投毒攻击的目的是通过污染训练数据,使其训练的图神经网络在未污染的测试集上的错误率(损失函数)达到最大。若考虑训练测试集的同分布假设,相应的攻击模型应该改为通过污染训练数据,使其训练的图神经网络在未污染的训练集上的错误率(损失函数)达到最大。
根据以上分析,基于“随机划分的训练数据和测试数据对于图神经网络模型应该具有同分布性质”的假设(简称同分布假设),建立标签翻转投毒攻击模型,可表示为如下约束优化问题
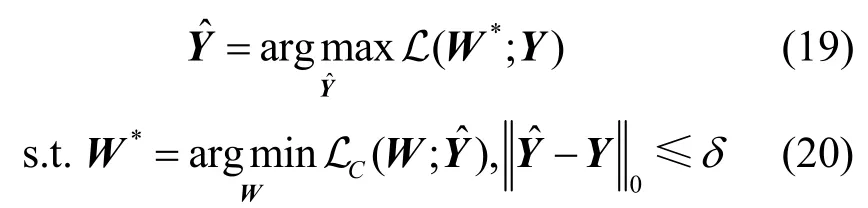
根据3.1 节和3.2 节分析,无论何种攻击模型,在对抗训练阶段均采用扰动后的训练数据,因此式(20)与式(7)、式(18)相同。基于同分布假设的攻击模型在投毒攻击阶段,使用式(3)的交叉熵作为损失函数。从形式上,基于同分布假设的攻击模型与基于矛盾数据假设的攻击模型的差异仅体现在损失函数式(6)和式(19)中,式(6)使用扰动后的标签矩阵,式(19)使用未扰动的标签矩阵。但二者的建模思想是不同的。本文3.4 节将证明,在某些较弱的条件下,基于同分布假设的攻击模型与基于参数差异假设的攻击模型等价。
3.4 攻击梯度及其等价定理
本节介绍上述攻击模型的符号记法,主要涉及L、LC、之间的区别。L 由式(3)定义,L 代入的标签矩阵Y为未扰动的标签矩阵;LC由式阵;由式(14)定义,为带有正则项的L。Cook距(6)定义,LC代入的标签矩阵为扰动后的标签矩离CD 由式(13)定义;由式(16)定义,表示由~L定义的Cook 距离CD。
设图神经网络(1)采用梯度下降法训练
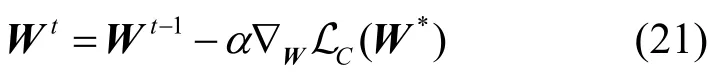
经过t=t0轮训练,可得模型的训练参数。具体地,可求得损失函数对参数的梯度为
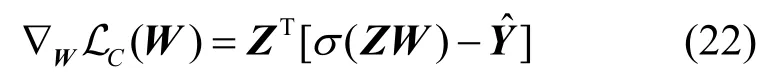
代入式(21),有
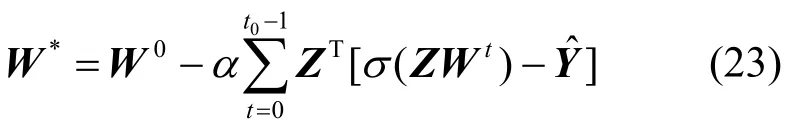
对于离散的标签矩阵Y,优化问题式(6)、式(17)、式(19)属于NP 难问题。现有文献主要依据攻击梯度实施扰动。攻击梯度是实现有效攻击的主要依据。
从攻击梯度的角度,定理1 给出了参数差异假设与同分布假设的等价性。
定理1设

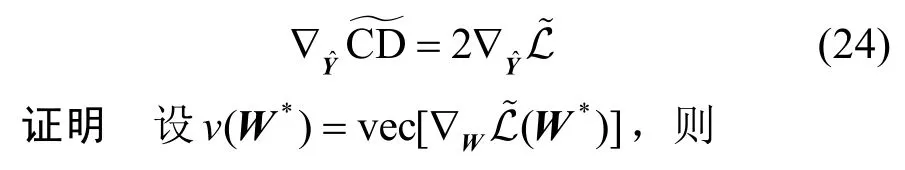
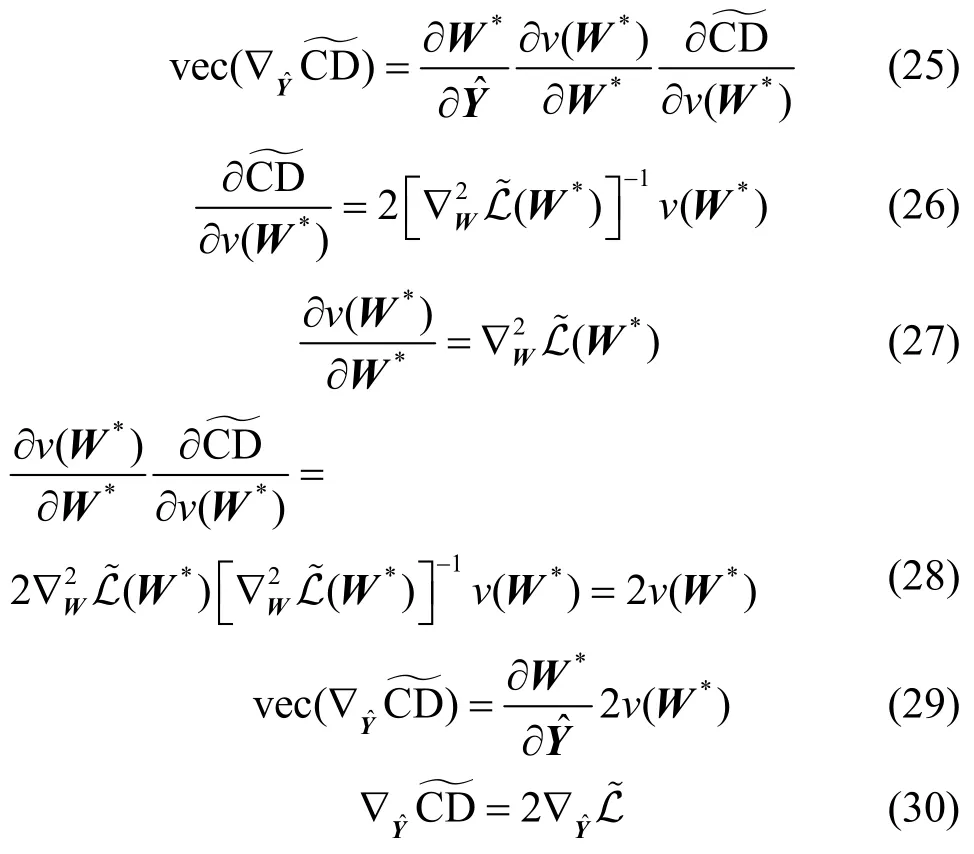
证毕。
定理1 表明,衡量参数差异的Cook 距离的攻击梯度与基于同分布假设攻击模型的攻击梯度相同,因此从攻击梯度的意义上,上述2 个模型等价。从而说明基于同分布假设的攻击方法的物理意义也是诱导图神经网络训练出一组异于原始参数的训练参数。
直接从基于同分布假设的损失函数出发,也可定性分析得出相同的结论:攻击后式(19)的损失函数L 增大,但攻击前后损失函数中Y、A、X保持不变,仅参数*W发生改变,表明攻击前后图神经网络的训练参数具有较大差异。该结论解释了文献[13]中提及但未从理论上证明的实验现象。
矛盾数据假设为
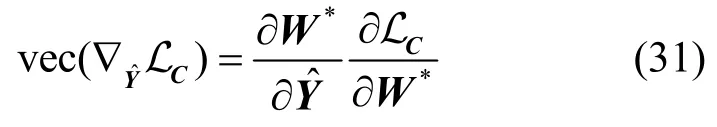
参数差异假设为

同分布假设为
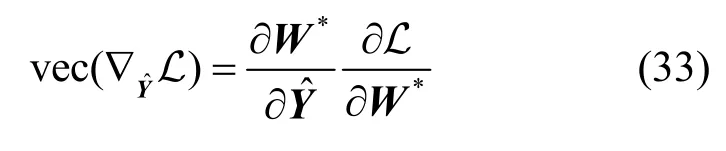
3.5 攻击算法
根据上述分析,以及式(31)~式(33)求得的攻击梯度,采用贪心算法实施扰动,可设计图神经网络的标签翻转对抗攻击算法如算法1 所示。
算法1标签翻转对抗攻击算法
输入邻接矩阵A,特征矩阵X,标签Y,攻击点数n
输出扰动列表disturb_list

4 实验
4.1 对比实验
实验采用型号为TITAN Xp 的GPU 显卡,运行环境为ubuntu 16.04 系统、cuda10.0、Python3.6 以及Pytorch1.4。实验采用的数据集为Polblogs[29]、Cora_ml、Cora[30]、Citeseer[31],数据集的统计特性如表1 所示。由于现有研究尚未考虑标签翻转攻击,将所提3 种标签翻转攻击方法与随机翻转标签攻击方法Random 以及2 种经典的连边扰动投毒攻击方法Mettack[13]和Min-max[32]进行对比实验。Mettack采用approximating meta-gradients[13]。Min-max 的攻击方式设置为negative cross-entropy[32]。本文提出的标签翻转攻击方法参数设置与Mettack 保持一致。具体地,对于数据集Polblogs、Cora_ml,图神经网络SGC 正向训练的学习率取α=0.1;对于数据集Cora、Citeseer,学习率取α=0.01。式(2)中SGC 模型幂指数为k=1 和k=2。Mettack 和Min-max 攻击方法允许对训练集中连边总数的5%进行攻击,并控制扰动后的节点度不超过原始网络中节点度的最大值;标签翻转攻击方法Random、LC、L 允许对训练数据中5%的标签翻转至其他类别。基于参数差异假设的标签翻转攻击模型正则项λ=0.001。实验划分数据集中40%为训练集,60%为测试集,数据集随机划分20 次,记录20 次SGC初始准确率平均值和攻击后准确率平均值,实验结果如表2 所示。表2 中准确率的最小值用黑体标出。
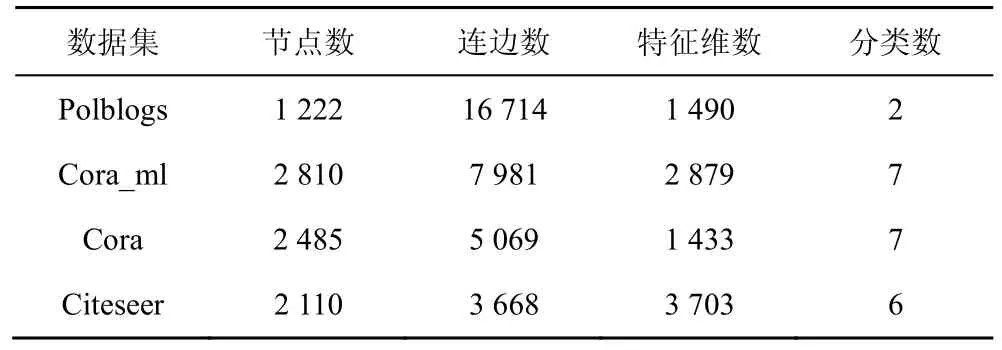
表1 数据集统计特性
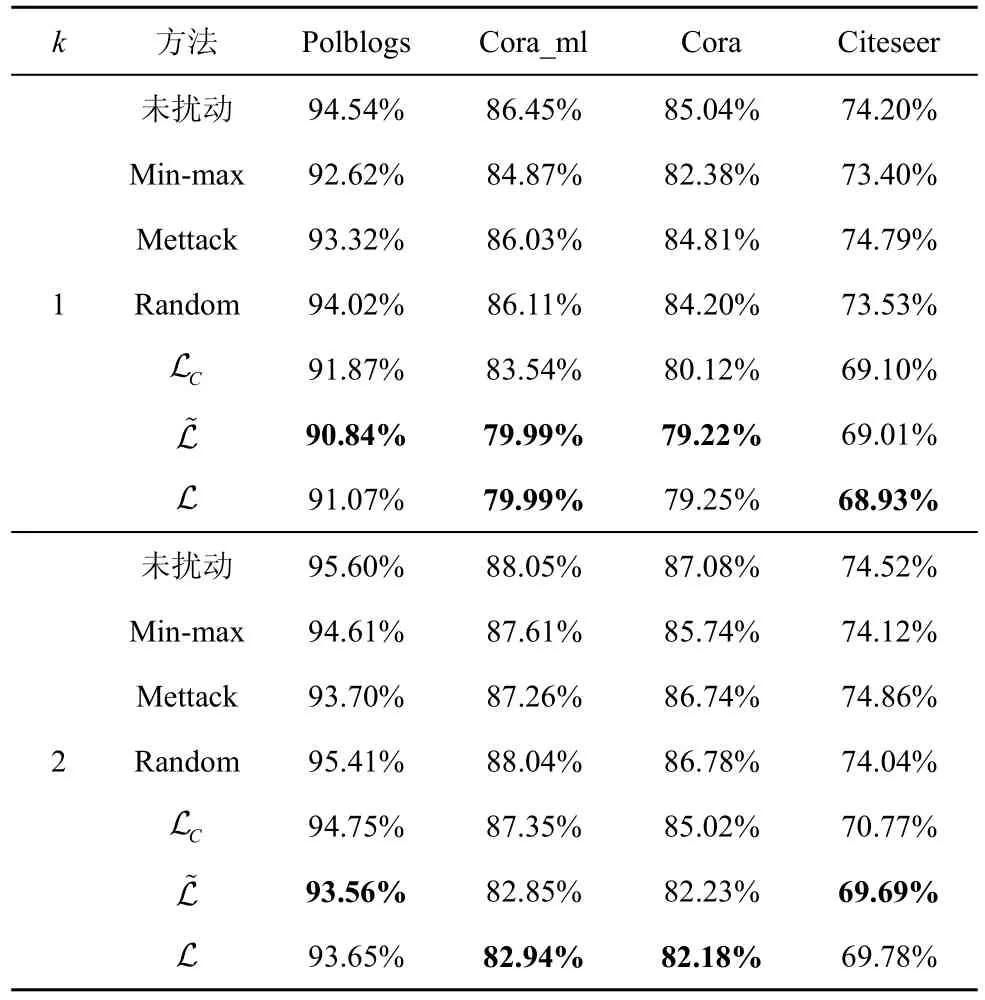
表2 准确率
综合分析以上数据,可以得出如下结论。
1) 考虑标签翻转攻击类型,可以实现有效的投毒攻击。在相同扰动比例比较基准下,基于3 种假设的标签翻转攻击效果优于基于 Mettack 和Min-max 方法的连边扰动攻击效果。实验结果证明了标签翻转这一新的攻击类型的有效性。
2) 对于标签翻转攻击,随机翻转标签几乎无法实施有效攻击。对于5%的扰动,图神经网络SGC的预测准确率没有明显下降,表明通过式(5)重训练,图神经网络可以抵抗随机攻击。而针对本文所提的投毒加扰方式,SGC 的预测准确率下降明显。这种恶意注入的标签噪声可能在数据标记阶段产生,图神经网络在实用中存在潜在威胁。该标签噪声同时具有不易察觉性,将在4.2 节分析。
3) 对于本文提出的3 种标签翻转攻击方法,本文条件下的实验结果表明,基于参数差异假设和同分布假设的标签翻转攻击模型的攻击效果优于基于矛盾数据假设的攻击效果。基于参数差异假设的攻击效果几乎与基于同分布假设的攻击效果相同,与等价性定理得出的理论结果一致。
表2 列出了5%的扰动各攻击方法的攻击结果。为进一步比较不同方法的攻击效果,说明扰动量对攻击效果的影响,其他实验条件不变,采用1%~10%的扰动并记录准确率下降的平均值。选取标签翻转攻击方法Random、LC与L(的实验结果与L 类似),实验结果如图1 所示。
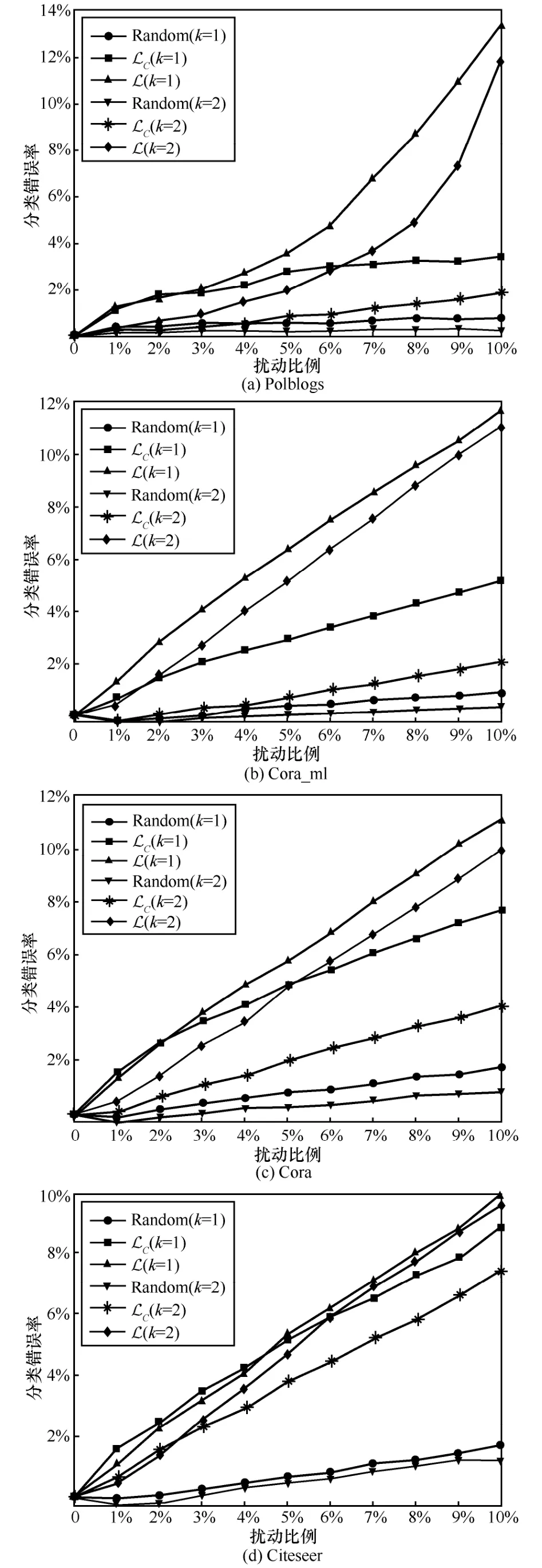
图1 不同扰动量的攻击效果对比
总体而言,基于矛盾数据假设和同分布假设的攻击方法相比于随机翻转标签攻击有更明显的攻击效果。随机翻转标签攻击无法抵抗图神经网络重训练。无论k=1 和k=2,基于同分布假设的攻击效果均优于基于矛盾数据假设的攻击效果,具体原因将在4.3 节详细分析。实验结果说明了本文所提出的基于不同假设的标签翻转攻击模型的有效性和攻击假设的合理性。
4.2 扰动的难以分辨性分析
本节从图结构统计特征[33]和标签类别分布两方面分析标签翻转攻击的难以分辨性。
1) 图结构统计特征。标签翻转攻击不对图结构实施扰动,图结构的各项统计特征例如度分布、节点特征相似度、模体等局部结构特征均保持不变。
2) 标签类别分布。图2 绘制了Cora_ml 数据集k=1时原始标签分布和4种标签翻转攻击方法扰动后的标签分布(图2 随机选取20 次实验中的某次实验结果作为示例)。其他数据集的实验结果与之类似,实验结论相同。
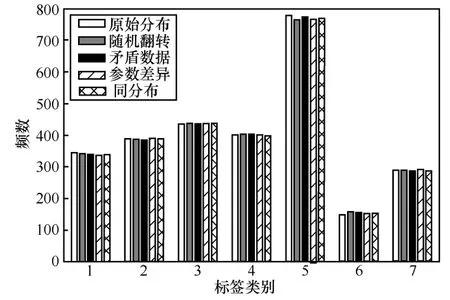
图2 标签类别分布对比
观察标签类别分布可知,扰动后各类别标签分布与原始标签分布差异不大。若实际场景中需严格保持标签类别分布不变,只需对攻击算法中的扰动筛选策略稍作调整。例如,不仅依据攻击梯度大小次序筛选扰动元素,而且限定后一轮攻击翻转至前一轮的原始标签类别。如此迭代,可保持标签类别分布不变。或者,基于前文实验证明的随机翻转标签无法实施有效攻击的结论,为保持标签类别分布不变,投毒攻击后再采用随机扰动平衡标签分布(简称随机平衡策略)。基于随机平衡策略,得到Cora_ml 数据集k=1 时基于矛盾数据假设LC和同分布假设L 的实验结果如图3 所示(的实验结果与L 类似)。图3 中同时对比了4.1 节不使用该策略的实验结果。可以看出,加入随机平衡策略的攻击结果仍然具有可用性,与原攻击效果差异不明显。
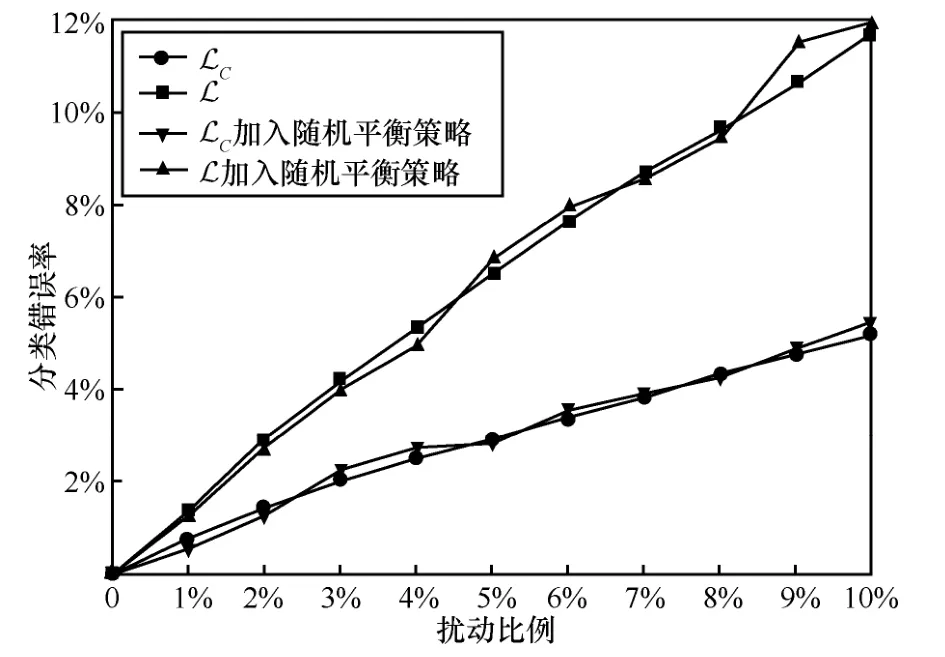
图3 加入随机平衡策略实验结果对比
4.3 模型的比较分析
本节详细分析矛盾数据假设、参数差异假设与同分布假设及相应损失函数的合理性,并与随机翻转标签进行对比分析。实验记录各方法在扰动量为1%~10%下的训练准确率和测试准确率;对每种攻击方法(包括随机攻击Random)均同时计算3 种损失函数值,即 LCL(随机攻击方法没有专门的损失函数,只计算随机扰动后其他3 种损失函数值)。实验设置与4.1 节相同,所有数值均为20 次实验的平均值。选取数据集Cora_ml 的实验结果如表3 和表4 所示。其他数据集和不同参数下的实验结果与所列结果相似。综合分析表3 和表4 的数据,可得出以下结论。
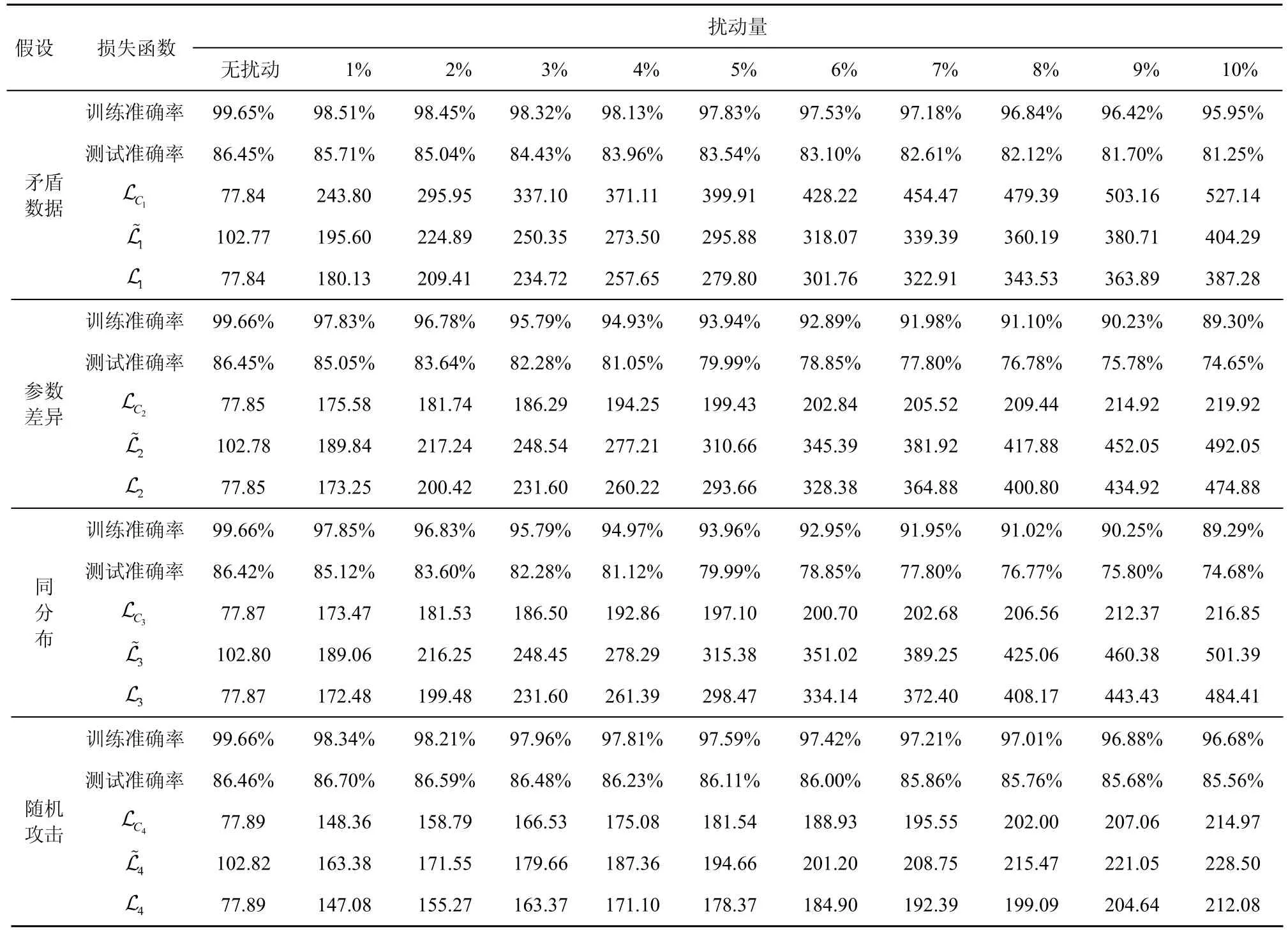
表3 k=1 时数据集Cora_ml 基于不同假设的比较分析
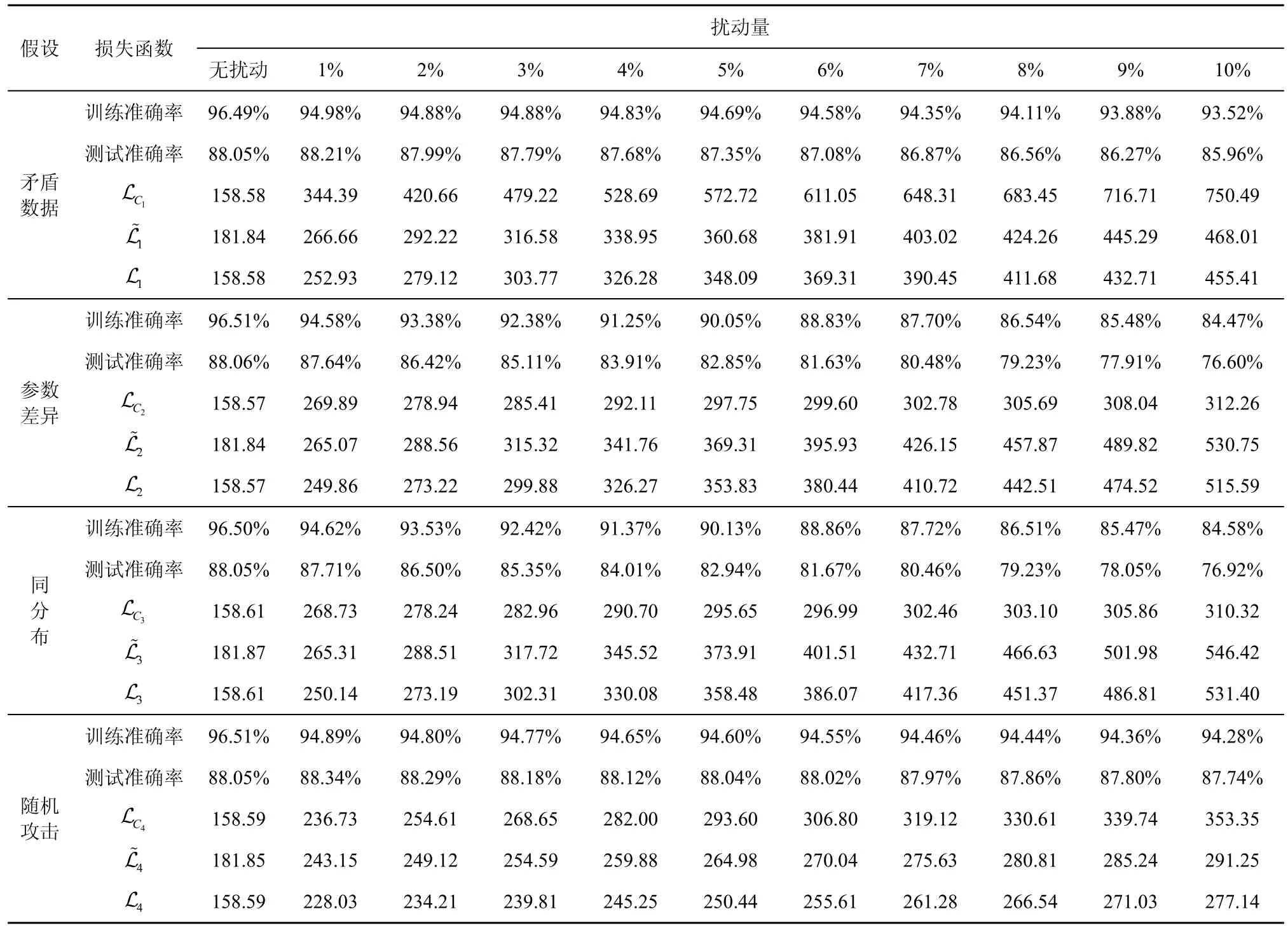
表4 k=2 时数据集Cora_ml 基于不同假设的比较分析
1) 基于3 种假设建模的损失函数具有有效性。对于未受扰动的原始数据,4 种攻击方法对应的基于矛盾数据假设的初始损失函数值和基于同分布假设的初始损失函数值L1、L2、L3、L4相同,当k=1 时,约为77.85;当k=2 时,约为158.60。由于未对数据进行投毒扰动,标签矩阵Y与相同,且初始参数*W相同,因此损失函数值相同。基于参数差异假设的初始损失函数,当k=1 时,约为102.78;当k=2时,约为181.85。因为基于参数差异假设的损失函数与其他二者相比添加了正则项,导致损失函数的初值不同。基于3 种假设的标签翻转攻击方法均表现出随着扰动量的增加,训练测试准确率递减、损失函数递增的趋势,证明了基于3 种假设建立损失函数的有效性。而对于随机翻转标签攻击方法,随着扰动量增加,损失函数虽有上升趋势,但上升并不明显,尽管扰动量达到10%,依据参数差异或同分布损失L 来衡量,损失函数值也达不到基于3 种假设攻击方法3%的扰动损失,而扰动后的准确率大致处于基于3 种假设攻击方法1%扰动量的攻击效果,随机翻转标签的攻击效果不理想。
5 结束语
标签翻转对抗攻击在统计诊断、垃圾邮件检测、图像中的对抗样本以及基于图的半监督学习等领域得到了广泛研究。本文针对图神经网络对抗攻击扰动类型不足的问题,提出并实现了图神经网络的标签翻转对抗攻击。首先,提炼出对抗攻击有效性机理的矛盾数据假设、参数差异假设和同分布假设。然后,基于3 种假设建立攻击模型并实验验证。有效攻击的核心是基于攻击假设建立攻击模型进而求解攻击梯度。攻击梯度是实施有效攻击的主要依据。为保持标签扰动的不易察觉性,可增加限制条件保持标签分布不变,这容易通过修改扰动筛选策略来实现。本文得出以下结论:1) 对于处理图数据的深度学习模型图神经网络,标签翻转对抗攻击具有有效性;2) 采用基于梯度的攻击方法,参数差异假设与同分布假设建立的攻击模型等价;3) 本文场景中基于参数差异假设和同分布假设的标签翻转攻击方法优于基于矛盾数据假设的攻击方法。
由于实际场景中某一样本难以界定唯一的归属类别,或样本本身存在错误标注,这可能大幅降低图神经网络模型的预测能力,因此标签翻转对抗攻击研究为图神经网络的模型诊断和稳健的图神经网络设计提供了必要前提。后续研究工作可基于标签翻转攻击原理,对图数据中的异常点、强影响点、离群点等进行检测和模型诊断,从而改善数据质量;并设计图神经网络结构,建立能够防御对抗攻击干扰的稳健图神经网络。
