基于聚类分析的滑动时均序列需水预测优化方法

2021-09-28桑学锋常家轩李子恒

中国农村水利水电 2021年9期

刘鑫，桑学锋，常家轩，李子恒

（1.华北水利水电大学水利学院，郑州450046；2.中国水利水电科学研究院，水资源管理研究室，北京100038）

作为粤港澳大湾区的核心引擎，深圳是一座充满活力和创新力的新型大都市，流动人口是深圳的显著特征。深圳也具有很好的营商环境，孕育出华为、平安、招商、腾讯等一批具有国际竞争力的企业，创业密度位于全国前列，吸引了很多人员来深圳就业。

但是深圳本地水资源匮乏，全市无大江大河。小河流虽然多分布广，但干流短，河流径流量小，导致水库自产水量少，因此，深圳供水主要依靠境外引水，每年境外引水量约为地表水供水量的85%。受年度引水指标限制，取水量有限，再加上广东省供水压力的逐年增长，深圳每年的引水指标一直受到广东省政府的限制。而水源单位在上报下一年度的用水计划时无法有效预测下一年的需水，导致上报数据质量较差，这也导致年度引水计划无法有效制定。因此，能够准确预测每个水厂及行政区的需水情况将对深圳制定年度引水计划具有重大意义。

目前，针对单变量的预测常用回归［1，2］与时间序列法［3-5］。吴泽宁等［6］采用回归分析法结合区间估计理论，改善了需水预测结果的偏差问题。VONK 等［7］建立基于气象参数和休假情况的支持向量回归模型进行日需水量的预测。李析男等［8］构建居民生活需水定额的时间序列模型，在交叉验证中都具有较高的Nash 效率系数。潘扎荣等［9］利用时间序列法及聚类分析等对河道内生态需水进行时空特征解析。DE 等［10］对比回归及时间序列等方法，指出在水需求预测方面仍有改进的余地。

通过大量实验发现回归模型并不能有效学习到水厂供水的周期性、趋势性及波动性，在预测时很难将过去的规律进行延伸，且容易生成伪回归方程［11，12］，从而导致预测失真。时间序列模型虽然可以学习到过去的规律，但是由于序列的非平稳特性在进行长期预测时，预测值以线性填充或者以平均值填充的概率较大。此外，目前需水预测中没有分类别建模是预测误差较大的主要原因。而城市不同行政区不同水厂的用水情况差别较大，统一建模不能真实反应各个水厂及行政区的用水特点，对于长时间序列的数据建模，会损失较远期与近期序列潜在的数量与特征关系。

因此，针对深圳市各水厂及行政区供水的周期性及波动性特点，考虑时间变化因子，提出KMeans 聚类算法［13，14］与季节性滑动平均自回归（seasonal moving average autoregressive，SMAAR）模型耦合方法，对47个水厂和10个行政区的供用水数据进行分类建模预测。根据序列特性通过滑动平均解决序列非平稳问题，使规律复杂的时间序列转化为规律简单的时间序列，并随着窗口的滑动进行预测。本文数据来源于深圳市数字水务系统和深圳市统计局。

1 分析

1.1 用水规律

深圳市的用水构成分为生活、工业、服务业、农业、建筑业及生态环境用水。由于深圳是全部城镇化功能完备的现代化超大型城市，因此农业及建筑业用水量很小且年际变化不大，两者年用水总量的和约占全市用水总量的7%。深圳一直在建设海绵城市，加上雨水利用工程的建设与污水回用量提高，因此生态用水增长不大，用水量约占年供水总量的6%。深圳用水占比较大的依次是生活用水、服务业用水及工业用水。生活用水一直处于深圳用水构成的第一大部分；服务业用水保持低速增长，2015年升至用水构成的第二大部分；随着工业产业结构不断优化调整及节水技术的不断应用，用水效率得到提升，工业用水总量从2011年的6.07 亿m3下降至2018年的4.85 亿m3，用水构成也从第二大部分下降至第三大部分。

通过对深圳市各区水务局、水源管理单位、水库管理处及水厂等地进行调研，对水厂供水的近五年实时数据分析发现，深圳目前用水结构基本稳定，整体趋势是：每年春节到元宵节期间全市流动人口全部返乡，是全年用水量最低的时期，日均用水量约为平时的56%。全年夏季用水多，冬季用水少，日用水量最大值多数情况出现在温度最高的7月份。全市总用水量逐年上升，农业、工业、建筑业及生态环境用水虽有波动但基本稳定，生活用水及服务业用水量逐年增加。

在经济及政策环境的吸引下，外来流动人口进入深圳，在为深圳带来充足劳动力的同时，也扩大了深圳市的用水人口基数，其后果直接体现在深圳市年用水总量不断上升。在2004-2018年间，全市用水总量增加了4.32 亿m3，增加的用水量主要表现在生活用水与服务业用水，可知增加的外来人口是深圳市用水总量增加的一大推力。

1.2 波动分析

2004-2015年深圳用水逐年增长较大，2008年经济危机及2012年三条红线指标确立导致用水量出现下降。2015-2019年，人口总量呈现明显的连续增长的态势，总人口年均增加约65 万，流动人口年均约增加30 万人，而用水总量增长幅度很小（图1）。通过分析发现，这是因为人口除了直接关系着用水总量的人口基数外，还通过改变用水结构影响着用水量。深圳各行政区的产业结构调查结果见表1。

图1 用水与人口变化Fig.1 Water use and population changes

由表1 可以看出，原特区（福田、罗湖、盐田及南山）的产业结构是以第三产业为主，4 个行政区第三产业比重分别为88.4%、90.77%、83.16%、83.03%，第三产业用水的特点就是波动性强。而宝安区、龙华区、坪山区及光明区是以第二产业为主，其次是第三产业，其中坪山区和光明区的第二产业比重分别达到75%和84.12%。大鹏新区隶属于龙岗区，因此龙岗区和大鹏新区的产业结构类似，第二产业和第三产业的比重相当。本文分别选择第三产业业和第二产业占比最大的罗湖区与光明区2019年逐日供水数据进行对比，见图2。

表1 2019年深圳行政区产业结构个Tab.1 Industrial structure of Shenzhen district in 2019

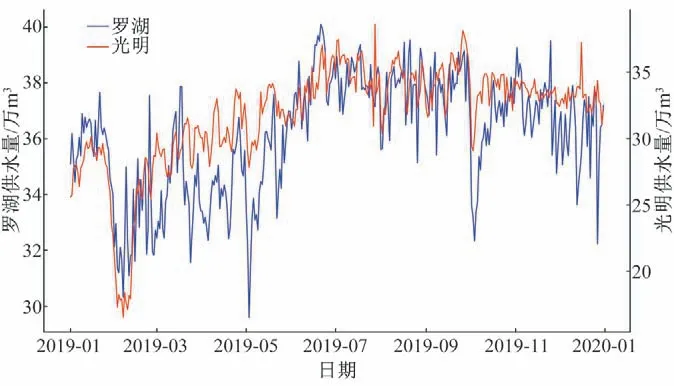
图2 罗湖与光明区2019年逐日供水序列Fig.2 The daily water supply sequence of Luohu and Guangming districts in 2019

由图2 可以看出，罗湖区与光明区的逐日供水规律为春假假期最低7月份最高，符合深圳市的总体用水规律。但是不考虑季节性因素，光明区逐日供水基本稳定波动较小，说明第二产业用水比较稳定；而罗湖区逐日供水波动较大，说明第三产业用水变化较大，且五一国庆供水有明显的下降，其他行政区也存在类似现象。说明第三产业是深圳各区用水波动大的主要原因，遇到假期居民外出旅游用水量下降，非假期期间人口倾向流动于以第三产业为主的行政区。考虑到逐日数据波动较大，不利于发现深圳各区的用水规律。因此，将2015年1月-2020年8月各区逐月供水的聚4类结果进行对比（图3），因为各区人口数量不一致，为了画图方便，将数据使用公式1进行归一化。为了保留数据真实的潜在特征联系，建模预测过程中不进行归一化。

图2 中罗湖区逐日供水序列波动较大，但是由图3（a）可以看出，逐月供水数据规律性明显，用水量在春节期间降到最低，春节后用水量开始回升，7月份用水量最大。图3（a）中5 个区的用水属于平稳型，年际间具有明显周期性规律，且年内变化规律基本一致。图3（b）可以看出，龙华区与光明区用水具有周期性且附带长期的增趋势，每年的用水总量有较明显增长，属于增长型。图3（c）和（d）属于波动型，即年内无明显规律，年际间周期性规律不显著，图3（c）属于先增后降的趋势，图3（d）属于先降后增的趋势。同时，分别选择罗湖区与光明区产能最大的两个水厂的逐日供水情况进行对比（图4）。

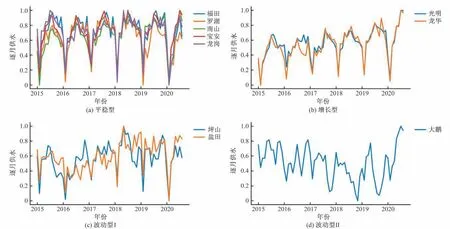
图3 行政区聚类结果Fig.3 Clustering results of the districts

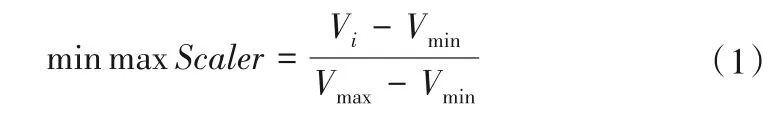
式中：Vmin与Vmax是时间序列最小值和最大值；Vi是序列的第i个值。

由图4 可以看出，东湖水厂2019年逐日供水情况与罗湖区的基本一致，日供水波动较为剧烈；甲子塘水厂的2019年逐日供水情况与光明区的规律基本一致，日供水保持平稳。水厂的逐日供水数据也具有和所在行政区一样的规律性。基于与行政区同样的考虑，将2015年1月-2020年8月水厂逐月供水的聚4 类结果进行展示（图5），也将数据归一化。考虑水厂较多，为了画图方便没有将全部水厂数据进行展示。

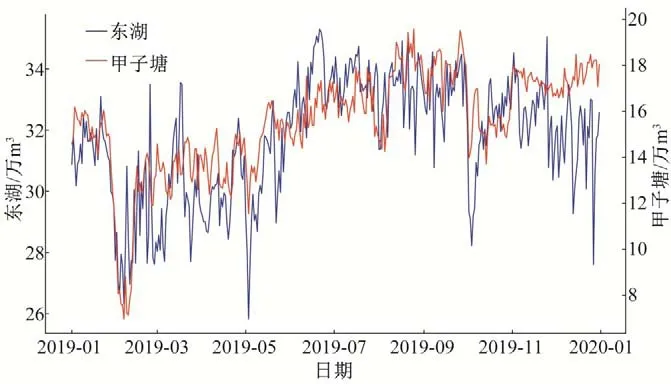
图4 东湖及甲子塘水厂2019年逐日供水序列Fig.4 The daily water supply sequence of Donghu and Jiazitang waterworks in 2019

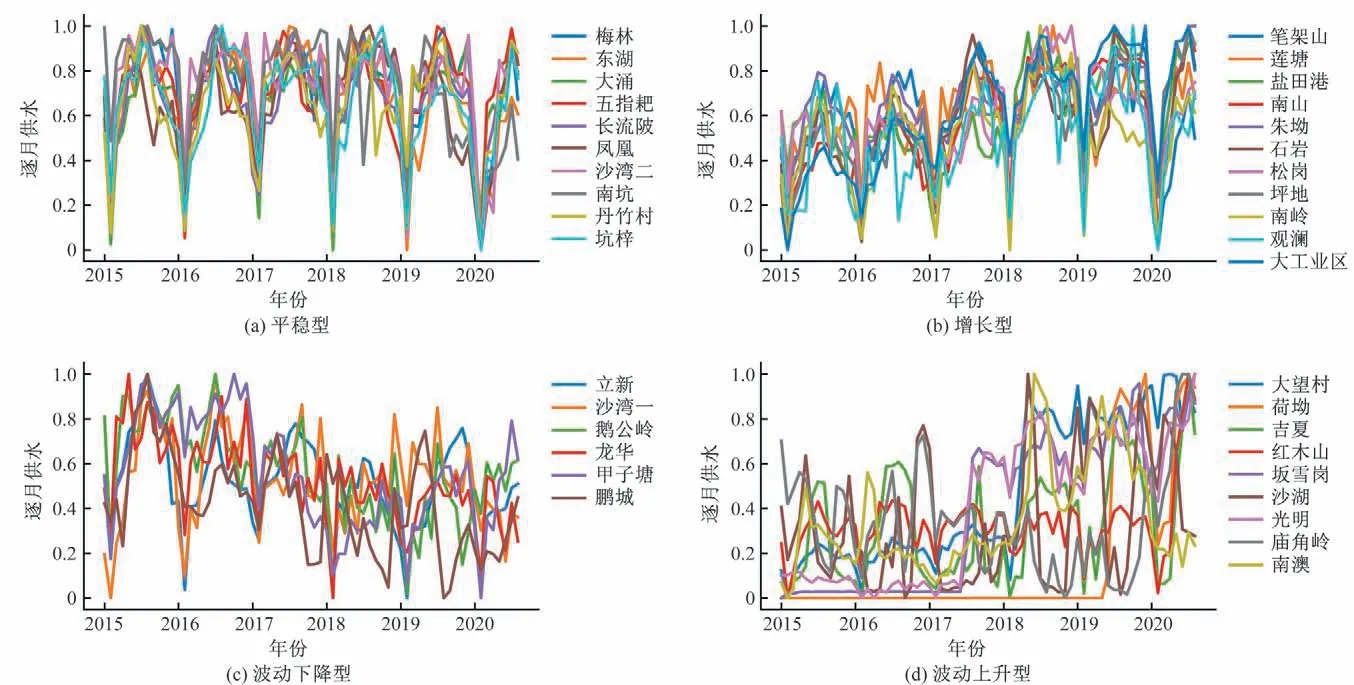
图5 水厂聚类结果Fig.5 Clustering results of the waterworks

2 SMAAR模型构建

水厂及行政区的逐日数据波动剧烈，而逐月数据存在较强的规律性与周期性，因此使用月数据建模。本文根据行政区及水厂月数据的不同聚类结果分别建模，保证模型能够充分学习每个类别的规律，更好地预测未来。考虑到长期趋势的影响，对数据进行滑动平均，对于周期性的规律，则以周期为滑动阶数进行滑动平均，对于周期性不明显的数据设置滑动阶数候选集合，通过训练模型选出最佳阶数。利用数据滑动平均抵消长期趋势的影响，对滑动平均后的数据序列建立自回归模型，并将预测结果与自回归滑动平均（autoregressive moving average，ARMA）模型［15，16］的预测结果进行对比。ARMA 模型虽然也进行滑动平均，但是该滑动关注的是残差项或者噪声，而本文的SMAAR是将原始序列进行滑动平均后进行建模。

水厂及行政区的原始数据序列虽然具有规律性，但是过程线仍然存在较大变化，这种变化对于建模存在较大干扰。通过对原始序列进行滑动平均，屏蔽掉这种复杂的变化，使复杂的数据序列变成波动较小规律简单的新序列。图6 和图7 分别是行政区与水厂的4 个类别的滑动平均后生成的新时间序列，滑动公式如下。

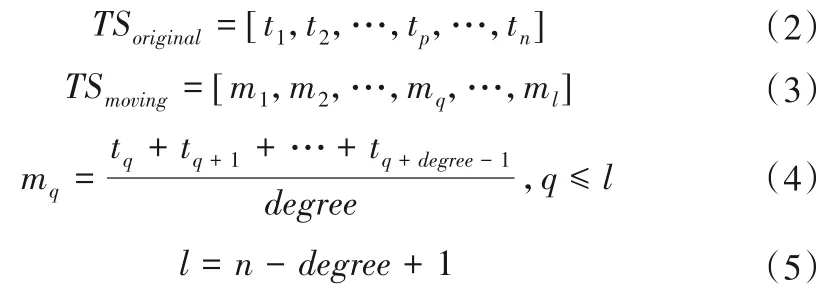
式中：n是原序列长度；l是新序列长度；degree是滑动阶数。

由图6和图7可以看出，4个类别生成的新序列波动小且规律简单，使用这样的序列建模将更高效，模型的泛化能力也将更强，预测结果只需要逆向滑动即可还原。

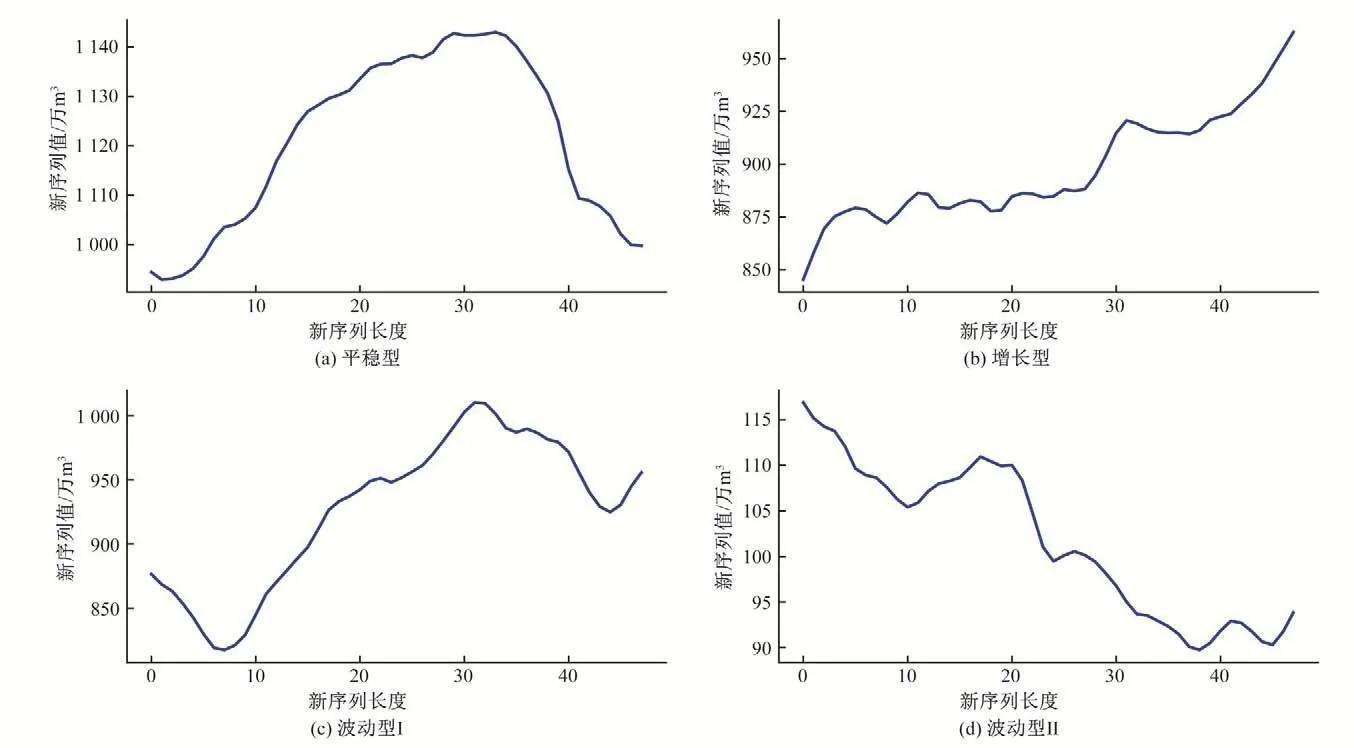
图6 行政区4个类别新的时间序列Fig.6 The new time series of the four categories of districts

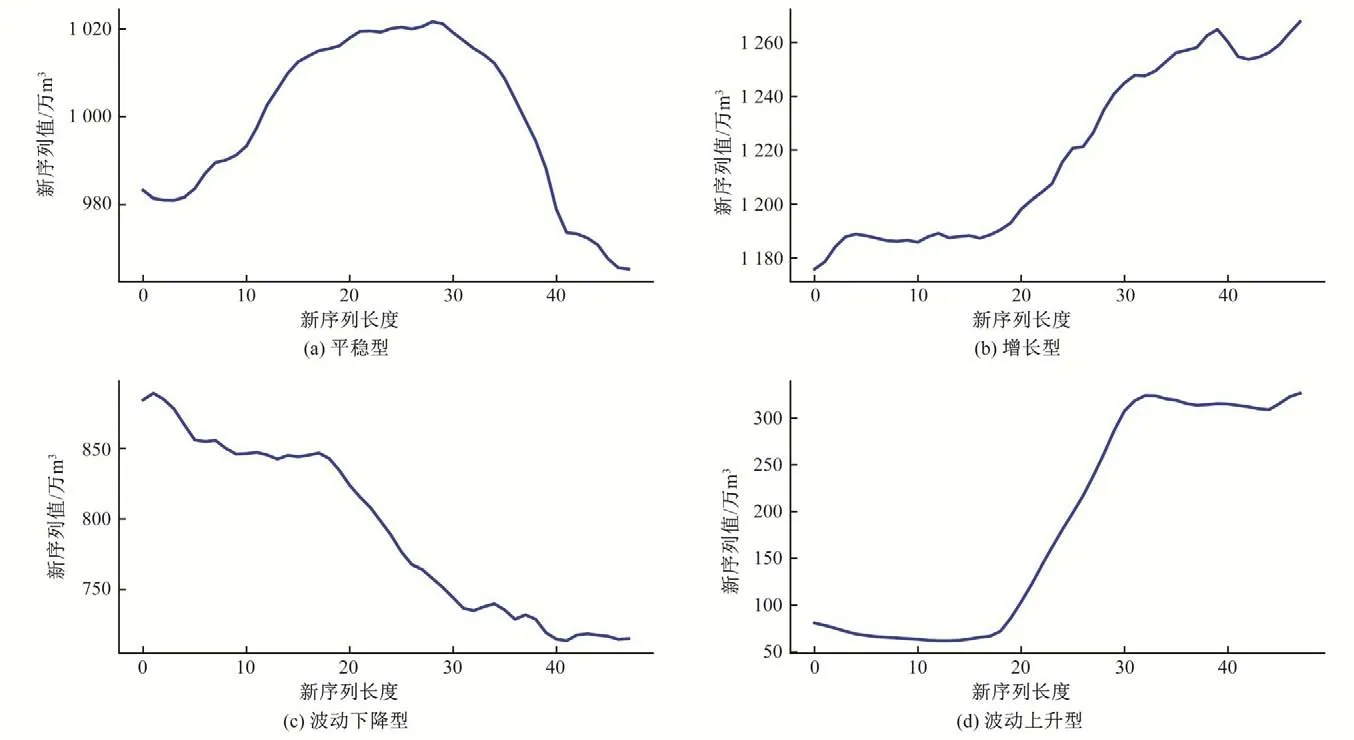
图7 水厂4个类别新的时间序列Fig.7 The new time series of the four categories of waterworks

3 结果

本文从10个行政区的4个聚类结果中分别选4个区的数据进行对比分析（表2）。其中平稳型、增长型、波动型I 及波动型II分别选择罗湖、光明、坪山及大鹏区。选择罗湖区和光明区是因为他们分别是第三产业和第二产业占比最大的行政区，而坪山区是从波动型I的两个区中随机选择的。通过对比逐月的模型估计值与实际值相对误差（relative error，RE）来判断模型的性能。

式中：e是模型的估计值；y是实际值。

由表2 可以看出，行政区的预测结果，SMAAR 的RE小于ARMA。以光明区为例，2020年1月-8月SMAAR模型预测结果的RE比ARMA 模型分别提高17.39%、42.11%、27.27%、33.33%、62.50%、66.67%、60.87%、77.78%。表2 中大鹏区的RE较大，是因为大鹏区用水规律波动性大导致模型预测结果的RE增大。类似地，同样选择4 个水厂的结果进行对比（表3），他们是分别位于不同行政区且产能较大的东湖水厂、朱坳水厂、龙华水厂及光明水厂。

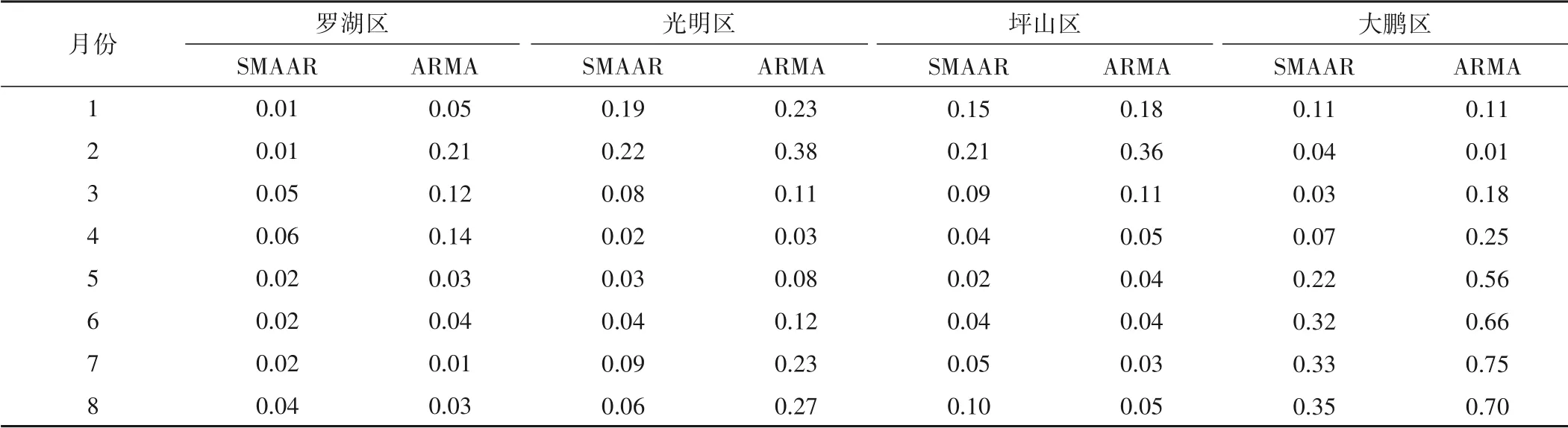
表2 2020年行政区预测结果的RE对比Tab.2 RE comparison of the forecast results of districts

由表3 可以看出，水厂的预测结果，SMAAR 的RE小于ARMA。以朱坳水厂为例，2020年1-8月SMAAR 模型预测结果的RE比ARMA模型分别提高了50%、67.35%、25%、37.5%、0%、100%、90%、92.31%。由此可见，SMAAR 模型表现出了较强的泛化能力。

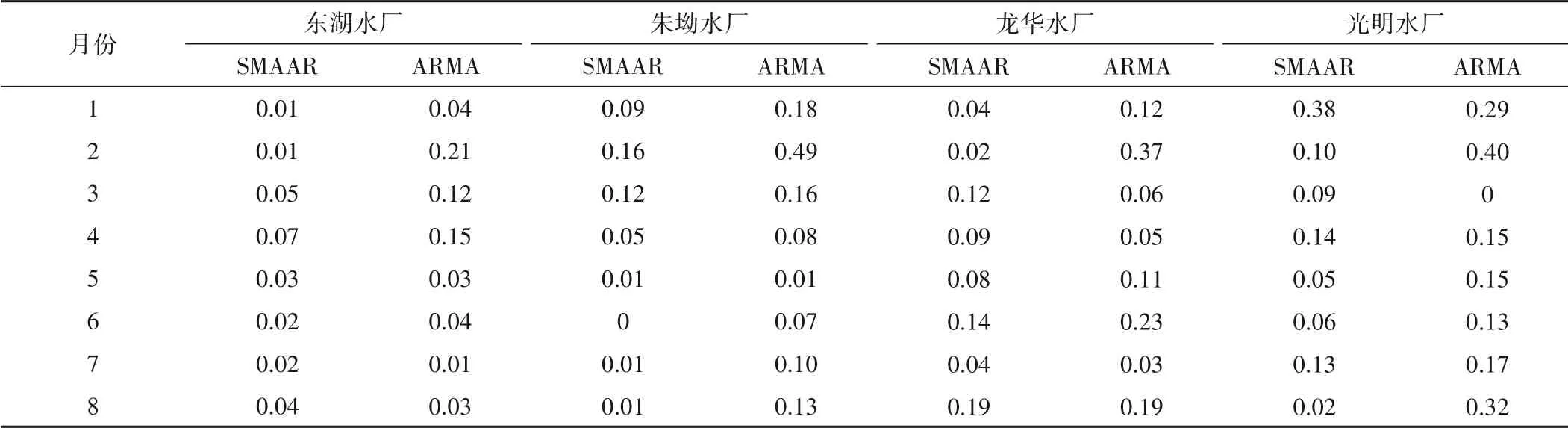
表3 2020年水厂预测结果的RE对比Tab.3 RE comparison of forecast results of waterworks

将47 个水厂及10 个行政区的分类预测结果进行求和汇总得到深圳的月用水数据（表4），并与SMAAR 直接使用深圳月滑动数据预测的结果及ARMA的结果进行对比。

总体而言，通过水厂与行政区汇总得到的需水数据的RE最小，可知分类建模可以更加准确地预测全市的需水情况。此外，由表4中可以看出，水厂汇总的RE比行政区汇总的RE还要小，使用月滑动数据的RE要比行政区汇总的RE大，可知越细化建模，预测结果越贴近真实数据，证明此种建模方法是有效的。ARMA 的RE最大说明ARMA 模型的误差最大。城市需水预测结果误差较大，主要原因就是没有进行分类建模。本文细化到一类数据建一个模型，将结果进行汇总，这样的精细化预测可以有效解决结果误差较大的现象。

表4 2020年深圳用水预测的RE对比Tab.4 RE comparison for water use forecast in Shenzhen

同时，通过实验还发现，模型在进行逐日长期预测时性能往往会变差，预测结果很可能全部是平均值或者中位数。因此，本文将模型对逐日数据进行建模预测，对比2种模型的泛化能力（图8）。

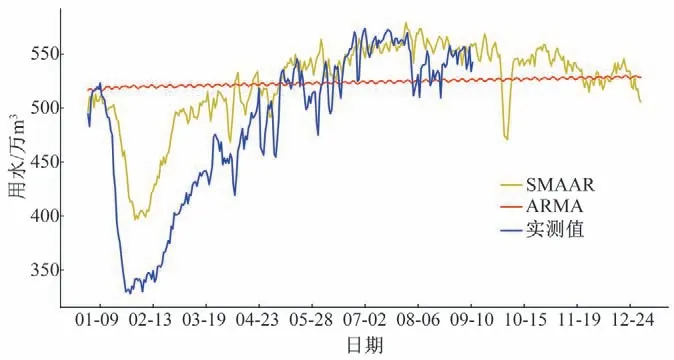
图8 逐日预测结果对比（2020年）Fig.8 Comparison of daily forecast results

由图8可以直观看出，在2020年1-8月共254 d逐日预测结果中，ARMA 的性能恶化，预测结果全部在平均值附近波动，无法有效预测需水。而SMAAR 依旧表现出了良好的性能，254 d的预测数据与实际统计数据的规律基本一致，且误差较小（见图9），春假及五一假期的用水下降规律也预测成功。根据历史规律，深圳国庆假期用水会出现一定幅度的下降，国庆之后全市用水量缓慢下降，由图8 可以直观地看出，2020年9月-12年SMAAR的预测结果完全符合实际。

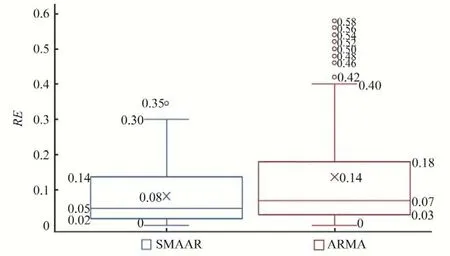
图9 RE箱图对比Fig.9 RE box plot comparison

由RE箱图可以直观看出，SMAAR 预测RE的平均值是0.08，中位数是0.05，预测误差较小。箱图的四分位值分别是0、0.02、0.14、0.3，说明模型稳定性强且254 d 逐日预测结果较精确。此外，SMAAR 模型的离群点只有一个，说明SMAAR 模型可靠性强，预测值曲线与实际值曲线拟合较好，只有一个点偏离较远。而ARMA 模型预测结果全是平均值，即实际值曲线波动大误差就大，曲线波动小则误差小，不具有现实意义。

二三产业及外来人口的快速增长，将导致深圳用水量的快速增长。如果能够准确地预测深圳市未来一年的需水情况，就可以制定较为精确的年度引水计划，可以有效地对未来的用水情况进行全局把握，能够针对性地进行水库蓄水工作，从而保障深圳的供水安全。