未知纬度条件下基于空间圆拟合的SINS初始对准方法
2021-09-28管世印张志利周召发
管世印,张志利,周召发,梁 哲
(火箭军工程大学导弹工程学院,西安 710025)
0 引言
捷联惯导系统(Strapdown Inertial Navigation System,SINS)在进入导航状态前必须进行初始对准。SINS的初始对准通常需要精确的纬度值来构建参考矢量模型,而当对准环境较为恶劣时,如在隧道、水下、地下等环境中获得精确的纬度值并不容易,研究未知纬度条件的对准具有一定的理论意义与应用背景。为此可以从两方面考虑,一是进行纬度的估计,通过2个不同时刻的重力加速度夹角与纬度之间的几何关系进行求解[1-2];二是通过重力矢量几何运算求得北向信息,改进对准算法[3-4]。
在处理晃动基座对准问题上,通常采用基于惯性系或中间参考坐标系的对准方法,通过空间中凝固某一时刻坐标系作为过渡传递矩阵,求得对准矩阵,且粗对准的结果尤其是偏航角的对准结果往往误差较大[5-7]。
理想情况下,在任一惯性系中观察,重力矢量绕地轴旋转形成一锥面,重力矢量的端点形成一空间圆即圆锥底面。为此,本文以初始时刻凝固载体坐标系为惯性系,对重力矢量低通滤波后进行空间圆数值拟合得到旋转地轴矢量,通过矢量解算得到对应时刻的地理坐标系,进行矩阵连乘得到对准矩阵,完成对准过程。
1 基于空间圆拟合的对准方法
定义地理系东北天为导航坐标系n系,载体坐标系为b系,初始时刻载体坐标系为b0系,初始时刻地理坐标系为n0系。
1.1 传统的基于惯性系的对准方法
基座晃动会引入晃动角速度,而地球自转角速度ωie数量级为10-5rad/s,导致陀螺仪无法从测量值中将地球自转角速度识别出来,因此基于地球自转角速度和重力加速度矢量的双矢量定姿方法无法在晃动基座下使用[8]。为此,传统晃动基座对准方法采用基于重力矢量的惯性系间接对准方法,根据惯性系的不同,可以分为地理系、地心惯性系、地球系等,以地理系为例,其对准传递矩阵为
(1)
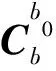
(2)
式中,sl、cl为lat的正弦和余弦值。
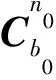
(3)
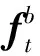
多矢量Wahba方法是指通过构建指标函数求解最优矩阵,通常其求解方法包括奇异值分解法和最优四元数估计方法等[10-12],不同的求解方法之间存在等价性[13]。对重力矢量进行m次观测时的指标函数为
(4)
式中,ωi为标量权值,可选为1。
1.2 基于空间圆拟合的对准模型
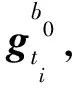
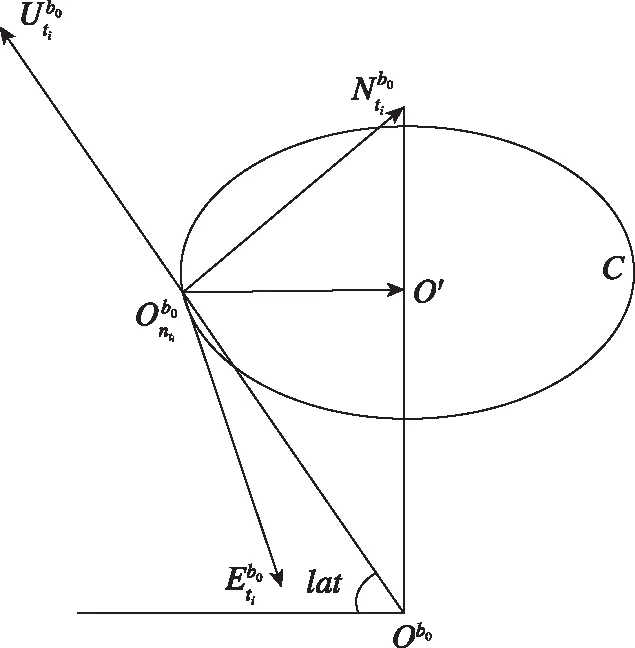
图1 凝固载体系内构建地理坐标系示意图
(5)
(6)
(7)
通过矩阵连乘
(8)
2 旋转地轴解算模型
2.1 重力矢量投影至载体系
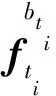
(9)
式中
(10)
由于基座的晃动往往会引入线运动的干扰,导致无法使用真实的重力信息,为此通常选择引入低通滤波器等方式对投影的重力矢量进行滤波处理。滤波原理为在b0系内观察重力信息,重力信息的变化频率为
(11)
而一般情况下基座晃动引起的线运动干扰的频率远高于此,因此可以采取低通滤波处理线运动的干扰。
低通滤波器参数通常设置为:滤波器类型为巴特沃斯低通模拟滤波器,通带频率Wp=0.001Hz,通带衰减Rp=1dB,截止频率Ws=0.05Hz,阻带衰减Rs=40dB,采样频率为125Hz,该滤波器可以使低频的重力信号通过而对高频的扰动信号起到衰减作用。
2.2 求解拟合端点平面方程
ax+by+cz-1=0
(12)
式中,a、b、c为平面参数,理想情况下,b0系内所有重力矢量投影点端点均在一个平面方程上,以此构建误差观测方程
(13)
根据最小二乘理论,平面法向量为
[a,b,c]T=(ATA)-1ATI
(14)
式中
(15)
(16)
2.3 求解拟合圆圆心坐标
根据圆心O′(x0,y0,z0)与任意弦中点连线垂直于弦的特点,对于圆上任意两点可构建中垂线方程
(17)
结合平面方程(12),可构建误差观测方程
(18)
式中
(19)
式(18)和式(19)即为间接平差模型[14-15],根据最小二乘理论,圆心O′的最小二乘解为
O′T=(FTPF)-1FTPl
(20)
其中,权值矩阵P为单位阵
(21)
(22)
通过上述分析可知,对准方法不需要知道具体的位置信息,对准前首先利用惯性器件测量信息进行空间圆拟合,得到空间圆圆心O′,再通过空间矢量计算与矩阵连乘得到对准矩阵。
3 仿真验证
为说明基于空间圆拟合SINS初始对准方法(以下简称为拟合对准方法)的有效性,设置仿真环境如下:
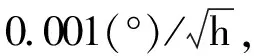
(23)
由于基座晃动引起的载体3个轴向的线运动干扰(单位为m/s)设定为
(24)
分别使用拟合对准方法、积分双矢量方法和多矢量Wahba方法进行50次对准,其中多矢量Wahba方法采用最优四元数估计方法进行求解,其姿态角误差如图2所示,姿态角误差均值如表1所示。
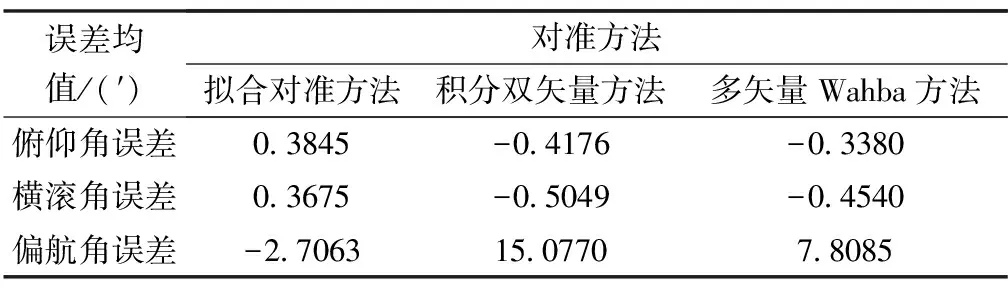
表1 三种对准方法姿态角误差均值比较
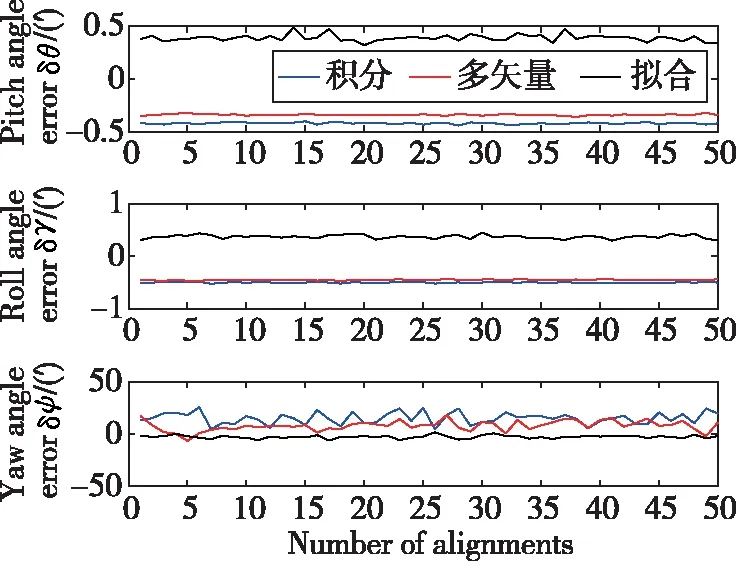
图2 不同对准方法姿态角误差
通过分析可知,三种方法的姿态角误差均值均能达到粗对准要求,且三种方法的水平姿态角精度相当,拟合对准方法的偏航角精度相比于积分双矢量方法和多矢量Wahba方法分别提升了12.37′和5.10′。
从算法稳定性上看,如表2所示,多矢量Wahba方法的水平姿态角误差稳定性要好于拟合对准方法和积分双矢量方法,但偏航角误差稳定性不如拟合对准方法。

表2 三种对准方法姿态角误差均方差比较
需要说明的是,与积分双矢量方法和多矢量Wahba方法不同的是,为了取得较好的空间圆拟合效果,拟合对准方法需要利用一定时间段内的惯导测量数据进行拟合来得到对准结果,在多次验证中表明,最小拟合时间可预先设定为1min,这也是下一步需要对算法进行优化的方面。
4 结论
1)本文提出了一种未知纬度条件下基于空间圆拟合的SINS初始对准方法,首先将重力信息投影至凝固载体系并进行滤波处理,根据重力矢量绕地轴旋转特性建立间接平差模型,利用惯组测量数据进行空间圆拟合得到旋转地轴,并通过几何关系解算对准矩阵;
2)为了获得较好的空间圆拟合效果,通常需要采集一定的惯导测量数据才能进入对准过程,实时性不如传统方法,但仍可在常用对准时间内获得优于传统方法的对准精度,下一步研究的侧重点在于对算法实时性进行优化;
3)与传统对准方法相比,其优点在于通过矢量积反求对准点纬度,对准不需要精确纬度信息且偏航角对准精度与稳定性提升明显。
