多系统混频非差非组合精密单点定位方法研究
2021-09-28李宏宇侯毅男杨福鑫
赵 琳,李宏宇,侯毅男,杨福鑫,李 亮
(哈尔滨工程大学智能科学与工程学院,哈尔滨 150001)
0 引言
精密单点定位(Precision Point Positioning,PPP)具有作业灵活、无需基站辅助的优势,广泛应用于海洋高精度定位,具有重要的应用价值。根据电离层处理策略的不同,PPP模型可以分为无电离层组合模型、Uofc模型以及非差非组合模型。其中,非差非组合PPP模型直接使用原始伪距和载波相位观测值,具有不会放大噪声;可引入外部电离层约束,加快收敛;可提供高精度的电离层延迟信息的优点[1]。随着全球导航卫星系统(Global Navigation Satellite System,GNSS)的建设与发展,围绕多系统多频率特征开展的相关研究已成为GNSS应用领域的重要研究内容。卢秋阳结合实测北斗三频数据,通过对现有三频周跳检测与修复方法进行系统的比较研究,提出了一种基于电离层变化的实时周跳探测方法[2]。王泽民等论述了Galileo系统4个频率的载波组合观测值及相关的误差特性,并按一定标准筛选出具有特定性能的组合观测值[3]。张小红等从定位精度和收敛性两方面,研究分析了三频无电离层组合模型、三频消电离层组合模型和三频非组合模型PPP静态及动态定位性能,并与传统双频无电离层组合进行比较,结论是三频PPP定位精度有所提高,并且具有更高的可靠性和抗差性能[4]。M.Elsobeiey根据不同策略选取了9组全球定位系统(Global Positioning System,GPS)三频线性组合PPP方案,实验结果表明,三频线性组合PPP可将传统双频PPP的收敛时间和定位精度提高大约10%[5]。李博峰等研究了使用GNSS组合观测量进行长距离实时精密导航的方法[6]。X.Lou等研究了GPS+GLONASS+BDS+Galileo四系统联合的非差非组合PPP模型与算法,并利用105个多模GNSS实验跟踪网(Multi-GNSS Experiment,MGEX)测站的多系统观测数据,分析了不同系统联合的单、双频PPP定位精度和收敛速度,结果表明,多系统观测值的加入可以明显改善PPP定位性能和可靠性[7]。
在多模多频条件下,沿用现有组合观测值的策略(无电离层组合)处理数量众多的原始观测值,将存在以下问题:1)随着信号个数的增加,待求的独立偏差个数增多,特征组合数量增加,合理选择与评价最优组合的难度就会随之增加;2)特征组合会损失某类信息;3)需要所有观测单元的原始观测值中必须包括组合所需的特征信号,若缺失其中一类观测值,将使得其他观测值也无法参与解算,从而导致原始观测信息损耗;4)需要针对不同的解算目的选择特定的观测组合。采用非差非组合思路能够最大限度地保留原始观测信息,利于单频、双频、多频模型的统一表达,灵活兼容各类应用需求。
现有关于多模多频的研究几乎没有将多模与多频结合起来,研究多系统采用多系统双频模型,研究多频率采用单系统三频模型。这主要是由于除了北斗系统外,其余系统无法保证全星座都提供三频信号。
综上,本文对多系统混频非差非组合PPP进行了研究,推导了多系统混频模型即北斗三频+GPS双频+GLONASS双频PPP模型,实现了多系统混频非差非组合PPP,进而达到增强PPP可靠性、提高PPP定位性能的目的。
1 多系统混频非差非组合PPP函数模型
随着多导航系统多频观测值的获取以及数据处理理论的深入发展,相对硬件延迟的定义也进一步延伸,通常分为系统间偏差(Inter-System Bias,ISB)和频间偏差(Inter-Frequency Bias,IFB)。ISB描述了不同系统间的通道延迟偏差,在使用多模信号时,必须要考虑该项偏差;IFB为同一系统不同频率信号的通道延迟偏差,由于GLONASS系统采用频分多址(Frequency Division Multiple Access,FDMA)技术,不同卫星具有不同的频率、伪距和载波IFB,需考虑该项偏差。北斗系统采用三频信号,同样需考虑IFB。
1.1 标准双频非差非组合PPP模型
本文模型采用北斗三频+GPS双频+GLONASS双频非差非组合PPP模型,需顾及系统间偏差、GLONASS频间偏差以及BDS频间偏差。为了方便推导后续顾及IFB、ISB的PPP模型,首先推导统一的标准双频非差非组合PPP模型。
非差非组合PPP处理模型由原始伪距和载波相位模型推导而成,由于引入了各信号特征性时延偏差和电离层估计等参数,在灵活建模的同时,带来许多参数间相关的问题。卫星端非校正伪距硬件延迟(Uncalibrated Code Delay,UCD)与卫星钟差线性相关;接收机端UCD与接收机钟差及电离层参数线性相关;非校正相位硬件延迟(Uncalibrated Phase Delay,UPD)与模糊度线性相关。在没有额外基准约束的情况下,上述参数无法分离,故无法直接求解。
通常的解决方式是通过参数规整,利用钟差、电离层延迟和模糊度等参数分别吸收部分伪距硬件延迟。相位硬件延迟与模糊度具有强相关性,且通常具有极高的时间稳定性,可被模糊度完全吸收[8]。
此外,观测方程中的其他误差项如卫星和接收机天线相位中心改正、测站对流层天顶干延迟、相对论效应、潮汐负荷形变(固体潮、极潮和海潮)、萨奈克效应和卫星天线相位缠绕等改正,均需事先通过模型改正[9]。
为了更好地描述参数规整,定义如下表达式
(1)

IGS精密卫星产品一般基于P1/P2无电离层组合观测值估计,因此,其提供的卫星钟差产品包含了双频P1/P2伪距观测值UCD的线性组合,即


(2)

(3)

引入精密卫星轨道和钟差改正,对原始观测方程进行参数规整,线性化后可以得到标准双频非差非组合PPP模型,具体方程如下
(4)
(5)
(6)
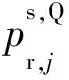
该模型对应的待估参数X为
(7)
1.2 GLONASS非差非组合PPP模型
GLONASS采用频分多址技术,需要考虑伪距频间偏差的影响。在本文中考虑将频间偏差模型化为频率数的二次多项式函数。
GLONASS伪距频间偏差可以表示为

(8)

(9)
该模型对应的参数向量X可表示为
(10)
后续模型中,GLONASS中的伪距频间偏差都采用该处理策略。
1.3 北斗三频非差非组合PPP模型
根据式(4)和式(5)可以得到北斗三频非差非组合模型,但在第三个频率上的伪距观测值的码间偏差(DCBr,13)无法被电离层参数完全吸收。所以需要在第三个频率的伪距上引入一个额外的频间偏差参数IFB,即
(11)
其中

(12)
IFB是B3频率上的伪距频间偏差,作为时间常数估计。
该模型的待估参数X为
(13)
1.4 多系统混频非差非组合PPP模型
将式(4)和式(5)扩展到多系统环境下,考虑IFB参数;引入ISB参数,以GPS接收机钟差作为参考,可得到多系统混频PPP模型,即
(14)
(15)
该模型对应的参数向量X可表示为
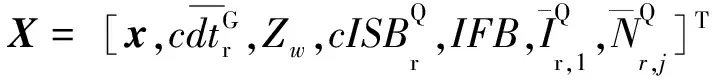
(16)
2 试验及结果分析
本文采用开源软件GAMP进行二次开发,并在其中扩展了多系统混频PPP处理模块[10]。
本节选取了JFNG、CUT0、NNOR、SIN1这4个站点在2018年5月(年积日为121~124)总计4d的30s采样间隔的观测数据进行实验分析。实验采用了德国地学研究中心提供的精密轨道和钟差产品,卫星和接收机天线相位中心改正采用IGS绝对天线相位中心改正模型igs14.atx。由于BDS接收机端的天线相位中心改正不可用,因此用相应的GPS信号对应的接收机端天线相位中心改正替代。卫星截止高度角设置为10°。具体的PPP处理策略如表1所示。

表1 多系统混频PPP处理策略
2.1 静态定位结果分析
由于双频非差非组合模型相比无电离层组合模型更有优势,本节使用两种模型进行静态精密单点定位,一种是GPS+GLONASS+BDS双频非差非组合模型(简称为GRC-2),另一种为北斗三频+GPS双频+GLONASS双频模型(简称为GRC-3)。图1给出了4个测站两种PPP定位模型下连续4d单天静态定位精度均方根(Root Mean Square,RMS)的平均值。图1中,横坐标轴表示4个测站,纵坐标表示E、N、U方向平均RMS。从图1中可以看出,两种PPP模型在各测站的定位精度在E、N、U方向均优于4cm,GRC-3模型的定位精度优于GRC-2模型。具体分析可知,在JFNG与NNOR站点下两种模型的定位精度几乎没有差距,这2个站点下的定位精度相较其余2个站点(CUT0、SIN1)更好,NNOR站点的E、N方向的定位精度达到了毫米级;CUT0、SIN1站点的定位精度稍差,SIN1站点GRC-2模型下E向的定位精度较差,达到了4cm,这种情况下,GRC-3模型下E向的定位精度有所提升。

图1 两种PPP模型4个测站单天静态定位平均RMS
表2统计了两种PPP模型下4个测站连续4d单天静态解的平均值。从表2的统计结果来看,相较于多系统双频非差非组合PPP模型,多系统混频非差非组合PPP模型的定位精度有所提高,以单个测站为例,NNOR站点下两种模型的定位精度在E、N方向达到毫米级,定位结果较好,GRC-3模型相较GRC-2模型的定位精度有所提升,但提升在5%以内,可以认为两者精度相当。可以说,当GRC-2模型能取得良好定位精度时,使用GRC-3模型也能取得同水平的定位精度,但很难提升。SIN1站点的情况不同,该站点在E、U方向的定位精度在4个测站中是最差的,GRC-3模型的定位精度相较GRC-2模型取得了较大提升,在东向上提高了12.5%,在天向上提升了21.3%。可以看出,当GRC-2模型的定位结果较差时,GRC-3模型的定位精度会有明显提高。从4个测站的RMS平均值综合来看,GRC-3模型的定位精度相较GRC-2模型有所提高,在东向上提高了9.6%,北向上相当,天向上提高了11%。
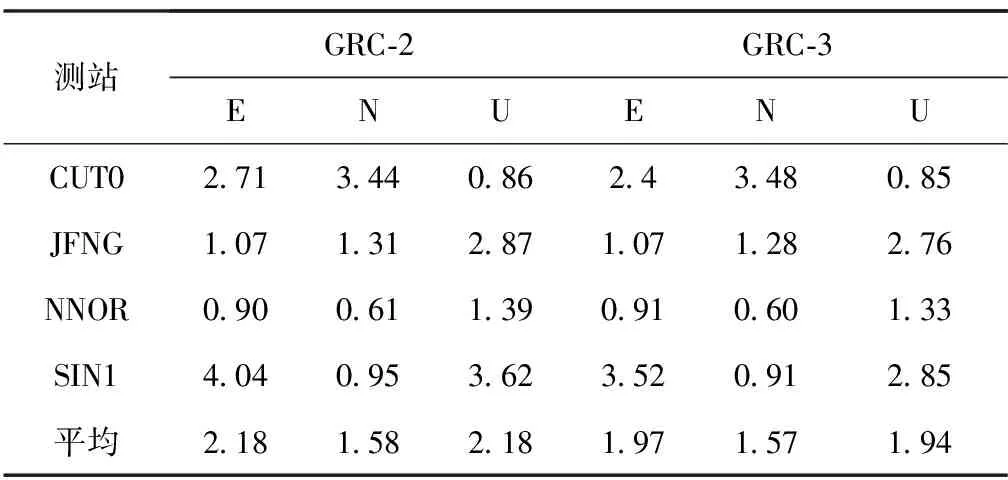
表2 两种模型4个测站单天静态定位RMS统计表
表3统计了4个测站的平均收敛时间,以E、N、U这3个方向定位偏差连续20个历元均优于10cm时定义收敛。从表3中可以看出,两种模型下4个测站的静态定位平均收敛时间在15min左右,GRC-3模型下的收敛时间较GRC-2模型有所增长,收敛性能有所下降。这主要是因为使用GRC-3模型有更多待估参数,虽然提高了冗余度,但在定位的初始阶段,待估参数更易受观测方程病态性的影响,影响了GRC-3模型的收敛时间,并且GRC-3模型的数据处理时间也更长。
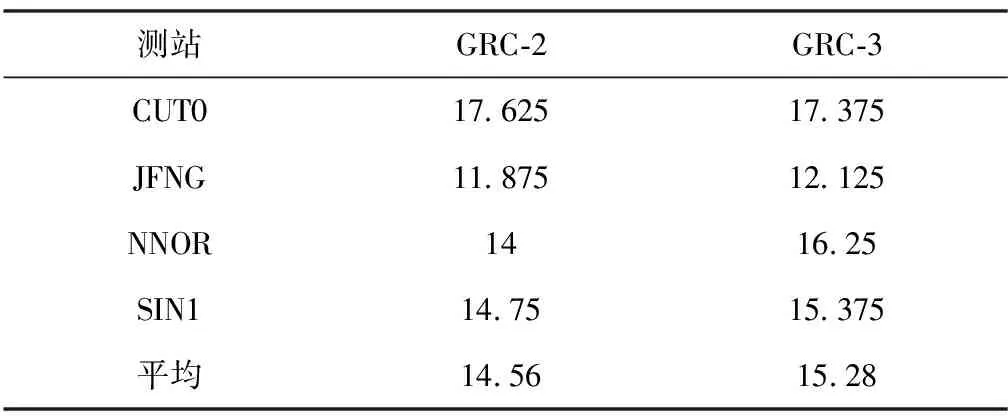
表3 两种模型4个测站静态定位收敛时间统计表
2.2 模拟动态定位结果分析
本节使用两种模型进行伪动态精密单点定位,即解算测站坐标时使用白噪声过程进行估计。图2给出了4个测站两种PPP定位模型下连续4d单天动态定位精度RMS的平均值。图2中,横坐标轴表示4个测站,纵坐标表示E、N、U方向平均RMS。从图2中可以看出,除了SIN1站点,两种PPP模型在各测站的定位精度在E、N、U方向均优于4cm,GRC-3模型定位精度优于GRC-2模型。在JFNG与NNOR站点下两种模型的定位精度几乎没有差距,这2个站点下的定位精度相较其余2个站点(CUT0、SIN1)更好。CUT0和SIN1站点的定位精度稍差,SIN1站点GRC-2模型下天向的定位精度较差,达到了7cm,这种情况下,GRC-3模型下天向的定位精度有所提升。
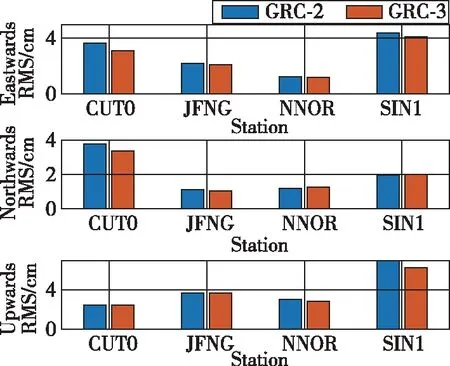
图2 两种PPP模型4个测站单天动态定位平均RMS
表4统计了两种PPP模型下4个测站连续4d单天伪动态解的平均值。从表4的统计结果来看,同静态结果类似,相较于多系统双频非差非组合PPP模型,多系统混频非差非组合PPP模型的定位精度有所提高,从4个测站的RMS平均值综合来看,在东向上提高了7.3%,北向上相当,天向上提高了5.7%。
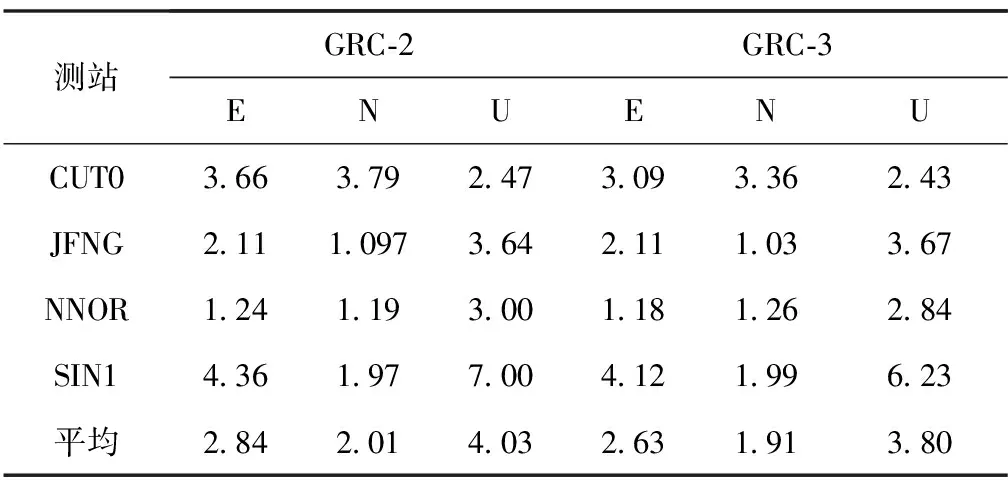
表4 两种模型4个测站单天动态定位RMS统计表
表5统计了4个测站的平均收敛时间,以E、N、U这3个方向定位偏差连续20个历元均优于10cm时定义收敛。从表5中可以看出,两种模型下4个测站动态定位的平均收敛时间在23min左右,与静态结果类似,GRC-3模型下的收敛时间相较GRC-2模型有所增长,收敛性能有所下降。

表5 两种模型4个测站动态定位收敛时间统计表
3 结论
本文基于测站的观测数据,主要从定位精度和收敛性方面,研究分析了多系统混频非差非组合模型PPP的静态及动态定位性能。
同多系统双频非差非组合PPP相比,多系统混频非差非组合PPP的定位精度有所提高,静态解RMS在东向提高了9.6%,北向相当,天向提高了11%;动态解RMS在东向提高了7.3%,北向相当,天向提高了5.7%,但多系统混频PPP的收敛时间并没有提升。
在多系统双频PPP因某一频率异常导致定位精度较差时,多系统混频PPP仍能保证较高的定位精度,由于本文实验选用的观测数据都从测站下载,质量较好。有理由可以相信,在使用质量稍差的观测数据,如动态车载实验的观测数据时,多系统混频PPP模型相较多系统双频PPP模型可以得到更好的提升。
综上,多系统混频PPP的定位性能有所提升,但收敛时间和解算速度还有待进一步研究。
