改进物品相似度计算的协同过滤算法

方 惠，李 民，邓秀辉，余开朝

（昆明理工大学机电工程学院，云南昆明 650500）

0 引言

在信息爆炸的时代，用户难以从大量数据信息中快速精确地获取所需信息，容易产生信息超载（Information Overload）问题［1］。为帮助用户快速找到感兴趣的产品，推荐系统应运而生。近年来，推荐系统在电影、新闻、电子商务等诸多领域中起到了重要作用，有效减轻了信息超载现象。作为推荐系统的核心部分，推荐算法成为人们研究的热门对象［2］。目前协同过滤（Collaborative Filtering，CF）算法已经应用于互联网的众多领域［3-6］，其实现原理是根据用户以往在网络中搜索产生的数据发掘其可能喜欢的东西，根据喜好内容不同将用户分成小组，推荐与其爱好相近的商品［7］。但该算法存在一些不足，如没有考虑到用户兴趣会随时间推移而发生变化，热门物品也可能会影响相似度计算。以上问题均会导致推荐系统的精确度出现偏差，从而使用户得不到满意的推荐结果。

CF 算法是目前使用最广泛、最有效的算法之一［8］，但存在推荐精确度不高等问题，许多学者对此进行了研究。董立岩等［9］在相似度矩阵的计算过程中融入时间衰减因子，使推荐结果更具时效性；尹毫等［10］提出在物品相似度计算中融入物品惩罚因子以修正物品相似度矩阵的计算，在推荐精确度方面显著提高；熊丽荣等［11］考虑到用户兴趣会随着时间发生变化，故采用时间效应模型函数处理用户历史评分数据，推荐效果明显优于传统算法；邓华平［12］提出在CF 算法中加入项目聚类和时间衰减函数，加快了最近邻居集合的寻找速度，提升了推荐精确度；崔国琪等［13］提出在物品相似度计算中融入物品惩罚因子，加入惩罚因子的CF 推荐算法在保持算法精确度的同时，可在一定程度上降低推荐结果流行度；Chen 等［14］从用户评分角度出发，将平衡因子引入传统的余弦相似度算法中，用于计算不同用户间的项目评级尺度差异，提出了一种改进的基于优化用户相似度的CF 算法，推荐精确度显著提高；Lee 等［15］提出将偏好模型的概念应用于CF 算法中，修正用户—物品评分举证，有效提高了该算法的精确度和召回率。

以上改进算法仅提高了商品推荐的精确度，但未考虑到用户兴趣会随时间推移而发生变化，亦未考虑将时间衰减函数与物品惩罚因子融合到一起。针对以上问题，本文在原有研究成果的基础上，在传统相似度矩阵计算中引入时间衰减函数和物品惩罚因子，得到改进相似度矩阵的推荐算法在精确度、召回率和F1 值上均比传统CF 推荐算法明显提高，更有利于推荐出使用户满意的结果。

1 理论基础

1.1 传统CF 算法

传统CF 算法可分为基于用户的推荐算法（User CF）和基于商品的推荐算法（Item CF）。User CF 算法的主要思想为寻找与目标用户兴趣相似的用户集合，同时将该集合中用户喜欢但没有听过的商品推荐给他们。Item CF 算法的主要思想为根据用户历史评分计算物品之间的相似度，通过物品相似度和用户历史行为预测用户以往喜欢商品的相似物品［16］。传统CF 算法的实现过程为：首先获取历史评分数据，构成网络用户—项目评分矩阵；然后计算网络用户或项目间的评分相似度，按照相似度对网络用户或项目进行排列，排列靠前的几个用户或项目可以被看作是邻居，利用得到的相似度和邻居用户历史评分数据计算预测评分；最后选取预测排名靠前的若干项作为推荐结果返回给目标用户或项目，至此完成推荐［17］。

传统CF 算法存在的不足体现在以下两个方面：①生活中，用户兴趣会随着时间推移而发生改变，但传统CF 算法等同考虑商品不同时间段的评分，导致寻找近邻用户时推荐精确度降低；②热门商品评价人数多，在相似度计算中会影响推荐结果的精确度。

1.2 算法改进的相似度计算

相似度矩阵在计算时分为基于用户的相似度集合与基于商品的相似度集合。定义用户集合U={u1,u2,…um}，商品集合I={i1,i2,…i3}，可用1 个n×m 的用户—商品评分矩阵Hmn对商品相似度进行建模，构建的用户—商品评分矩阵Hmn如下：

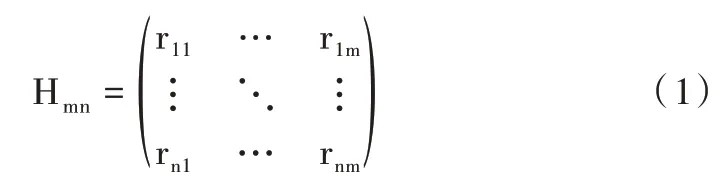
式（1）中，矩阵Hmn中的n 行代表n 个用户，m 列代表m个商品，第n 行m 列矩阵元素rnm表示第n 个用户对第m 个商品的评分。

项亮［18］引入热门商品与该商品的几何平均值以降低热门商品与其他商品的相似度，公式如下：

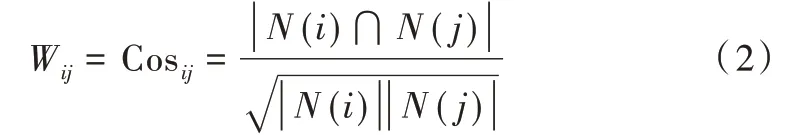
式（2）中，|N(i) |表示评价过商品i的用户集合，|N(j)|表示评价过商品j的用户集合，|N(i) ⋂N(j) |表示对商品i和商品j都有过评价的用户集合。

推荐系统不仅要反映出用户的近期偏好，还要预测其长期偏好。Breese 等［19］提出不活跃用户对商品相似度的影响大于活跃用户，因此在计算时要降低活跃用户对相似度权重的影响，即增加项，公式如下：

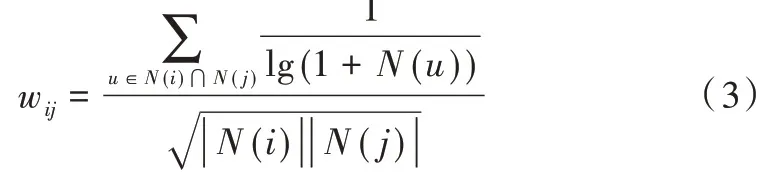
式（3）中，N(u)表示对商品u有过行为的所有用户。

近期行为最能反映出用户的当前兴趣，因此时间相隔较短的行为才能更好地反映商品之间的相似度，故在公式（3）中加上时间衰减衰减因子［20］，公式如下：

式（5）中，α为时间衰减因子的影响系数，用户兴趣变化越快，α的值越大，反之越小［21］。

由式（4）得到用户的最近行为，由于用户的最近行为与当前行为关系最大，因此计算用户对商品的评分时还应加上时间衰减函数最终得到用户u对商品j的偏好程度为：

式（7）中，t0为当前时间，rui为用户u对商品i的偏好程度，β为时间衰减因子。

2 实验设计

对本文提出的算法与传统CF 算法（余弦相似度）进行比较，分别在不同K 值（近邻用户数）和Top N 推荐长度下比较二者的精确度、召回率和F1 值，并对实验结果进行分析。

2.1 实验算法实现步骤

改进商品相似度算法步骤如下：

输入：用户—商品评分矩阵Hmn，近邻用户数K，商品返回数I，推荐列表长度N。

输出：用户推荐列表。

步骤1：在训练集中构建用户—商品评分矩阵Hmn。

步骤2：根据公式（3）计算加入物品惩罚因子的商品相似度矩阵wij。

步骤3：根据公式（4）加入时间衰减函数，计算用户最近的商品相似度矩阵wij，其中参数α设置为0.5。

步骤4：根据公式（6）得到最终用户当前对商品的相似度矩阵wij，其中参数β设置为0.8。

步骤5：遍历用户历史商品集合，从该集合中找出每个历史商品最相似的K 个商品作为候选集。

步骤6：从候选集合中选出指定返回数为I 的集合作为推荐结果。

2.2 实验准备

以电影评分作为实验对象，选取GroupLens 实验室成立的MovieLens 站点中的ml-1m 数据集。如表1 所示，该数据集包含6 040 个用户对3 900 部电影的评分记录，其中每个用户最少有20 条评分数据，共计1 000 209 条评分记录。评分划分为5 个等级，用1～5 的整数表示，评分数值越大表示该用户对电影的喜爱程度越高。该评分数据的稀疏度为1-1 000 209/（6 040×3 900）=0.956，两个时间衰减因子α和β分别设置为0.5 和0.8。数据集中还包含了用户个人信息和电影标签信息。

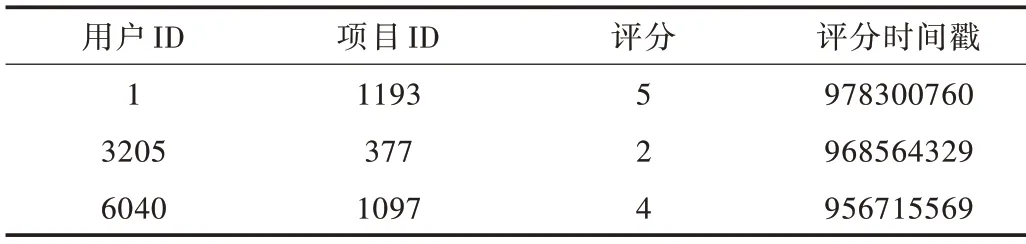
Table 1 Partial experimental data set表1 实验数据集部分展示

2.3 推荐指标

为评价算法性能，将整个MovieLens 数据集进一步拆分为不相交的两个部分，分别为训练集和测试集。为此，引入变量x 作为测试集占整个数据集的百分比，设定x=0.2，即在整个数据集中，训练集占80%，测试集占20%，训练集与测试集比例为8∶2［22］。利用不同K 值和Top N 算法比较精确度（Precision）、召回率（Recall）和F1-Score 的变化，在3 次试验下取评价指标的平均值作为实验结果。其中，N 为推荐列表中的商品总数，P 为目标用户在前N 项中的商品数。

其中，精确度定义：

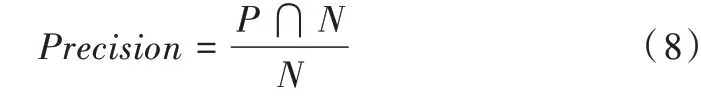
召回率定义：

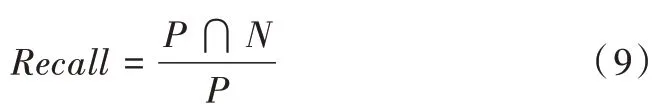
F1 定义：

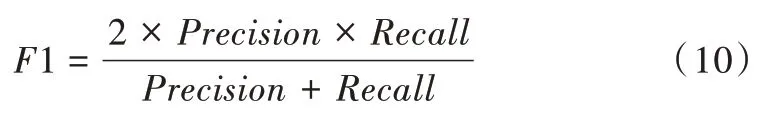
2.4 影响因素

影响算法结果的操作有3 个：①将两种不同相似度计算方法（余弦相似度、改进余弦相似度）应用到基于商品的CF 算法中；②使用不同K 值（近邻用户数）比较两种算法在不同K 值下的精确度和召回率；③使用不同Top N 算法的推荐长度，比较算法改进前后的精确度和F1-Score。考虑到加入时间衰减因子和惩罚因子后推荐商品的精确度，推荐列表不宜太长，因此本文将推荐列表长度设置为5、10、15、20。

2.5 实验结果与分析

2.5.1 余弦相似度算法改进前后商品偏好得分变化

在相同参数下，根据用户—商品评分矩阵计算相似度算法改进前后的商品偏好得分情况。以1196 号用户为例，在返回40 个商品的条件下，运用改进的余弦相似度算法计算1196 号用户对未评价商品的偏好分数为27.94，比传统余弦相似度算法得出的商品偏好分数（65.87）下降了37.93，具体如图1 所示。说明用户对商品的偏好程度是随着时间变化的，比较符合现实情况。

2.5.2 不同近邻用户数K 下算法的精确度和召回率

将改进相似度的算法称为New Item CF，传统的基于商品的CF 算法称为Item CF。在K 值（近邻用户个数）不同，物品返回数为40 的条件下，两种算法的精确度和召回率分别如图2、图3 所示。由图2 可知，New Item CF 的精确度明显高于Item CF，在K=200 时，New Item CF 的精确度达到最大，为0.18，比Item CF 的精确度提高了9%，二者差值也达到最大。由图3 可知，在相同条件下，New Item CF 的召回率明显高于Item CF，在K=200 时，New Item CF 的召回率达到最大，为0.17，比Item CF 提高了7.2%，二者差值也达到最大。

Fig.1 Score of items before and after similarity algorithm improvement图1 相似度算法改进前后物品得分

Fig.2 Precision comparison of recommendation results under different K values图2 不同K 值下推荐结果的精确度比较

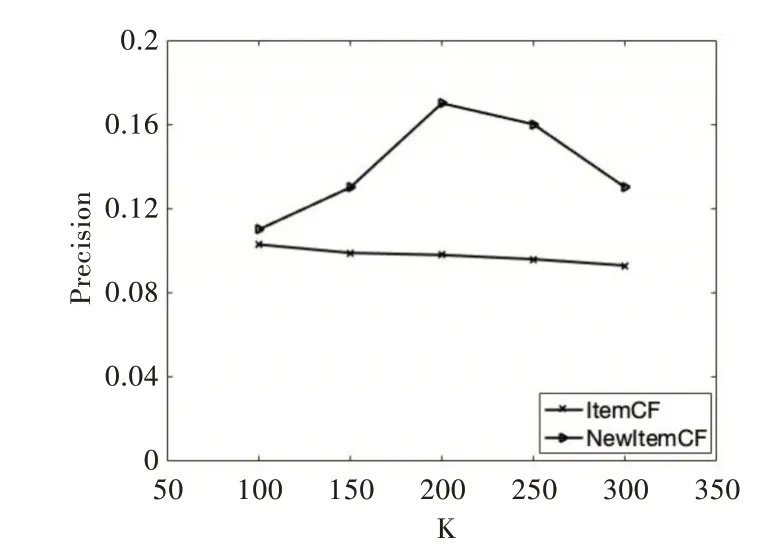
Fig.3 Changes of recall rate under different K values图3 不同K 值下召回率的变化

2.5.3 不同Top N 算法下精确度比较

将商品近邻数设置为40，通过设置不同推荐列表长度n 测试改进算法的精确度。由图4 可知，当推荐长度为5时，New Item CF 算法的精确度大于Item CF 算法。然而，随着推荐长度的增加，New Item CF 和Item CF 的精确度均开始下降，当Top N=10 时，Item CF 的精确度超过New Item CF。因此，在使用New Item CF 算法推荐商品时，推荐列表不宜过长。

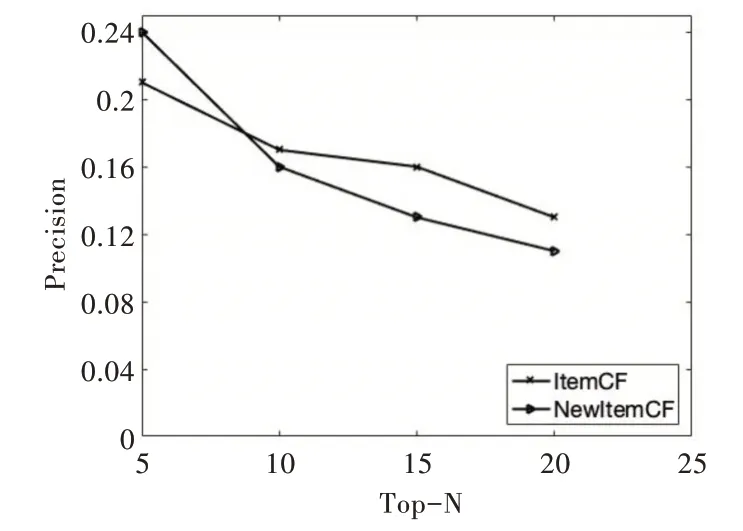
Fig.4 Precision under different Top-N algorithm图4 不同Top-N 算法下的精确度

2.5.4 不同Top N 算法下F1 值比较

将商品近邻数设置为40，通过设置不同推荐列表长度n 测试算法的F1 值。由图5 可知，当推荐长度<15 时，New Item CF 的F1 值大于Item CF。但随着推荐列表长度的增加，即当推荐长度>15 时，New Item CF 的F1 值小于Item CF。由此可知，加入时间衰减函数和物品惩罚因子后，随着推荐长度的增加，New Item CF 的推荐效果会差于Item CF。

Fig.5 F1 values for different Top-N algorithm图5 不同Top-N 算法下的F1 值

3 结语

在日常生活中，用户的兴趣爱好可能会随着时间推移而发生变化。本文针对用户的个性化需求将时间衰减函数和物品惩罚因子融入到相似度矩阵计算中，通过一系列数据证明，若实验参数设置得当，在一定条件下，改进的推荐算法在精确度、召回率和F1 值方面比传统CF 算法明显提高，但当推荐列表长度不断增加时，改进算法的精确度和F1 值开始下降，其性能开始弱于传统CF 算法。下一步研究重点：①在不降低推荐精确度的同时扩大推荐商品的范围，扩展用户兴趣面；②根据用户心情变化快慢赋予具体参数，表示用户当前不同的兴趣特点，以更加精确和实时地进行个性化推送。