预处理GPBi-CG 算法的数值保角变换计算法

石允龙，吕毅斌，王樱子，伍 康

（1.昆明理工大学 理学院；2.昆明理工大学 计算中心，云南 昆明 650500）

0 引言

保角变换是研究复变函数的重要方法之一，在物理学和工学中有着广泛应用，如流体力学、光学、空气动力学、图像处理等很多领域的实际问题中都有保角变换的身影［1-2］。1952 年，Nehari［3］给出了5 种狭缝域作为多连通域保角变换的重要规范域，分别是平行狭缝域、弧形狭缝域、径向狭缝域、带有弧形狭缝的圆盘域及带有弧形狭缝的圆环域，任何多连通域都可映射到这5 种规范域上；20 世纪80 年代，日本学者Amano 对模拟电荷法和数值保角变换作了大量研究，提出基于模拟电荷法的数值保角变换计算法（Amano 法）［4-6］；2007 年，Nasser 将求解保角变换问题转化为黎曼希尔伯特问题，并用带有广义Neumann kernel 的边界积分方程求解该问题［7-8］。国外研究学者们提出了许多保角变换的数值方法，但针对提高数值保角变换精度的研究较少。

目前国内许多学者针对不同类型问题域的数值保角变换，提出一些提高模拟电荷法计算精度的方法［9-11］，但针对提高有界多连通区域数值保角变换精度的研究很少。因此，本文通过基于模拟电荷法的数值保角变换法将有界多连通区域映射到有相同圆心的带有弧形狭缝的圆环，并给出提高该问题域数值保角变换计算精度的算法。

本文首先介绍基于模拟电荷法的有界多连通区域数值保角变换算法，由于该方法产生的约束方程组有很强的病态性，因此根据预处理思想［12］，采用1-范数均衡法处理约束方程组，使矩阵所有行或列有相同的模，降低矩阵的条件数，从而改善矩阵的病态性［13］；然后，通过基于双共轭梯度的广义乘积型算法（GPBi-CG）［14］求解预处理后的约束方程组，得到更高精度的方程组数值解，即保角变换的模拟电荷与变换半径，进而得到近似保角变换函数；最后，通过数值实验验证了本文提出的数值保角变换新算法的优越性。

1 相关研究

1.1 有界多连通区域保角变换函数

本节主要阐述基于模拟电荷法的有界多连通区域的数值保角变换计算法［15-16］。图1 是多连通域保角变换的重要规范域之一，即将有界多连通区域D映射到带有弧形狭缝的圆环域E上。其中，问题域D由z平面上的闭合Jordan曲线C1,C2,…,Cn构成，且闭合曲线C2,…,Cn被闭合曲线C1包围；目标域E由w平面上的单位圆S1、同心圆S2以及与圆环有相同圆心的弧形狭缝S3,…,Sn构成，即带有圆弧狭缝的单位圆环。

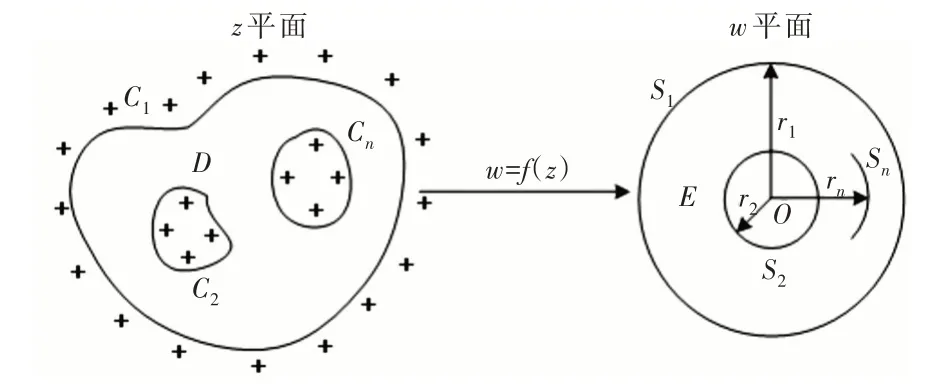
Fig.1 Numerical conformal mappings of bounded multiply connected domains by the charge simulated method（“+”denoted the position of charge points）图1 基于模拟电荷法的有界多连通区域数值保角变换（“+”表示模拟电荷点位置）

由Riemann 映射定理可知，在满足正则化条件f(u)=0,f(v)=1，u和v为正则化点，且点u在闭合曲线C2内部，点v是曲线C1上的点时，从多连通域D到规范狭缝域E存在唯一的保角映射函数w=f(z)，将曲线C1,C2,…,Cn分别映射成圆或圆弧狭缝S1,S2,…,Sn。

根据保角变换的几何性质，可得到边界约束条件：

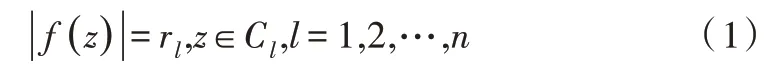
其中，r1,r2,…,rn是圆与圆弧狭缝的半径，且r1=1。

在不失一般性的情况下，不防令z=0 在曲线C2内部，且f(0)=0，利用调和函数g(z)及其共轭调和函数h(z)，将有界多连通区域D映射到典型狭缝域E的保角变换函数表示为：

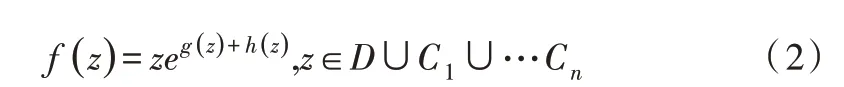
再根据正则化条件中f(v)=1，得：

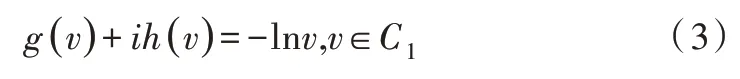
由边界约束条件，得：

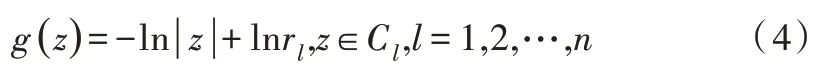
根据保角变换函数存在的唯一性，本文将求解映射函数f(z)问题转化为求解调和函数g(z)与h(z)的问题。

1.2 基于模拟电荷法的有界多连通区域数值保角变换

模拟电荷法通过复对数函数的线性组合近似调和函数g(z)与h(z)，即：

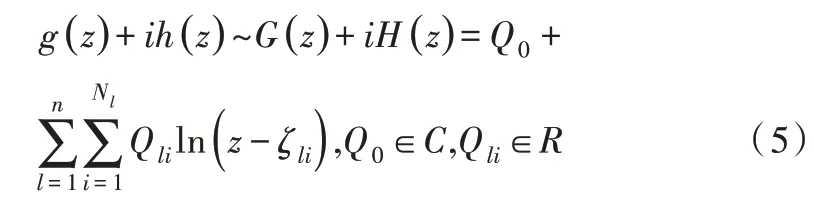
其中，Q0为复常数，Qli为未知电荷。如图1 所示，模拟电荷点ζli在区域D外部，即N1个模拟电荷点分布在边界C1外部，剩余的N2,…,Nn个模拟电荷点分别分布在边界C2,…,Cn内 部。

因为G(z)、H(z)分别是g(z)与h(z)的近似映射函数，所以由式（3）、式（4）可知：

其中，Ri是ri的近似，zmk是边界曲线Cm上的约束点。通过式（7）计算出Q0并代入式（5），得：

联立式（6）与式（8），有：

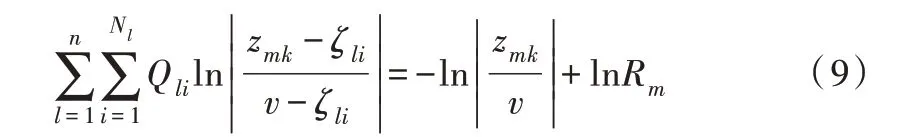
由于保角变换函数具有单值性与伸缩率不变性［17-18］，近似映射函数也应满足相应性质，从而有：

通过解式（9）、（10）与（11）联立所得的N1+N2+…+Nn+n阶大型线性方程组，得到电荷Qli,l=1,…,n,i=1,…,Nl和变换半径Rm,m=1,…,n的值，从而求得保角变换近似函数：

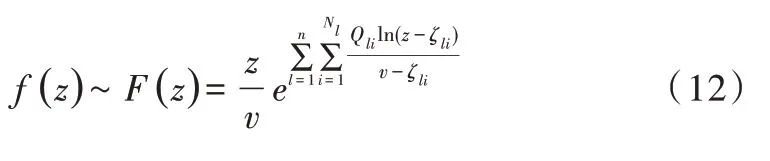
2 本文方法

2.1 1-范数均衡法

将由式（9）、（10）与（11）联立所得的N(=N1+N2+…+Nn+n)阶大型线性方程组写成Ax=b的形式。因为该方程为非对称病态方程，所以本文首先基于1-范数均衡法降低方程组的条件数，再采用GPBi-CG 迭代算法求解预处理后的线性方程组。

对线性方程组Ax=b两边同乘以矩阵U，且令x=Bx*，得：

式中，U、B为对角矩阵，且矩阵U的对角元素为uii=,i=1,2,…,N，矩阵B的对角元素为bjj=,j=1,2,…,N，其中S与T为任意常数。矩阵A左乘U后可使每行的1-范数相同，矩阵UA再右乘B后每列的1-范数相同。行列的1-范数均衡可连续重复下去，一般经过几次重复后，系数矩阵的条件数则不再改变，方程的病态性也不再得到改善，此时可停止重复，得到最后经过预处理的线性方程：

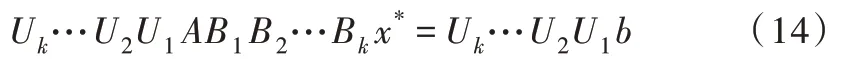
2.2 基于预处理的GPBi-CG 算法

将式（14）改写为：

其中，A*=Uk…U2U1AB1B2…Bk,b*=Uk…U2U1b。

利用GPBi-CG 算法求解得到x*，再由x=B1B2…Bk x*得到原方程组的解x，该方法称为基于预处理的GPBi-CG算法。GPBi-CG 算法不仅避免了双共轭梯度法（Bi-CG）中使用转置矩阵生成Krylov 子空间，从而需要进行的转置矩阵与向量乘法运算，而且提高了收敛速度。

根据文献［19］、［20］，可得到求解线性方程组的Bi-CG算法。算法具体步骤如下：

根据文献［14］可知，GPBi-CG 算法是在Bi-CG 算法基础上，通过使用Bi-CG 算法的残差多项式Rn与其它具有标准三项递推关系的多项式Hn乘积，定义新算法的残差多项式，并且由Rn的三项递推关系：

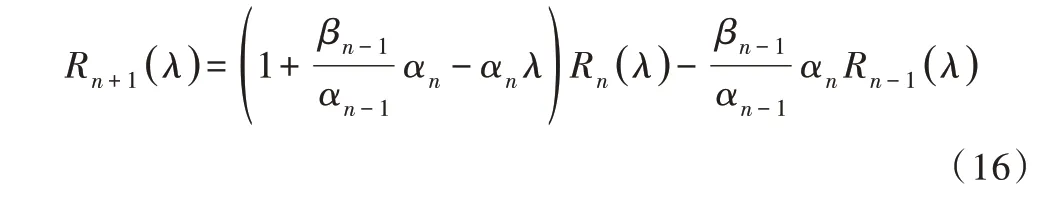
给出Hn的三项递推关系：

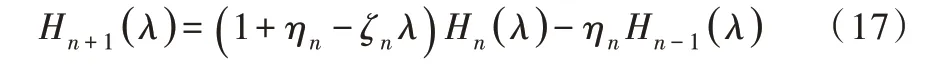
其中，参数ηn与参数ζn可由残差的最小二范数来确定，即：

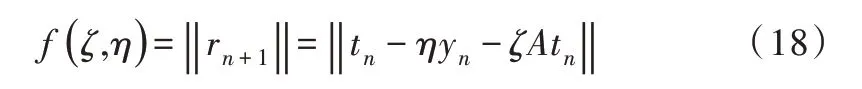
由这两组多项式的乘积得到相应的多项式递推关系，从而得到新算法，即GPBi-CG 算法的递推公式。

最后本文参考文献［21］的思想，将1-范数均衡预处理与GPBi-CG 算法相结合，建立求解模拟电荷与变换半径的预处理GPBi-CG 算法。算法具体步骤如下：

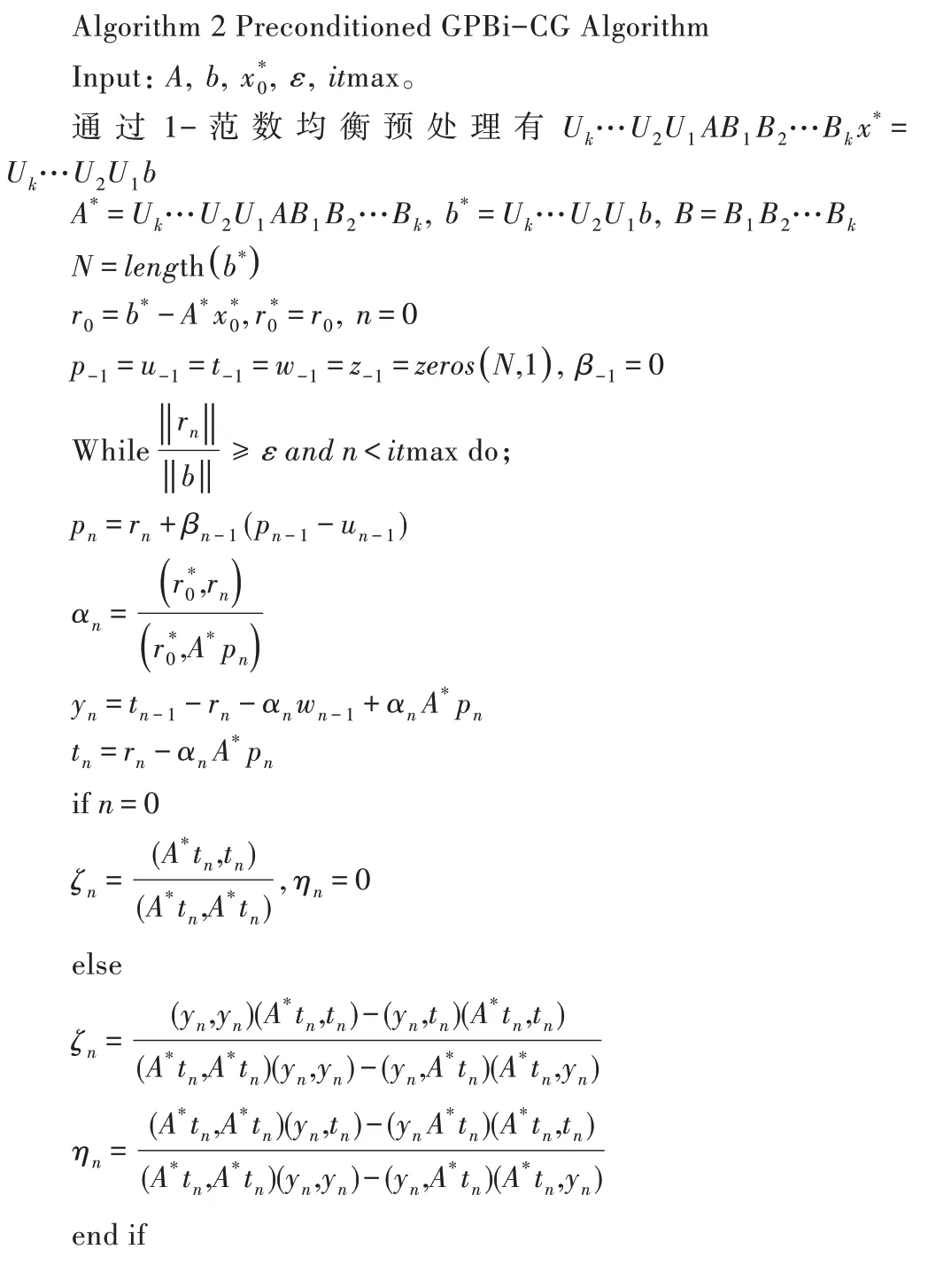
3 数值实验

本文通过以下两个基于模拟电荷法的有界多连通区域保角变换数值实验检验本文方法，即基于预处理的GP⁃Bi-CG 算法相比Gauss-Seidle 法［22-23］与Amano 法的优越性，并使用MATLAB 软件编写程序。

基于模拟电荷法的数值保角变换根据拉普拉斯方程最大值原理在边界上进行误差评价，误差计算公式为：

例1：多连通区域D以正方形C1为外边界，以正方形C2、C3为内边界，其边界曲线方程为：

约束点为：

模拟电荷点为：

剩余约束点与模拟电荷点按照轴对称配置即可。

图2 为当Nl=56(l=1,2,3)时问题域边界及模拟电荷点位置图，图3 是图2 基于本文方法的保角变换图。

表1 给出了取不同数量（32、56、80、104、120）的模拟电荷点时，本文方法与Gauss-Seidel 法及Amano 法的对比，包括误差、迭代次数及条件数情况。从表1 可以看出，本文方法经过预处理后，方程组的条件数降低到传统方法条件数的左右。对于内、外边界Cl，本文方法的误差明显小于Gauss-Seidel 法，且迭代次数远少于Gauss-Seidel 法；对于外边界C1，本文方法的误差明显小于Amano 法，充分验证了本文方法的优越性。

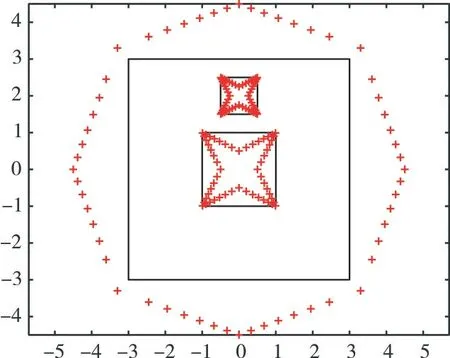
Fig.2 Boundary and position of charge points（example 1）图2 边界及模拟电荷点位置（例1）

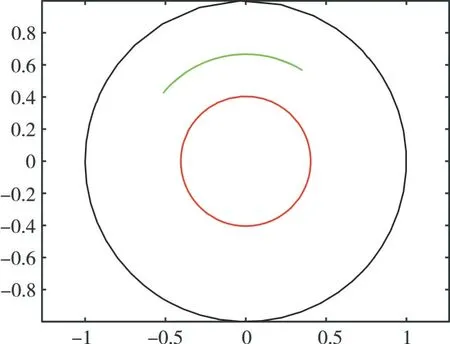
Fig.3 Fig.2 Transformation diagram based on the proposed method（example 1）图3 图2 基于本文方法的保角变换图（例1）

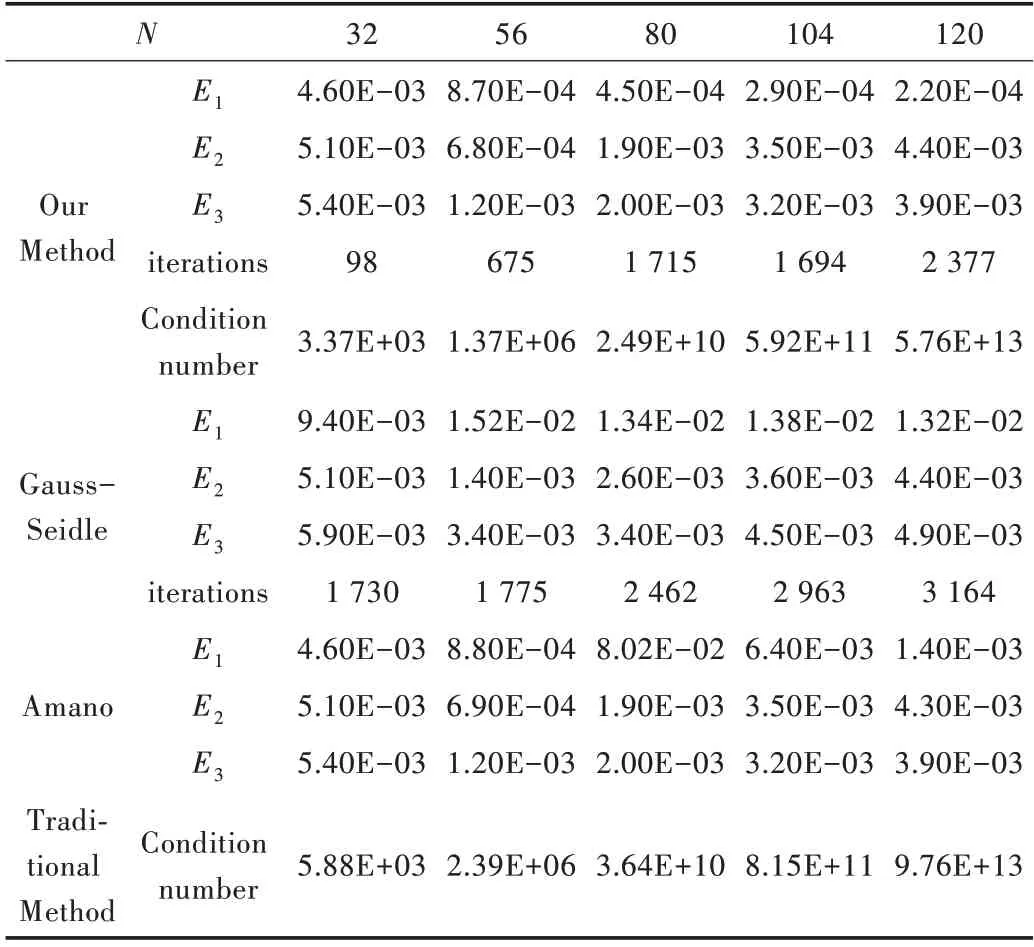
Table 1 Numerical conformal mapping error，iterations and condi⁃tion number（example 1）表1 数值保角变换误差、迭代次数与条件数（例1）

图4 给出了3 种方法更直观的误差曲线图。结合表1与图4 可以看出，当各边界模拟电荷点数N=104 时，边界曲线C1基于本文方法的误差为E1=2.90 × 10-4，迭代次数为1 694 次；Gauss-Seidel 法的误差为E1=1.38 × 10-2，迭代次数为2 963 次；Amano 法的误差为E1=6.40 × 10-3，且本文算法随着模拟电荷点的增加，误差稳定下降。

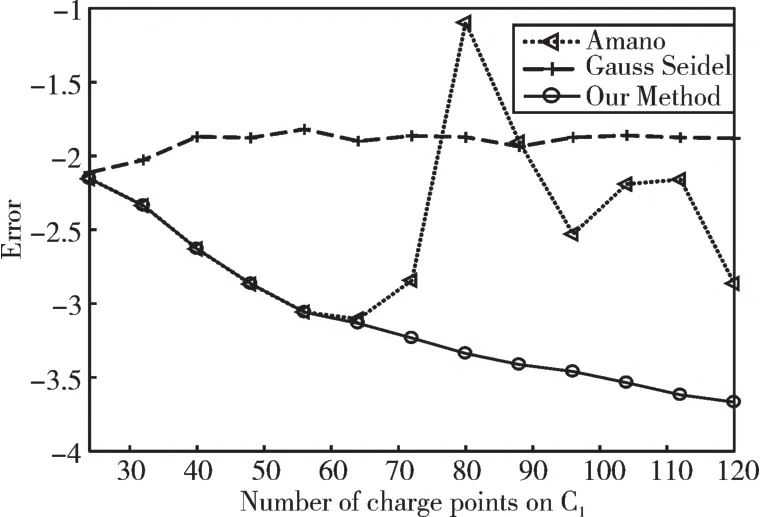
Fig.4 Error curve of conformal mapping（example 1）图4 保角变换误差曲线（例1）

为了进一步验证本文算法的有效性，下面以菱形为外边界的有界多连通区域的保角变换情况为例进行说明。

例2：多连通区域D以菱形C1为外边界，以正方形C2和C3为内边界的边界曲线方程为：

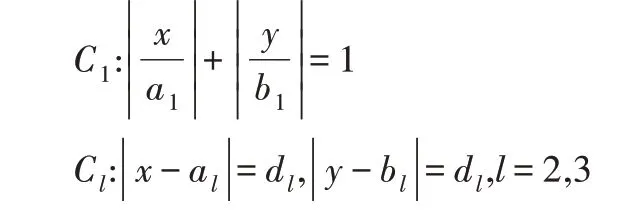
约束点位置为：

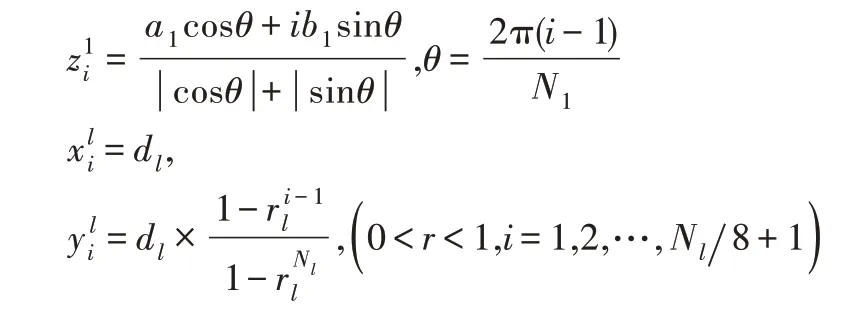
模拟电荷点位置为：

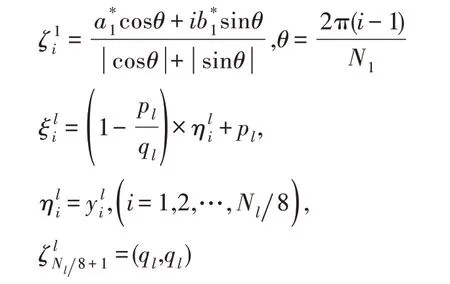
内边界C2、C3剩余约束点与模拟电荷点同样按照轴对称配置即可。

同样的，图5 为当Nl=56(l=1,2,3)时问题域边界及模拟电荷点分布图，图6 是图5 基于本文方法的保角变换图。

表2 同样给出了取不同数量（32、56、80、104、120）的模拟电荷点时，本文方法与Gauss-Seidel 法及Amano 法的对比，包括误差、迭代次数与方程组条件数情况。由表2 可知，本文方法经过预处理后，方程组的条件数降低到传统方法条件数的左右，且对于内、外边界Cl，本文方法的误差明显小于Gauss-Seidel 法，且迭代次数远少于Gauss-Seidel 法；对于外边界C1，本文方法的误差明显小于Amano法，再次验证了本文方法的优越性。

Fig.5 Boundary and position of charge points（example 2）图5 边界及模拟电荷点位置（例2）

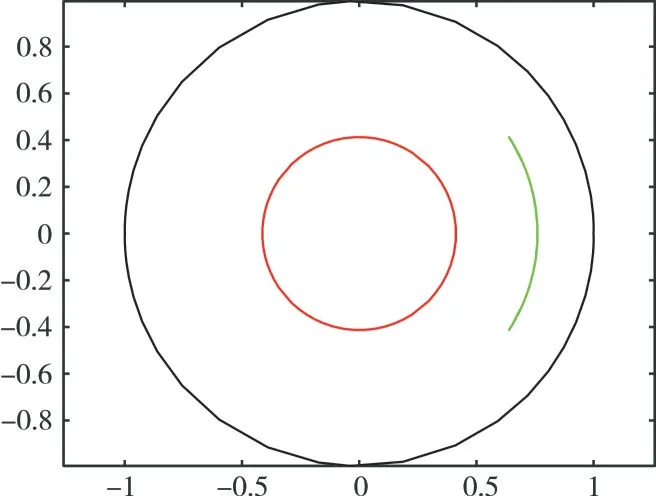
Fig.6 Fig.5 Transformation diagram based on the proposed method（example 2）图6 图5 基于本文方法的保角变换图（例2）

Table 2 Numerical conformal mapping error，iterations and condi⁃tion number（example 2）表2 数值保角变换误差、迭代次数与条件数（例2）

同样的，本文通过图7 给出了3 种方法更直观的误差曲线图。结合表2 与图7 可以看出，当各边界模拟电荷点数N=104 时，边界曲线C1基于本文算法的误差为E1=8.50×10-4，迭代次数为44 次；Gauss-Seidel 法的误差为E1=4.50×10-2，迭代次数 为3 300 次；Amano 法的 误差为E1=3.31×10-2，且本文算法随着模拟电荷点的增加，误差稳定下降，再次验证了本文算法的优越性。

Fig.7 Error curve of conformal mapping（example 2）图7 保角变换误差曲线（例2）

4 结语

本文提出基于1-范数均衡预处理GPBi-CG 算法的有界多连通区域数值保角变换计算法，并通过多个数值实验验证了该方法在算法精度、稳定性与迭代次数上都有较好表现，对于求解该类型问题域的近似保角变换函数具有明显的优越性。保角变换在图像处理中有着广泛应用，未来可进行一些具体应用的研究，比如本文研究结果可应用于将不规则或破损图片映射形成环形，并进一步将这些图片信息刻录到光学媒介、CD 或DVD 上长久保存下来。但不足的是，本文算法在剩余的4 种规范域、单连通域和双连通域等数值保角变换问题中的应用效果还有待验证，且本文是根据经验选取模拟电荷点，在未来研究中也可考虑给出更科学的选取方法。