特殊四边形动点问题的解题策略
2021-09-27漆发明
漆发明

动点几何问题是中考的热点题型,解决此类问题的基本策略是:动中取静——在运动变化中探索问题中的不变性(这里的“静”就是问题中的不变量、不变关系);动静互化——抓住“静”的瞬间,将一般情形转化为特殊问题,从而找到“动”与“静”的关系;以动制动——建立图形中的数量关系,进而解决问题.下面以特殊四边形动点问题为例进行介绍.
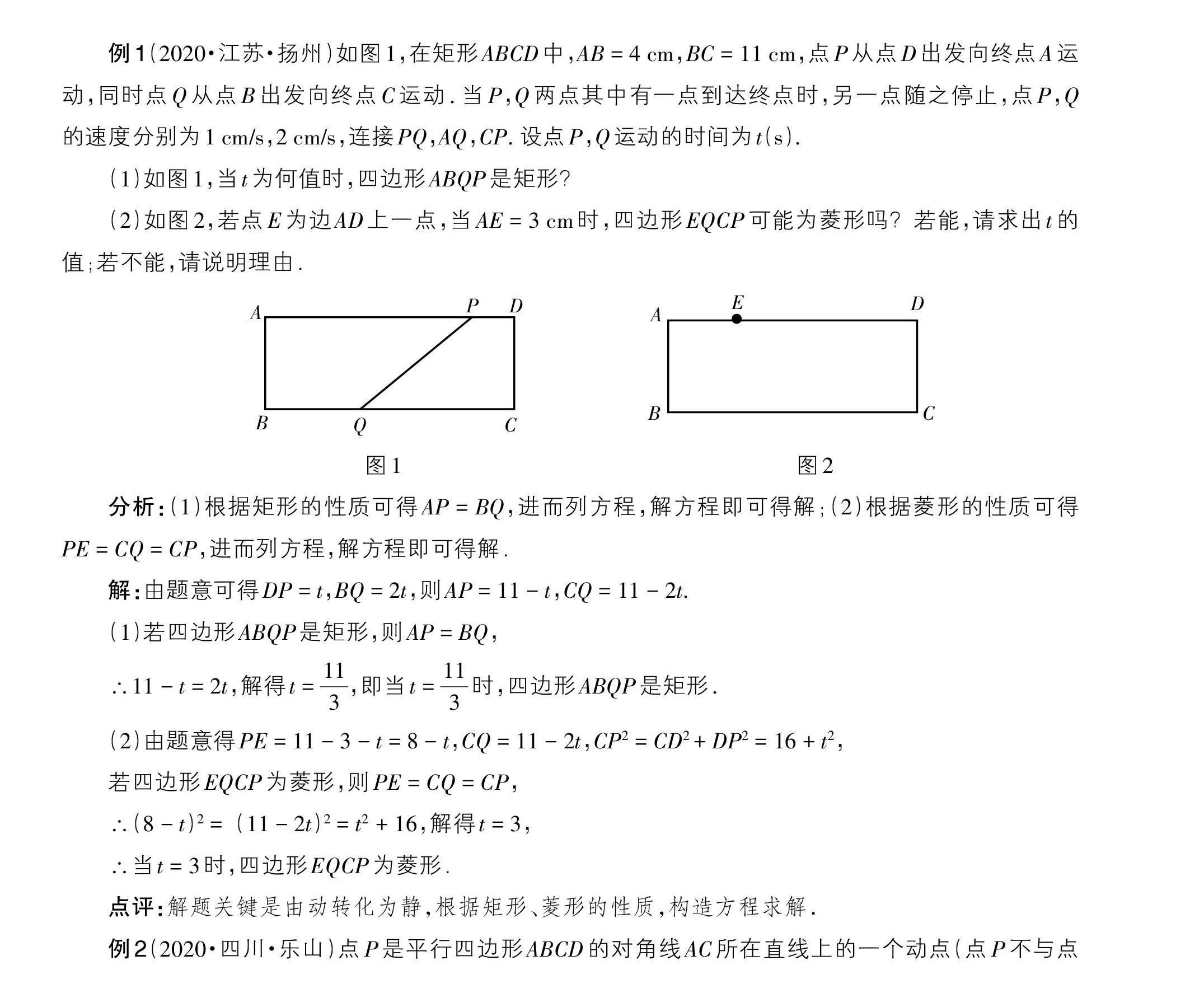
例1(2020·江苏·扬州)如图1,在矩形ABCD中,AB = 4 cm,BC = 11 cm,点P从点D出发向终点A运动,同时点Q从点B出发向终点C运动. 当P,Q两点其中有一点到达终点时,另一点随之停止,点P,Q的速度分别为1 cm/s,2 cm/s,连接PQ,AQ,CP. 设点P,Q运动的时间为t(s).
(1)如图1,当t为何值时,四边形ABQP是矩形?
(2)如图2,若点E为边AD上一点,当AE = 3 cm时,四边形EQCP可能为菱形吗?若能,请求出t的值;若不能,请说明理由.
[A][P][D][C][Q][B][E] [A][D][B][C]
图1 图2
分析:(1)根据矩形的性质可得AP = BQ,进而列方程,解方程即可得解;(2)根据菱形的性质可得PE = CQ = CP,进而列方程,解方程即可得解.
解:由题意可得DP = t,BQ = 2t,则AP = 11 - t,CQ = 11 - 2t.
(1)若四边形ABQP是矩形,则AP = BQ,
∴11 - t = 2t,解得t = [113],即当t = [113]时,四边形ABQP是矩形.
(2)由题意得PE = 11 - 3 - t = 8 - t,CQ = 11 - 2t,CP2 = CD2 + DP2 = 16 + t2,
若四边形EQCP为菱形,则PE = CQ = CP,
∴(8 - t)2 = (11 - 2t)2 = t2 + 16,解得t = 3,
∴当t = 3时,四边形EQCP为菱形.
点评:解题关键是由动转化为静,根据矩形、菱形的性质,构造方程求解.
例2(2020·四川·乐山)点P是平行四边形ABCD的对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为点E,F,点O为AC的中点.
(1)如图3,当点P与点O重合时,线段OE和OF的关系是 .
(2)当点P运动到如图4所示的位置时,请在图中补全图形并通过证明判断(1)中的结论是否仍然成立.
(3)如图5,点P在线段OA的延长线上运动,当∠OEF = 30°时,试探究线段CF,AE,OE之间的关系.
[D] [A][C][B][P][E][O][F] [D][A][C][B] [O] [D][A][C][B] [P][O][E][F][P]
图3 图4 图5
分析:(1)由“AAS”可证△AEO ≌ △CFO,可得OE = OF;(2)如图6,延长EO交CF于点G,由“ASA”可证△AOE ≌ △COG,可得OE = OG,由直角三角形的性质可得OG = OE = OF;(3)如图7,延长EO交FC的延长线于点H,由全等三角形的性质可得AE = CH,OE = OH,由直角三角形的性质可得HF = [12]EH = OE,可得结论.
解:(1)∵四边形ABCD是平行四边形,∴AO = CO,
∵∠AEO = ∠CFO = 90°,∠AOE = ∠COF,∴△AEO ≌ △CFO(AAS),
∴OE = OF.
(2)补全图形如图6所示. [A][E][D][C][G][B][F][P][O] [D][C][H][O][A][P][E][B][F]
图6 图7
结论仍然成立.
理由:延长EO交CF于點G,∵AE⊥BP,CF⊥BP,∴AE[⫽]CF,∴∠EAO = ∠GCO,
∵点O为AC的中点,∴AO = CO,又∵∠AOE = ∠COG,∴△AOE ≌△COG(ASA),
∴OE = OG,∵∠GFE = 90°,∴OF = [12]EG = OE.
(3)线段CF,AE,OE之间的关系为OE = CF + AE,
证明:如图7,延长EO交FC的延长线于点H,
由(2)可知△AOE ≌△COH,∴AE = CH,OE = OH,
∵∠OEF = 30°,∠HFE = 90°,∴HF = [12]EH = OE,
∴OE = CF + CH = CF + AE.
即OE = CF + AE.
点评:解题关键是添加辅助线构造全等三角形.
