2021年玛多MS7.4地震的震后效应模拟
2021-09-27谈洪波王嘉沛杨光亮陈正松吴桂桔申重阳黄金水
谈洪波 王嘉沛 杨光亮 陈正松吴桂桔 申重阳 黄金水
1)中国科学技术大学,地球和空间科学学院,合肥 230026 2)中国地震局地震研究所,武汉 430071
0 引言
地震发生后,中国地震局迅速组织实施了地震科学考察,开展了多手段联合观测(包括重力和GNSS等),为震后地震趋势判定、 地震应急救援等工作提供资料。 震源理论的发展及观测数据的不断丰富,使我们可在地震发生后快速确定震源的基本参数,也使得将地震位错理论应用于震后趋势分析成为可能。 Zhang等(2014)发展了一套反演地震破裂过程的迭代反褶积方法,并联合高频GPS和强震数据对日本MW9.0地震的破裂过程进行了反演。 刘刚等(2015)利用远场地震波和GPS数据给出了2015年尼泊尔MS8.1地震的破裂过程。 Feng等(2017)利用InSAR和GPS数据反演了2015年尼泊尔MW7.8地震及其MW7.2余震的断层滑动分布。 谈洪波等(2013)模拟了玉树MS7.1地震的同震重力变化并利用绝对重力观测结果进行了检验。 Zhang等(2016)对日本MW9.0地震的同震模拟结果及观测形变、 重力变化进行了比较,发现两者符合较好。 Riguzzi等(2019)模拟了均匀弹性半空间中2009—2016年意大利中部4次MW6地震的同震重力效应,并就模拟结果进行了合理解释。 但实际地球要复杂得多,地球曲率、 层状构造、 黏滞性、 自重效应、 三维构造等均会对计算结果产生不同程度的影响(Pollitz,1996; Sunetal.,2002; 孙文科,2008,谈洪波等,2010)。 同震只是介质在完全弹性情况下的瞬时效应,对于长时间尺度的震后效应而言,其形变和重力变化有可能完全改变同震效应的形态,利用震后数据获取断层和地球内部信息也是非常有意义的研究内容(张晁军等,2008; 贺鹏超等,2018; 赵斌等,2020)。 因此,本文将采用更为接近实际情况的弹性—黏弹分层介质模型,并考虑自重的影响,从形变和重力的角度对该地震的同震及其震后效应进行理论模拟,为利用实际形变和重力资料解释此次地震孕震过程(包括同震和震后)的相关研究提供理论依据。
1 理论基础
均匀弹性半无限空间地球模型的位错理论由Okada(1985)和Okubo(1992)完善和发展。 假设地震破裂发生在一个平面上,断层如图 2 所示,长宽分别为L和W,倾角为δ; 断层底部深度为d; 断层面上的走滑、 倾滑和张裂方向错动量分别为U1、U2、U3,在地表(x1,x2,0)处引起的形变Δu和重力变化Δg可分别表示为(Okada,1985; Okubo,1992)

图1 研究区主要构造分布Fig. 1 Distribution of the main structures in the study area.黑点为截至2021年5月30日的ML>2余震
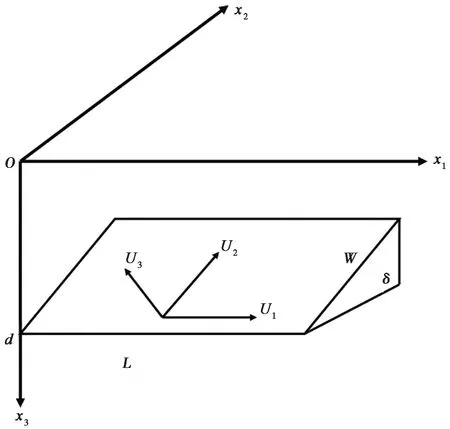
图 2 矩形断层位错模型示意图Fig. 2 Dislocation model of a rectangle fault.
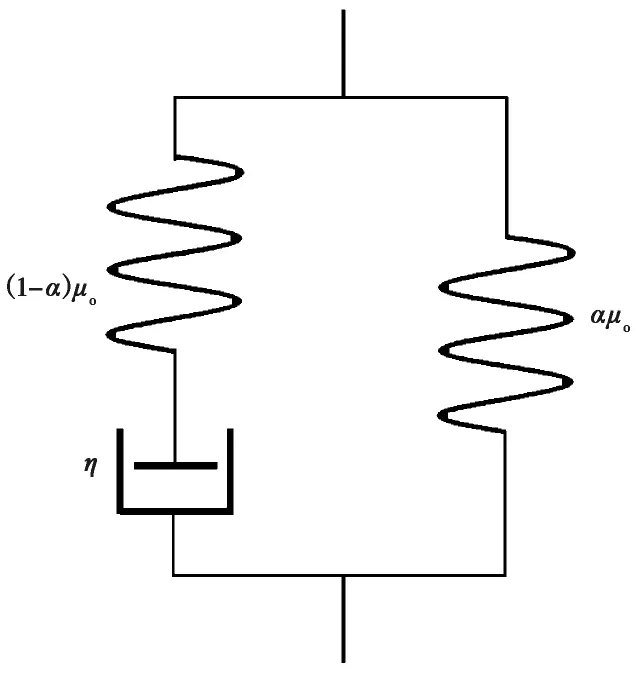
图 3 SLS流变模型Fig. 3 The SLS rheological model.
(1)
Δg(x1,x2)={ρG[U1Sg(ξ,η)+U2Dg(ξ,η)+U3Tg(ξ,η)]+ΔρGU3Cg(ξ,η)}‖-βΔh(x1,x2)
(2)
其中,G为万有引力常数;ρ、 Δρ分别为介质密度、 张裂纹内密度与介质密度之差;S(ξ,η)、D(ξ,η)、T(ξ,η)和Sg(ξ,η)、Dg(ξ,η)、Tg(ξ,η)、Cg(ξ,η)为系数; 自由空气重力梯度β=0.309×10-5m/s2,Δh为地表高程变化,Chinnery记号‖表示置换(Okada,1985)。
考虑地球自重影响时,Rundle(1980)首次给出了基于无限小静态形变理论动力平衡方程:
·Γ+ρψ+u·g-g(ρu)=0
(3)
(4)
Γ=(λ·u)I+μ[u+(u)T]
(5)
式中,λ为拉梅常数;μ为切变模量;I为单位张量。 根据Adams-Williamson条件(Longman,1963),方程(3)可变换为(Wangetal.,2006)
Γ+ρguz-(ρ
(6)
对于黏弹介质,一般基于弹性-黏弹线性对应原理(Fung,1965): 黏弹体在频率域的应力-应变关系与弹性体在时间域的一致,故在频率域中黏弹问题可采用弹性问题的处理方式计算后再通过逆傅里叶变换回到时间域(Matsuuraetal.,1981)。 Wang等(2006)采用SLS(Standard Linear Solid)流变体将弹性体和黏弹性体用统一的模型表示(图 2),这时复切变模量和复拉梅常数可表示为
(7)
(8)

联合方程(5)—(8),根据正则化Haskell(1953)传播算法,可将边值问题转变成代数问题,根据给定的地球参数求出频率域中对应的格林函数(即单位点脉冲位错响应),再采用抗假频技术(Kindetal.,1982)对频率域中的格林函数进行傅里叶逆变换回到时间域,最后通过式(1)和(2)的线性叠加求出地表形变和重力变化( Wang,1999; Wangetal.,2006)。
2 介质模型和发震断层模型
前期的研究结果表明地壳分层对地表同震效应的影响可达20%以上(Sunetal.,2002; 孙文科,2008; 谈洪波等,2010),因此需要考虑垂向分层结构。 本文参考Crust1.0(4)https:∥igppweb.ucsd.edu/~gabi/crust1.html。地壳模型,将研究区地球分为上、 中、 下地壳和上地幔,具体参数见表1。 此外,也考虑了下地壳和上地幔介质的黏滞性,黏滞系数η参考张晁军等(2008)、 贺鹏超等(2018)和赵斌等(2020)对青藏高原的研究结果。

表1 地壳—上地幔介质分层结构模型Table1 The layered structure of the crust-upper-mantle based on Crust 1.0
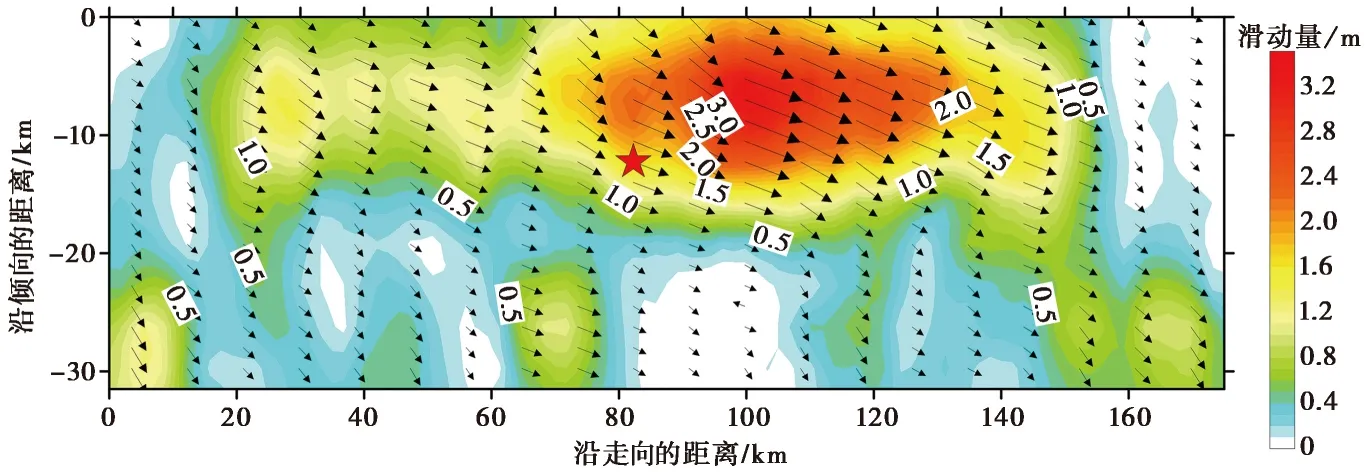
图4 断层滑动分布(据USGS结果绘制)Fig. 4 The slip distribution on the fault plane(according to USGS results).
3 同震效应
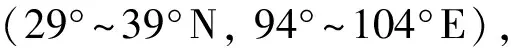
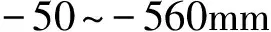
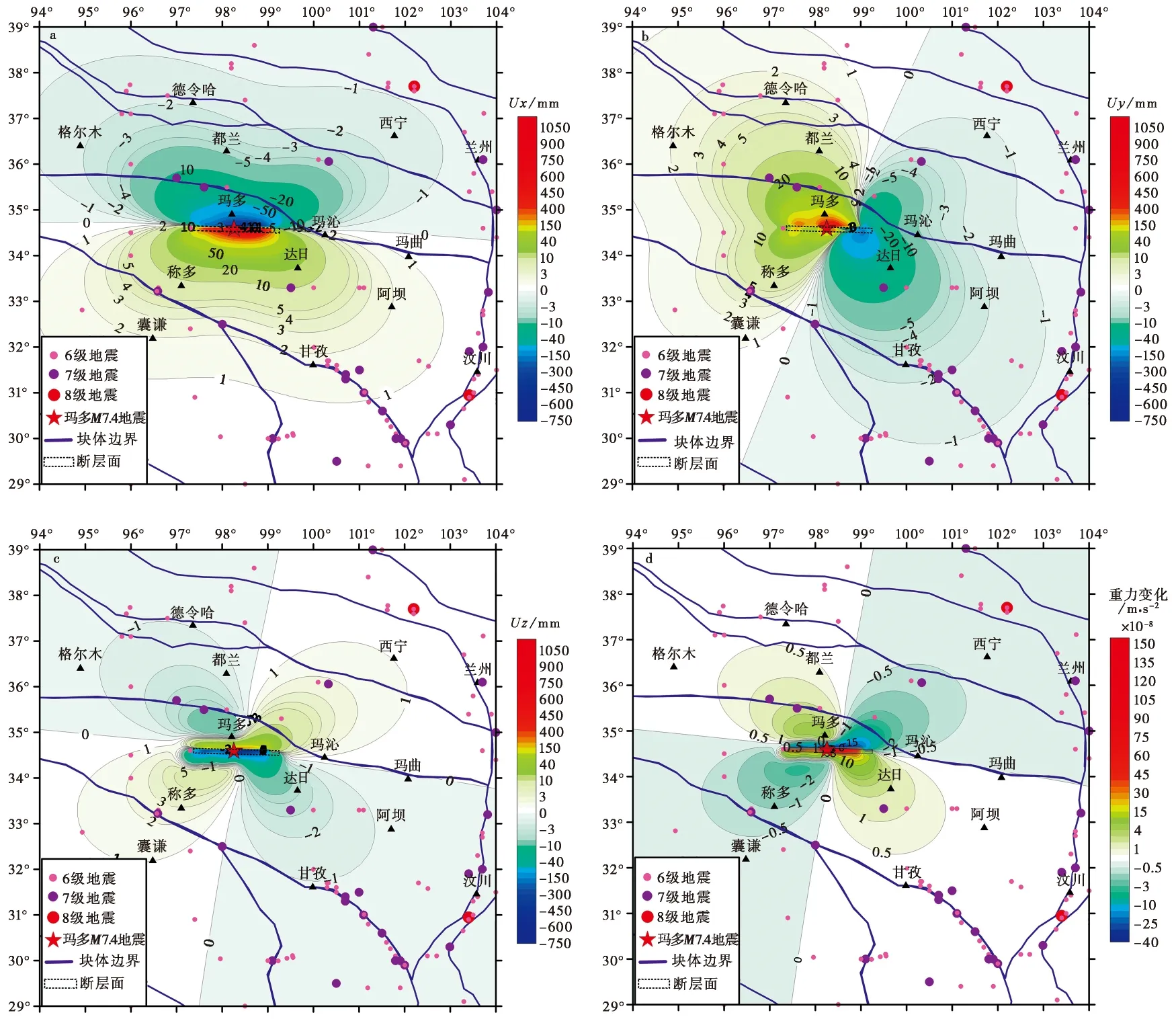
图5 地表同震效应Fig. 5 Surface co-seismic effects.a 经度方向位移; b 纬度方向位移; c 垂直位移; d 重力变化
4 震后效应

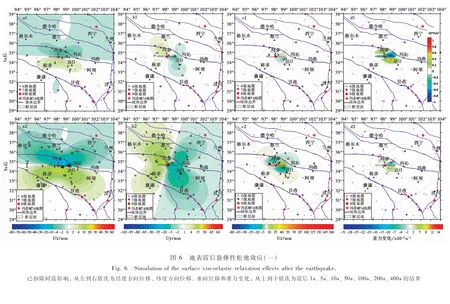
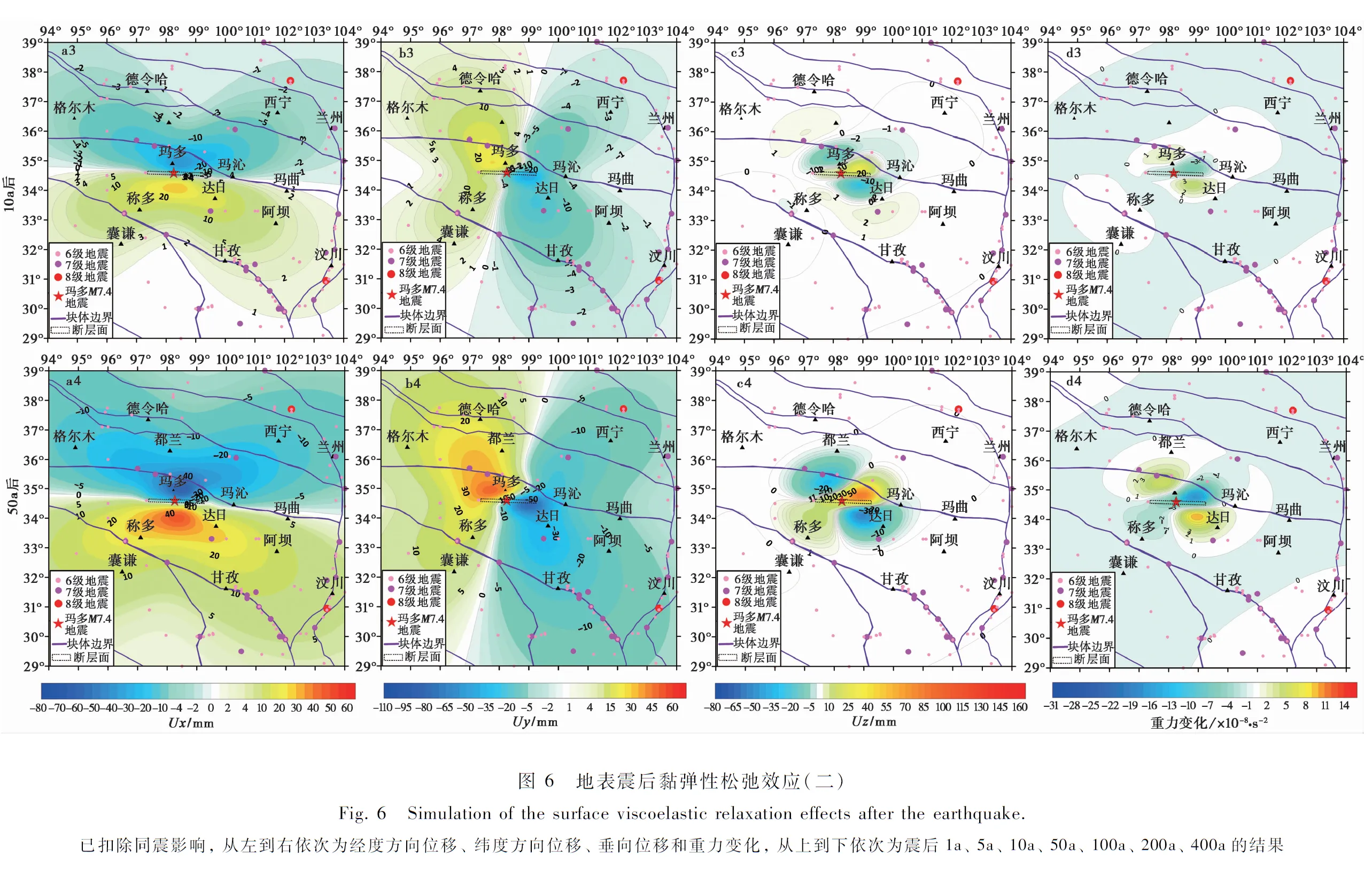
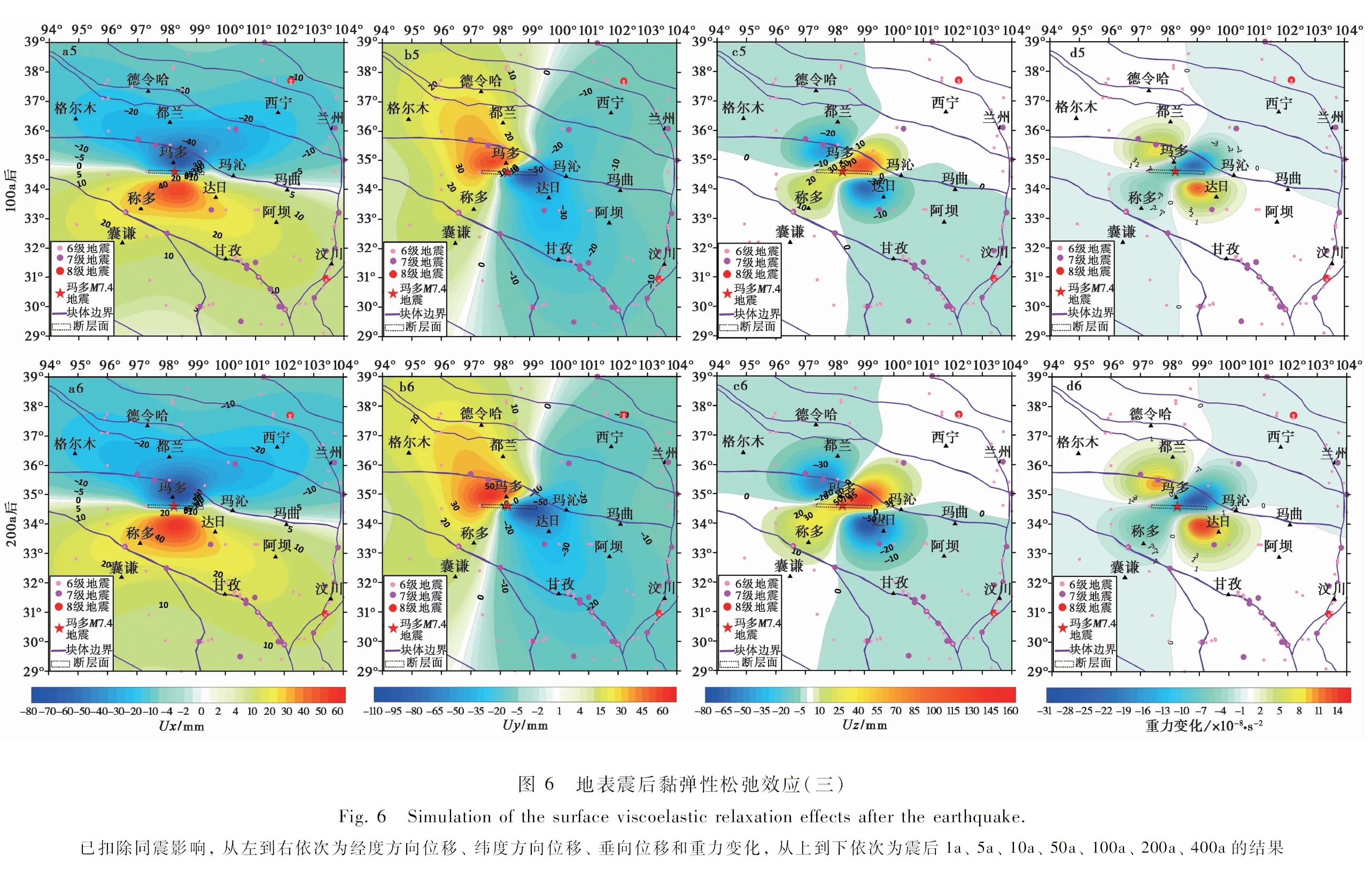
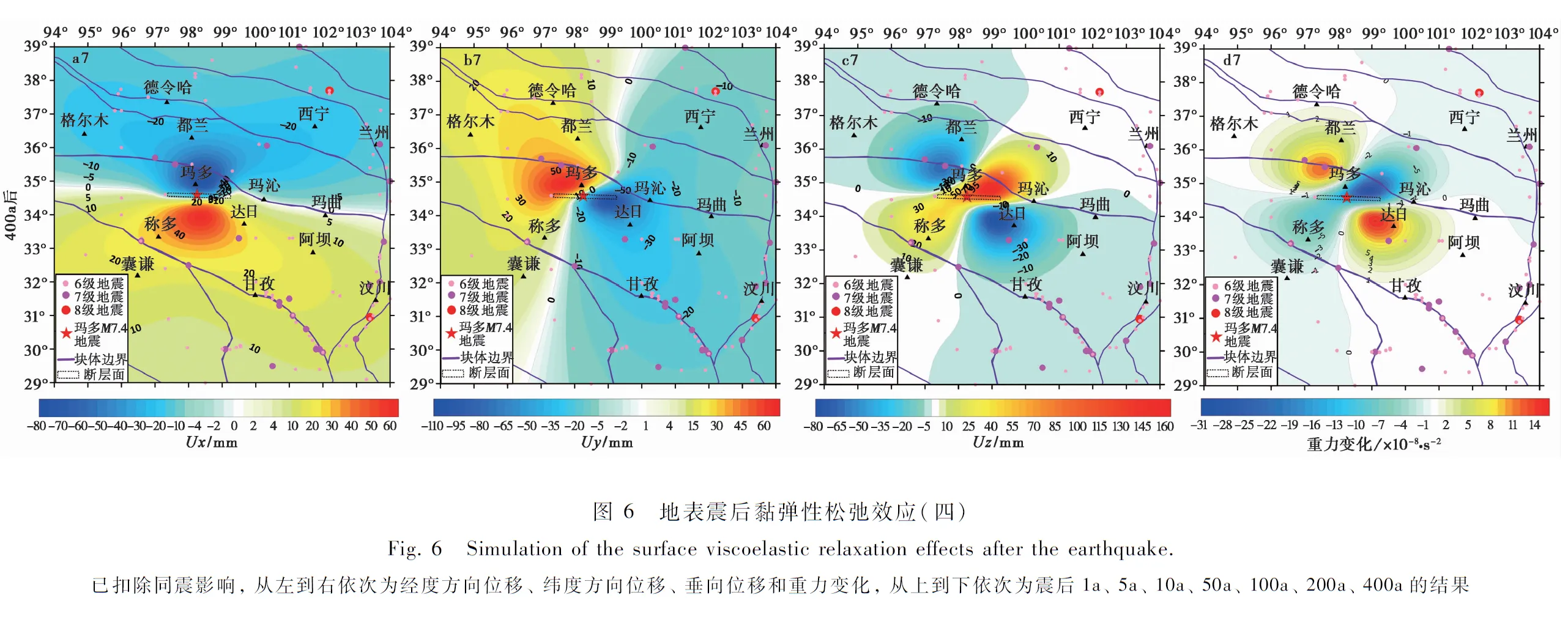
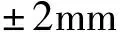
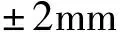
同时我们也对玛多、 称多和达日县城处的震后形变和重力变化趋势进行了模拟(表2,图 7),这3个点的震中距分别为36km、 172km和156km。 图7b为经度方向的位移,玛多县城同震时向W运动了126mm,400a后位移量将达197mm,增加了71mm(同震效应的56%); 同震时称多和达日县城向E分别运动了8mm和19mm,400a后位移量将达39mm和43mm,分别增加了31mm(同震效应的387%)和24mm(同震效应的126%); 整体而言,玛多县城震后EW向位移量在300a后基本稳定不变,而称多和达日县城在50a后基本稳定不变。 图7c为纬度方向的位移,玛多和称多县城同震时分别向N运动了151mm和6mm,400a后位移量将达198mm和18mm,分别增加了47mm(同震效应的31%)和12mm(同震效应的200%); 同震时达日县城向S运动了22mm,400a后位移量将达67mm,增加了45mm(同震效应的204%); 玛多县城震后SN向位移量在100a后基本稳定不变,而称多和达日县城的位移量基本稳定所需时间分别为20a和100a。
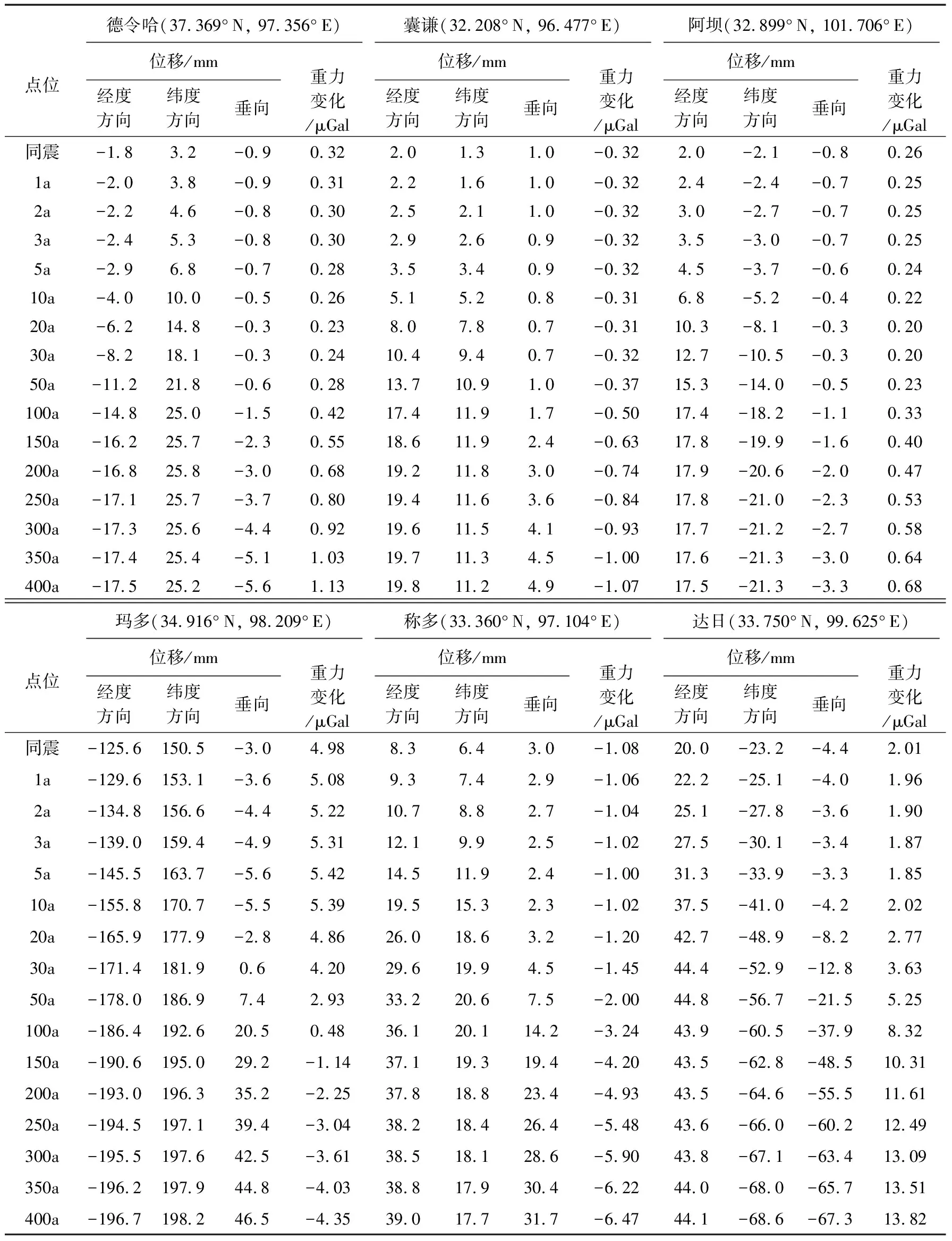
表2 部分县城位置的震后效应Table2 The post-seismic effects on some of the cities
图 7d 为垂向位移,同震时玛多县城下沉3mm,5a后累计下沉量达5.6mm,随后地表开始持续抬升,400a后抬升量将达46.5mm,400a间地表抬升量达49.5mm(同震效应的16.5倍); 称多县城在同震时地表抬升了3mm,震后5a间有微弱的下沉,随后持续抬升,400a后抬升量达31.7mm,抬升量增加了28.7mm(同震效应的9.5倍); 而达日在同震时下沉4.3mm,震后5a间有微弱的抬升,随后持续下沉,400a后下沉量达65.9mm,下沉量增加了61.6mm(同震效应的14.3倍); 3个县城震后的垂直位移量在300a后基本稳定不变。 图7e为重力变化,与垂直位移震后变化趋势类似并呈现一定的负相关性: 同震时玛多县城的重力值增加5.0μGal,5a后累计增加到5.4μGal,随后开始持续减小,400a后重力值减小为4.4μGal,400a间重力值减小了9.4μGal; 称多县城在同震时地表重力值减小了1μGal,震后5a间有微弱的增加(0.08μGal),随后持续减小,400a后重力值减小为6.5μGal,400a间重力值减小了5.5μGal; 而达日在同震时的重力值增加2.0μGal,震后5a间有微弱的减小(0.19μGal),随后持续增大,400a后重力值增大为13.5μGal,400a间重力值增大了11.5μGal; 3个县城震后地表重力变化在300a后基本稳定不变。
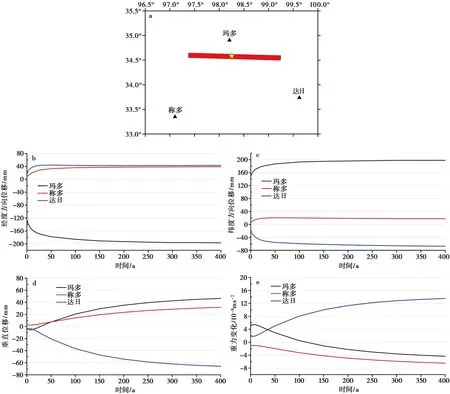
图7 震后长期时变效应Fig. 7 Long-term time-varying effects after the earthquake.a 所选点与断层的相对位置; b 经度方向位移; c 纬度方向位移; d 垂向位移; e 重力变化
5 讨论与结论
文中基于弹性-黏弹分层半空间中的矩形位错理论,采用USGS发布的由远场地震波反演的玛多MS7.4地震发震断层模型,从理论上模拟了此次地震引起的地表同震及震后形变和重力变化,通过分析可得到如下主要结论:
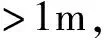
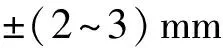
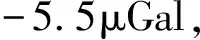

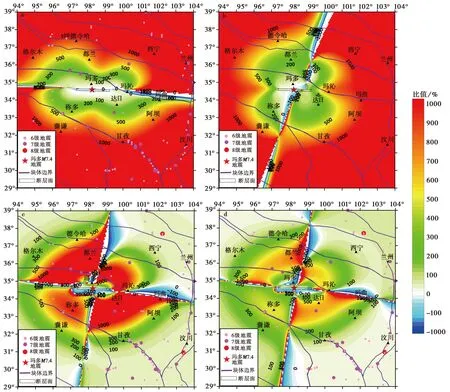
图8 震后400a间的黏弹性松弛效应与同震效应比值分布Fig. 8 The distribution of the ratios between the viscoelastic relaxation effects during 400 years after the Maduo earthquake and the coseismic effects.a 经度方向位移; b 纬度方向位移; c 垂向位移; d 重力变化


图9 震后5a间的黏弹性松弛效应与同震效应比值分布Fig. 9 The distribution of the ratios between the viscoelastic relaxation effects during 5 years after the Maduo earthquake and the coseismic effects.a 经度方向位移; b 纬度方向位移; c 垂向位移; d 重力变化
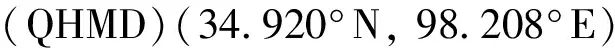
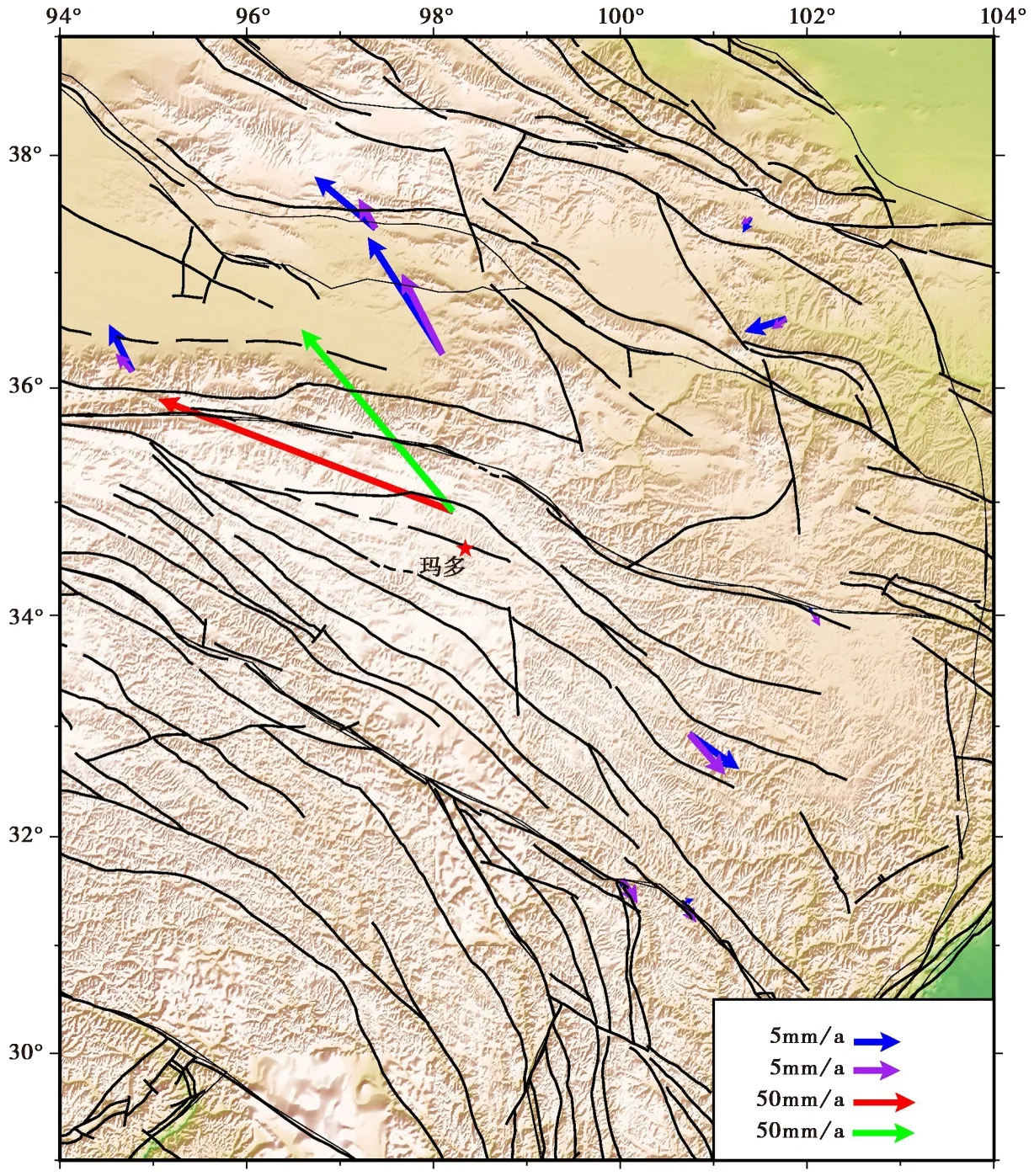
图10 同震模拟结果与GNSS观测结果的比较Fig. 10 Comparison between the coseismic simulation and GNSS observation results.蓝色和红色箭头为GNSS观测结果,紫色和绿色为模拟结果
致谢USGS提供了发震断层模型,中国地震局地震研究所赵斌博士提供了同震GNSS数据,德国波茨坦地球科学中心汪荣江教授提供了PSGRN/PSCMP程序; 审稿专家为本文提供了宝贵建议。 在此一并表示感谢!
