基于像方误差的线阵影像几何定标模型分析
2021-09-27冯世德
李 凯,冯世德*
(1.军事科学院系统工程研究院,北京 100071)
卫星成像系统精确的几何参数是遥感测绘卫星发挥应用价值、提供高精度地理信息产品的基础[1]。法国空间中心利用分布于全球的20多个检校场,将SPOT-5卫星的几何参数分为静态参数和动态参数分步检校,实现了SPOT-5卫星的高精度定位[2-3]。IKONOS卫星建设了多处检校场用于几何定标[4-5]。日本ALOS Prism卫星利用地面定标场控制点对线阵CCD进行严格内定标[6-8]。美国OrbView3影像利用影像匹配得到的密集控制点对相机内方位元素进行标定[9]。王建荣[10]等对我国天绘一号卫星的内外定标参数进行了整体标定,定标后影像无地面控制平面和高程定位精度分别达到了10.3 m 和5.7 m。孟伟灿[11]等分别对天绘卫星高分辨率影像外部和内部误差进行了补偿,补偿后影像定位精度均优于2 m。
本文首先分析了线阵推扫式相机中外部和内部定标参数对像点定位误差的影响;然后设计了不同参数的检校方法,逐个解算各定标参数的数值;最后利用多景影像对内外定标参数解算结果的可靠性与适用性进行验证。
1 线阵影像在轨几何定标模型
根据参考文献[12]、[13],星载TDI CCD推扫式相机严格几何模型可表示为:

式中,(X,Y,Z)为CGCS2000坐标系下的地面点坐标;(XGPS,YGPS,ZGPS)为CGCS2000坐标系下的相机投影中心坐标;(x,y,-f)为像点在相机坐标系下的坐标;f为相机主距;(dx,dy,dz)为卫星本体坐标系下相机投影中心与GPS相位中心的位置偏移;为相机在本体坐标系中安装角构成的旋转矩阵;为卫星本体坐标系到CGCS2000坐标系的旋转矩阵;m为比例系数。
1.1 外定标参数模型
对外部误差进行补偿的方式一般包括两种方式。
1)首先,将式(1)转化为共线条件方程,即
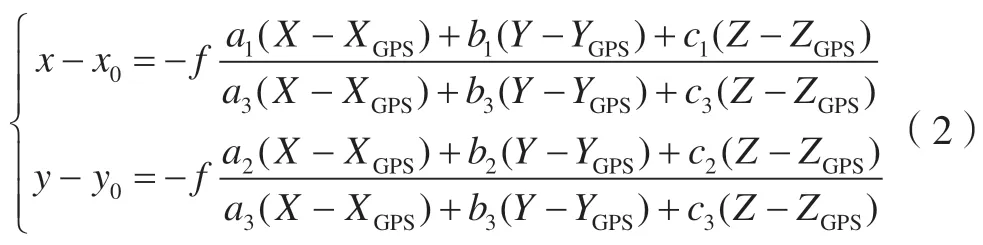
然后,分别对外方位线元素(X,Y,Z)和角元素(ω,φ,κ)(ai,bi,ci,i=1,2,3为ω,φ,κ的函数)进行建模。
2)引入偏置矩阵Roffset对外部误差统一补偿,即

式中,ω、φ、κ为X-Y-Z转角系统的3个旋转角。
3个旋转角随时间变化还存在一阶和二阶误差,因此对3个旋转角进行拓展,则有:
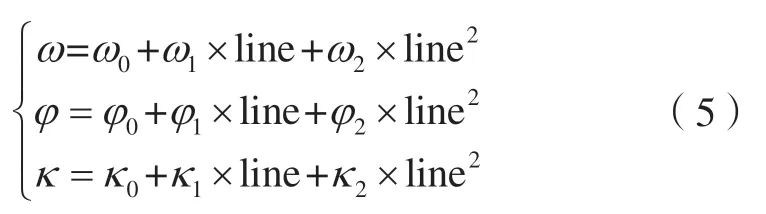
式中,line为线阵影像扫描行号,代表时间;ω0、φ0、κ0为角元素常差项;ω1、φ1、κ1为角元素一阶项;ω2、φ2、κ2为角元素二阶项。
1.2 内定标参数模型
根据相机内部误差各项参数的物理含义构建线阵影像内定标模型,即

式中,(Δx0,Δy0)为主点偏移和CCD平移;k1、k2为 镜头径向畸变系数;P1、P2为镜头偏心畸变系数;θ为CCD线阵旋转角;sy为CCD尺度变化因子;=x−x0;。
由于为常数,对式(6)进行变换得到:

式中,为各像元沿阵列方向坐标,是像元列号sample 的线性函数。
此外由于≈0,可建立线阵影像内部畸变的指向角模型,即

2 线阵影像像点定位误差分析
2.1 外定标参数对像点定位的影响
图1a中像空系的x轴指向沿轨方向,y轴指向垂轨方向,o为像主点。当外定标参数中仅存在绕沿轨方向的旋转角ω时,线阵初始位置为图1a中l,实际位置应为l'。将图1a投影至s-yz平面 (图1b)发现,ω仅造成像元列坐标的变化,变化量为dyω=cosω×y+sinω×f-y≈sinω×f。当ω中常差ω0=0、随行号(时间)变化的一阶项系数ω1=10-8时,可得到各行影像列坐标误差随行号变化如图2中实线所示;当ω中ω0=ω1=0、随行号(时间)变化的二阶项系数ω2=5×10-13时,可得到各行影像列坐标误差随行号变化如图2中虚线所示。

图1 外定标参数中仅存在绕x轴旋转角时的影响
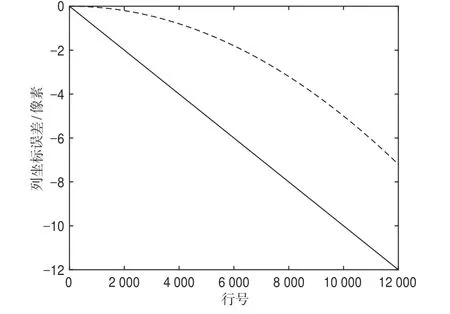
图2 ω存在一阶和二阶误差时各行影像列坐标误差 随行号变化曲线
当外定标参数中仅存在绕垂轨方向的旋转角φ时,线阵初始位置为图3a中l,实际位置应为l',可以看出,φ仅造成像元行坐标的变化,可计算得到各像元位置行坐标变化量为dxφ=sinφ×f-x=sinφ×f。当φ为φ0=2'的常差时,同一行影像上各像元行坐标误差约为1个像素。
当外定标参数中仅存在绕垂直于轨道平面的旋转角κ时,线阵初始位置为图3b中l,实际位置应为l',可以看出,κ同时造成像元行、列坐标的变化,可计算得到各像元位置行坐标误差(沿轨方向)为dxκ= -sinκ×y,列坐标误差(垂轨方向)为dxκ=-cosκ×y-y。由于κ角很小,因此dxκ≈0,可忽略不计。当κ为κ0=0、κ0=2'的常差时,可得到同一行影像上各像元行误差随列号变化的曲线如图4a所示;当κ中常差κ0=0、κ1=10-8时,可得到各行影像行中1、6 000、12 000列像元的行坐标误差随行号的变化如图4b中实线所示;当κ中κ0=κ1=0、κ2=5×10-13时,可得到各行影像中1、 6 000、12 000列像元的行坐标误差随行号的变化如 图4b中虚线所示,可以看出,当κ存在一阶误差时,同一列像点的行坐标将随行号产生线性误差,当κ存在二阶误差时,同一列像点的行坐标将随行号产生非线性误差。

图3 外定标参数中仅存在绕y轴或绕z轴旋转角时的影响

图4 κ存在常差、一阶和二阶误差时的变化曲线
2.2 内定标参数对像点定位的影响
在式(6)中x≈0,θ很小,因此内方位元素误差在沿轨方向较小;且即使θ较大,其与κ造成的沿轨误差是一致的,二者具有强相关性,在外定标参数解算时该部分误差已被改正。sy主要导致垂轨方向误差,ds=sy×y,当sy=3e-4时,可得到线阵各像元列误差随列号的变化(图5)。

图5 sy=3e-4时像元列坐标误差随列号变化曲线
3 实验结果与分析
3.1 实验数据
实验数据为3景天绘一号线阵传感器正视影像,其中第一景为定标景影像,编号为123;其余两景影像编号为124、129。124号影像与定标景影像相邻,129号影像距离定标景影像约为300 km。3景影像位于同一轨道,大小均为12 000×12 000像素,成像时间均为2012-02-21。在定标景影像成像范围内,利用Google Earth高分辨率卫星图层采集了30个控制点。由于数据来源的限制,当前尚未获得高精度的实测控制点;但从Google Earth高分辨率卫星图层中采集的控制点具有较高的定位精度,可用于解算几何定标参数,如ZHANG Y J[14]等利用Google Earth获取的控制点进行几何定标,验证了定标结果的有效性。像点坐标为手工测量,误差约为0.5~1个像元,控制点分布如图6所示。其余两景影像也采用同样方法采集了少量控制点。

图6 控制点在定标景影像上的分布
3.2 初始像方误差分析
本文计算了各控制点的初始像方误差。控制点像方沿轨残差和垂轨残差随线阵行坐标(扫描时间)的变化如图7a、7b所示;控制点像方沿轨残差和垂轨残差随线阵列坐标(像元编号)的变化如图7c、7d所示。沿轨方向和垂轨方向像点坐标的均方根误差(RMS)如表1所示。

图7 定标景影像初始像方误差
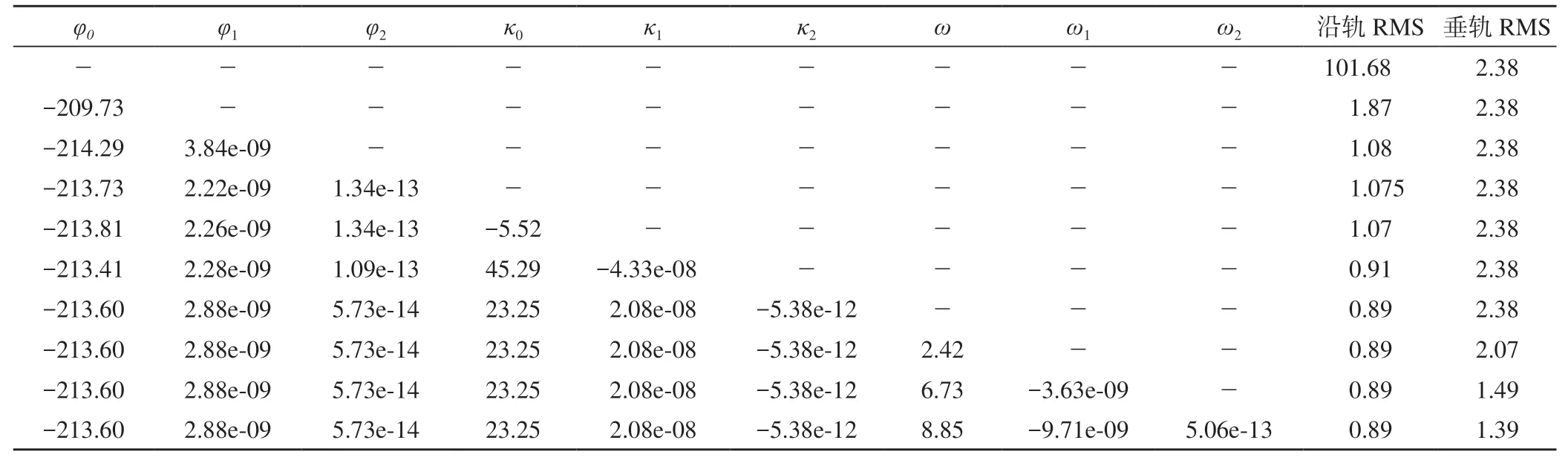
表1 对不同参数检校后参数解算值、沿轨方向和垂轨方向的RMS
根据外定标参数对像点定位的影响,可得到:
1)图7a中沿轨方向在起始时刻约有103个像素的系统残差,说明外定标参数中存在旋转角φ,且常差φ0约为2'×(-103)=-206'。
2)图7a中沿轨方向残差随行坐标变化而变化,说明参数φ存在一阶项φ1。
3)图7b中垂轨方向在起始时刻约有3个像素的系统残差,说明存在旋转角ω,且常差ω0约为2'×3=6'。
4)图7b中垂轨方向残差随行坐标变化而变化,说明参数ω中存在一阶项ω1。
根据内定标参数对像点定位的影响可知,图7d中垂轨方向残差在列坐标中间像元附近较小,偏离像元中心越远,残差越大,且残差异号,说明内定标参数存在一阶项s1。
3.3 先外后内几何定标实验
3.3.1 外定标参数解算
仅检校φ0后沿轨残差随线阵行坐标的变化如图8a所示。表1中第2行列出了检校得到的φ0的校正值以及检校后沿轨方向和垂轨方向的RMS。由图8a和表1第2行可知,检校φ0后,沿轨方向RMS精度提升效果非常明显,解算得到的φ0值与估计值也非常接近。同时对φ0和φ2进行检校,检校后沿轨方向残差随着行坐标(扫描时间)的变化如图8b所示,此时沿轨方向残差随扫描时间的变化已不明显。为了验证外定标参数φ中是否存在二阶误差,同时对φ0、φ1和φ2进行检校,检校后沿轨方向残差随着行坐标(扫描时间)的变化如图8c所示,φ0、φ1、φ2的检校值和沿轨、垂轨方向RMS列于表1第4行。

图8 对φ0、φ1、φ2检校后重新计算沿轨残差 随线阵行坐标的变化
在消除旋转角φ造成的沿轨方向像方误差后,重新给出像方沿轨残差随线阵列坐标(像元编号)的变化,如图9a所示,可以看出,在列坐标中间像元(像元编号6000)处的沿轨方向误差较小,距离中心像元越远、残差越大,说明外定标参数κ中存在常数项κ0。本文在对φ0、φ1、φ2检校的同时,分别对κ0、κ1、κ2进行逐个检校,检校结果列于表1第5~7行,对应的沿轨方向残差分布如图9b~9d所示。由表1和图9可知,单独对κ0检校时,图9b中沿轨方向残差变化很小,RMS从1.075减小至1.07,改正效果不明显;对κ0、κ1检校后,图9c中距离中心像元较远的沿轨方向残差变小,整体沿轨残差随列均匀分布,RMS也从 1.07减小至0.91,改正效果明显;对κ0、κ1、κ2检校后,图9d中沿轨方向残差变化很小,RMS从0.91减小至0.89,说明κ2对像方残差的影响很小。通过上述实验分析发现,外定标参数κ的检校中必须包含一阶 项κ1,否则难以改正κ角对像方残差的影响。另外需要注意的是,由于κ和φ之间的相关性(均造成沿轨残差),在检校κ时导致φ数值变化;同时由于κ0、κ1、κ2之间较强的相关性,在检校κ2时也将导致κ0、κ1变化。

图9 对φ、κ0、κ1、κ2分别检校后沿轨残差随线阵列坐标的变化
对φ和κ检校后,沿轨方向的系统残差已被消除。φ和κ检校前后垂轨方向的RMS如表1所示,可以看出,对φ和κ的检校均没有改变垂轨方向残差,这也验证了旋转角φ和κ主要影响像元行坐标的判断。此时,剩余垂轨方向残差仍如图7b所示,其中系统残差主要是由旋转角ω造成的。分别对ω0、ω1、ω2进行检校,结果列于表1的第8~10行,可以看出,对ω角中常数项ω0和一阶项ω1检校后,垂轨方向RMS明显减小,说明ω角中存在较大的常差和一阶项。ω角检校完成后,垂轨方向残差减小至1.39个像素,垂轨残差随线阵行坐标的变化如图10a所示,可以看出,对ω角改正后垂轨方向系统残差已被消除,垂轨残差随扫描行的变化均匀分布;但垂轨残差的数值仍较大,这主要是由内定标参数误差造成的。垂轨残差随像元列坐标的变化如图10b所示,可以看出,垂轨方向残差与图7d非常类似,且随列坐标的变化规律更加明显,因此下一步需要求解内定标参数标定,以消除垂轨系统残差。
3.3.2 内定标参数解算
根据内定标参数对像点定位的影响、对图7d中垂轨方向残差的分析以及图10b中垂轨残差随像元列坐标的变化可知,内定标参数中应主要包括主点偏移、CCD尺度变化因子以及CCD排列旋转角误差。因此,本文在对外定标参数检校后,首先检校与这些误差相关的参数,即式(8)中的l0、l1、s0和s1。内定标参数解算结果与沿轨、垂轨RMS列于表2第1行,可以看出,对主点偏移、CCD尺度变化因子以及CCD排列旋转角误差标定后,沿轨残差和垂轨残差均进一步减小,其中垂轨方向RMS由1.39减小至0.89,效果明显。然后,对式(8)中所有内定标参数进行检校,结果列于表2第2行,可以看出,沿轨方向RMS已不再变化,垂轨方向RMS由0.89减小至0.81,说明CCD尺度变化因子是内定标参数中影响定位结果最主要的因素。垂轨残差随列坐标的变化如图11所示。对比 图11和图10b可知,内定标参数检校后,垂轨方向残差明显减小,且残差随像元列坐标均匀分布,系统性残差被消除。
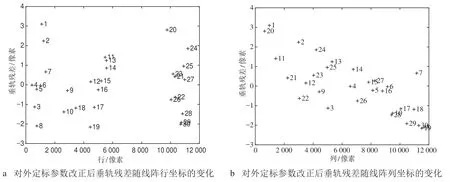
图10 对外定标参数改正后垂轨残差随线阵行、列坐标的变化

图11 所有内、外定标参数检校后垂轨残差随列坐标的变化

表2 内定标参数检校后参数解算值、沿轨方向和垂轨方向的RMS
3.4 定标参数适用性验证
本文利用定标景影像和定标景轨道上其他影像进行定位实验验证。应用定标景影像内外定标参数前后该景影像检查点的像方定位结果如表3所示,可以看出,利用内定标参数重新定位后,定标景影像垂轨方向残差明显减小;利用解算得到的内外定标参数再次对检查点进行定位,沿轨和垂轨方向的RMS均减小至1个像素左右;利用外定标参数重新定位后,沿轨方向和垂轨方向RMS均得到了有效改善,验证了本文定标参数的有效性。

表3 应用于定标景影像实验的内、外定标参数/像素
将内定标参数应用于124号和129号影像,并利用少量控制点对外部误差补偿,再进行像方定位实验,定位结果如表4所示,可以看出,124号和129号影像直接定位误差均较大,且随着时间的推移,垂轨方向RMS有变大的趋势;利用内定标参数重新定位后,这两景影像垂轨方向RMS均减小了约0.4~0.5个 像素,说明内定标参数是有效的,也验证了航天相机内部几何结构是稳定的;利用少量控制点对两景影像进行外部误差补偿后,取得了与定标景影像相当的定位精度,说明内定标参数已基本补偿了内部 误差。
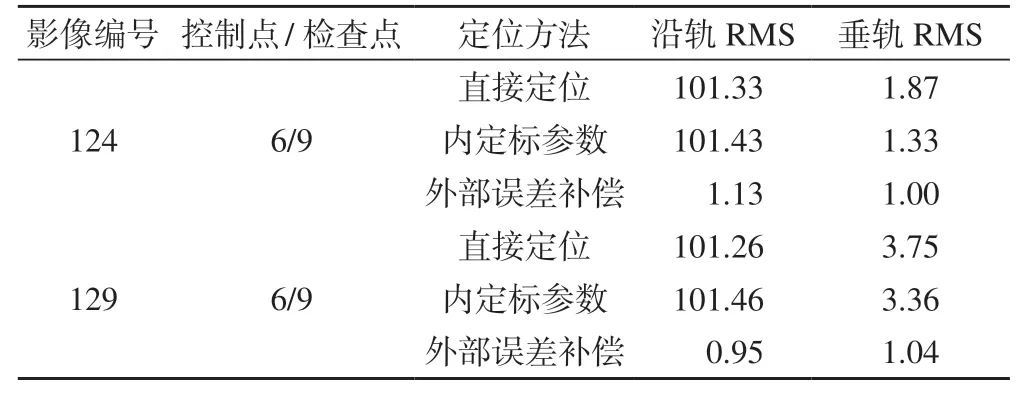
表4 应用于其他景影像实验的内定标参数/像素
4 结 语
本文基于像方误差对内外定标参数进行了分析,在此基础上构建并验证了线阵影像定标模型。将计算得到的内、外定标参数应用于定标景影像检查点取得了较好的定位结果;将内定标参数应用于其他景影像时,达到了与定标景影像相当的定位精度。验证实验表明,本文采用的定标模型可计算出有效的内、外定标参数,同时验证了航天摄影测量相机内部几何结构的稳定性。
