如何提升高中数学习题课教学效率
2021-09-27李玉莲
李玉莲
(江苏省泰兴中学 225400)
随着新课程改革全面实施,各个学科在此背景下也相继做出改革和创新,数学作为贯穿学生整个学习生涯的重要课程,自然而然需要引入全新的教学理念和教学方式.其中习题课在锻炼学生思维能力方面发挥着不可小觑的作用,通过讲解和点评习题能让学生巩固所学基础知识,健全完善知识系统,提升学习能力.故而,教师可从多方面优化数学习题课教学,实现预期课程目标.
一、借助变式习题教学,培养运算能力
想要提高学生运算能力,必不可少的是学生解题技巧和策略的掌握,提高学生的解题思维.解题技巧是学生数学学习和解题中采取的方法,是一种更为简单的解题方法.在数学教学中,常用的有数形结合方法、转化思想等,解题策略主要是问题解决采用的方式,如切割法、补形法等,面对数学问题需要准确找到解题方法和思路,完成数学问题的解答,提高习题课教学效率和质量,帮助学生形成良好的解题思维,提高学生问题分析和解决的能力,促进学生学习能力进一步提升.在具体的习题教学中,教师可以利用变式习题、一题多解习题等,灵活利用不同的技巧和策略,针对同一个问题或者定理,让学生从不同的角度进行思考,引导学生分辨和判断,掌握不同的解题方式,并且能够灵活利用其解题.
例1x∈R,不等式(m-1)x2+(m-1)x+2>0恒成立,求解m的取值范围.
变式1如果不等式x2+mx+2>0在x∈[1,2]上恒成立,求解m的取值范围.
变式2如果不等式x2+mx+2<0在x∈[1,2]上恒成立,求解m的取值范围.
变式3如果不等式x2+mx+2>0在m∈[1,2]上恒成立,求解x的取值范围.
例2已知数列{an}是等差数列,S10=100,S100=10,求解S110的值.
在此题解答时,可以有好几种解题方式.
方法1常规方法(利用方程思想解题)

方法2待定系数法(函数思想)
根据等差数列{an}的前n项和公式,设Sn=An2+Bn,根据已知列出算式,求解出A和B的值,S110=A×1102+B×110,计算得出答案为-110.
方法3利用性质
因为数列{an}是等差数列,所以S100-S10=a11+a12+…+a100=-90,因为a1+a110=a11+a100=-2,所以得出S110=-110.
在高中数学变式习题教学中,借助变式习题和一题多解习题,解放学生思想,培养学生数学思维,优化习题教学设计,实现学生学习能力的培养和提升.
二、利用探究性习题教学,提高合作学习能力
高中数学中的知识内容比较多,并且知识较为抽象,学习难度比较大,对学生逻辑思维能力要求较高.在具体的教学中,应当将抽象和复杂的知识简单化,帮助学生学习和掌握.小组合作学习引入高中数学解题教学中,有利于学生数学思维培养,加深数学知识的理解和掌握.作为高中数学教师,应当结合教学内容,优化课堂教学设计,对知识内容进行细化分析,明确课堂教学目标,保证教学目标的可行性和针对性.例如,在高中数学“不等式最值求解”的教学中,利用基本不等式求解最值是高考中常见的题目,也是高考中的热点题目,有利于学生数学思维培养.在基本不等式中,题目类型比较多,要根据不同类型进行题目解答.
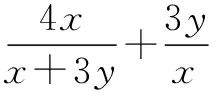
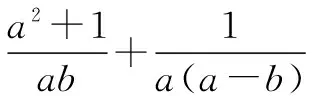
例5当0 在展示题目之后,组织学生开展合作学习,结合学生解题,让学生总结此类题目解题方法.在合作学习过程中,教师可以适当指导学生,让学生掌握构造定值的方式.在合作学习中,学生之间的互动与交流,能够促进学生思维碰撞,让学生利用不同数学方法解题,培养学生思维能力,激发学生自主学习和探究欲望. 在新课程改革背景下,注重学生核心素养培养,数学建模是重要的内容,从字面来说,就是构建模型,根据实际的数学问题,构建相应的数学模型,帮助学生理解和解答问题,提高学生解题效果.在高中数学解题中,有效利用数学模型,借助数形结合等方式,有效解答数学问题,可锻炼学生解题能力.高中数学抛物线的学习中,抛物线主要是由二次函数和一元二次方程转化而成的,在研究中,主要研究图像性质,如增减性、奇偶性等,对于函数来说,学生并不陌生,如一次函数、反比例函数、二次函数等,借助这样的类比学习,引入数形结合思想,可帮助学生学习和掌握.同时,教师可以利用多媒体展示抛物线图象,以及二次函数在生活中的应用,如拱形桥、篮球投篮等等,这些是生活中常见的抛物线,之后设计相应的问题,已知拱桥的宽度,求解拱桥顶点坐标.在这样的解题中,学生会自然而然构建直角坐标系,找出相应的参考点,求出点的坐标.在这样的数学模型构建中,强化学生数学建模能力,内化数学知识,理解数学知识本质,提高学生建模能力,进一步提升学生核心素养. 高中数学和小学、初中两个阶段相比,无论知识容量和难度均有所增大,学生在学习过程中倍感吃力.再加上当前很多数学教师采取的方式过于一刀切,未充分考虑不同层次学生的学习情况,导致数学基础和水平较差的学生则无法紧跟教师教学步骤,逐渐成为学困生.再加上部分数学成绩优异的学生因能高效理解教师传授的知识内容,不可避免的会出现松懈和自负心理,因此这种教学方式也不利于提升学生学习成绩.分层教学模式能有效改变上述教学现状,即教师结合不同学生学情实施针对性较强的教学方式,保证每位学生均能在数学课堂中有所收获,提升学习效率和学习数学的自信心.例如在学习等比数列习题时,教师首先根据学生数学学习的综合表现将学生分成A、B、C三个层次,制定本课教学目标时也根据不同层次水平的学生一一确立.比如,A类学生理解能力较强,则要求他们在理解这一公式的基础上掌握错位相减法求和、倒序求和等技能技巧;B类学生理解能力中等且基础较好,则要求他们在掌握教材中公式的推导过程之外了解另外两种推导公式的方法;C类学生是数学学习中能力较低的学生,则要求他们了解并记忆教材中对这一公式的推导过程.同时,教师还可以精心准备一些基础训练题以促进学生对这一公式的应用、巩固与掌握. 例7过双曲线2x2-y2=2的右焦点做直线L,和双曲线的交点是A、B.如果|AB|=4,则有几条这样的直线. 在学生解题之后,让学生讨论曲线中过焦点的线段|AB|是否是最短的,让学生在课后进行推理,思考焦半径什么情况下最短.在这样的讨论中,考虑学生个性差异的同时,注重学生主体作用的发挥,让学生开展自主学习和探究,提高学生学习效果. 总之,习题课作为数学学科不可缺少的组成,教师应改变传统教学的思想观念,细心指导学生分析习题,使学生掌握高效解题技巧,提高自主探究和学习能力,达到充分锻炼数学思维的目的.与此同时,数学教师需为学生营造愉悦、舒适的课堂氛围,引导学生在活而不乱的课堂环境中调动知识和思维,提升习题课的效率和质量.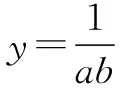
三、利用综合性习题教学,提高模型构建能力
四、注重个体差异,发挥学生主体作用
