基于人口流动和时空信息的城市疫情影响研究

张恺悦，詹秀秀，张子柯

(阿里巴巴复杂科学研究中心，杭州师范大学阿里巴巴商学院，浙江 杭州 311121)

2019年底，新型冠状病毒肺炎(下文简称COVID-19)疫情在武汉暴发.疫情暴发时，正值春运期间，导致疫情在短时间内大范围传播.2020年3月11日，世界卫生组织(WHO)正式宣布，将2019新型冠状病毒疫情从流行病升级为全球大流行病.截至2020年10月12日，国内累计确诊病例为91,352例，世界范围内累计确诊病例为37,718,489例[1].这场全球公共卫生危机，给社会治理、生活和经济等诸多方面带来了深刻影响.为了控制疫情的发展，在疫情暴发后，国家采取了最全面最严格最彻底的防控措施，全国人民按照专家建议居家隔离，才使得疫情快速得到控制.

从疫情开始以来，大量研究人员对COVID-19进行了研究，这些研究主要集中于医学方面[2-3]和疫情预测分析方面.在对疫情进行预测分析时主要使用大数据、传播动力学模型[4-10]和统计计算学习[11-15]等方法.文献[4] 基于SIR模型和COVID-19疫情发展呈现的演化趋势对疫情进行了建模及预测.该研究表明疫情在2020年2月9日左右达到峰值随后确诊人数将会下降.文献[5] 基于SEIR模型，假设2020年1月25日前出现的确诊病例是疾病在没有干预的情况下自由传播导致的.进一步地，该研究使用《人民日报》对全国2019例新型冠状病毒感染病例的实时报道，得出基本再生数在2.8～3.3之间.文献[11] 基于安徽省卫生健康委员会公布的病例信息，构建了全国除湖北外各省疫情传播的自回归模型，有效刻画了疫情发展中后期的演化规律，为理解疫情传播后期的内在机制提供帮助，为疫情防控决策提供参考.文献[12] 使用数学建模和回归模型对国内疫情的拐点进行了预测，发现中国和世界范围的COVID-19疫情数据均遵循三次函数，而除湖北外的全国疫情数据符合二次函数分布.预测国内疫情的拐点在2020年2月9日.张琳[13]使用非线性函数拟合国内的疫情情况，发现确诊人数在经历了初期的无障碍指数增长，中期的次指数增长后，已进入了次线性增长阶段.上述的研究都是基于疾病本身的演化趋势对疾病进行分析、建模以及预测.然而，很多其他外在因素会对疾病的传播存在影响.比如说，新型冠状病毒主要通过直接传播、气溶胶传播和接触传播，所以大规模人口流动是导致疫情迅速扩散的一个重要因素[16-19]，地理位置也在很大程度上影响了各地区之间的疫情传播[20-22].这也从理论上说明了只有武汉封城才能有效遏制疫情的传播[23-25].文献[9] 提出了一个基于数据驱动的人口模型，该模型利用人口的实际流动来衡量中国在疫情暴发早期限制出行对于疾病传播的影响.该文章研究表明，真实的人口流动数据是理解疾病传播的一个关键因素.文献[10] 基于SEIR传播模型分析模拟了中国的疫情发展.该文章使用马尔可夫链蒙特卡洛方法估计疾病流行的基本再生数在2.47～2.86之间.为了考虑武汉及周边城市防疫政策影响，该文章使用中国大陆300多个地级市的人口流动数据，预测出武汉的累积确诊人数将会达到75,815人.此外，除了COVID-19之外，文献[26] 对巴基斯坦登革热的传播与人口迁徙之间的关系进行分析研究，发现传染病的传播是与人口迁徙有关的.

然而，上述研究并没有系统针对疾病数据与迁移数据进行具体的相关性分析.本文首先基于城市的疾病感染数据和迁移数据，对两者进行了细致地相关性分析，发现城市的疾病确诊人数与该城市迁出指数高的城市的确诊人数存在强相关性.并且，距离武汉(即疾病重灾区)较近的城市确诊人数偏多.基于以上的分析，本文将上述与疾病存在强相关性的变量作为特征，利用机器学习算法，即线性回归和随机森林，对未来疾病的确诊人数进行预测.并且对比了两种机器学习的方法对疾病预测的有效性，进一步分析了哪些因素对于疾病预测更重要.

1 数据分析

1.1 数据描述

疾病数据我们收集了2020年1月24日到2020年3月9日，中国大陆COVID-19疾病相关数据.疾病数据来源于国家卫生健康委员会[1]，我们只考虑有感染病例的322个中国大陆地级市的每日确诊人数.

图1 疾病数据可视化Fig.1 Visualization of the disease data

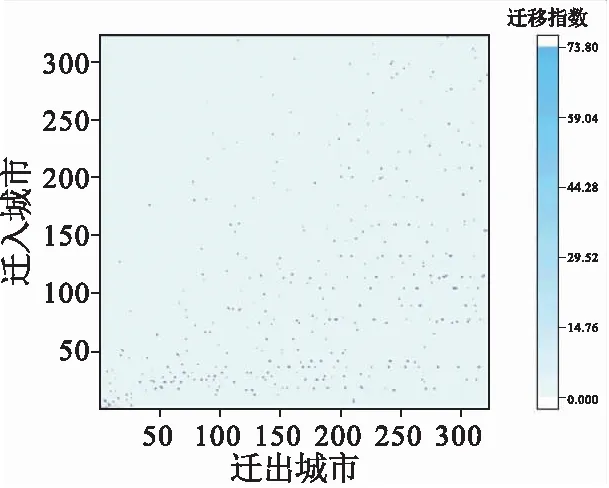
图2 城市迁出与累计感染人数的关系Fig.2 Relationship between city-level population migration and the number of confirmed cases

人口迁移数据我们通过百度迁徙收集了中国大陆322个地级市之间的人口迁入和迁出指数(1)迁出指数：是目标城市迁出到被迁入城市的人口规模占目标城市当日所有迁出人口规模的百分比，反映迁出人口规模，城市间可横向对比；，共收集了2020年1月24日到2020年3月9日44 d的数据.图2中显示了各地级市之间迁出指数的可视化.

图2中我们将城市按照累计确诊人数从大到小依次排序给定索引，即城市感染人数越多，该城市的索引值越小.例如武汉的累计确诊人数最多，它的索引值为1.图中颜色表示每个城市(x轴)迁出到其他城市的迁移指数(y轴).

1.2 疾病与迁移数据相关性分析

人口的移动可能会对疾病产生影响[11].例如，一个没有感染病例的地区，可能因为感染人口的迁入导致疾病的暴发.在图2中我们给出了城市的确诊病例数与该城市的迁移指数的关系.图中x轴表示迁出城市，y轴表示迁入城市，图中颜色越深表示迁移指数越高.坐标轴上的城市均按照各城市累计确诊人数降序排列(即，1代表累积确诊人数最多的城市，322表示累积确诊人数最少的城市.图中的每一个坐标点(x,y)表示城市x到城市y的迁出指数.例如，(1,322) 表示城市1到城市322的迁出指数).从图2中可以看出，疫情严重的城市到疫情严重的城市的迁出指数相对比较高，而疫情不严重的城市到各个城市的迁出指数比较平均.

由图2可以看出疫情严重的城市之间迁移更频繁，因此我们对迁移指数与确诊人数之间的相关性进行了定量分析.图3分别展示了各地级市(下文简称‘市’)确诊人数和以下变量的相关性，即(i) 武汉到目标城市之间的迁出指数；(ii) 目标城市迁出指数最大的城市的确诊人数；(iii) 武汉到目标城市的距离以及(iv) 离目标城市最近的城市的确诊人数.我们在图中列出了各变量之间双对数坐标下的皮尔逊相关系数(PCC).从图3(a)中可以看出，武汉到相应城市之间的迁出指数(x轴)与确诊病例数(y轴)的PCC为R=0.84，也就是说确诊病例数与迁出指数之间成正比，即武汉迁出到该市的比例越高，确诊病例就越多.进一步的，我们研究了城市确诊人数与目标城市最大迁出城市的确诊人数之间的相关性.如图3(b)所示，各城市确诊人数与目标城市最大迁出城市的确诊人数之间表现出较强的线性相关性(PCC为R=0.84)，即一个城市最大迁出城市的疫情越严重，该城市的疫情就会越严重.与迁移数据相似，图3(c)展示了武汉到相应城市的距离(x轴)与各城市确诊人数(y轴)的相关性.确诊病例数与武汉到相应城市的距离之间的PCC为R=-0.67，呈现非常强的负相关性.这说明离武汉越远的城市，确诊病例数就越少，反之亦然.并且，各城市确诊人数与目标城市最近城市的确诊人数之间的PCC为R=0.49，即一个城市最近城市的确诊人数和该城市的确诊人数之间成正比，即一个市最邻近的城市的确诊人数越高，该市的疫情就越严重.综上所述，武汉到相应城市的距离与迁出指数都与COVID-19的确诊人数有较强的相关性.

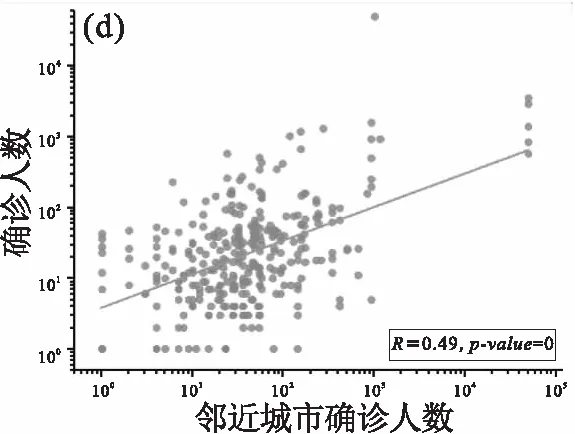
图3 各城市每日累积确诊人数与各种影响因素之间的皮尔逊相关性分析Fig.3 Pearson correlation between city-level daily cumulative number of confirmed infected cases and various factors

2 疾病预测模型

针对上述各城市的确诊人数与距离，迁移指数之间的相关性.我们拟使用这些与确诊病例数存在强相关性的变量作为特征，对疾病进行预测.我们以线性回归和随机森林为学习模型，具体的模型介绍如下.

2.1 线性回归

(1)

其中，n是训练样本的数目，m是每个特征xi的维数，βi是要学习的回归参数.

2.2 随机森林

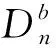
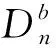
进行预测时，对测试集的预测结果，是由对所有决策树得到的结果取平均值得到的.放回取样方法可以在不增加偏差的情况下减小模型的方差，从而获得更好的预测性能.

3 预测结果及分析

根据上文对确诊人数与各因素之间关系的分析，本节将研究这些因素在传染病发展情况进行预测时起到的作用.本文使用线性回归和随机森林算法作为预测模型，预测时使用的特征为从疾病、迁移信息以及上文中提到的其他信息.

在预测时，本文对原始数据进行了处理.由于在2020年1月25日之前只有118个城市有感染病例，而大部分城市没有感染者.因此，本文采用了从2020年1月25日到2020年3月9日有新增确诊病人的322个城市，一共45 d的数据.我们使用前35 d的数据作为训练集，剩下的10 d数据作为测试集.为了对比人口迁移数据及其他数据在预测中起到的作用，本文使用仅用本城市历史疾病数据进行预测的模型作为基准模型.

在这一节，我们首先介绍预测性能的评价指标.然后，介绍以本城市历史疾病数据进行预测的基准模型的预测结果.进一步地，我们将人口迁移的数据以及其他数据加入到基准模型中，以探讨这些信息对预测结果的影响.

3.1 性能评价指标

(2)

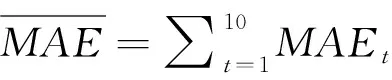
3.2 基于目标城市历史疾病数据进行预测

图4 基于目标城市的历史疾病数据的预测结果Fig.4 The prediction performance based on the target city’s historical disease data

3.3 基于历史疾病及迁出指数的预测

其中M1(*)和M2(*)分别表示目标城市迁出指数最大的城市以及目标城市迁出指数第二大城市的特征，以此类推.

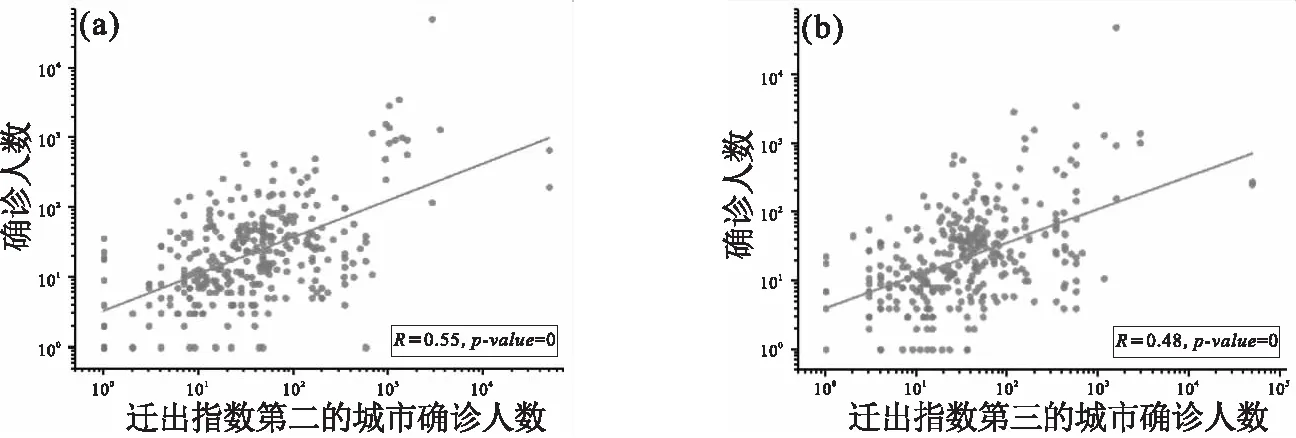
图6 各城市每日累积确诊人数与到目标城市迁出指数较高城市的每日确诊人数之间皮尔逊相关性分析Fig.6 Pearson correlation analysis between the number of daily confirmed cases in each city and the number of daily confirmed cases in the city with a higher migration index to the target city

图7 基于目标城市及与目标城市迁出指数较大的城市历史疾病数据的预测Fig.7 The prediction performance based on the historical disease data of the target city and the cities have large migration index with target city

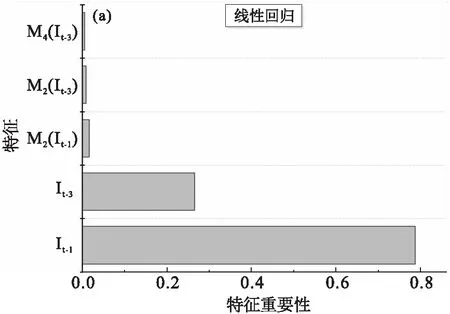
加入目标城市迁出指数较大的城市的历史疾病数据作为特征，预测效果提升了10%以上，说明迁移相关特征的加入可以帮助预测.为了具体了解各个特征在预测中的作用，我们计算了两个算法在n=4,q=5时各个特征的重要性.图8展示了两个算法最重要的5个特征，可以看出，本城市的历史疾病数据，特别是前1天的确诊人数，在预测中起到主导作用.然而，除本城市确诊人数特征外，目标城市迁出指数较大的城市确诊人数特征也起到了比较重要的作用.

3.4 基于目标城市及其邻近城市历史疾病数据的预测

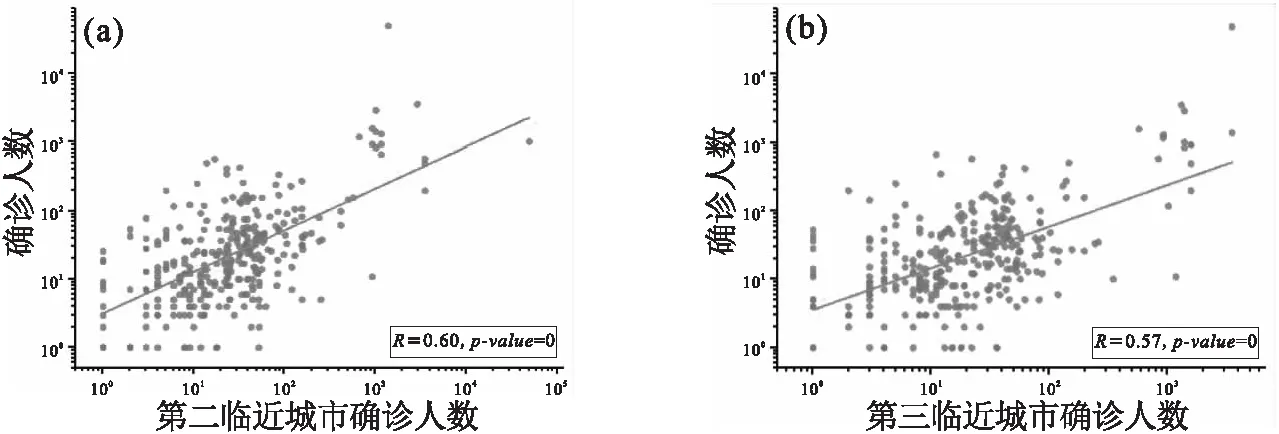
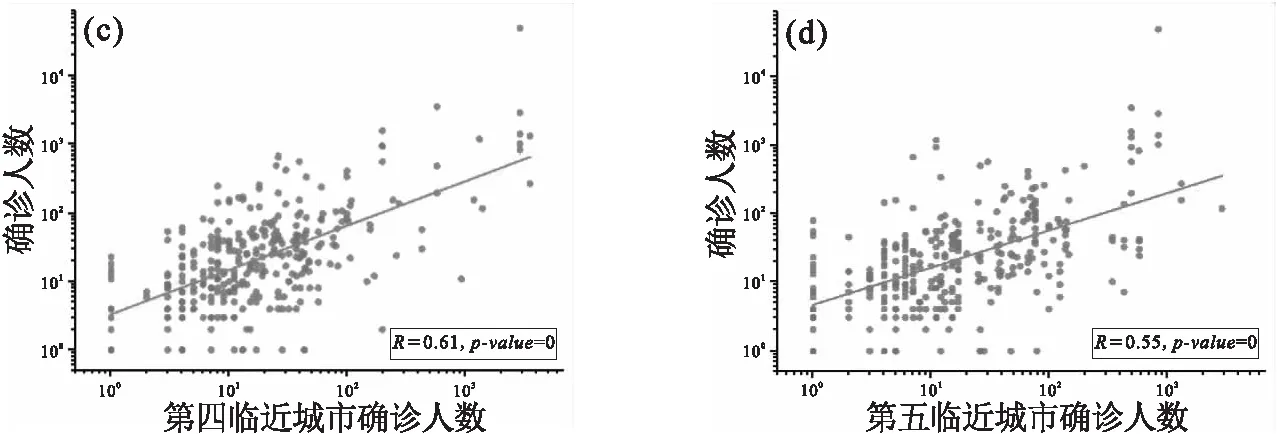
图9 各城市每日累积确诊人数与距离目标城市距离较近城市的确诊人数之间皮尔逊相关性分析Fig.9 Pearson correlation analysis between the number of daily confirmed cases in each city and the number of daily confirmed cases in the neighboring cities of target city

图10 基于目标城市及临近城市的历史疾病数据进行预测 Fig.10 The prediction performance based on the historical disease data of the target city and the neighboring cities of the target city

加入目标城市邻近城市历史疾病数据作为特征，预测效果提升了10%以上，说明该特征的加入可以帮助预测，且效果优于加入目标城市迁出指数较大的城市的历史疾病数据作为特征.为了具体了解各个特征在预测中的作用，我们计算了两个算法在m=5，n=4时各个特征的重要性.

图11展示了两个算法最重要的5个特征，可以看出，本城市的历史疾病数据，特别是前一天的确诊人数，在预测中起到了主导作用.然而，除本城市确诊人数特征外，目标城市邻近城市的确诊人数特征在预测中也起到了比较重要的作用.

综上所述，随机森林的预测效果总体上优于线性回归.3种模型中，基于目标城市及其邻近城市历史疾病数据的模型预测效果更好，但两种模型的预测效果都比基础模型好，如图12所示.由此可见，添加邻近城市历史疾病数据或迁出指数较大的城市历史疾病数据，可以使预测效果变好.

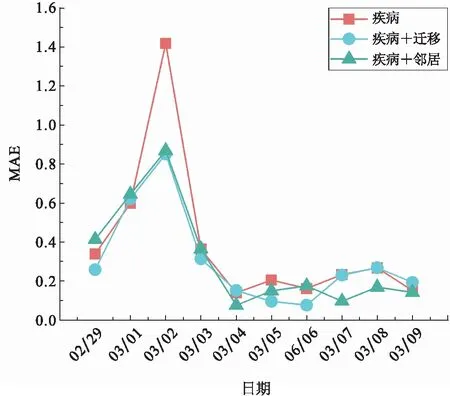
图12 3种模型预测效果最好时的10 d MAEFig.12 The best MAE of the three different models

4 结论

本文分析了各城市确诊人数和以下变量的相关性，即(i)武汉到相应城市的距离；(ii)武汉到目标城市之间的迁出指数；(iii) 离目标城市最近的城市的确诊人数以及(iv)目标城市迁出指数最大城市的确诊人数.发现各城市确诊人数与上述各因素之间均存在较强的相关性.根据相关性分析的结果，本文进一步使用线性回归和随机森林算法作为预测模型，预测时使用的特征为从疾病、迁移信息以及位置信息中提取的特征.迁移信息相关特征和位置信息相关特征的加入使得预测效果有较大的提升，对比两种特征来说，添加位置信息相关特征，对预测效果的提升更显著.