复杂障碍物环境下基于转向约束的智能汽车路径规划方法研究
2021-09-27陈佳佳
姜 康,王 皓,陈佳佳
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
0 引 言
智能车辆研究的关键问题有:定位、感知、规划、决策以及控制。路径规划是规划的重要一环,在机器人领域又称为运动规划,是指用于将期望的运动任务分解成离散的运动,以满足运动的限制,并可能优化运动的某些方面。智能车中的路径规划,是指生成一条从起点到终点的可行驶路径,同时满足时间、环境以及车辆动力学等约束[1]。
智能汽车可理解为一种多轮机器人,因此智能车路径规划算法与机器人领域相关算法一脉相承。常见有模糊规则法、遗传算法、神经网络、蚁群优化算法等,但这些算法的复杂度会随着自由度增加呈指数级增长,并不适合解决复杂障碍物下的规划问题。此外还有基于图的算法例如A*算法[2]、D*算法、人工势场法[3,14]等,这类算法虽满足路径规划的实时性和最优性要求,但规划的路径并未考虑车辆的动力学特性,使规划路径不一定符合智能汽车的运动约束。
基于采样空间的算法,搜索速度快且算法复杂度不会随着自由度的增加转向指数级增长,比较适合智能车的规划问题。快速随机搜索树(rapidly-exploring random tree,RRT)作为此类算法的代表[4],由LAVALLE提出,但是此算法存在3点缺陷:①在全局使用均匀采样,虽保证了算法的概率完备性,却导致算法的开销过大,降低了收敛速度;②原始的最邻近算法在存在复杂约束时算法可能多次失效,因而无法满足实时性要求;③在全局的随机采样,导致生成路径不平滑,无法满足智能车的动力学约束。针对以上几点不足,国内外的研究学者做出了一些改进。为了加快算法的收敛和搜索效率,S.M.LAVALLE提出了Bi-RRT[5]和 Goal-biasing RRT算法[6];为了降低不准确的度量距离对RRT探索能力的影响,A.SHKOLNIK等[7]提出了RG-RRT(Reachability guided RRT)算法;由于随着RRT算法采样点趋向于无穷,收敛到最优解可能性趋于0; S. KARAMAN等[8]提出了渐进最优(Asymptotic optimality)的RRT*算法,但会导致算法的开销变得十分庞大;为解决由于RRT算法的随机采样所导致的生成路径不平滑问题,T.FRAICHARD等[9]采用了回旋曲线进行平滑处理,但由于回旋曲线没有闭合形式解,无法满足实时性的要求;B.LAU等[10]采用了5次贝塞尔曲线,但未考虑生成路径的曲率连续性,因此无法满足智能车的动力学约束;此外还有利用深度学习[11-12]训练高回报点从而优化路径,但可靠性和可解释性还不是很高。
针对以上各类RRT衍生算法的不足,笔者就复杂障碍物环境下的智能汽车的路径规划问题,提出了一种基于改进的Bi-RRT算法。利用车辆的转向约束进一步缩小采样空间,结合Bi-RRT的快速搜索性使得路径的生成更加迅速。并通过仿真实验,验证了该算法的有效性、实用性和适应性。
1 车辆运动学模型
针对机器人的传统规划算法均未考虑车辆的动力学模型,而对于智能汽车来说,车辆自身的动力学限制尤其重要,否则即使规划好了路径,车辆也不一定能跟随预定生成的轨迹。采用常见的阿克曼转向模型作为动力学模型,如图1。

图1 车辆动力学模型Fig. 1 Vehicle dynamics model
该模型具有三个自由度,(x,y)表示车辆在系统坐标系下的位置,θ代表车辆纵轴轴线与坐标系之间的夹角,φ为前轮转角。假设车辆的速度为v,R为转向半径,k为转向曲率,那么在任何运动瞬间,车辆满足式(1):
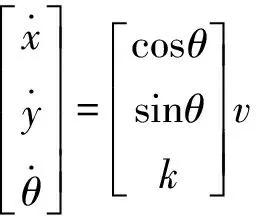
(1)
车辆模型受到动力学约束,故需要满足式(2):
(2)
式中:vmax为最大车速;φmax为最大前轮转角;Kmax为最大转弯曲率;Rmin为最小转弯半径。
2 改进的RRT算法
2.1 基本的RRT及Bi-RRT算法
基本的RRT算法是一种基于采样的单查询增量式树状结构算法。初始化时随机树T只包含一个初始节点qstart,随后在状态空间里随机的选择节点qrand,再遍历T树,找出距离最近的节点qnear,最后扩展函数从qnear向qrand扩展一段距离,生成一个新的节点qnew。随后检查新节点qnew是否与障碍物发生碰撞,若是则扩展函数返回空,放弃此次生成的qnew;否则将qnew添加至T树。按照以上步骤反复迭代,直到新的节点qnear与目标点qgoal的距离小于一定的阈值,则代表T树到达了目标点算法成功。若算法达到了最大循环次数依旧未能达到设定阈值,则算法失败。最后,由目标点qgoal回溯到初始节点qstart,得到算法所规划出的路径。算法如图2,具体搜索示意过程如图3。

图2 基本RRT算法Fig. 2 Basic RRT algorithm

图3 基本的RRT算法示意Fig. 3 Schematic diagram of the basic RRT algorithm
双向RRT算法的基本思想是在基本RRT上,从初始点和目标点同时构建随机搜索树。需要注意的是,第二棵树的扩展方式与基本RRT算法的扩展方式略有不同,它会以第一棵树生成的qnew代替qrand进行扩展,算法结束的标志即是两棵树相连。此外,考虑到两棵树的平衡性(即两棵树的节点数的多少),需要交换次序选择“小”的那棵树进行扩展,使Bi-RRT算法较基本RRT算法更加有效。Bi-RRT搜索过程如图4。基本的Bi-RRT算法示意如图5。

图4 基本Bi-RRT算法Fig. 4 Basic Bi-RRT algorithm

图5 基本的Bi-RRT算法示意Fig. 5 Schematic diagram of the basic Bi-RRT algorithm
2.2 改进的Bi-RRT算法流程
通过对智能车规划问题的分析及对基本RRT算法的介绍,笔者提出了一种在复杂障碍物环境下基于Bi-RRT改进的智能车规划算法。具体算法步骤如图6。算法的主要改进有两点:①通过车辆的转向约束限制了采样空间,可以避免在整个采样空间进行搜索,加快了算法的收敛速度;②在节点生成时,根据转向约束限制节点的生成,使得生成的路径更加符合车辆的动力学约束。具体改进的算法详见2.3、2.4节。

图6 改进的Bi-RRT算法Fig. 6 Improved Bi-RRT algorithm
2.3 基于转向约束的概率目标偏向采样策略
基本的RRT以及基本的Bi-RRT在随机采样的过程中,都是在全局范围内的随机搜索,这样会导致有很多无谓的搜索而浪费计算资源,也使得路径的生成更加缓慢。针对这一问题,笔者采在随机树每次的生长过程中,基于转向约束限制采样空间,从而避免了很多不必要的搜索,如图7。由图7可知,对于整个T树而言,寻找最邻近点时不必搜索全树,而是考虑车辆自身转向约束,先在生成的子树中确定车辆允许的转向区域,再从相应区域内寻找最近点。

图7 基于转向约束的搜索Fig. 7 Search based on steering constraints
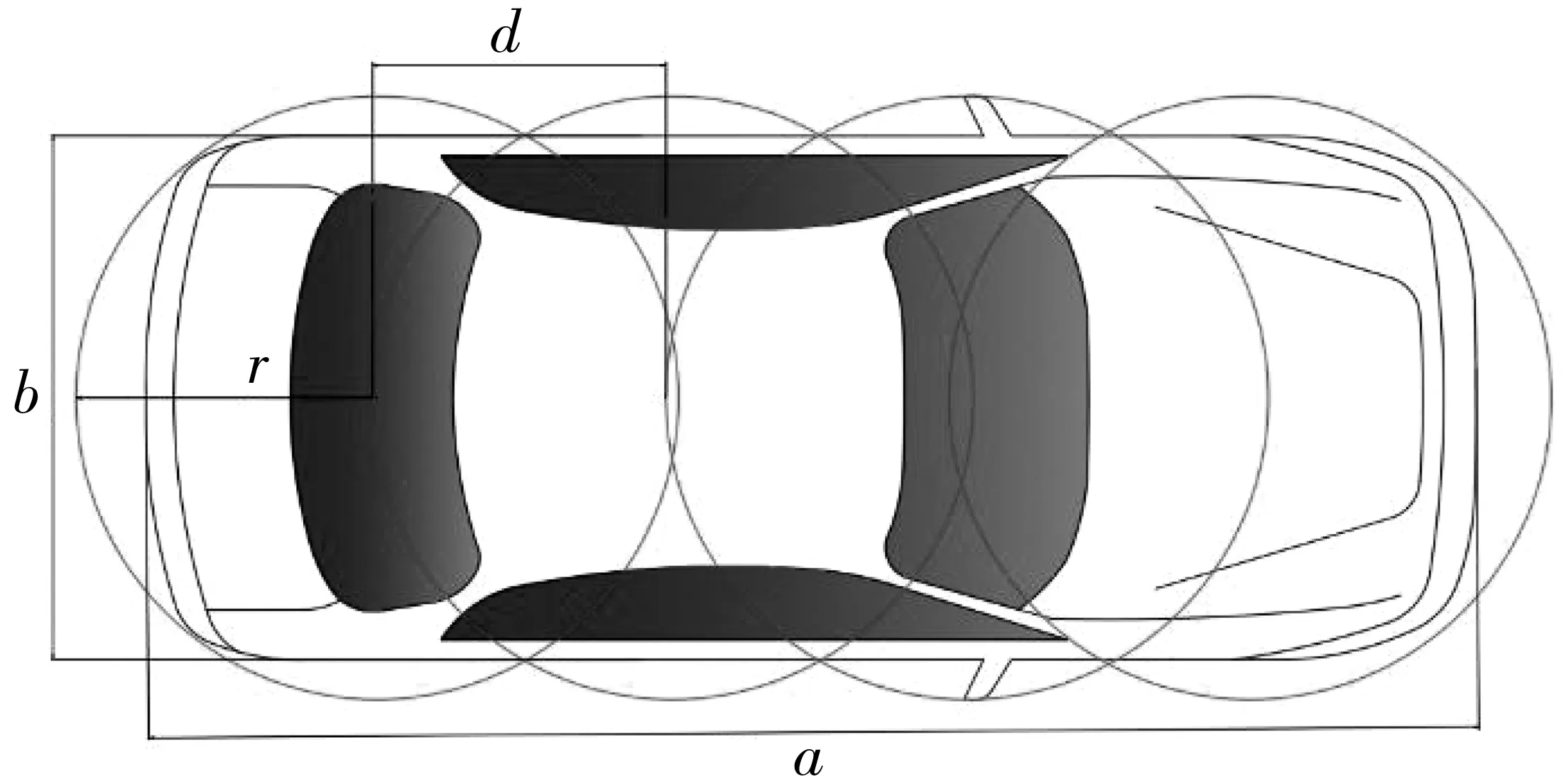
为进一步提高搜索效率,使初始状态和目标状态更快相遇,在随机数刚开始的扩展阶段使用目标偏置策略——即根据随机概率来决定qrand是目标点还是随机点。设定一个目标偏向阈值qprob,在每次节点生长前得到一个0到1的随机值p,当0 RRT算法中的最邻近点的搜索尤其重要,它不但决定了新节点的生长方向,对于全树的收敛也非常重要。查找最近点的基础是计算状态空间内两点之间的距离。计算距离最直观的方法是使用欧氏距离,但对智能汽车来说,这样的定义并不正确,如图8所示,对于某车辆的Ⅰ状态而言,下一时刻,存在Ⅱ、Ⅲ、Ⅳ这3种状态。其中,Ⅱ向左旋转了30°,Ⅲ与Ⅰ距离15 m,Ⅳ与Ⅰ距离40 m,由于车辆本身的动力学约束,车辆不能原地打转也不能横向平移,所以在欧式距离的定义下,离Ⅰ状态最远的Ⅳ状态才是最近的搜索方向点。 图8 最邻近点判断Fig. 8 Judgment of the nearest neighbor point 考虑车辆的动力学约束,笔者在寻找最近点时,首先基于车辆的转向约束在目标偏置的基础上进一步缩小采样空间,然后利用K-D树搜索出几个欧式距离下的最近点,再考虑到车辆的动力学约束,使得到的最近点能够符合最大曲率约束并保证曲率的连续性。如图9,在选择最邻近节点时,虽然qi与qrand之间欧氏距离更近,但是由θi>θj,因此能够使生成的路径更加平滑并且能够保证车辆具有良好的跟随性,所以最终选择qj作为最近邻节点。笔者将随机采样点到邻近点之间的度量函数定义如式(3): 图9 最邻近节点选择示意Fig. 9 Schematic diagram of the selection of the nearest node Ddist=w1D+w2A (3) 式中:D、A分别为归一化后的欧式距离和角度;w1、w2是欧式距离和角度所占权重,可根据实际应用进行设定,据实验的经验数据设定w1=0.55,w2=0.45。dmax和θmax分别表示当前采样区间内距离目标点的最远距离和最大角度,di和θi分别表示当前采样区间内第i个点距离目标点的距离和角度。D、A的值分别为: (4) 由于RRT算法本身的随机采样性,生成的路径通常非常曲折且极度不平滑,常常伴随着抖动且包含很多不必要的节点,尤其是在存在大量形状不规则且分布不均匀的障碍物的复杂环境中,过多的折点会使得智能车无法有效对路径进行跟踪,且频繁转向会影响乘坐舒适性,并加速车辆机械结构的磨损,这对路径规划来说是不可接受的。需对初始的RRT路径进行剪枝和平滑化的后处理工作。 根据车辆的最大曲率约束以及曲率的连续性,对全树T中的安全节点进行删除以达到剪枝的作用,如图10。由图10可知,从q1到q8,q10到q15都是安全的,因此可直接将q1和q8相连,q10与q15相连。若剪枝后的曲线不满足最大曲率约束,则再插入必要的节点。程序仿真的剪枝前后的对比效果如图11。 图10 剪枝原理Fig. 10 Pruning principle 图11 剪枝前后算法Fig. 11 Schematic diagram of the algorithm before and after pruning 在定义与障碍物的安全距离时,碰撞检测是必不可少的重要步骤。采取通过环境地图与车辆构型做卷积校验的检测方法进行碰撞检测,将车辆大致构型为若干半径为r的圆,如图12。进行安全碰撞检测时,需保证每个圆在环境地图中所占据的栅格是安全的,只要有任意一个或几个圆不安全,则需放弃此次生长并插入新的安全节点。 图12 安全碰撞检测Fig. 12 Safe collision detection 图12中,a为车辆的长度,b为宽度,d为两圆心之间的距离,r为圆的半径,圆的相关参数为: (5) 贝塞尔曲线可以生成曲率连续的路径,可以确保车辆能够平稳沿着规划路径行进[13]。采用贝塞尔曲线对最终路径进行拟合和平滑处理,n阶贝塞尔曲线的如式(6): (6) 笔者采用具有两个控制节点的三阶贝塞尔曲线,如式(7): P(t)=(1-t)2P0+2t(1-t)P1+t2P2 (7) 式中:P0、P1、P2是指控制点的个数;t为一个在0到1的值,控制曲线的曲率。 为了验证算法的有效性、实时性和适应性,笔者进行了仿真实验进行验证。仿真实验的全部算法用C++语言编写,在搭载Intel© Core i7-8950H,16G内存的笔记本电脑上完成。设定车辆车头朝向为箭头所指方向,左下角为起始方向,右上角为目标方向,障碍物区域为黑色。图13分别是基本RRT,Bi-RRT和改进后的Bi-RRT 3种算法分别在简单障碍物及复杂障碍物情况下对同一规划问题的求解结果。从仿真结果可以看出,改进后的Bi-RRT使得多余的节点生成数量大大减少,因此算法所需要的计算开销明显变少。而且生成路径的曲率更加平缓,更符合车辆的动力学约束。 图13 算法仿真效果对比Fig. 13 Comparison of algorithm simulation results 在复杂仿真环境下分别对3种算法进行了100次规划,并记录生成路径所需的平均时间、生成的节点数目以及成功率,如表1。由表1可知,经过改进的Bi-RRT算法,在实时性以及节点数目的生成方面都有很大改进。此外,由于增加了约束,算法在成功率方面则略有下降,但依然能够满足实时性的要求。 表1 不同算法的时间、节点数目、成功率对比Table 1 Comparison of time, number of nodes and success rate ofdifferent algorithms 图14(c)为3种算法生成路径的曲率变化。由图14可知,与笔者提到的基本RRT和基本Bi-RRT算法相比,笔者提出的算法所生成的路径的曲率变化是更加平缓且平滑的,因此能够满足车辆的转向约束。 图14 归一化路径曲率对比Fig. 14 Comparison of normalized path curvature 综合表1和图14可以看出,改进后的Bi-RRT不论是在算法的搜索速度还是算法开销上都有显著的提升,搜索的路径相对来说也更加平缓,这两点在复杂障碍物环境下显得尤为明显。并且所生成的可执行路径的曲率也非常符合车辆动力学要求,所以该算法是正确且有效的。 1)智能汽车一直是国内外的研究热点,也是智能交通智慧出行的重要组成部分。路径规划在智能汽车研究问题中起着承上启下作用,是感知与控制之间的桥梁。笔者提出的基于Bi-RRT改进的规划算法,利用Bi-RRT的快速搜索性结合车辆的转向约束,能够实时有效的规划出在复杂环境下智能汽车车辆的运动路径并具有良好的跟随行。 2)与传统的RRT算法相比,由于利用车辆的动力学特性在节点生成时进行了约束,从而使得所生成的路径的曲率能够很好的满足车辆的转向要求。仿真实验证明了算法的有效性、实时性和适应性。笔者所提出的算法不仅仅适用于无人驾驶汽车,也适用于其他的机器人路径规划问题。此外,该算法目前适用于低速场景下的路径规划问题,下一步将会尝试解决高速场景下的路径规划问题,以便更好的满足实际工程需要。2.4 考虑转向约束的最邻近点扩展策略
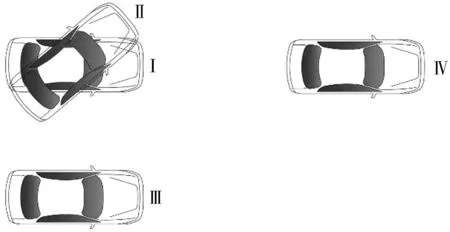
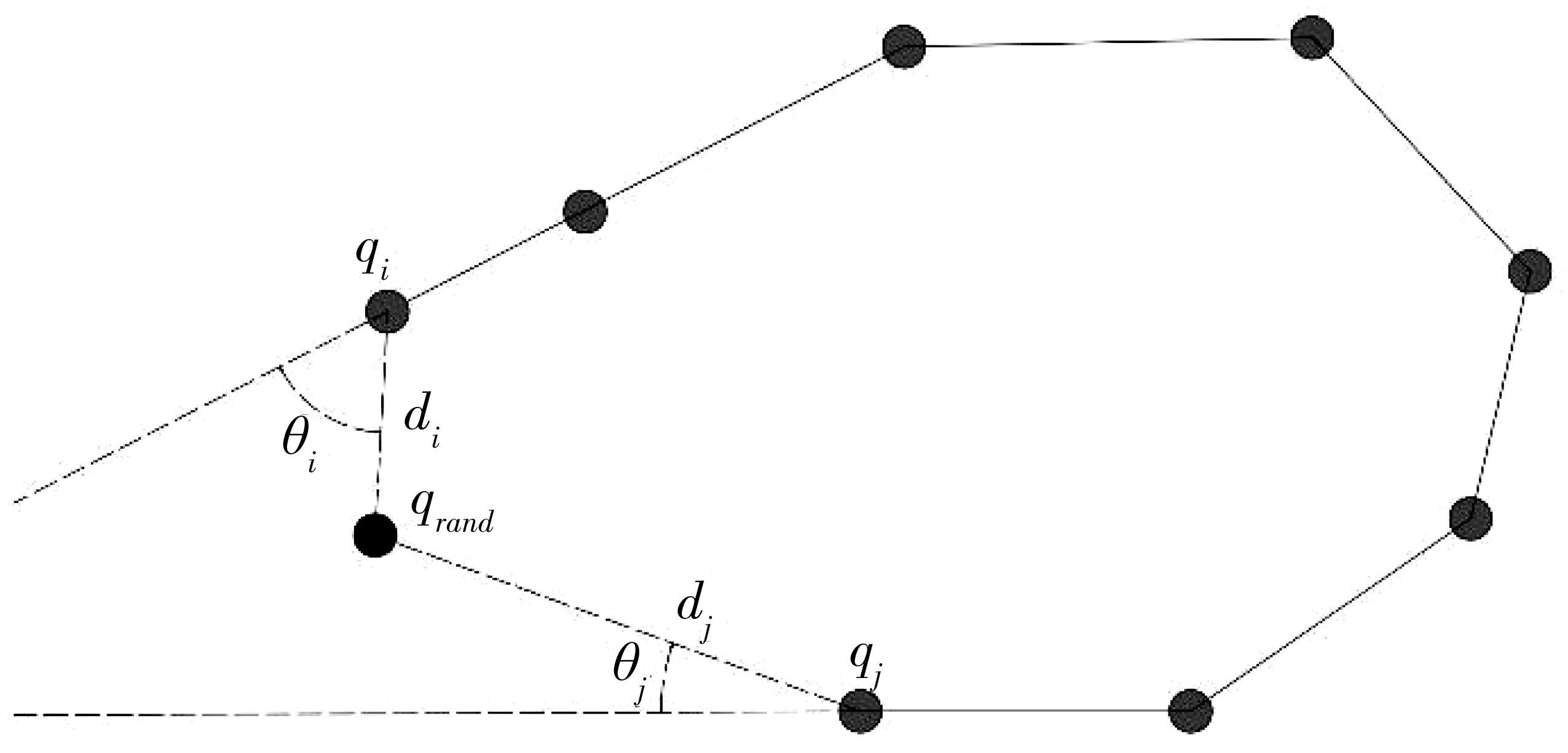
3 后处理方法
3.1 剪枝处理

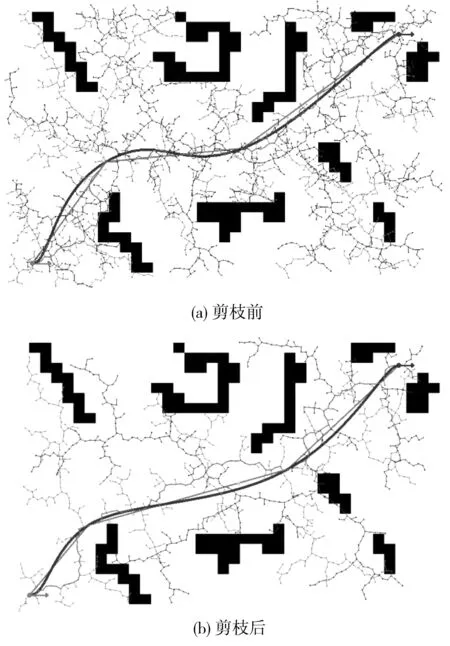
3.2 碰撞检测
3.3 贝塞尔曲线平滑函数
4 仿真实验



5 结 论
