基于动态神经网络的旋翼飞行器在线模型辨识算法

聂文明，梅 彬

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

飞行器动力学模型对飞行控制系统的设计至关重要，更高精度和准确度的动力学模型可大大降低飞控系统的设计难度，改善飞控系统的性能。然而对于实际飞行器，尤其是大型旋翼飞行器而言，其结构、系统的复杂性使得其动力学模型非线性强、复杂度高，导致难以建立精确的动力学模型。此外，模型参数偏差和多源外部干扰导致的未知不确定性给建模带来了挑战。

传统的建模思路是基于空气动力学和飞行力学原理，逐步推导飞行器的6自由度动力学模型。但如前所述，飞行器自身的复杂性导致上述建模存在重重困难。为实现建模的目的，往往需要做出种种假设以降低建模难度，但这也不可避免地引入了建模偏差，且建模过程往往需要进行大量的测量、风洞试验、飞行验证和模型改进，需要投入大量的人力和财力。

与之相对的是基于系统辨识技术的建模思路。该思路基于飞行试验数据，通过离线或在线的方式，运用辨识方法和算法，建立符合飞行器的辨识模型。该类思路更多地依赖于数据，而对动力学知识及人力和财力的要求远低于传统思路，且可以实现对模型的快速修正和改进，为缩短研究周期和降低研制成本提供了可行的途径。现有方法可分为离线线性模型辨识和在线线性模型辨识两类。文献[3]针对一类小型直升机的模型辨识问题，提出了一类基于频域方法的线性模型辨识方法。旋翼飞行器非线性模型的在线辨识算法研究成果较少。

在前人研究的基础上，本文提出了一种基于动态神经网络的旋翼飞行器在线模型辨识算法。该算法不依赖于动力学模型的先验知识以及未知不确定性的信息，可在存在位置不确定性(模型参数偏差及外界干扰)的情况下，实现旋翼飞行器非线性模型的在线高精度辨识。文章最后进一步从理论分析和数值仿真的角度，证明了所提算法的收敛性、辨识快速性和辨识精度。

1 飞行器运动模型

本文以某类旋翼飞行器为研究对象开展研究，其运动模型如下：

(1)

其中：

x

，

y

，

z

分别为飞行器沿三个轴向的位置，

φ

，

θ

，

ψ

分别为俯仰、滚转和偏航角，

u

，

u

，

u

，

u

，

Ω

为控制量；

I

，

I

，

I

分别为飞行器在三个轴向的转动惯量，

J

为转动惯量，

k

，

k

，…，

k

分别为空气阻力系数，

l

为操纵力力臂，

m

为飞行器质量，

g

为重力加速度。

为表述方便，将上述运动模型改写为如下形式：

(2)

对于实际飞行器而言，均存在模型参数偏差和外界干扰导致的模型不确定性，则在考虑不确定性的情况下，上述理想的标称模型实际可表示为如下形式

(3)

其中，

ε

表示模型不确定性。由于上述不确定性是未知的，所以难以建立精确的飞行器数学模型，给飞行控制器的设计带来了困难。

为解决上述问题，本文基于动态神经网络，提出了一种数据驱动的旋翼飞行器模型辨识算法，实现了模型的在线实时辨识，解决了存在位置不确定性情况下的模型不可得问题。

2 旋翼飞行器在线模型辨识算法

本节首先基于动态神经网络，给出了旋翼飞行器在线模型辨识器设计方法；然后基于Barbalat引理，给出了辨识误差渐进收敛性的理论证明。

2.1 基于动态神经网络的模型辨识算法设计

辨识器表达式：

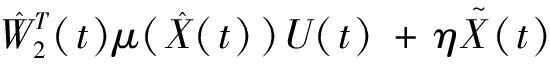
(4)

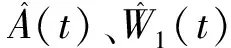
(5)

其中，

σ

∈

R

，表示神经网络的重构误差。

为实现上述设计目标，设计权重矩阵的在线更新律如下：

(6)

其中，

Λ

∈

R

，

i

=1，2，3，均为正定学习速率矩阵。基于上述权重矩阵更新率，辨识器可实现对飞行器模型的在线实时辨识，辨识器的收敛性分析将在下一小节给出。

2.2 辨识算法收敛性分析

本小节将给出上述辨识算法收敛性的理论分析。

假设

1.辨识器理想权值矩阵

A

、

W

和

W

均有界，及存在正常数

c

、

c

和

c

,使得如下不等式成立：

(7)

假设

2.存在正常数

c

，使得辨识器重构误差

σ

的上界可由如下不等式表示：

(8)

定理

1 在假设1和假设2均满足的情况下，若辨识器权重矩阵依据式(6)所示的权重更新率进行在线更新，且涉及参数

η

满足如下不等式：

(9)

证明：

联立式(4)所示的辨识器近似式和式(5)所示的辨识器理想式，可得辨识误差的动态模型如下：

(10)

定义如下Lyapunov函数：

其中，tr(·)代表矩阵的迹。

根据式(6)所示的辨识器权重矩阵更新律和式(10)所示的辨识误差动态模型，并结合矩阵迹的性质可得上式

V

相对时间

t

的导数如下：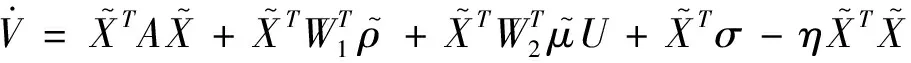

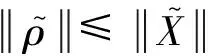
结合Cauchy-Schwarz不等式和上式可得：

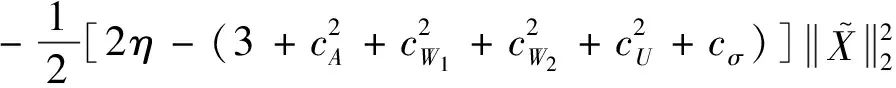
(11)

因此，只要设计参数

η

满足如下不等式：

证毕。

3 仿真分析

本节通过数值仿真，进一步验证所提出的旋翼飞行器在线模型辨识算法的有效性。仿真环境采用matlab2016b，仿真基于某类旋翼飞行器航模展开，仿真中采用的状态量初始值和标称模型各项参数如表1所示。

表1 飞行器模型状态量初始值和标称模型参数值

对于模型辨识算法而言，有两方面的关键性能：一方面是辨识算法的辨识速度和辨识精度；另一方面是辨识算法在模型存在不确定性及未知干扰的情况下的有效性。为验证辨识算法以上两方面的关键性能，分别进行如下两组仿真试验。

3.1 存在模型不确定性情况下的算法有效性仿真

设置辨识器的初始辨识误差和模型参数偏差如表2所示。限于篇幅，仿真中仅给出了一类初始辨识误差和参数偏差(

I

误差)的仿真结果，但本文所提算法对不同初始辨识误差和其他偏差(包括质量、弦长、阻力系数和其他转动惯量)的情况同样可以实现对飞行器模型的在线实时的高精度辨识。

表2 初始辨识误差与模型参数偏差

基于上述仿真条件，数值仿真结果如下。其中，令

X

表示旋翼的标称模型(

I

=0.05kg·m)积分得出状态量。图1给出了旋翼飞行器的三维飞行轨迹(

x

-

y

-

z

)仿真结果。对比标称模型积分得到的飞行轨迹和实际模型积分得到的飞行轨迹可以看出，转动惯量偏差对飞行器飞行轨迹有显著影响；而由辨识器辨识所得轨迹可以看出，尽管存在较大的初始辨识误差，但通过在线实时辨识，辨识所得的近似轨迹快速地实现了对真实轨迹的高精度辨识。

图1 存在惯量偏差情况下的飞行器飞行轨迹图(x-y-z)

进一步结合图1和图2可以看出，尽管标称模型不存在初始状态量偏差，但随着飞行器飞行时间的变长，转动惯量偏差最终导致模型误差逐渐变大。反观辨识误差，尽管存在初始辨识误差，但验证了辨识算法在飞行初期通过在线更新权重矩阵，快速(<0.001s)消除了辨识误差，且飞行全程均能保证模型辨识误差在很小的范围内。图3-图5同样说明了上述分析结果，其中图4则给出了辨识器同样可以快速消除初始的姿态角辨识误差。

图2 存在惯量偏差情况下的飞行器位置误差

图3 存在惯量偏差情况下的飞行器速度误差

图4 存在惯量偏差情况下的飞行器姿态误差

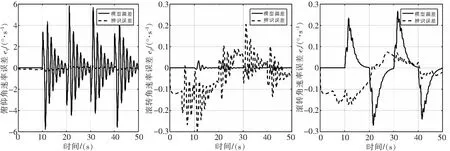
图5 存在惯量偏差情况下的飞行器姿态角速率误差

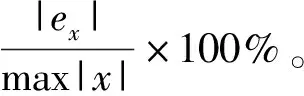
表3 最大模型误差与最大辨识误差及其百分比统计表(惯量偏差情况)

综上所述，本文所设计的旋翼飞行器在线模型辨识算法可以针对存在未知不确定性的情况，完成飞行器模型的实时高精度辨识。

3.2 存在未知干扰情况下的算法有效性仿真

设置辨识器的初始辨识误差和未知气动干扰如表4所示。

表4 初始辨识误差与未知气动干扰

图6-图10给出了存在气动干扰情况下的仿真结果。可以看出，基于动态网络的在线辨识算法依然保持了高精度(见表5)的快速(误差收敛时间<0.001s)辨识。

图6 存在气动干扰情况下的飞行器飞行轨迹图(x-y-z)

图7 存在气动干扰情况下的飞行器位置误差

表5 最大模型误差与最大辨识误差及其百分比统计表(气动干扰情况)

图8 存在气动干扰情况下的飞行器速度误差

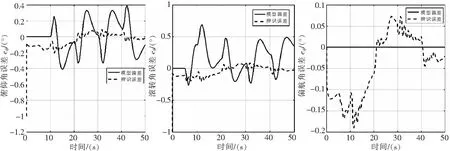
图9 存在气动干扰情况下的飞行器姿态误差

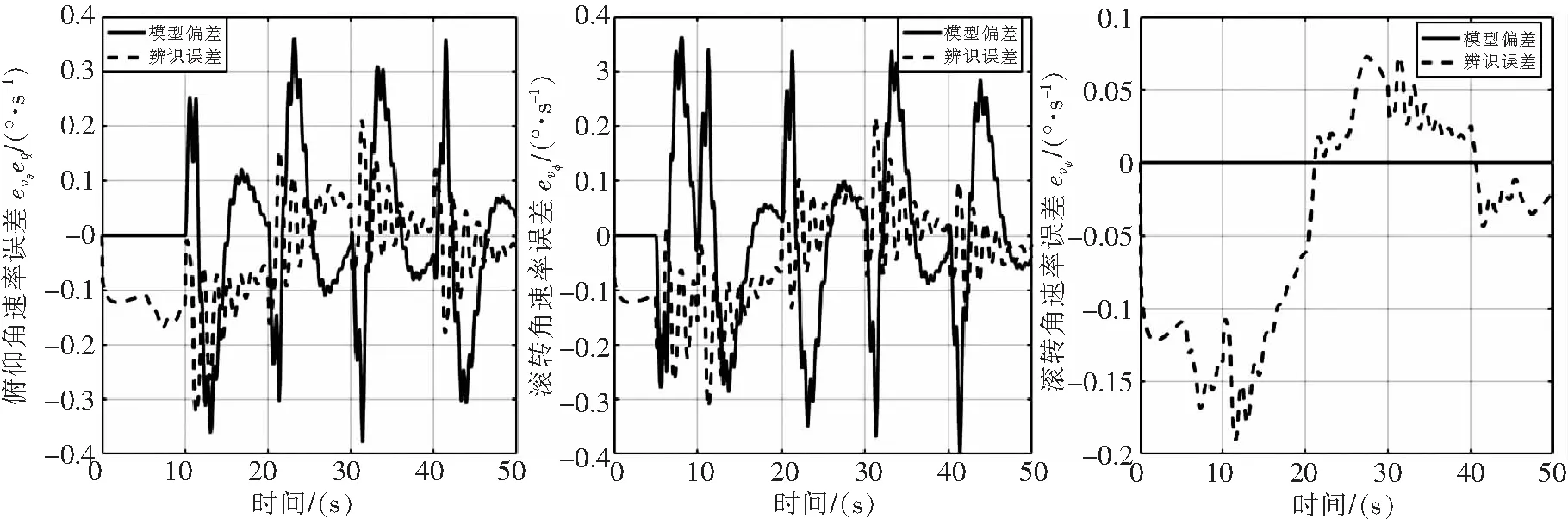
图10 存在气动干扰情况下的飞行器姿态角速率误差

4 结论

旋翼飞行器动力学模型复杂度高，非线性强，且存在模型参数偏差以及外界干扰导致的未知不确定性，因此难以建立精确的动力学模型。本文提出了基于动态神经网络的旋翼飞行器在线模型辨识算法，实现了不依赖于模型先验信息、完全数据驱动的在线实时(<0.05s)高精度的模型辨识，算法结构简单，计算量低。并且，分别从理论分析和数值仿真验证的角度，验证了所提出的模型辨识算法的收敛性、快速性和高辨识精度等性能，为解决复杂旋翼系统的动力学建模问题提供了可供参考的途径。