ZV-ZCS DC/DC移相全桥变换器拓扑与设计

陈仲伟 李奎 程怡捷 汪洪亮 冷阳 刘浩田

如今，由于能源枯竭和大气污染问题，以光伏发电、风力发电与电动汽车为代表的清洁能源生产与利用方式得到了广泛关注和应用. DC/DC直流变换器作为储能、充电等场合的重要电能变换环节，其可靠性、效率与功率密度等性能对新能源的高效利用起着关键作用[1-3].  DC/DC移相全桥变换器作为直流变换器中的主流拓扑，具有大功率、高效率、高可靠性等优点，在动力电池充电、新能源储能与并网等场合均得到了广泛应用. 由于移相全桥变换器具有零电压开通（Zero-Voltage Switching，ZVS）特性，开关损耗大大降低，结合宽禁带器件，可使变换器的开关频率得到大幅度提升，故而降低变压器等无源元件的体积，因此变换器往高频化、小型化的趋势发展，更加有效地契合了当前的能源应用需求[4-6].

传统移相全桥变换器如图1所示，S1～S4为原边侧4个开关管，Vh为原边侧逆变桥输出电压，Le为高频变压器漏感，ILe为漏感电流，D5 ～ D8为副边4个整流二极管，Lf和Cout分别为输出滤波电感和电容，R为负载电阻. 对于该变换器，其滞后桥臂开关管ZVS的实现依靠原边侧漏感能量，当轻载时，ILe较小，漏感储存能量小，滞后桥臂开关管难以实现ZVS[7]，影响了变换器的可靠性与效率[8]，对于副边二极管，其关断时电流高，存在严重的反向恢复问题，二极管尖峰电压高[9-10]. 文献[11-12]通过利用在原边侧串入饱和电感增加了滞后桥臂软开关实现范围，但导致占空比丢失问题严重，电流应力上升. 文献[13-15]通过在滞后臂上构造由电感和电容组成的辅助谐振网络，实现滞后桥臂的ZVS，但辅助网络增加了电路的复杂性与成本. 文献[16]通过在原边侧添加电容，组成串联谐振网络，通过调频来实现轻载ZVS. 文献[17]采用三绕组耦合电感，用以提供宽负载范围下ZVS实现的能量. 文献[18]通过实时改变死区时间，以拓宽变换器的ZVS范围，但该死区时间的计算依赖于变换器模型，计算量大，增加了控制的难度. 文献[19]针对车载充电应用场合，提出了移相全桥变换器与LLC谐振变换器集成架构下的充电控制方法，以保证移相全桥变换器滞后桥臂在轻载时仍能保证ZVS的性能，但该方法仅针对具有高低压电池的充电场合，其应用范围具有一定的局限性. 文献[20]通过对励磁电感进行设计，以保证最小的ZVS实现电流，但该励磁电感会导致重载工况时无功环流加大，降低变换器效率.

双有源桥移相全桥变换器如图2所示，该变换器原副边分别采用双向开关S1～S4和S5～S8，有效保障电流的双向流动，桥臂输出电压Vh1和Vh2和电流ILr解耦，工作模态简单且原边侧移相角、副边侧移相角和原副边移相角差均可独立设置，存在3个控制自由度，控制灵活[21-22]，适用于宽输入输出范围的应用场合[23-24]，能够实现宽负载范围内的ZVS性能[25]，保证其高效率特性.

结合图1和图2拓扑的特点，本文通过将图1中的滤波电感Lf前移至原边侧作为谐振电感Lr，实现了重载下原边开关管ZVS，副边二极管自然续流到零，轻载下超前桥臂开关管实现ZVS，滞后桥臂开关管实现零电流开通与关断（Zero-Current Switching，ZCS），副边二极管工作于电流断续模式（Discontinuous Conduction Mode，DCM），实现了ZCS性能，提升了变换器的效率与可靠性. 与双有源桥变换器不同，针对单向能量传输场合，本文提出的ZV-ZCS型移相全桥变换器的副边开关管均简化为二极管，副边的方波电压由流过变压器原边侧的电流极性决定，电压和电流存在耦合关系，针对双有源桥变换器的工作模态与设计法则不再适用于该拓扑. 本文通过阐述该变换器的工作模态，分析其ZV-ZCS的实现机理，通过推导其不同模式下的增益表达式，给出了主要参数的设计准则，最后通过PSIM仿真与2 kW的实验样机验证了该变换器的工作特性与理论分析的正确性.

1   ZV-ZCS型移相全桥变换器拓扑

图3所示为ZV-ZCS型移相全桥变换器拓扑图，其中，S1 ～ S4为原边侧4个开关管，D1 ～ D4分别为开关管的内部反并联二极管，C1 ～ C4分别为开关管的内部寄生输出电容. Lr为原边侧谐振电感，ILr为流经Lr上的谐振电流，通过利用谐振电感Lr，在功率管的开通过程中，与主电路中开关管的寄生电容谐振以实现ZVS软开关[26-28]. T1为高频变压器，其原副边变比为1 ∶ n，D5 ～ D8为副边整流二极管，ID5 ～ID8分别为整流二极管上的电流，Irect为整流电流. Vh为逆变桥臂输出电压，Vin与Cin分别为输入电压与输入滤波电容，Vout与Cout分别为输出电压与输出滤波电容，R为负载电阻.

S1 ～ S4每个开关管均为0.5的导通占空比，其中同一桥臂的上下两个开关管互补导通，对角开关管的导通相角差即为移相角，输出电压的幅值取决于该移相角. 若S1超前S4导通，则称S1与S2所在桥臂为超前桥臂，S3与S4所在桥臂为滞后桥臂. 当移相角为0°时，Vh为两电平方波，当移相角介于0°～180°时，Vh为带有零电平形式的三电平方波. 因此通过调整移相角，调节Vh的占空比，从而调节输出电压Vout .

1.1   拓扑CCM工作模态

对于该拓扑的工作模式，可以劃分为电感电流连续模式（Continuous Conduction Mode，CCM）与电感电流断续模式（DCM），CCM和 DCM均可分解为8个工作模态，图4和图5为CCM下的工作模态，当处于CCM模式下，原边侧4个开关管开通均实现ZVS，副边二极管电流自然过零. 图6和图7为DCM下的工作模态，当处于DCM模式下，原边开关管超前桥臂开通实现ZVS，滞后桥臂开关管开通与关断均实现ZCS，并且副边整流二极管工作于断续模式，实现ZCS，有效抑制二极管反向恢复问题. 下面将对CCM与DCM下的工作模态进行详细阐述，并分析原边侧开关管ZV-ZCS、副边二极管ZCS的实现机理.

图4为CCM模式下开关周期内电压电流的波形图，图5为CCM模式一个开关周期内不同的工作模态，由于前半个周期和后半个周期一致，故取前半个周期进行分析.

模态1[t0 ～ t1]：如图5（a）所示，开关管S1和S4导通，S2和S3关断，逆变桥臂输出电压Vh = Vin，谐振电感Lr储能，电感电流线性上升如式（1）所示，此时二极管D5和D8导通，功率传输至负载侧.

模态2[t1 ～ t2]：如图5（b）所示，该模态为死区时间，从开关管S1关断时开始，ILr方向仍为正，且为开关管S1的寄生电容C1充电，并对开关管S2的寄生电容C2放电，从而实现了开关管S2的零电压开通.

模态3[t2 ～ t3]：如图5（c）所示，当开关管S2零电压开通后，逆变桥臂输出电压Vh = 0，此时谐振电感Lr释能到负载侧，电流线性下降如式（2）所示.

模态4-1[t3 ～ t4]：如图5（d）所示，该模态处于模态4的死区时间，从开关管S4关断时开始，ILr仍为正向，其对开关管S4的寄生电容C4充电并对开关管S3的寄生电容器C3放电，为S3的零电压开通提供了条件.

模态4-2[t3 ～ t4]：如图5（e）所示，当开关管S3零电压开通后，谐振电感Lr能量向负载与电源侧馈送，ILr快速下降如式（3）所示，当电感电流下降到0并且换向时，二极管D5与D8续流到0，从而关断，有效削弱了二极管的反向恢复问题.

1.2   拓扑DCM工作模态

图6为DCM模式下开关周期内电压电流的波形图，图7为DCM模式一个开关周期内不同的工作模态，DCM的模态1、模态2与模态3与CCM的完全一致，这里不再赘述，仅对模态4与模态5进行阐述.

模态4[t3～t4]：如图7所示，ILr在模态3续流到0，模态4由于逆变桥臂输出电压Vh = 0，故而ILr保持为0，副边整流二极管进入断续模式，实现ZCS，故而抑制了反向恢复问题，负载由输出滤波电容Cout供能.

模态5[t4 ～ t5]：该模态为S4关断后，S3开通前的死区时间，S4关断时，ILr为零，因此S4的关断与S3的开通均实现ZCS，从而减小了开关损耗.

2   拓扑参数设计

对于该拓扑，副边的方波电压由流过变压器原边侧的电流极性决定，即由电感电流极性决定，电压和电流存在耦合关系，电压增益不再是占空比的线性函数，本节将对该电路处于CCM与DCM模式下的电压增益分别作详细探讨并给出谐振电感Lr与变压器变比n的设计法则. 为简便计算，作以下假设：

1）变压器、开关管与二极管均为理想模型.

2）计算过程忽略死区影响.

3）输入电压与输出电压纹波忽略不计.

4）设fs为开关频率，1 ∶ n为原副边变比，D为半周期内Vin或-Vin电平占比.

5）β为CCM模式下，逆变桥臂输出Vin电平时电流ILr大于0的时间占比或-Vin电平下电流ILr小于0的时间占比.

6）λ为DCM模式下，逆变桥臂输出Vin电平时电流ILr大于0或者-Vin电平电流ILr小于0的时间占比.

2.1   电压增益

对于CCM模式，谐振电流ILr为连续模式，正半周期间，对谐振电感Lr列伏秒平衡方程，如式（4）所示，对输出滤波电容Cout列安秒平衡方程，如式（5）所示，综合式（4） （5），可得CCM下的电压增益如式（6）所示.

对于DCM模式，谐振电流ILr为断续模式，正半周期间，对谐振电感Lr列伏秒平衡方程，如式（7）所示，对输出滤波电容Cout列安秒平衡方程，如式（8）所示.

对于CCM与DCM模式，存在一个电流临界模式（Boundary Conduction Mode，BCM）的过渡点，对于该点谐振电感Lr伏秒平衡方程如式（10）所示，输出滤波电容Cout安秒平衡方程如式（11）所示.

由CCM、DCM与BCM的增益可知，电压增益是占空比D、负载电阻R、谐振电感Lr、开关频率fs与变比n的函数，该函数形式复杂，物理意义不直观. 为方便描述D与R的关系，对表1所示参数下增益进行计算，并绘制图8所示的增益为0.75时，D与R的关系曲线. 可知，当R越大（负载越轻）时，占空比越小，变换器越容易进入DCM模式，当R越小（负载越重）时，占空比越大，变换器越容易进入CCM模式. 当R小到一定值时，变换器已无法获得0.75的直流增益. 因此变换器在进行参数设计时，需要考虑其最大负载功率以获得所需增益，这是该变换器与传统移相全桥变换器的不同之处.

变换器在不同负载下进入不同模式（CCM与DCM）的物理意义与Buck变换器相似，当负载较重时，输出电流大，导致ILr峰值电流高，在逆变桥臂输出电压Vh = 0时，ILr未降低到0，因此其在开关周期内工作于CCM模式;而当负载较轻时，输出电流小，ILr峰值电流小，在逆变桥臂输出电压Vh = 0时，ILr降低到0，产生断续模态，因此其在开关周期内工作于DCM模式.

2.2   变比n与谐振电感Lr设计

由CCM与DCM的增益可知，電压增益是占空比D、负载R、谐振电感Lr、开关频率fs与变比n的函数，函数形式复杂，不利于参数设计. 但由上文分析可知，当负载越重时，占空比D越大，越容易进入CCM模式，反之则进入DCM模式. 为降低电流应力，防止过裕量设计，故应满足式（12）所列方程.

对于该拓扑工作的BCM过渡点，其实质为隔离型Buck电路，因此定义该点对应的D即可确定变压器变比n，若该点对应D太小，变比n大，容易导致系统过裕量设计并且电流应力大，若该点对应D太大，变比n小，为保证同等增益，谐振电感Lr取值小，亦导致电流应力大. 综合以上原因，可取最小临界D在0.4～0.6之间进行设计.

现就一系统需求如表2所示对电路拓扑参数及性能作出设计与分析，首先当输入电压Vin最大时，输出电压Vout最小，定义此时BCM点出现在D为0.4～0.6，代入式（10），推出变比n介于0.95～1.3，再联立式（12），得出谐振电感Lr的范围为45～78 μH，此时对应n与谐振电感Lr均为边界值，在边界内，变比n与谐振电感Lr的任意组合不一定满足增益要求，可能导致系统过裕量设计或达不到增益值要求. 联立式（6） （9），得到关于变比n与谐振电感Lr不同组合下，对应的D的三维图，如图9所示，通过该图可以直观看到Vin = 420 V与380 V下，Vout = 300 V，P = 2 kW时对应的占空比D，当D = 1时，则代表无法达到增益要求，当D很小就可以达到增益要求时，说明系统过裕度设计.

对于同时满足增益要求、裕度又合理的变比n与谐振电感Lr的组合，通过计算对应的电流应力，如式（13）所示选择最小电流应力下的n与谐振电感Lr.

最终可得到n = 1.07、Lr = 60 μH的计算结果，在该组参数下，不同输入、不同负载工况下对应的占空比D与ZV-ZCS区域如图10所示. 当Vout = 240 V时，最大占空比出现在Vin = 380 V，P = 2 kW下，D =0.7，当Vout = 300 V时，最大占空比出现在Vin = 380 V，P = 2 kW下，D = 0.92，全负载、全输入工况均可達到要求，并且裕度合理. 以上两种输出工况，在轻载时，占空比较小，为ZV-ZCS区域;当负载变重，占空比上升，则进入ZVS区域.

3   仿真分析

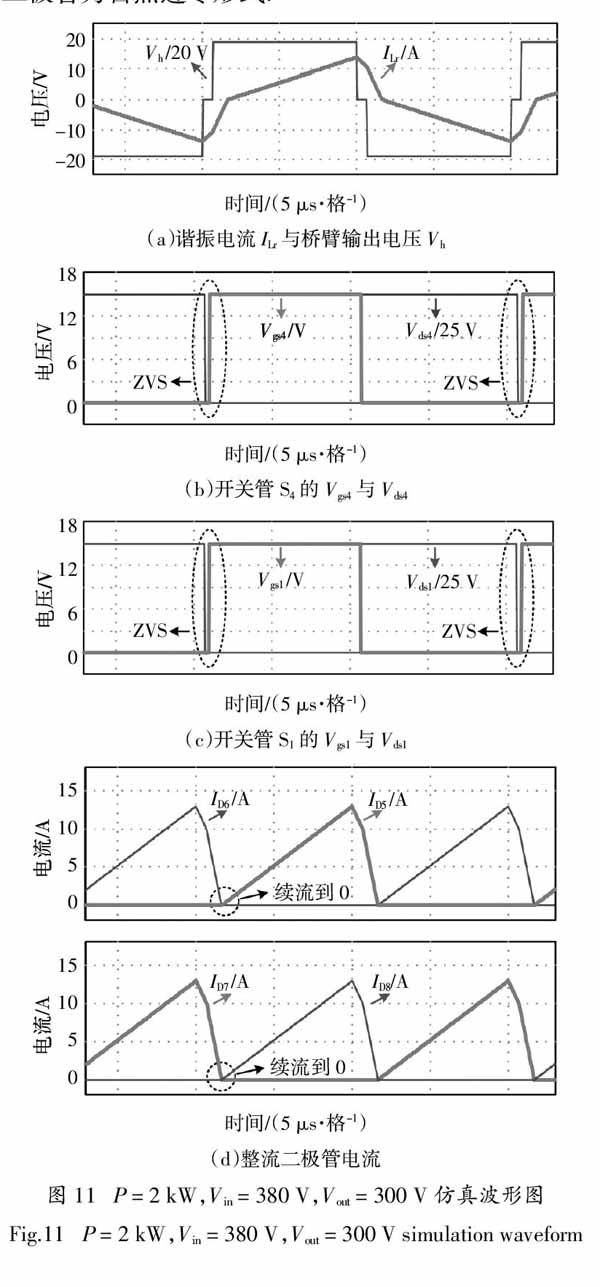
基于上文对该变换器的工作模态与增益的分析，本节通过PSIM软件平台进行仿真验证，仿真参数如表3所示，通过在Vin = 380 V，Vout = 300 V输入输出工况下，对变换器的满载与半载功率下进行仿真，验证其工作模态、占空比以及ZV-ZCS区域与理论分析的一致性. 该仿真的输入输出工况为输入最低，输出最高，因此增益最大，只要该工况满足增益要求，其他工况均满足要求，由于篇幅有限，因此不再对其他的输入输出工况进行仿真.

图11为满载仿真波形，图11（a）为谐振电流ILr与桥臂输出电压Vh的波形图，可知Vh的占空比D = 0.93，ILr为CCM模式，ILr始终滞后于Vh，这意味着原边侧4个开关管均实现的ZVS.

图11（b）为滞后桥臂开关管S4的驱动电压Vgs4与漏源电压Vds4波形，可见在Vgs4驱动为高电平前，Vds4已降低到0，因此S4实现了ZVS. 而对于开关管S3，其软开关特性与S4一致，故不再用仿真进行说明.

图11（c）为超前桥臂开关管S1的驱动电压Vgs1与漏源电压Vds1波形，可见在Vgs1驱动为高电平前，Vds1已降低到0，因此S1实现了ZVS. 而对于开关管S2，其软开关特性与S1一致，故不再用仿真进行说明.

图11（d）为整流二极管D5 ～ D8电流波形，可见二极管为自然过零形式.

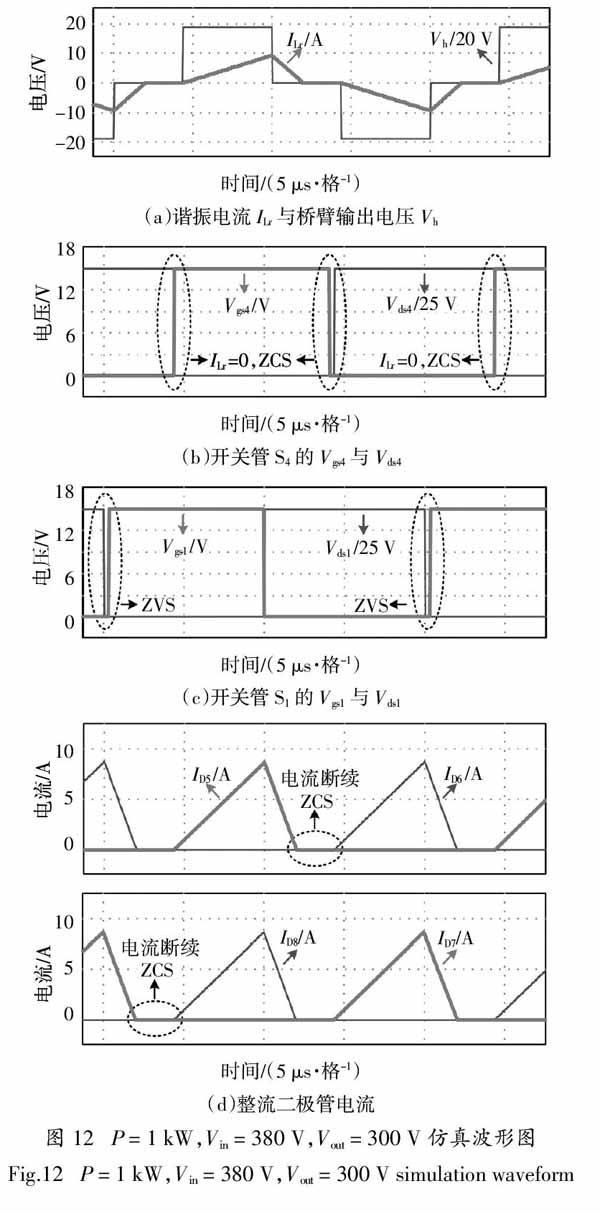
图12为半载仿真波形，图12（a）为谐振电流ILr与桥臂输出电压Vh的波形图，可知Vh的占空比D = 0.59，ILr为DCM模式，ILr在V = 0的模态内下降为0并且保持，直至Vh变为Vin或-Vin，ILr才开始变化，因此对于滞后桥臂的开关管S3与S4而言，其开通与关断均为ZCS.

图12（b）为滞后桥臂开关管S4的驱动电压Vgs4与漏源电压Vds4波形，可见在Vds4由高电平变为0电平（开通时刻）与Vds4由0电平变为高电平（关断时刻），ILr始终为0，因此推出开关管S4的开通与关断均实现了ZCS. 而对于开关管S3，其软开关特性与S4一致，故不再用仿真进行说明.

图12（c）为超前桥臂开关管S1的驱动电压Vgs1与漏源电压Vds1波形，可见在Vgs1驱动为高电平前，Vds1已降低到0，因此S1实现了ZVS. 而对于开关管S2，其软开关特性与S1一致，故不再用仿真进行说明.

图12（d）为整流二极管D5 ～ D8电流波形，可见二极管电流为断续模式，因此实现了关断时刻的ZCS性能.

由于输出滤波电容Cout的电流纹波值较高，需对其电压纹波值进行考量，以满足工业应用对纹波电压的要求. 图13展示了输出电压Vout在满载下与半载下的波形，其纹波值分别为73 mV（0.024%）与60 mV（0.02%），对于电动汽车充电场合，输出电压纹波要求[29]为1%，可见该拓扑及设计参数能保证合理的电压纹波值.

4   实验结果

基于上文的分析和结论，在实验室环境下搭建了一台2 kW的实验样机，同仿真的验证思路，实验分别在Vin = 380 V，Vout = 300 V输入输出工况下，在变换器的满载与半载功率下进行实验，验证其工作模态、占空比以及ZV-ZCS区域与理论分析与仿真的一致性.

图14为满载仿真波形，图14（a）为谐振电流ILr，桥臂输出电压Vh与副边整流电流Irect的波形图，由于二极管电流不易测试，而Irect为二极管电流流出至输出电容Cout的电流，其可表征二极管电流的特性. 由波形图可知Vh的占空比D = 0.85，ILr与Irect为CCM模式，ILr始终滞后于Vh，这意味着原边侧4个开关管均实现了ZVS，Irect续流到零，表征了二极管的电流具有自然过零特性.

图14（b）为滞后桥臂开关管S4的驱动电压Vgs4与漏源电压Vds4波形，可见在Vgs4驱动为高电平前，Vds4已降低到0，因此S4实现了ZVS. 而对于开关管S3，其软开关特性与S4一致，故不再用实验进行说明.

图14（c）为超前桥臂开关管S1的驱动电压Vgs1与漏源电压Vds1波形，可见在Vgs1驱动为高电平前，Vds1已降低到0，因此S1实现了ZVS. 开关管S2的软开关特性与S1一致，故不再用实验进行说明.

图15为半载实验波形，图15（a）为谐振电流ILr，桥臂输出电压Vh与副边整流电流Irect的波形图. 由波形图可知Vh的占空比D = 0.51，ILr与Irect为DCM模式，这意味着原边侧超前桥臂开关管实现了ZVS，而滞后桥臂开关管实现了ZCS. Irect为DCM模式表征了二极管工作于DCM模式，其具有ZCS特性. 对比图12（d）所示的仿真图，实验中，ILr与Irect在断续模态内出现了高频振荡，这是由于高频变压器上的寄生电容与谐振电感Lr谐振的结果，该振荡峰值很小，仍可认为滞后桥臂开关管与整流二极管获得了ZCS性能.

图15（b）为滞后桥臂开关管S4的漏源电压Vds4、谐振电流ILr与桥臂输出电压Vh的波形，可见在Vds4由高电平变为0电平（开通时刻）与Vds4由0电平变为高电平（关断时刻），ILr值几乎为0，因此可知开关管S4的开通与关断均实现了ZCS. 而对于开关管S3，其软开关特性与S4一致，故不再用实验进行说明.

图15（c）为超前桥臂开关管S1的驱动电压Vgs1与漏源电压Vds1波形，可见在Vgs1驱动为高电平前，Vds1已降低到0，因此S1实现了ZVS. 而对于开关管S2，其软开关特性与S1一致，故不再用实验进行说明.

图16展示了变换器在Vin = 380 V，Vout = 300 V下的效率测试曲线，可见变换器满载效率可达94.57%，半载效率仍达90.7%.

5   结   论

本文针对传统移相全桥变换器轻载ZVS性丢失以及副边侧二极管反向恢复严重等问题，提出了一种新型的ZV-ZCS型移相全桥变换器，以提升变换器工作性能. 该变换器在重载时全部开关管开通实现ZVS，在轻载时超前桥臂开关管开通ZVS，滞后桥臂开通与关断实现ZCS，副边二极管实现ZCS. 本文对该变换器工作原理和模态进行了详细阐述，建立了该拓扑CCM与DCM下的增益表达式，并给出了主要参数的设计准则. 通过PSIM仿真验证了不同工况下的工作模态、ZV-ZCS区域和占空比D与理论分析的一致性. 最后搭建了一个2 kW的实验样机，实验结果证明了该拓扑的可行性与理论分析的正确性.

参考文献

[1]    WANG C M，LIN C H，LIN H Y. High-efficiency and low-stress ZVS-PWM bidirectional DC/DC converter for battery charger [C]// 2011 6th IEEE Conference on Industrial Electronics and Applications. Beijing：IEEE，2011：1185—1190.

[2]    孙凯，陈欢，吴红飞. 面向储能系统应用的隔离型双向DC-DC变换器分析方法与控制技术综述[J]. 电工电能新技术，2019，38（8）：1—9.

SUN K，CHEN H，WU H F. A review of analysis method and control technology for isolated bidirectional DC-DC converter used in energy storage systems[J]. Advanced Technology of Electrical Engineering and Energy，2019，38（8）：1—9. （In Chinese）

[3]    王勇.电动汽车充电系统及其控制器的研究[D]. 北京：华北电力大学，2009：1—4.

WANG Y. Research to the charge system and its controller for electric vehicles[D]. Beijing：North China Electric Power University，2009：1—4. （In Chinese）

[4]    宋永華，阳岳希，胡泽春. 电动汽车电池的现状及发展趋势[J].电网技术，2011，35（4）：1—7.

SONG Y H，YANG Y X，HU Z C. Present status and development trend of batteries for electric vehicles[J]. Power System Technology，2011，35（4）：1—7. （In Chinese）

[5]    朱建华，罗方林. 功率谐振变换器及其发展方向[J]. 电工电能新技术，2004，23（1）：55—59.

ZHU J H，LUO F L. Power resonant converter and its development trend[J]. Advanced Technology of Electrical Engineering and Energy，2004，23（1）：55—59. （In Chinese）

[6]    方宇，徐德鸿，张艳军. 高功率密度LLC谐振变换器的研究[J].电力电子技术，2007，41（8）：16—18.

FANG Y，XU D H，ZHANG Y J. Design of high power density LLC resonant converter with extra wide input range[J]. Power Electronics，2007，41（8）：16—18. （In Chinese）

[7]    KIM C E. Optimal dead-time control scheme for extended ZVS range and burst-mode operation of phase-shift full-bridge （PSFB） converter at very light load[J]. IEEE Transactions on Power Electronics，2019，34（11）：10823—10832.

[8]    李景新，牛利勇，王健强，等. 一种提高电动汽车充电机轻载运行效率的方法[J]. 电工电能新技术，2010，29（3）：35—38.

LI J X，NIU L Y，WANG J Q，et al. An approach to improve efficiency of EV charger under light load[J]. Advanced Technology of Electrical Engineering and Energy，2010，29（3）：35—38. （In Chinese）

[9]    李琳. 带箝位二极管移相全桥（PSFB）变换器整流二極管振荡研究[J]. 电子设计工程，2014，22（2）：91—94.

LI L. Research of PSFB converter with clamping diodes and rectifier diode oscillation[J]. Electronic Design Engineering，2014，22（2）：91—94. （In Chinese）

[10]  何德威，石春，吴刚. 数控电源整流二极管换流振荡分析与抑制[J]. 电子技术应用，2019，45（4）：135—138.

HE D W，SHI C，WU G. Analysis and suppression on rectifier diode of outside of oscillation of digital controlled source[J]. Application of Electronic Technique，2019，45（4）：135—138. （In Chinese）

[11]  李剑，康勇，孟宇，等. 带饱和电感的移相全桥零电压开关PWM变换器[J]. 电力电子技术，2000，34（2）：13—15.

LI J，KANG Y，MENG Y，et al. Application of a PS-FB-ZVS-PWM converter with saturable inductor[J]. Power Electronics，2000，34（2）：13—15. （In Chinese）

[12]  杜军，周雒维，陆治国. 带饱和电感的移相全桥PWM变换器软开关分析[J]. 重庆大学学报（自然科学版），2004，27（1）：53—57.

DU J，ZHOU L W，LU Z G. Soft-switching analysis of phase-shifted-FB-ZVS-PWM DC-DC converter with saturable inductor[J]. Journal of Chongqing University （Natural Science Edition），2004，27（1）：53—57. （In Chinese）

[13]  张沛然，李敏远. 一种加辅助网络的移相全桥ZVS PWM变换器[J]. 电力电子技术，2013，47（2）：67—69.

ZHANG P R，LI M Y. A novel phase-shifted full-bridge ZVS PWM converter employing an auxiliary net[J]. Power Electronics，2013，47（2）：67—69. （In Chinese）

[14]  史良辰.滞后臂并联辅助电路移相全桥ZVS变换器的研究[D].南京：南京航空航天大学，2013：15—16.

SHI L C. Research on phase-shift full-bridge ZVS converter with auxiliary circuit for lagging-leg[D]. Nanjing：Nanjing University of Aeronautics and Astronautics，2013：15—16. （In Chinese）

[15]  侯聪玲，吴捷. 3 kW移相全桥变换器ZVS的研究[J]. 电力电子技术，2014，48（5）：65—67.

HOU C L，WU J. Study of 3 kW phase-shift full-bridge converter ZVS[J]. Power Electronics，2014，48（5）：65—67. （In Chinese）

[16]  任晓丹，尹强，庞浩，等. 频率可调移相全桥ZVS变换器的应用研究[J]. 电器与能效管理技术，2015（16）：47—51.

REN X D，YIN Q，PANG H，et al. Research of phase-shift full-bridge ZVS converter with adjustable frequency[J]. Electrical & Energy Management Technology，2015（16）：47—51. （In Chinese）

[17]  ZHAO L，LI H Y，WU X，et al. An improved phase-shifted full-bridge converter with wide-range ZVS and reduced filter requirement[J]. IEEE Transactions on Industrial Electronics，2018，65（3）：2167—2176.

[18]  TENG J H，LIU B H. Three-stage dead-time adjustment scheme for conversion efficiency enhancement of phase-shift full-bridge converters at light loads[J]. IEEE Transactions on Industrial Electronics，2021，68（2）：1210—1219.

[19]  WANG H，SHANG M，KHALIGH A. A PSFB-based integrated PEV onboard charger with extended ZVS range and zero duty cycle loss[J]. IEEE Transactions on Industry Applications，2017，53（1）：585—595.

[20]  RIEDEL J，HOLMES D G，MCGRATH B P，et al. Maintaining Continuous ZVS operation of a dual active bridge by reduced coupling transformers[J]. IEEE Transactions on Industrial Electronics，2018，65（12）：9438—9448.

[21]  KHERALUWALA M N，GASCOIGNE R W，DIVAN D M，et al. Performance characterization of a high-power dual active bridge DC-to-DC converter[J]. IEEE Transactions on Industry Applications，1992，28（6）：1294—1301.

[22]  INOUE S，AKAGI H. A bidirectional DC-DC converter for an energy storage system with galvanic isolation[J]. IEEE Transactions on Power Electronics，2007，22（6）：2299—2306.

[23]  DENG J Y，WANG H Y. A hybrid-bridge and hybrid modulation-based dual-active-bridge converter adapted to wide voltage range[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics，2021，9（1）：910—920.

[24]  BHATTACHARJEE A K，BATARSEH I. Optimum hybrid modulation for improvement of efficiency over wide operating range for triple-phase-shift dual-active-bridge converter[J]. IEEE Transactions on Power Electronics，2020，35（5）：4804—4818.

[25]  YAN Y，GUI H D，BAI H. Complete ZVS analysis in dual active bridge[J]. IEEE Transactions on Power Electronics，2021，36（2）：1247—1252.

[26]  CHEN Z，LI M N，WANG Y. Wide-range ZVS phase-shifted full-bridge converter with low circulation loss[C]// IECON 2014 40th Annual Conference of the IEEE Industrial Electronics Society. Dallas，TX，USA：IEEE，2014：1882—1888.

[27]  ZHANG J M，ZHANG F，XIE X G，et al. A novel ZVS DC/DC converter for high power applications[J]. IEEE Transactions on Power Electronics，2004，19（2）：420—429.

[28]  MISHIMA T，AKAMATSU K，NAKAOKA M. A high frequency-link secondary-side phase-shifted full-range soft-switching PWM DC-DC converter with ZCS active rectifier for EV battery chargers[J]. IEEE Transactions on Power Electronics，2013，28（12）：5758—5773.

[29]  电动汽车充电设备检验试验规范：第1部分 非车载充电：NB/T 33008.1—2018[S]. 北京：中国电力出版社，2018：8.

Inspection and test specifications for electric vehicle charging equipment：part 1 off-board charger：NB/T 33008.1—2018[S]. Beijing：China Electric Power Press，2018：8. （In Chinese）

摘   要：为解决传统DC/DC移相全桥变换器轻载零电压开通（Zero-Voltage Switching，ZVS）性能丢失与副边侧二极管严重的反向恢复问题，本文通过将传统DC/DC移相全桥变换器副边侧的滤波电感前移至原边侧，实现重载下原边侧全部开关管的ZVS特性，轻载下滞后桥臂开关管的零电流开通与关断（Zero-Current Switching，ZCS）特性. 该拓扑可实现副边二极管的电流在重载下自然过零，轻载下进入电流断续模式（Discontinuous Conduction Mode，DCM），有效削弱二极管反向恢复问题. 通过对该拓扑电流连续模式（Continuous Conduction Mode，CCM）与DCM模式进行详细分述，阐明ZV-ZCS特性的实现机理，通过建立该拓扑不同模式下的增益方程，推导关键参数的设计法则，最后通过PSIM仿真与2 kW的实验样机验证了该拓扑的性能与理论分析的正确性.

关键词：直流变换器;移相全桥;零电压开通;零电流关断

中图分类号：TM46                            文献标志码：A

Topology and Design of ZV-ZCS

DC/DC Phase-shifted Full-bridge Converter

CHEN Zhongwei1，2，LI Kui3，CHENG Yijie4，WANG Hongliang3，LENG Yang1，2，LIU Haotian1，2

（1. Limited Economic & Technical Research Institute，State Grid Hunan Electric Power Company，Changsha 410004，China;

2. Hunan Key Laboratory of Energy Internet Supply-Demand and Operation，

State Grid Hunan Electric Power Company，Changsha 410004，China;

3. College of Electrical and Information Engineering，Hunan University，Changsha 410082，China;

4. Changsha Power Supply Company，State Grid Hunan Electric Power Company，Changsha 410007，China ）

Abstract：To solve the loss of zero-voltage switching （ZVS） performance of traditional DC/DC phase-shifted full-bridge converters under light load and the serious reverse recovery problems of the secondary diodes，in this paper，by moving the filter inductor on the secondary side of the traditional DC/DC phase-shifted full-bridge converter to the primary side，the zero-voltage switching （ZVS） performance of all the switches in the primary-side under heavy load is achieved，and the zero-current switching （ZCS） performance of switches in the lagging bridge can be achieved under light load. In addition，the current of the secondary-side diodes obtains natural zero-crossing characteristics under heavy load and enters in discontinuous conduction mode （DCM） under light load，which effectively weakens the diode reverse recovery problem. Continuous conduction mode （CCM） and DCM of the topology are described in detail，and the realization mechanism of ZV-ZCS characteristics is clarified. By establishing the gain equations in different modes of the topology，the design rules of key parameters are inferred. Finally，simulation based on PSIM software and a 2 kW experiment prototype are developed to verify the characteristic of the topology and the correctness of the theoretical analysis.

Key words：DC-DC converters;phase-shifted full-bridge;zero voltage switching;zero current switching

收稿日期：2020-09-22

基金項目：国家重点研发计划政府间国际科技创新合作重点专项资助项目（2018YFE0125300），International Science and Technology Cooperation Program of China under Grant（2018YFE0125300）;湖南省科技创新平台与人才计划资助项目（2019TP1053），Science-Technology Innovation Platform and Talents Program of Hunan Province（2019TP1053）

作者简介：陈仲伟（1984—），男，湖南长沙人，国网湖南省电力有限公司正高级工程师

通信联系人，E-mail：583297819@qq.com