下肢康复外骨骼人机耦合动力学建模与控制*

张佳俊 张舒 徐鉴

（同济大学航空航天与力学学院，上海200092）

引言

脑卒中、脊椎损伤、偏瘫等疾病，会使得患者部分或完全丧失运动能力，造成肢体残疾.而通过一定的康复治疗手段［1］，则有可能逐渐恢复其运动能力，提高患者的生活质量.但是，由于传统康复治疗需消耗大量人力物力，康复治疗师和康复训练设备资源不足，很大一部分肢体残疾患者无法接受传统康复训练的治疗［2］.而康复外骨骼机器人的出现，则为康复领域带来了新的可能［3］.相比传统康复设备，康复外骨骼具有灵活性强、训练效率高、患者情况监测更加全面的等优点［4］，可加速患者的康复过程，减轻治疗师的负担，未来有望部分或完全取代传统康复设备.

当前，国际上已有部分康复外骨骼投入了市场应用.如日本筑波大学开发的HAL系列［5］，是世界上第一款商业化的外骨骼产品；以色列针对脊椎损伤患者开发的ReWalk［6］；美国范德堡大学开发的Indego外骨骼［7］，在其内部集成了摔倒检测和应对机制；新西兰 Rex Bionics公司开发的 Rex系列［8］，是目前唯一一款无需拐杖或支撑架等外部辅助的外骨骼.而国内的康复外骨骼研究则起步较晚，但也取得了一定的成果，如中科院先进技术研究院开发的康复下肢外骨骼［9］，电子科技大学开发的下肢助力外骨骼等［10］，此外，浙江大学、哈尔滨工业大学等众多高校和研究机构也在外骨骼领域展开了许多研究［11］.而市场方面，傅立叶智能科技公司开发的ExoMotus系列下肢康复外骨骼，目前已正式投入商业化运营.总体来说，康复外骨骼领域近年来取得了阶段性的进展，但许多制约其发展的关键性问题，如成本、能源、稳定性、人机协同等，仍有待深入研究.其中，设计安全可靠的人机协同控制策略，在康复外骨骼的研究中占据着基础性的地位［12］.

在康复外骨骼的控制中，直接的控制对象是外骨骼本身，但最终目的是服务患者.因此，在设计控制策略时必须考虑患者与外骨骼的交互.患者与外骨骼的交互主要集中在两个层面，物理交互以及认知交互［13］.从不同交互层面中识别患者的运动意图，进而设计相应的控制策略，是实现患者与外骨骼协同控制的基础［14］.根据患者运动意图的获取方式不同，考虑人机交互的患者-外骨骼协同控制策略可分为以下两类：

第一类，基于认知交互的控制策略，即从认知交互层面获取患者主动意图，多数做法为，将行走过程中患者的EEG（脑电信号）或EMG（肌电信号）通过一定的处理方式转化为患者的主动意图［15］，进而确定外骨骼的跟踪目标，如HAL系列外骨骼，均采用此类控制策略.由于患者的运动意图产生于实际运动发生之前［16］，因此基于认知交互的控制策略在原理上可有效避免患者于外骨骼之间产生过大的交互力，但难点在于如何从复杂且不确定性很高的EEG或EMG信号中获取患者的主动意图［17］.

第二类，基于物理交互的控制策略，即通过患者与外骨骼之间的交互力来获取患者的运动意图［18］，最常用的有力位混合控制、阻抗控制、导纳控制以及滑模控制等［19］.基于物理交互的患者运动意图获取要滞后于认知交互，但其稳定性要高于基于认知交互的意图识别.

基于物理交互的患者主动意图识别，其核心在于患者于外骨骼之间的人机交互力.准确把握人机交互力的动力学特性，对于患者与外骨骼的协同控制以及外骨骼的性能评价具有重要的意义.但鉴于其在运动过程中表现出的复杂性，这一领域的研究仍处于起步阶段［20］.因此，有必要对其进行动力学建模.然而，单纯的人体或外骨骼动力学模型，无法完整体现人机交互力的“交互行为”.故本文认为，有必要建立人体与外骨骼耦合的动力学模型，将人体和外骨骼的对交互力的影响均考虑在内，对其作相关的分析.

本工作以下肢康复外骨骼机器人为研究对象，将患者的对外骨骼的影响考虑在内，并对人机交互力和地面接触力进行建模，建立人体与外骨骼耦合的动力学模型.进一步，在耦合模型的基础上，根据康复训练的不同阶段，设计相应的控制策略：在被动康复阶段，采用传统的PID控制策略，并对交互力作出分析，以期对外骨骼的物理交互设计提供参考；在主动康复阶段，采用阻抗PID控制，将患者的运动意图考虑在内，以降低人机交互力.

1 人机耦合动力学模型

在康复治疗的过程中，患者和外骨骼在物理上存在着复杂的耦合行为，这一行为集中体现在人机交互力上.有效地分析人机交互的动力学特性，对于准确评估患者的恢复情况、舒适度以及外骨骼的性能等，起着重要的作用.而单纯的外骨骼或者人体的动力学模型，无法有效体现患者与外骨骼之间的交互行为.因此，建立考虑人机耦合行为的动力学模型是必要的.

1.1 运动学模型

首先，为简化问题，做出以下假设：由于正常人行走时的运动主要发生在矢状面内，因此仅保留系统在矢状面内的运动；假设人体的左右腿完全对称；假设人体和外骨骼下肢对应的几何长度相等.基于以上假设，将人体和外骨骼均简化成七根匀质连杆组成的平面系统，其中躯干及以上的上半身部位简化成一根杆，整个系统由这两个子系统构成.

在人体上定义9个广义坐标：qH={xH，yH，θHu，1，θHl，1，θHl，2，θHl，3，θHr，1，θHr，2，θHr，3}T，分 别表示髋关节点的位移、上半身的转角、左右髋膝踝六个关节的转角，所有转角的零点均取为人在直立站姿时的位置，且均以逆时针方向为正向，同时，角度下标中的第一个用于区分人体和外骨骼，第二个用于区分上肢以及左右侧，第三个用于标记同侧的不同关节；同时，由于人在行走过程中，踝关节可近似视为被动关节［21］，因此，本文在踝关节上添加了刚度和阻尼均为常数的扭簧.而需要说明的是，目前发展的较为成熟的外骨骼，踝关节也大多为被动关节.综上，以同样的处理方式，定义外骨骼的9个广义坐标：qR={xR，yR，θRu，1，θRl，1，θRl，2，θRl，3，θRr，1，θRr，2，θRr，3}T，整个人机耦合系统的模型如图1所示.另一方面，本文不考虑人体足底和外骨骼的交互力，假设人体和外骨骼的足底完全重合.为简化运动学分析，通过在系统上添加以下理想约束来实现

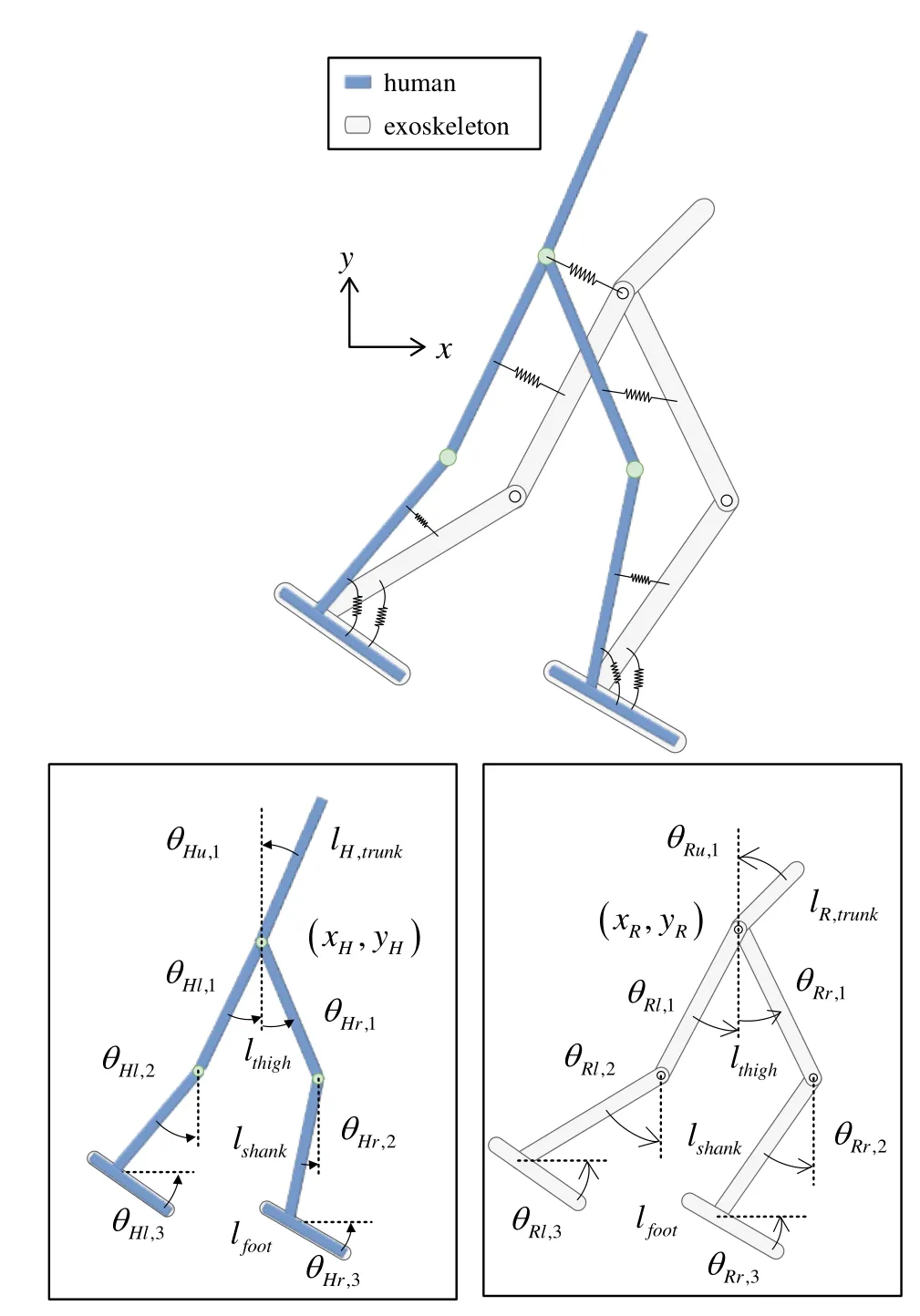
图1 人机耦合模型示意图Fig.1 Sketch map of human-machine coupling model

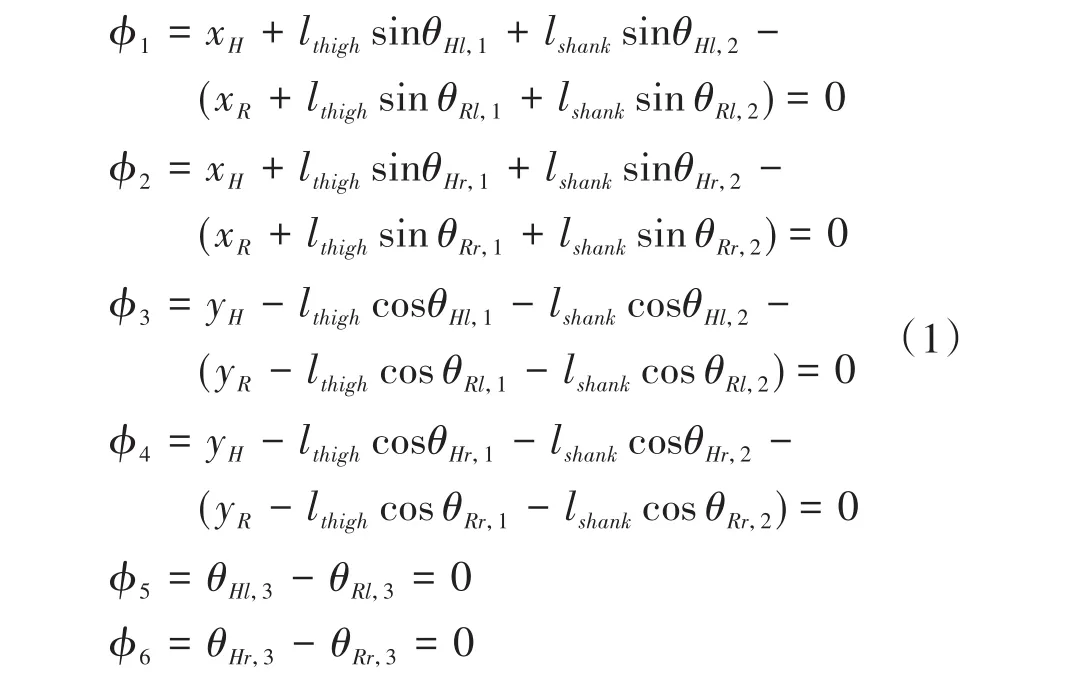
其中，φ1、φ2、φ3、φ4分别约束了人体和外骨骼左右脚上踝关节点的x和y坐标对应相等，φ5和φ6则约束了左右踝关节的转角对应相等.lthigh和lshank分别为大腿和小腿的几何长度.

1.2 足底-地面接触力模型

行走过程中，地面对于系统的约束为单边约束，且在足底与地面接触的过程中会发生碰撞行为，数学上难以处理.本文将地面近似成弹簧阻尼系统，建立足底与地面交互的接触力模型.系统与地面的交互力主要为足底与地面之间的压力和摩擦力.为简化问题，本文假设仅脚尖和脚跟两点与地面之间存在法向接触力和摩擦力.法向接触力可用 Kelvin-Voigt模型［22］给出

其中，i用来标记区分左右脚的脚尖或脚跟，δi为接触深度，可由地面高度yground和脚尖或脚跟的坐标计算得到

kN，i和 cN，i为对应的接触刚度和接触阻尼，对二者进行光滑化处理，得到

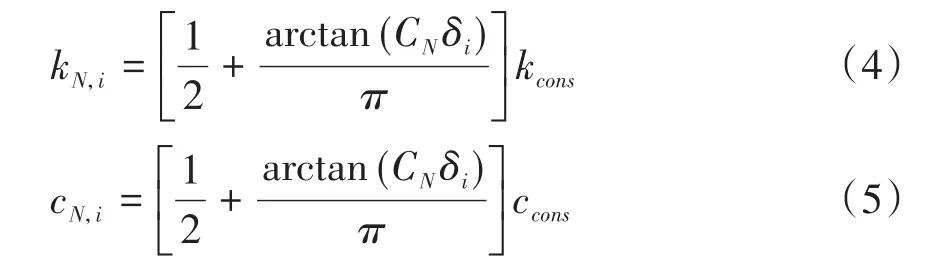
其中，kcons和ccons为给定的常数，CN用于表征接触刚度和接触阻尼光滑化的程度.基于（2）式给出的法向力，采用库伦干摩擦模型描述接触摩擦力，并用相同的手段做光滑化处理

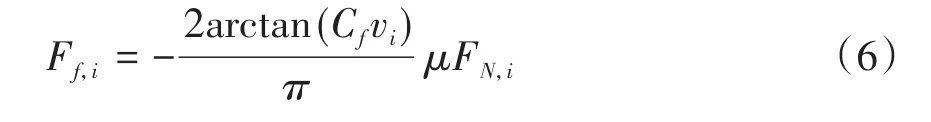
其中，Cf用来表征摩擦力光滑化的程度，vi为接触点的相对速度，μ为动摩擦系数.利用足底-地面接触力作用点的位置对广义坐标的Jacobi矩阵Jc，可得到其作用在广义坐标上的广义力形式

其中，Fcontact表示所有足底-地面接触力的集合.

1.3 人机交互力模型

一般情况下，下肢康复外骨骼和人体的物理交互位置有以下四处：腰部和盆骨附近、大腿处、小腿处、足底.关于足底的交互，本文做出假设，将人体和外骨骼的足底通过位移约束在一起，不考虑此处的交互力.由于实际行走过程中，人体和外骨骼的角度偏差很小，因此，本文在建模过程中，忽略了交互力的纵向部分，并将大腿和小腿上的交互力均简化为作用在关节上的力矩.以大腿为例，忽略沿大腿方向的纵向分量，保留法向分量，并向髋关节点作力系简化，最终得到等效的交互力矩，过程如图2所示.对于大腿和小腿处等效后的交互力矩，采用以下线性的弹簧阻尼模型表达

图2 人机交互力简化过程示意图Fig.2 An illustration of human-machine interaction force and its simplification

其中，i=l，r用来标记左右侧，j=1，2用来标记所处肢体段，θHi，j为患者 i侧 j肢体段的转角，θRi，j为外骨骼对应的肢体转角.对于腰部附近的交互力，仅保留其在患者前进方向上的力分量，交互位置简化到髋关节所在的关节点处，同样用线性的弹簧阻尼模型表达

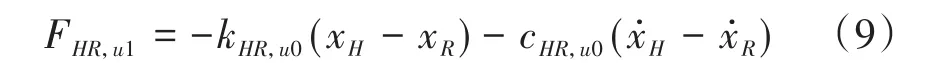
式（8）和式（9）中的刚度 kHR，ij和阻尼cHR，ij均取为常数.上述交互力，可通过其作用位置对应的Jacobi矩阵Jint，计算得到其作用的广义力形式

其中，FHR表示所有人机交互力组成的向量.

1.4 基于第一类拉格朗日方程的动力学建模

结合前文中给出的约束条件、足底地面接触力模型以及人机交互力模型，采用第一类拉格朗日方程［23］建立系统的动力学方程

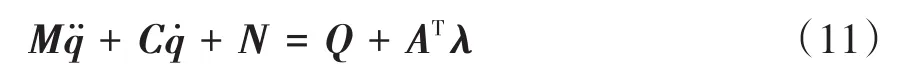
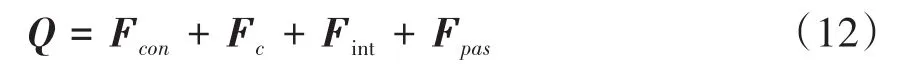
其中，Fcon为外骨骼关节控制力和患者主动力对应的广义力向量；Fc为足底地面接触力对应的广义力向量；Fint为人机交互力对应的广义力向量；Fpas为踝关节上的弹簧阻尼力对应的广义力向量.A为约束矩阵，λ为对应的拉格朗日乘子向量.A可由（1）式中给出的约束条件计算得到

其中，Φ为约束条件组成的向量.

2 分阶段康复控制策略

在康复治疗中，患者会因为运动功能受损情况以及恢复水平的不同而呈现不同的状态，在康复训练中体现出不同的运动能力，而患者所能提供的主动力则是评价其运动能力的重要指标.在患者接受康复训练的过程中，需要根据患者自身的运动功能恢复情况，制定对应的康复训练策略，则康复外骨骼的控制策略也应做出相应的调整.因此，本文依据患者在康复训练中是否提供主动力，将康复训练分为被动阶段和主动阶段，并根据不同阶段患者的需求，制定了不同的外骨骼控制策略.

2.1 被动阶段控制策略

在被动康复阶段，患者几乎不提供主动力，由外骨骼带动整个人机系统运动.并且，为了达到既定的康复效果，此阶段一般要求重复训练指定的步态轨迹.因此，设定此阶段的控制目标为在关节空间中，确保外骨骼以一定精度跟踪预设的目标轨迹.PID控制器由于其原理简单、便于实现且可靠性高的优势，被广泛应用于工业领域的控制中［24］.因此，在康复训练的被动阶段，采用PID控制器来实现外骨骼在关节空间中对于目标轨迹的跟踪.本文的动力学模型中，将踝关节设定为被动关节，因此，仅在外骨骼的左右髋、膝四个关节上施加控制力矩，其具体值由PID控制器给出

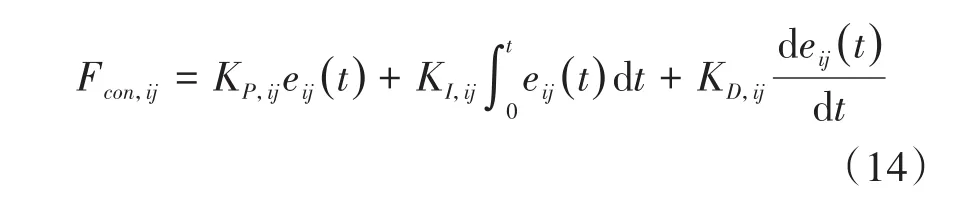
其中，i和j的定义同（8）式，Fcon，i表示外骨骼i侧主动关节 j对应广义坐标上的控制力矩，KP，ij、KI，ij、KD，ij为对应控制器的比例、积分、微分增益.eij(t)为对应关节转角的跟踪误差：

其中，θcRi，j为对应关节上预设的参考轨迹.

2.2 主动阶段控制策略

在主动康复阶段，患者提供一定的主动力，但同时，患者所提供的主动力不足以支撑自身的运动，需要外骨骼提供一定的助力，实现二者的协同运动.在此阶段，外骨骼要保证能够一定程度上跟随患者的运动，以避免因患者自身的运动与外骨骼预设的轨迹产生较大冲突，进而产生过大的人机交互力，对患者造成二次伤害.因此，本文在被动阶段PID控制的基础上，引入阻抗控制［25］，在人机交互力模型的基础上，对（15）式进行修正

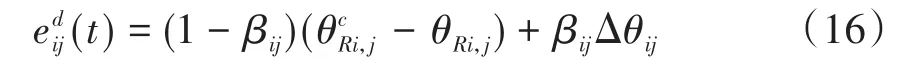
其中，Δθij为阻抗控制器给出的角度修正量，可由人机交互力模型计算得到

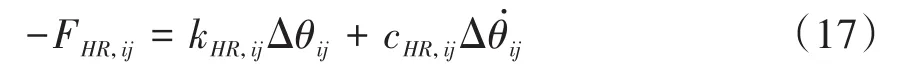
其中

θHi，j为对应人体关节的角度 .βij为 PID 控制器跟踪预定参考轨迹和患者自身运动轨迹的比例系数.对βij取不同的值，会得到不同的效果，其中βij的值越大，参考信号中人体自身运动意图的比例就越大，则人机交互力的水平就越低，但过大的βij值会导致外骨骼的轨迹与其预设参考轨迹有较大的偏差.

区别于一般外骨骼阻抗控制中对于阻抗参数的调控，本文从人机交互力的角度给出了阻抗参数的实际物理意义，即为人机交互力模型中的参数.并通过引入比例系数βij，来具体调控控制器的跟踪信号.此阶段的控制回路如图3所示.

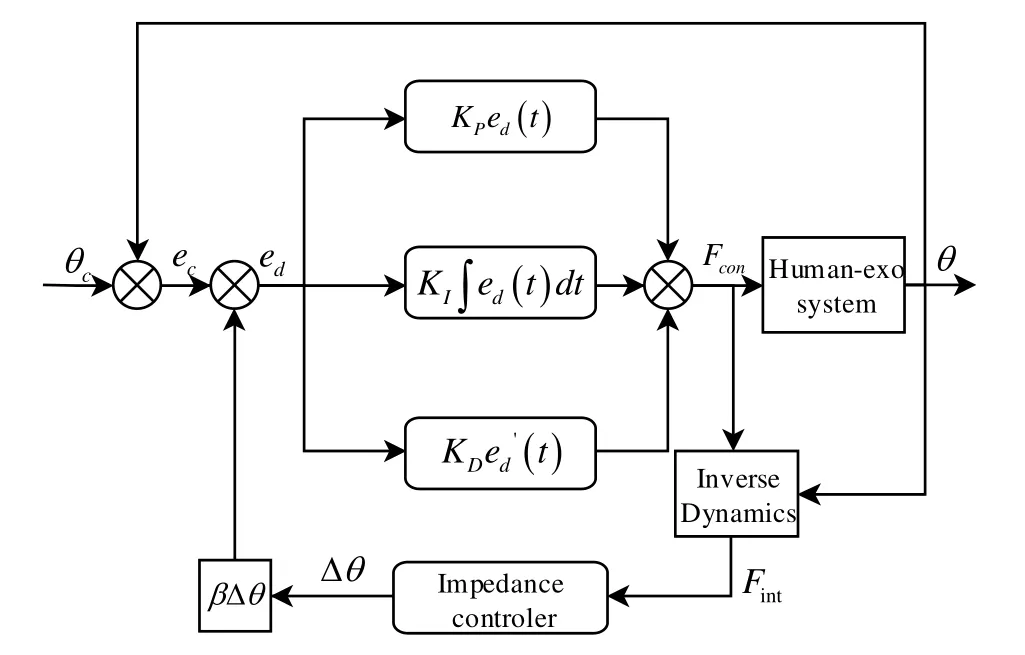
图3 阻抗PID控制器示意图Fig.3 Sketch map of Impedance PID Controller

3 仿真结果

仅在外骨骼的髋关节和膝关节上添加主动力矩，其预设参考轨迹取自健康人行走时的自然步态数据.而本文中所使用的人体自然步态数据均引自文献［26］中的实验数据.所有的仿真均在Matlab中进行，受试者的几何和惯性参数，如表2所示.外骨骼的总体质量参考HAL下肢外骨骼的参数，取为23kg，其中，下肢部分的质量分布参考人体的质量分布，如表3所示.同时，考虑到康复外骨骼的实际动力来源，对外骨骼输出的关节力矩设置一个阈值.对于以下的仿真计算，此阈值均取为500Nm.

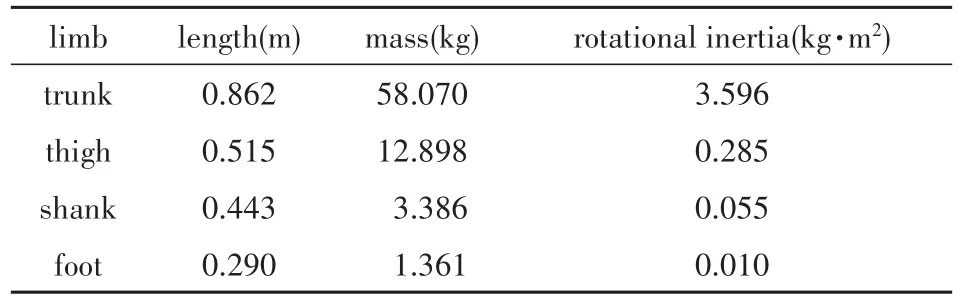
表1 人体几何和惯性参数Table 1 Geometric and inertial parameters of human body

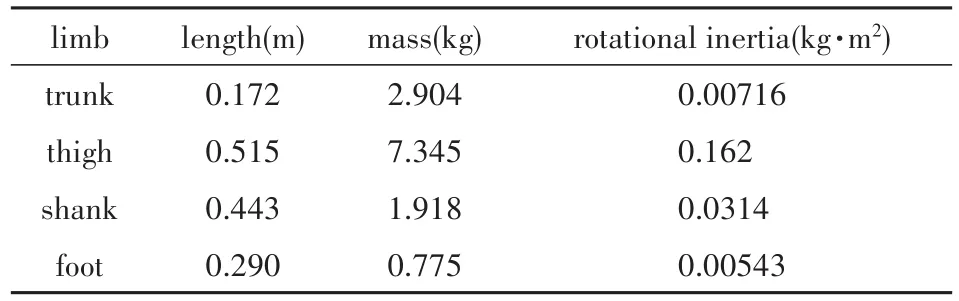
表2 外骨骼几何参数和惯性参数Table 2 Geometric and inertial parameters of exoskeleton

3.1 被动阶段

首先，在特定的人机交互模型参数下，外骨骼及人体各关节在一个步态周期内的轨迹跟踪仿真结果如图4所示，图5则展示了大腿和小腿处的等效人机交互力矩在一个步态周期内的变化情况.因左右腿的跟踪信号仅存在半个周期的相位差，因此，仅给出一侧的仿真结果，将髋关节、大腿处以及小腿处的交互力分别记为FHR，1，FHR，2以及FHR，3.

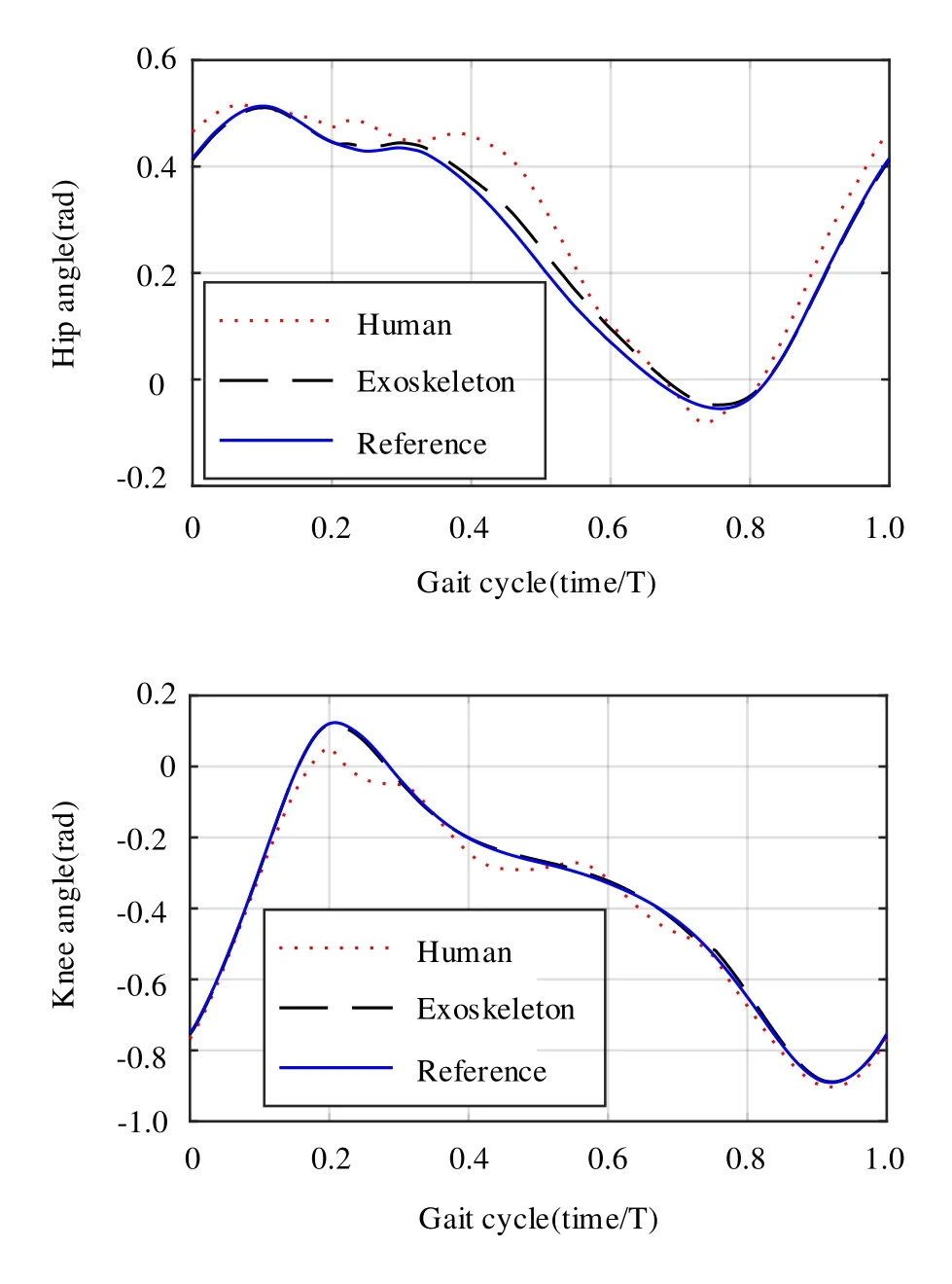
图4 被动阶段主动关节的轨迹跟踪时程图Fig.4 Trajectory tracking diagram of the active joint in the passive stage

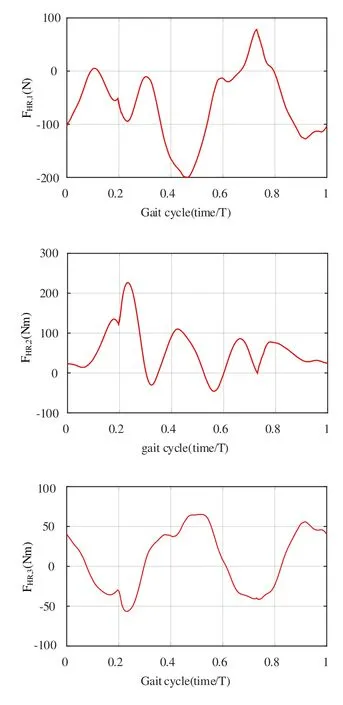
图5 被动阶段系统各处交互力时程图Fig.5 Time-history diagram of the interaction forces in the passive stage

可以看出，外骨骼的各关节对于参考轨迹的跟踪情况良好，而人体关节的轨迹则与参考轨迹存在一定的偏差.此时，主要由人机交互力提供人体行走的主动力，因此，探究人机交互力参数对于人体关节的轨迹跟踪情况及人机交互力的影响.为简化问题，在大腿和小腿处取相同的交互力参数，且固定各处交互力的阻尼参数，仅探究刚度kHR的影响.取等效交互力矩在一个步态周期内的均方根，作为评价交互力水平的指标.仿真结果如图6所示，其中，kHR，1代表髋关节处交互力的刚度值，kHR，2代表大腿和小腿处等效交互力矩的刚度值.

基于图6中的仿真结果，可以看出，在kHR，1不变的情况下，髋关节处交互力均值随着kHR，2增大而降低；大腿处的等效交互力矩均值先迅速增加而后降低，最后趋于平稳；小腿处等效交互力矩的均值则是先将低，后升高，最后缓慢降低.而保持kHR，2不变，对比不同kHR，1取值下的结果，可以看出，髋关节处交互力均值随着kHR，1的增大而增大，而大腿和小腿处的交互力均值则是随着kHR，1的增大而减小，但这种趋势在大腿处的表现相对于小腿处更为明显.

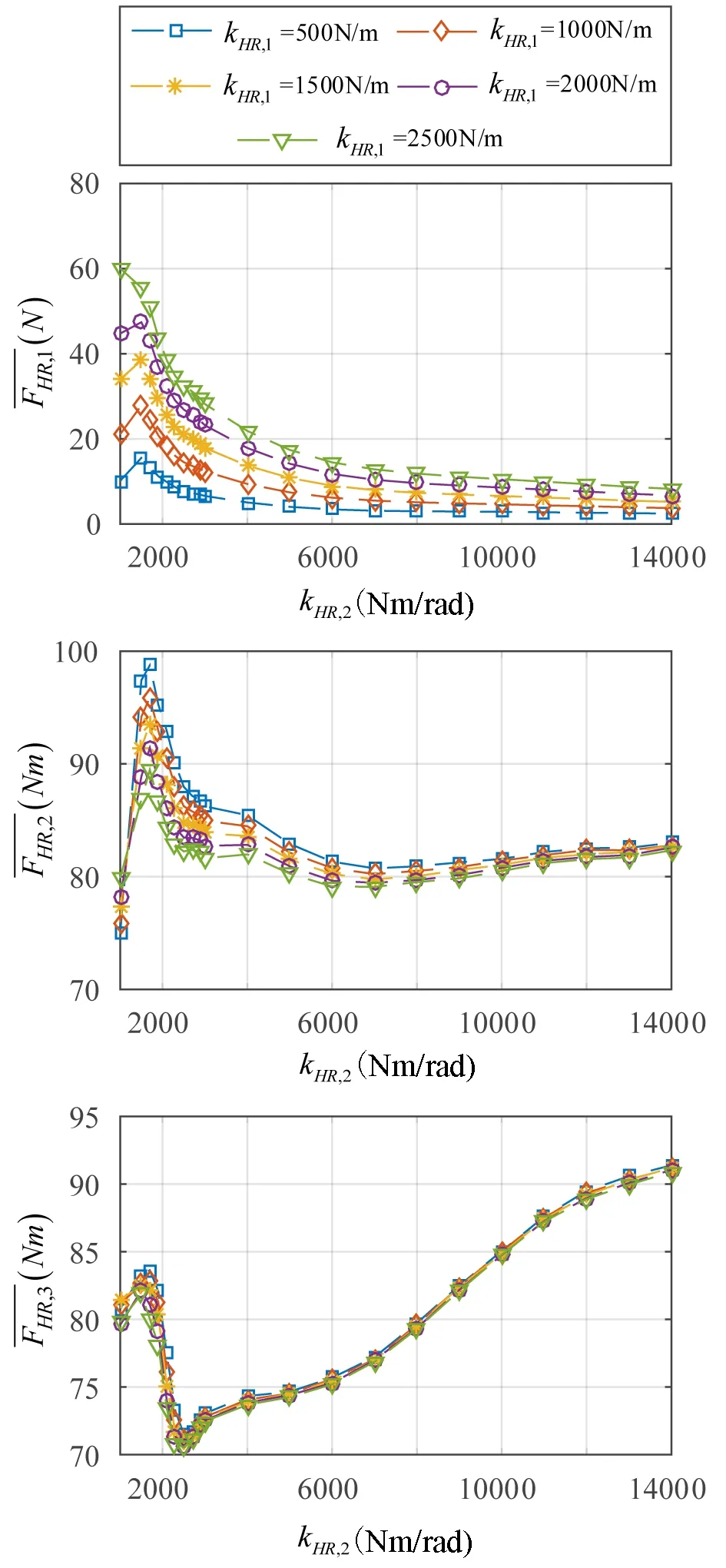
图6 不同交互力刚度取值下的交互力情况Fig.6 Interaction forces with different stiffness values

综合仿真的结果及以上的分析，可以得出：本部分的人体和外骨骼参数及步态数据的情况下，kHR，2选取在5000Nm∕rad左右，会使得大腿和小腿处的交互力矩均处在一个较低的水平.而对于kHR，1的取值，则需要综合考虑髋关节处的交互力和大腿处的等效交互力矩.因此，本文所建的人机耦合模型以及对于人机交互参数的分析，对于外骨骼的参数设计具有一定的参考价值.

3.2 主动阶段

沿用被动阶段关于人机交互力参数的假设，将左右大腿和小腿处的等效人机交互力矩刚度值设为相同，在所给的参考值范围内，取kHR，1为1000N∕m，kHR，2为5000Nm∕rad.为简化问题，人体的主动关节同样取为髋关节和膝关节，且同样通过PID控制的方式给出人体的主动力，但其参考轨迹不同于外骨骼，以此方式在仿真中表现人体不同于外骨骼预设参考轨迹的运动意图.同时，根据前文的控制器设计，仅对大腿和小腿处的等效交互力矩进行调控，并且，为了简化问题，所有的关节上的βij同一时刻均取相同的值β.在不同的步态周期，取不同的β值，对人机交互力进行调控.仿真结果如图7所示.可以看出，在加入了阻抗控制器以后，交互力的整体水平随着步态周期的推进而逐渐降低，实现了预设的效果.且β值越大，交互力的水平降的就越低.

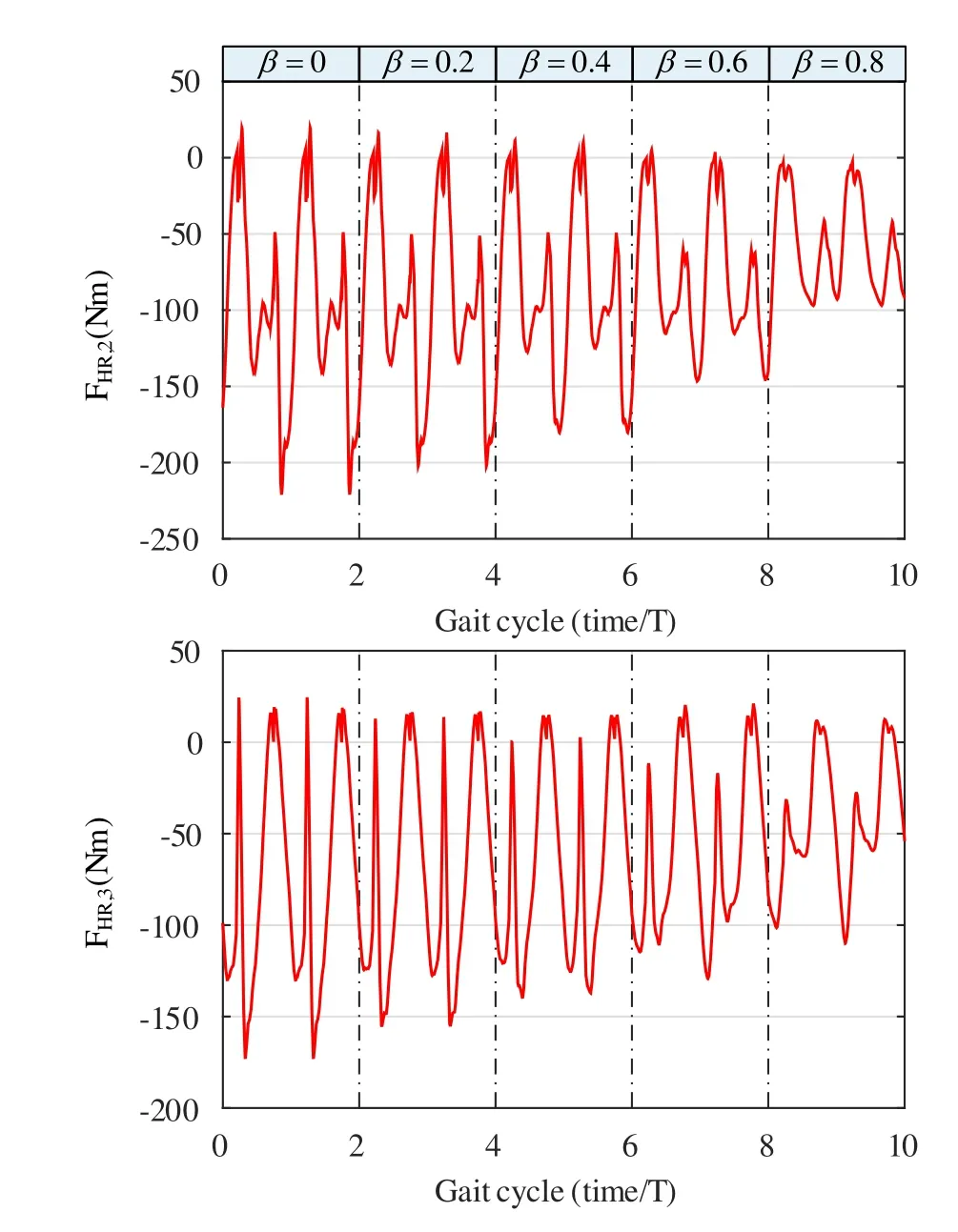
图7 主动阶段人机交互力的调控时程图Fig.7 Time-history diagram of human-machine interaction forces reg⁃ulation in the active stage

4 结论

本文以可穿戴式的下肢康复外骨骼为研究对象，在合理简化的基础之上，综合考虑了足底-地面接触力和人机交互力的影响，采用第一类拉格朗日方程建立了患者与外骨骼相互作用的人机耦合动力学模型.进一步，根据不同康复阶段患者的特点和需求，设计了不同的外骨骼控制策略.最后，通过数值仿真，分析了人机交互力参数的影响，以及所设计控制策略的有效性.主要结论如下：

（1）本文所建立的人机耦合动力学模型，考虑了患者和外骨骼对于人机交互力的共同影响，以及人机交互力的具体分布和形式，对于患者和外骨骼的协同控制有重要的参考意义.

（2）在被动康复阶段，探讨了人机交互力模型中的刚度参数对于人机交互力的影响，对人机交互力的动力学特性做了相应的分析.对于外骨骼的参数设计具有一定的参考价值.

（3）在主动康复阶段，本文设计了阻抗PID控制器，并通过人机耦合的动力学模型，给出了基于交互力的外骨骼阻抗控制中相关参数的实际物理意义.经数值仿真的验证，在患者存在主动力的情况下，所设计的控制策略能够有效地降低人机交互力的水平.

本文从人机耦合的动力学模型出发，对人机交互力做了初步的建模、分析和控制，为基于动力学模型的人体外骨骼协同控制提供了参考依据.后续工作中，将结合实验，进一步对人机交互力模型作分析和辨识，深入研究人机交互力的动力学特性.