参数化列车碰撞平台的动力学建模与仿真*

吴启凡 肖守讷 杨超 朱涛† 阳光武 杨冰

（1.西南交通大学牵引动力国家重点实验室，成都610031）（2.北京交通大学机械与电子控制工程学院，北京100044）

引言

在碰撞事故中，提高车辆的被动安全性至关重要.而验证轨道车辆的被动安全性，可通过实验、仿真等方法进行，考虑到实验场所的有限性以及实验的成本问题，较少采用真车实验的方法.因此在车辆设计过程中，可对车辆进行动力学碰撞仿真［1］.

在列车仿真平台方面，Dias［2］和 Pereira［3］分别建立了一维和二维的简化动力学模型，并通过Abaqus进行计算，对比证明动力学模型的准确性，提出性能良好的时间积分算法可提高动力学模型的计算精度.Milho［4］在建立动力学模型的过程中将车体视为刚体，将吸能防爬装置、车钩缓冲装置等连接部件用非线性模型代替，将其刚度和阻尼特性以力-位移曲线的方式表现.肖守讷［5］的团队基于多体动力学理论建立碰撞动力学耦合模型，研究列车的碰撞响应机理，还对列车整体的能量管理系统进行了研究，表明列车碰撞多体动力学模型能高效快捷地分析不同能量吸收方案的列车碰撞动态行为.田红旗［6］团队运用Matlab、Simpack等软件建立了二维和三维的列车碰撞动力学模型，发现不存在初始横向激励的条件下，列车的垂向平动和点头运动明显，而其他的运动响应较低.由于要进行多次车辆参数的反馈修改，有限元方法建模和计算时间较长.而传统的动力学方法在进行列车碰撞计算的过程中无法表现钩缓装置、吸能防爬装置等非线性部件二次加载卸载的力学特性.

国内外现有的碰撞动力学模型侧重于垂向或纵向的动力学表现，对三维碰撞动力学模型的研究较少.本文尝试使用动力学方法建立参数化仿真平台，基于车辆-轨道耦合动力学理论对车体、转向架以及轨道等部件建立了动力学模型，将车钩缓冲装置、吸能防爬装置等部件简化为数学模型，用非线性迟滞特性曲线表示，从而建立参数化仿真平台.将车辆各部件的质量、转动惯量，吸能、钩缓装置的压溃力、行程等基本参数输入计算，将结果与有限元软件LS-DYNA的结果进行对比，对参数化仿真平台的准确性进行验证.

1 车轨耦合动力学模型

在车轨耦合动力学中，车辆-轨道模型是由实体模型简化而成的数学模型，并且在数学模型中保留了实体模型的重要力学特性.在本文建立的参数化仿真平台中，借鉴了由翟婉明［7］院士提出的车辆-轨道空间耦合模型中的客车动力学模型，如图1所示，本文根据实际碰撞过程中的模型以及各个连接部件之间的关系对原模型进行修改，建立车轨耦合碰撞动力学模型，各参数的含义如表1所示.为了在计算中取得准确性和精度的平衡，在模型的简化和建立过程中，需要遵循以下假设：

表1 模型参数表Table 1 Model parameters

图1 车轨耦合碰撞动力学模型Fig.1 Vehicle-rail coupled collision dynamic model

（1）整个碰撞过程中轮对和平直轨道之间无摩擦，主被动列车在垂向有40mm偏差，横向完全对心，防爬装置正常作用.

（2）车体、构架与轮对为刚体，且质量集中在重心位置.

（3）钩缓装置、吸能防爬装置以及悬挂装置只考虑其等效刚度、阻尼参数.

1.1 车辆模型

如图2所示，车辆模型由7个子部件组成，包括1个车体，2个构架和4个轮对，这些部件全都视作刚体.车体与转向架之间，转向架与轮对之间都通过弹簧阻尼系统连接.其中车体和构架具有完整的6个自由度，即纵向、横向以及垂向平动自由度（x，y，z）和侧滚、点头以及摇头自由度（α，β，γ）；轮对则只有五个自由度（x，y，z，α，γ），即不考虑绕轴向的旋转自由度.所以在车辆模型中一共有38个运动自由度.根据达朗贝尔原理，列出车体、构架以及轮对的受力平衡方程，最终得到38个方程.

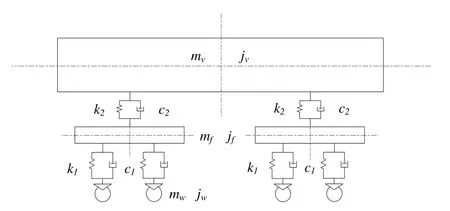
图2 车辆模型Fig.2 Vehicle model

1.2 轨道模型

由于在碰撞过程中，轮轨之间的作用力频率较低，轨道模型对整体计算结果的影响较小，因此基于等效集总参数轨道模型［8］以及弹性离散点支承模型，建立适用于碰撞计算的轨道动力学模型.如图3所示，在此模型中将轨道简化为钢轨、轨枕和地基三个部分，且都视作独立的质量集中刚体，两两之间都通过弹簧、阻尼元件进行连接.在单个车辆-轨道模型中，包含八个钢轨子模型和四个轨枕子模型，且都只有垂向的平动自由度，共有12个运动自由度.

图3 轨道模型Fig.3 Orbit model

与车辆模型类似，根据达朗贝尔原理，列出钢轨和轨枕的受力平衡方程，每个自由度对应一个方程，最终得到12个方程.下面以某一轮对与其对应的轨道为例，列出相应的受力平衡方程.公式（1）包括左侧轨道垂向运动方程、右侧轨道垂向运动方程以及轨枕垂向运动方程.

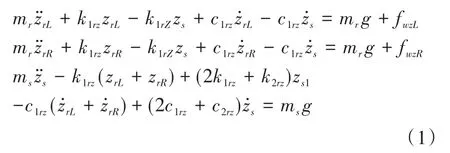
式中，mr为钢轨质量，ms为轨枕质量，k1rz为轨下垫层刚度，k2rz为枕下支撑刚度，c1rz为轨下垫层阻尼，c2rz为枕下支撑阻尼，zrL为左侧轨道垂向位移，zrL为右侧轨道垂向位移，zs为轨枕垂向位移.

2 轮轨接触模型

2.1 Hertz接触理论

车辆模型与轨道模型之间通过轮轨相互作用力［9］连接，而在本文建立的参数化仿真平台中，轮轨作用力计算以Hertz接触理论为基础，轮轨作用力计算公式为：

式中，G为轮轨接触常数，δZ为轮轨间法向压缩量.由公式2不难得出，当轮轨间法向压缩量已知，可计算得出轮轨接触力，进而通过计算轮对与轨道垂向高度差得到轮轨间法向压缩量.

2.2 轮轨相互作用关系

翟婉明［7］提出了一种轮轨空间动态接触模型，该模型考虑了轮对运动过程中分离的情况，将轮对看作弹性体，与实际情况更加符合.王开文［10］提出了一种搜索轮轨接触点的迹线法，使得传统计算比较复杂的接触点搜索转化为求解两条平面曲线之间最短距离的问题，能够有效提升计算效率.在参数化平台碰撞计算的过程中，由于轮轨之间相互作用力远小于车辆相互碰撞力，为了简化模型，提高计算速度，仅考虑轮对在侧滚运动、浮沉运动以及横摆运动，在参数化平台中，采用较为简化的向量法［11］进行计算.

根据实际情况，选用锥型踏面和每延米50kg的钢轨参数进行建模，轨底坡为1：20.轮轨接触示意图如图4所示，在轮对上，接触区为从轮缘内侧往外，即图中从左往右48～ 100mm的区域，此段踏面廓形为1：20；而对于钢轨来说，接触区为钢轨中心面往两侧23mm的区域，总计46mm.

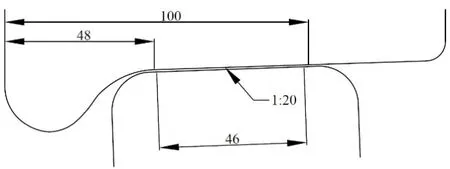
图4 轮轨接触廓形Fig.4 Wheel-rail contact profile

由于车辆名义滚动圆半径以及其到轮对质心的距离已知，初始时刻轮对的横向、垂向位移等参数也是已知的，根据向量法计算公式3，即可得到轮轨间法向压缩量 Δn（L，R），代入公式 4，得到轮轨间作用力 fw（L，R）.向量法相关计算公式如下式所示：

式中，zw为车轮垂向位移，zr为轨道垂向位移，dww为左右轮滚动圆横向距离一半，α为轮对侧滚角，δw为车轮踏面接触角，G为轮轨接触常数.

3 非线性连接模型

3.1 钩缓装置模型

在碰撞发生时，车钩缓冲装置是首先发生能量转换的部件.钩缓装置中起主要作用的是缓冲器和压溃管.因此，钩缓装置模型主要是对缓冲器和压溃管力学特性进行简化后的数学模型.Cole［12］提出了一种非线性迟滞特性数学模型，对车钩缓冲装置进行模拟，将车钩与车体之间的连接结构简化为一根线性弹簧，通过分段线性的方程表达缓冲器中摩擦斜楔的加载特性，最终得到车钩缓冲装置的力-位移曲线.

本文基于车钩缓冲装置分级吸能行为，将其集成为非线性迟滞元件，包括缓冲器曲线和压溃管曲线.如图5所示，实线为加载，虚线为卸载，表示碰撞过程中钩缓装置中缓冲器和压溃管的加卸载过程，包括二次加载、卸载的情况.

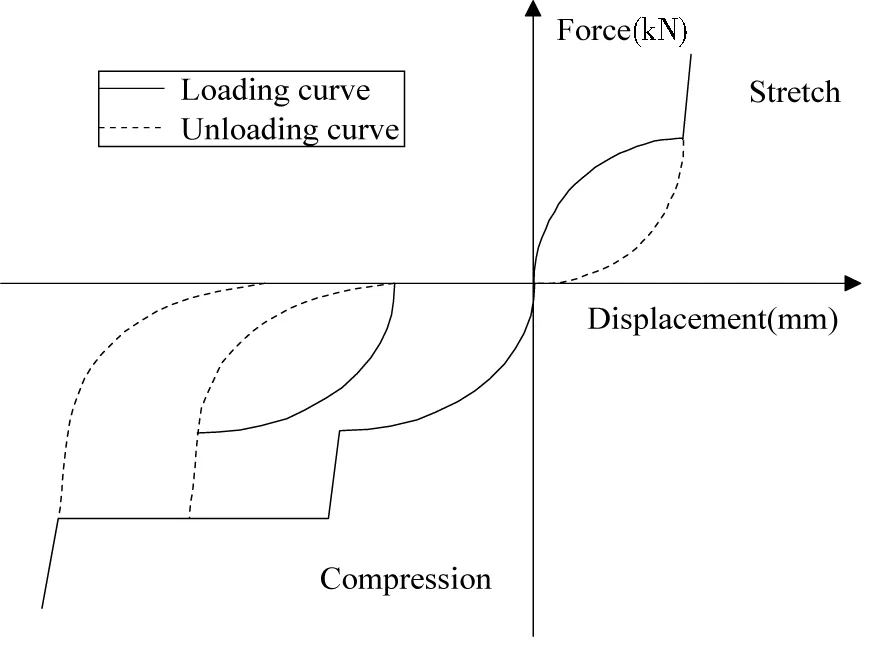
图5 钩缓装置非线性迟滞特性曲线Fig.5 Non-linear hysteresis characteristic curve of hook buffer device

车钩缓冲装置轴向力fcd计算如公式5所示.

式中，Δlc为钩缓装置相对位移；Δvc为钩缓装置相对速度；fcl（Δlc）为与Δlc有关的钩缓装置加载函数，包括不同条件下缓冲器和压溃管加载的力-位移曲线；fcu（Δlc）为与Δlc有关的钩缓装置卸载函数，包括缓冲器卸载的力-位移曲线，以及记录卸载前压溃管行程的相关变量，以便于二次加载；fcu（fcl，fcu）为与fcl和fcu有关的加、卸载转换过渡函数；fcmax为钩缓装置最大阻抗力，Δlcmax为钩缓装置最大压缩行程，两参数用来判定钩缓装置作用的边界值；ε为一很小的正数，目的是规定加载卸载和过渡的范围.

3.2 吸能防爬装置模型

吸能防爬装置作为车辆碰撞过程中的第二级吸能结构，在碰撞吸收总能量中占比较大，为主要吸能部件，该部件一般配置在头车前端.吸能防爬装置主要由防爬齿、吸能装置以及安装座组成.根据丁叁叁［13］对于吸能防爬装置的相关研究，其力学特性曲线可以等效为纵向力关于纵向变形量的曲线.

类似于车钩缓冲装置，本文在其基础上对吸能防爬装置建立数学模型来模拟其力学特性，并用非线性迟滞特性曲线来表示.如图6所示，钩缓装置失效后，吸能防爬装置的防爬齿啮合，当吸能装置走完行程后进行刚性冲击段；图中还包含了吸能防爬装置卸载后再二次加载的过程.

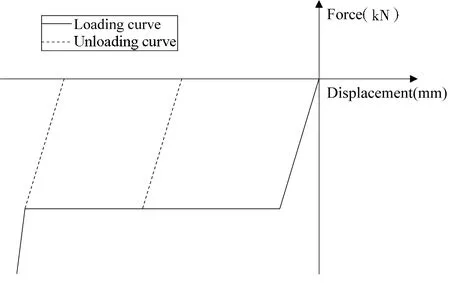
图6 吸能防爬装置非线性迟滞特性曲线Fig.6 Non-linear hysteresis characteristic curve of energy absorbing anti-climbing device

吸能防爬装置轴向力fex计算如公式6所示.

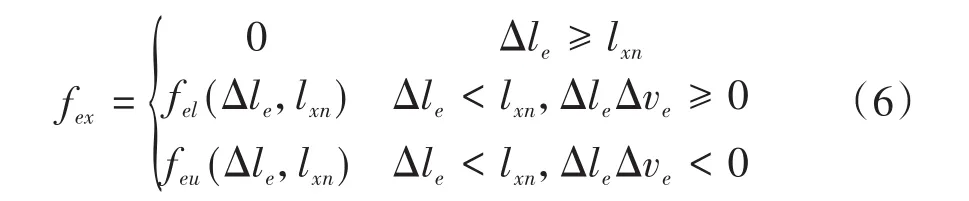
式中，Δle为吸能防爬装置相对位移；Δve为相对速度；fel（Δle，lxn）为与Δle和lxn有关的吸能防爬装置加载函数；feu（Δle，lxn）为与Δle和lxn有关的吸能防爬装置卸载函数；lxn为吸能装置实时压缩行程.

3.3 悬挂装置模型

车辆的悬挂装置包括一系悬挂装置和二系悬挂装置，主要起支撑车体、缓和振动和冲击等作用.根据彭利群［14］的相关实验数据，一系轴箱弹簧的垂向刚度可近似为某定值，而根据李彪［15］和廖英英［16］对悬挂装置的相关研究，空气弹簧可简化为多级刚度和阻尼装置的组合，本文的参数化模型对其进行一定的简化.

当一系弹簧压缩到一定行程后，钢簧到达刚性冲击区，类似地，当一系弹簧拉伸达到一定行程以后，其限位止挡与构架发生接触，出现刚性冲击.当空气弹簧压缩达到极限行程，上下盖板相接触，到达刚性冲击区，当空气弹簧拉伸达到一定行程以后，与二系垂向限位止挡发生接触，出现刚性冲击.通过以上分析可得，集成后的一、二系悬挂装置刚度特性曲线为阶跃函数，如公式7，公式8所示.图7所示为一、二系垂向刚度特性曲线.

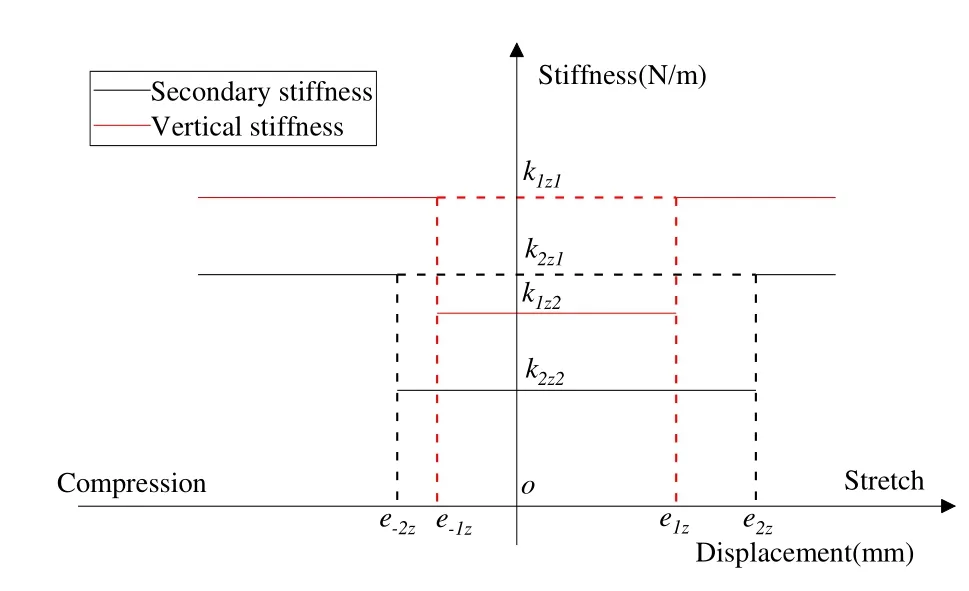
图7 一、二系垂向刚度特性曲线Fig.7 Verticalstiffnesscharacteristicsofoneandtwoserioussuspension

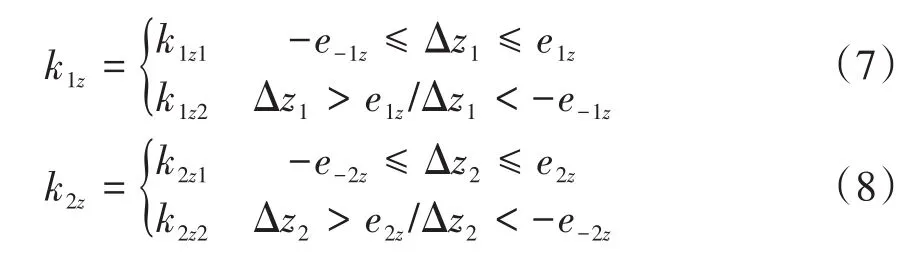
其中，e-1z为一系弹簧压缩间隙；e1z为一系垂向限位止挡间隙；k1z1为一系垂向高度变化量未超过压缩间隙与止挡间隙时的一系弹簧垂向刚度；k1z2产生刚性冲击时的一系弹簧垂向刚度.e-2z为二系弹簧压缩间隙；e2z为二系垂向限位止挡间隙；k2z1为二系垂向高度变化量未超过压缩间隙与止挡间隙时的二系弹簧垂向刚度；k2z2产生刚性冲击时的二系弹簧垂向刚度.

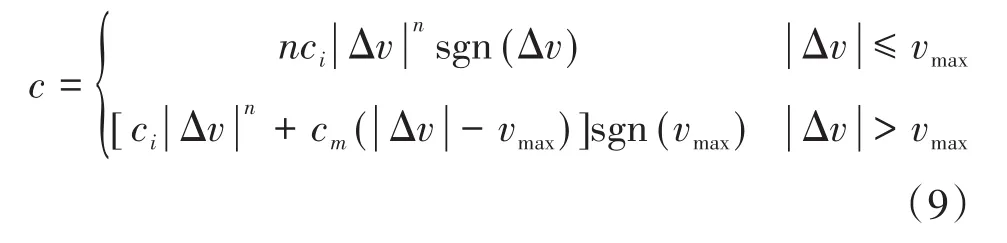
油压减震器为客车转向架常用的减震器，其特性为相对速度越大，阻抗力越大，从而合理匹配减震器两端受到的力［17］.为了模拟油压减震器的力学特性，在参数化平台计算的过程中使用阻尼特性曲线，根据杨超［11］的相关推导，当已知力-速度特性表达式，经过两端求导可得到阻尼特性表达式，如公式9所示，最终得到阻尼特性曲线.如图8所示，vmax为开始卸荷相对速度；cm为卸荷阻尼常数.

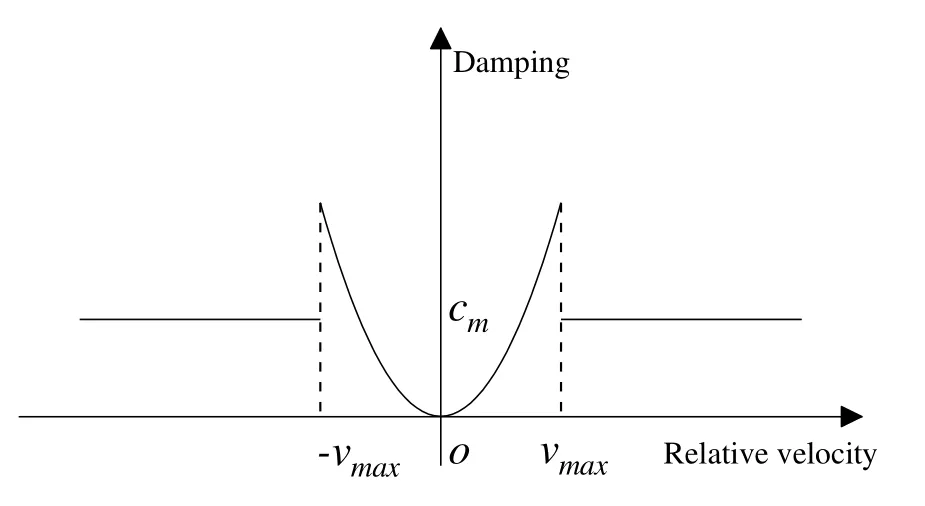
图8 阻尼特性曲线Fig.8 Damping characteristic curve

4 参数化平台的搭建

4.1 迭代算法

单个车辆-轨道模型具有数十个运动自由度，而列车级的碰撞计算，会产生数百个自由度；此外，钩缓装置、吸能防爬装置等部件的数学模型中包含了非线性的力-位移曲线.四阶龙格-库塔法等传统计算方法在计算速度和稳定性方面不能满足要求，杨超［18］提出了一种修正双步长显式法，在解决非线性问题时具有良好的稳定性，在精度和计算速度上取得平衡.其算法公式为：

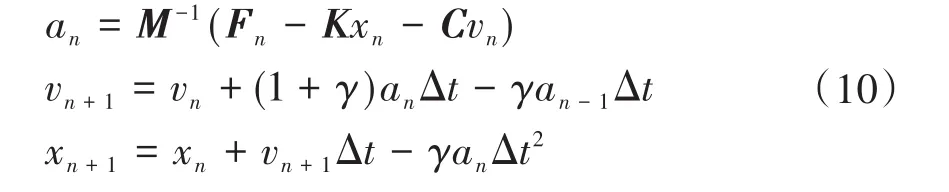
式中，γ为积分参数，用于调整算法精度.此算法在起步计算的时候无需借助其他值，可将0时刻的加速度看作-1时刻的加速度，所以第一步计算只需要输入0时刻的速度和加速度.

4.2 矩阵组装

根据公式（11）中达朗贝尔原理，列出所有物体之间的受力平衡方程，考虑到数量较多的自由度数量以及降低后续的程序编制工作量，将方程组中的各个参数组装成质量矩阵、阻尼矩阵以及刚度矩阵，以车辆轨道碰撞动力学矩阵方程的形式进行计算.在对矩阵进行组装的时候，质量矩阵M、刚度矩阵K、以及阻尼矩阵C，都是按照对角矩阵的形式进行组装，而位移矩阵X和力矩阵F按照列矩阵进行组装.

通过输入列车编组信息、钩缓装置参数、吸能防爬装置参数、悬挂装置参数以及车体参数，即可构造整列车的各型矩阵.矩阵组装完成后，设置时间积分算法的计算总时间，计算时间步长及初始碰撞速度参数，进行计算.整个计算流程如图9所示.

图9 碰撞动力学参数化模型计算流程Fig.9 Calculation process of parametric model of collision dynamics

5 参数化模型的验证

Hypermesh和LS-DYNA是碰撞有限元仿真计算中常用的两个软件，前者用来对三维的车辆模型进行有限元划分，后者进行计算求解.为了验证本文提出的参数化仿真的准确性，本文将参数化模型与有限元仿真进行对比，在对比的过程中设置相同的参数和工况条件，比较计算结果来验证参数化仿真平台的准确性.

计算完成后，基于 EN 15227标准［19］对计算结果进行评价，其耐撞性指标有：轮对抬升量、车体变形量以及平均纵向加减速度等，由于参数化仿真本质上是动力学仿真，无法获得车辆纵向塑性变形的结果，所以，在对比过程中选取最大轮对抬升量、速度以及加速度三项指标进行对比.碰撞模型选用某型四编组列车，主动车以25km∕h的速度，在无摩擦的平直轨道上与一列静止的同类型列车碰撞，两车处于连挂状态，且根据EN 15227的相关规定存在40mm的初始高度差.仿真计算参数表如表2所示，工况示意图如图10所示.

图10 碰撞工况Fig.10 Collision conditions

表2 仿真计算参数表Table 2 Simulation parameters

首先对参数化仿真和有限元仿真的速度结果进行对比，图11为有限元模型的计算结果，图12为参数化模型的计算结果，两种模型的速度变化规律类似.S4界面的头车车钩都在0.25秒左右发生剪断，剪断之后吸能防爬装置开始接触，进行吸能.0.3秒左右，V4车和V5车的速度趋同.最后在0.6秒左右，主动列车和被动列车的各节车速度趋于一个稳定值，整个碰撞过程即将结束.

图11 有限元模型速度结果Fig.11 Velocity results given by finite element model

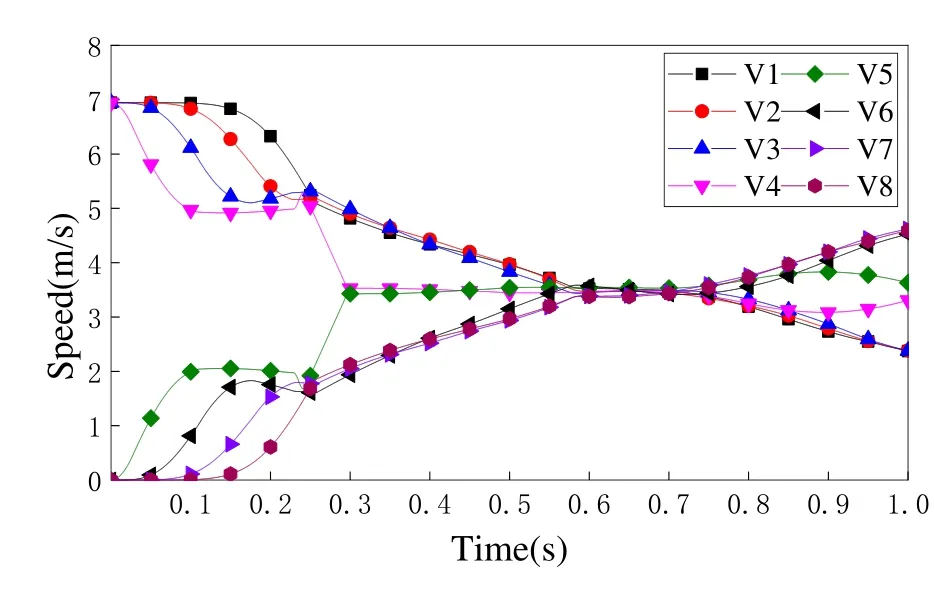
图12 参数化模型速度结果Fig.12 Velocity results given by parametric model

有限元仿真的加速度结果如图13所示，参数化仿真的加速度结果如图14所示.在加速度的变化规律上，两种模型类似，V5车在0.25秒左右出现一个加速度极值.参数化模型和有限元模型的计算结果对于车辆的平均加速度绝对值比较接近，绝对误差小于1m∕s2，相对误差小于5%.

图13 有限元模型加速度结果Fig.13 Acceleration results given by finite element model

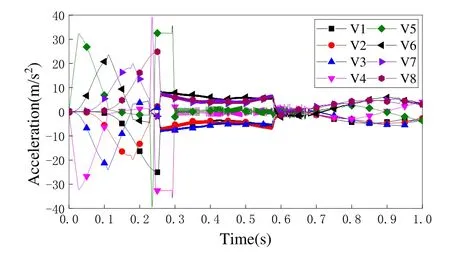
图14 参数化模型加速度结果Fig.14 Acceleration results given by parametric model

图15为两种仿真方法的最大轮对抬升量对比图，由图像可得，两条曲线的变化形势吻合度较好，参数化仿真中轮对抬升量峰值的出现时间比有限元仿真的峰值提前了约0.03秒，而峰值的结果几乎一致，相对误差仅1.67%.考虑到参数化仿真属于多体动力学计算，所有部件视作刚体，相比于有限元仿真，没有弹塑性材料的变形来吸收能量，因此，参数化仿真计算得到的最大轮对抬升量峰值出现的时间略早于有限元仿真的时间.

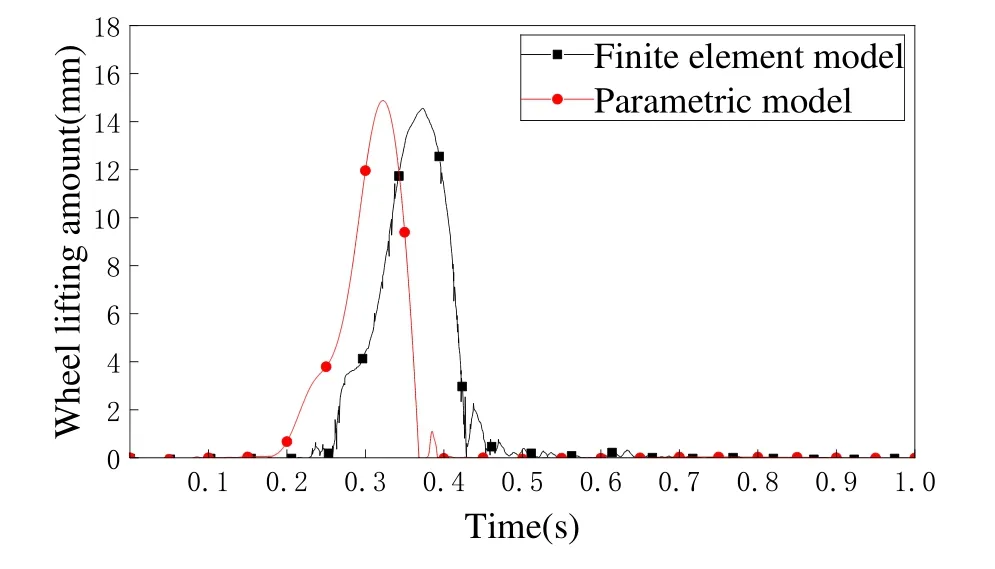
图15 最大轮对抬升量对比Fig.15 Comparison of maximum wheel pair lift

6 结论

本文基于车辆-轨道耦合碰撞动力学理论，构造适用于列车碰撞的车辆参数化模型以及各子系统的数学模型；使用修正双步长显式法对所有参数化模型进行整合，最终建立适用于列车碰撞的参数化仿真平台，选用某型地铁列车进行计算.本文的研究结果包括：

（1）建立了包括车辆模型、轨道模型、轮轨相互作用关系、钩缓装置模型、吸能防爬装置模型以及悬挂系统模型的参数化轨道车辆碰撞模型.轨道模型中考虑了弹性离散点支承结构；基于Hertz接触理论以及向量法建立轮轨相互作用关系；钩缓装置模型考虑了非线性迟滞特性以及碰撞动态激励的影响；吸能防爬装置模型考虑了二次加载以及加卸载转换特性.

（2）将计算结果与有限元软件LS-DYNA进行对比，主、被动车在时域范围内的动态响应趋势与有限元结果类似，两种模型的速度变化趋势、速度交汇时间相对误差保持在5%以内.两种模型的加速度绝对值基本相同，绝对误差小于1m∕s2.

（3）基于欧洲碰撞标准EN15227的相关要求，对碰撞过程中最大轮对抬升量指标进行了对比验证，碰撞过程中最大轮对抬升量峰值相对误差仅1.67%，出现时间相差0.03s，求解结果表明参数化仿真平台的计算结果与有限元结果的一致性较好.

参数化碰撞仿真平台的求解速度快，求解准确性较好，能为轨道车辆的耐撞性设计中参数的选定提供一种较为有效的分析方法，有利于加强轨道车辆的被动安全性.考虑到列车的碰撞是一个集成多种强非线性因素的过程，本文主要研究了列车理想情况下碰撞后的纵向和垂向响应，并与有限元模型进行对比.后续研究中考虑添加横向和垂向激励来更真实地模拟碰撞过程中列车的运行情况，设置完整的边界条件来研究列车碰撞时不同参数产生爬车和脱轨的内在机理.