设有保水堰的有压输水箱涵超设计过流能力研究
2021-09-26李传夫董丹丹何利华
李传夫 董丹丹 何利华
我国水资源分布不平衡,随着经济的发展以及人口日益流动和集中,水资源分布和经济发展不平衡的状况日渐突出。为满足人们的用水需求,解决生产和生活中的用水矛盾,近些年来,各地陆续兴建了一系列长距离引调水工程,长距离输水包括有压流、无压流及有压和无压相结合等3种形式。这些工程极大地缓解了用水短缺的问题,取得了良好的经济效益和社会效益。
近年来,随着地方用水需求逐年增加和工程运行时间的增长,复核引调水工程的过流能力并对其超设计过流能力进行研究,对了解和掌握工程的实际供水能力,并在不突破原设计准则、确保工程安全运行的前提下充分发挥工程潜能、提高输水效益等方面具有重要的意义。
1 项目背景
南水北调中线天津干线工程西起河北省保定市徐水县西黑山村,东至天津市外环河西,全长155.3 km,主要任务是向天津市及天津干线河北省境内部分受水区城市供水。天津干线的设计流量为50~18 m3/s,加大流量为60~28 m3/s。工程采用全箱涵无压接有压全自流输水方案,有压段全长约145 km,分段阶梯状设置8座保水堰井,堰型为实用堰,其作用是保证任何输水工况下两相邻保水堰间的箱涵均为有压流输水状态。工程纵断面示意图如图1所示。

图1 天津干线输水工程纵断面示意图
南水北调中线一期工程天津干线于2014年末进入初期通水运行阶段,截止至2019年末,已通水运行近5年,累计向沿线地区供应水量已超过45亿m3。供水运行过程中,区域的不均匀沉降、建筑物的侵蚀淤积以及水生生物的滋生等因素均会使得箱涵过水断面的性态发生改变,导致其糙率、局部损失系数等发生变化,从而对箱涵过流能力产生影响。
另外,天津干线穿过我国的“千年大计”雄安新区,因天津干线建设早于雄安新区的规划,当时并未考虑新区的用水需求,在国家提出建设雄安新区后,为雄安新区供水,满足新区建设顺利进行的用水需求,在距离雄安新区较近的4#堰附近为新区分水,成了天津干线一个潜在的工程任务。且天津干线受水区对水量的需求逐年增加,在水源地丰水期,有通过有压箱涵向受水区进行超设计能力输水的诉求。因此,有必要对其有压箱涵的过流能力进行复核,并研究其超设计过流的可能性和超设计过流的能力。
2 研究思路
根据恒定流能量方程(见式(1))可知,在过流断面尺寸、来流情况和上下游水位差已知的情况下,有压箱涵过流能力与沿程水头损失和局部水头损失相关。过流时的能量损失越小,过流能力越强;反之,过流时的能量损失越大,则过流能力越差。沿程水头损失和局部水头损失的影响因素分别为过水断面的糙率n和过水结构各处的局部损失系数ζ,见式(2)~(5)。因此,通过测量实际供水流量下的各处水位变化,可以计算出糙率n和局部损失系数ζ,进而可计算天津干线的输水压力水头线,由此可得出天津干线的最大供水能力。
恒定流能量方程:

式中H1、H2两个断面处的水位;
v1、v2——流经两个断面时的流速;
hf、hj——流经两个断面途中的沿程水头损失和局部水头损失;
g——重力加速度。
达西—魏斯巴赫公式:

式中λ——沿程水头损失系数;
L——水流经的距离;
R——水力学半径。

式中C——谢才系数;
谢才系数的经验公式曼宁(R.Manning)公式:

式中n——流道的糙率。

式中ζ——水流的局部损失系数。
根据以上理论,本文在对天津干线沿线实测水位数据进行计算和分析的基础上,复核有压箱涵的过流能力并对超设计能力供水的可能性进行研究。研究思路如下:
(1)通过实测典型流量下的沿线水面线数据,研究输水箱涵当前的实际糙率。
(2)如果实际糙率小于设计糙率,则按实际糙率和各保水堰的过流能力推算输水压力水头线,计算整个输水箱涵的最大过流能力。
(3)如果实际糙率大于等于设计糙率,则不能进行超设计能力输水,并给出按本工程内水压力设计标准下当前供水能力的下降值。
3 有压箱涵的糙率研究
如图1所示,天津干线有压输水箱涵存在保水堰的阻隔,由于保水堰流态复杂,且保水堰过流的水头损失以局部损失为主,糙率的变化主要对输水的沿程水头损失产生影响,因此,为避开保水堰的干扰,选择两保水堰间的箱涵段为研究对象。按照保水堰分布,把天津干线箱涵分割成8个区段,在各分段的起止位置安装水位计,通过水位同步测量技术测得各段起止位置处的实时水位差,根据式(2)~(5)即可计算得各段内的箱涵糙率(各分段内的局部水头损失根据《水力计算手册》中的规定和类似工程经验,按其占该段内沿程水头损失的5%~10%考虑)。通过测量和计算后所得的糙率结果见表1。

表1 各计算区段的糙率n
取计算所得各区段糙率的最大值0.012 9为当前箱涵段的实际过水糙率,以此作为天津干线有压箱涵的糙率,才能保证用于供水能力或供水水头计算,其结果是合理且偏于安全的。天津干线有压箱涵输水段设计采用糙率为n0=0.013 5,其实际运行糙率小于设计糙率,故认为箱涵内表面实际状态比设计状态“光滑”,具有一定的“超设计过流”能力,有压箱涵段具有进一步提高其供水能力的可能性。
4 “超设计能力”供水研究
天津干线设计最大供水流量为60 m3/s,设计采用糙率为n0=0.013 5,在设计最大供水能力Q=60 m3/s时,沿线各处的设计压力水头线已知。对于某一供水工况,由实测糙率n可计算各保水堰段之间总水头损失,采用传统堰流的水力学公式(见式(6)),可计算过保水堰时的水位变化,两者结合即可推算出天津干线沿程各处的水面线。
传统水力学公式中实用堰堰流公式:
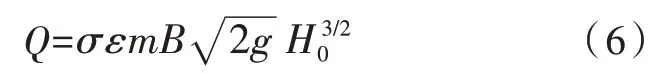
式中σ——过堰流的淹没系数,可由《水力计算手册》查得;
ε——过堰流的侧收缩系数,天津干线各堰无侧收缩,取ε=1;
M——过堰流的流量系数;
B——堰宽;
H0——堰上水头;
Q——过堰流量。
由此,采用当前选取的实际糙率n=0.012 9,结合式(6),在不改变设计安全超高设置原则的前提下,计算当沿线压力水头线与已知的设计最大供水能力Q=60 m3/s时的压力水头线重合一致时的实际供水流量,即可得到天津干线有压箱涵的超设计过流能力。
已知供水流量为60 m3/s时,4#保水堰上游侧的设计水位为18.038 m,若以此高程为起算点,往上游推算,水位推算结果见表2。

表2 水位推算结果表(3#堰下游达到设计水位时) m
由表2可知,天津干线输水流量仅提高至62.79 m³/s,十分有限。且上述计算是从天津干线整个有压箱涵段中间部位为比较的起点进行计算,如果把比较计算的起点后移到有压箱涵的末端,根据以上计算可知整个箱涵的“超过流”能力将随保水堰数量增加进一步降低。
综上所述,经对水位实测后,计算所得的箱涵实际糙率要小于设计糙率值,且个别区段还远小于设计糙率值,这意味着箱涵的过流能力具有较大的增加余地。但表2中的结果表明,从上游调节池到4#堰(雄安新区附近)段可增加的供水量非常小,这是由于在实测糙率小于设计糙率的前提下,箱涵段的过流能力会有所增加,但根据式(6),保水堰的过流能力仅与保水堰的布置形式和水头有关,过堰处的沿程水头损失在过堰总水头损失中占比很小,因此与沿程水头损失紧密相关的糙率对保水堰过流能力的影响也非常小。保水堰这种不受糙率影响的过流能力限制了天津干线整个有压箱涵系统输水能力的提高,故从当前技术来看,天津干线过流能力提高的余地非常小,对满足雄安新区和下游受水区的用水需求不具有实际意义。
5 结 语
本文通过对天津干线沿线各区段实测水位数据进行分析计算可知,箱涵段实际糙率比设计糙率取值小,故认为箱涵内表面较“光滑”,其具有一定的“超过流”能力;而保水堰主要水力要素为以局部损失为主的过堰流,过流面的光滑度对其过流能力影响不大,相较于设计值,保水堰不具有“超过流”能力,这限制了整个箱涵过流能力的提高。
