锦屏隧洞深部大理岩动力扰动力学特性试验研究
2021-09-26李邵军徐怀胜晏飞黄翔周济芳
李邵军,徐怀胜,2,晏飞,黄翔,2,周济芳
(1.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室,湖北武汉,430071;2.中国科学院大学,北京,100049;3.雅砻江流域水电开发有限公司,四川成都,610051)
随着国家基础设施建设的大规模推进,资源、能源开采逐渐转向深部,深部地下工程不断增加,如深埋长大隧洞、高应力地下厂房和矿山采场等。而深部工程岩体往往赋存于高地应力、构造活动强烈的复杂地质环境下,并受到开挖(采)工程活动、地震等带来的强动力扰动影响[1],由此带来的岩爆、应力型塌方等灾害频发,常导致设备损毁和人员伤亡[2]。为此,深部岩体工程在静、动力作用下的稳定性已成为当前和未来岩土力学和工程研究的热点和发展趋势[3−6]。
在大型深部隧洞工程建设和地质活动带来的动力扰动过程中,岩体始终处于相对高应力状态,如锦屏水电站交通洞和引水隧洞群,反演分析和测试获得的最大主应力甚至高达70 MPa[7−8]。对于此类深部岩体工程稳定性和支护设计问题的研究,仅考虑静态荷载作用或动态荷载的扰动,都不能完全与实际工程的工况相匹配[9]。
岩石的动静组合加载问题作为一个较新的研究方向,在2002年被首次提出[9],通常认为,工程活动中的扰动采用动静组合加载来模拟,比单纯采用静载作用或者只考虑动载作用更与实际工况相匹配,更有实际意义[10]。此后,国内外大量学者开展了此类研究,关于动静组合加载下的岩石力学特性,李夕兵等[11−13]开展了理论、实验和现场动力响应测试研究,获得了大量的有益成果。宫凤强等[14−17]将一维的动静组合荷载试验研究发展到二维,继而进一步扩展到三维试验研究。在此基础上,殷志强等[18−19]对岩爆及其岩石破坏过程进行了能量演化分析。
然而,对于深部岩石工程而言,不同岩体、不同应力条件下的隧洞动力响应、灾害特征和机理也不一样,目前对于考虑不同静态荷载情况且进行动态冲击断裂的试验与机理研究较为缺乏。为此,本文作者基于锦屏地下实验室隧洞工程,研究大理岩在不同静载情况下,加以冲击荷载作用时的动力学特性,并探究静载对大理岩冲击破坏的影响,揭示深埋隧洞工程动力扰动下的岩石力学参数变化规律和破坏响应特性,为深部地下工程建设与长期运行安全分析及支护设计提供支撑。
1 试样及实验系统
1.1 岩石试样
试验岩样取自锦屏地下实验室F支洞,埋深约2 400 m,该隧洞宽7.5 m,高8.0 m,为城门型截面。岩石取样位置如图1(a)所示。隧洞开挖过程中等岩爆频繁发生[20],现场施工开挖后的隧洞照片如图1(b)所示。

图1 锦屏地下实验室隧洞大理岩取样区Fig.1 Marble sampling zone in Jinping underground laboratory
试样为灰白色、灰黑色厚层块状白山组大理岩T2b。经矿物颗粒分析测试,其主要成分有白云石、方解石和云母,其质量分数分别为91.0%,8.6%和0.4%。
为满足霍普金森压杆(SHPB)系统试验要求,试样加工为直径50 mm,高25 mm 的圆柱体,按照岩石力学实验规范,对2 个端面进行磨平处理,并且其不垂直度和不平行度均严格满足实验要求。制样完成后,在岩样中心位置粘贴应变片,最终制得的大理岩岩石试样如图2所示。

图2 锦屏T2b大理岩试样Fig.2 Specimen of Jinping marble T2b
对该大理岩进行常规静态力学试验,获得其静态力学参数如表1所示。

表1 锦屏T2b大理岩静态力学参数Table 1 Static mechanical parameters of Jinping marble T2b
1.2 试验系统
本试验在国防科技大学霍普金森压杆(SHPB)装置上进行,SHPB 系统示意图[21−22]如图3所示,与无预加静载不同的是,本试验在吸收杆后方设置一个千斤顶,实现预加荷载PS的施加与保持,该装置冲击断裂试验应变率范围为101~103s−1。动拉伸和动压缩试验中,冲击加载为恒应变率的半正弦波应力脉冲,加载模型如图4所示。数据采集系统除了常规采集输入杆和输出杆应变外,在动拉伸试验时特别对岩石中心点位置应变进行全过程动态监测。

图3 霍普金森杆系统示意图Fig.3 Schematic diagram of SHPB system
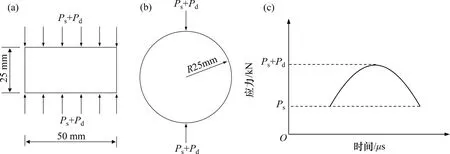
图4 动静组合试验加载模型Fig.4 Loading model of static-dynamic coupling loading test
2 试验结果及分析
2.1 岩样拉伸断裂和压缩断裂破坏情况
图5所示为动静组合压缩情况下大理岩的主要断裂破坏形态。从图5可知:动静组合加载岩样的破坏形态均为劈裂破坏,随着应变率的增大,劈裂破坏加重,最终成粉状。

图5 动静组合压缩岩样破坏情况Fig.5 Damage under dynamic-static coupling compressive loading
图6所示为动静组合拉伸情况下的岩石破坏形态。从图6可以看出:按照巴西劈裂原理,该试验很好地吻合其破坏形态,沿着加载轴形成了巴西劈裂破坏形态。劈裂破坏形成2 个较为完整的块体,并且在较短时间内,在实验杆之间尚有一定的承受荷载的能力,因此表现出应变最大发生破坏时应力并没有达到最大的试验偏差问题。

图6 动静组合拉伸岩样破坏情况Fig.6 Damage under dynamic-static coupling tensile loading
2.2 大理岩动静组合加载试验的应力应变分析
与常规SHPB实验不同的是,为了准确跟踪岩样中心位置处的应变情况,特别在测试岩样的中心位置安置应变片,以监测岩样断裂破坏的应变演化全过程。岩样断裂破坏过程中应力应变关于时间的变化曲线如图7所示。
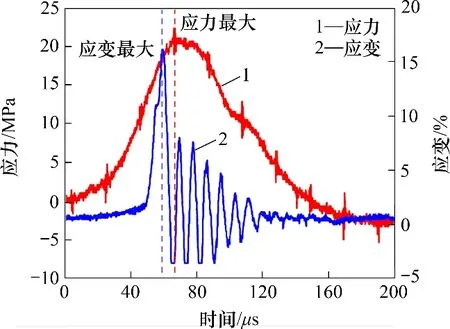
图7 加载过程应力和应变时间曲线Fig.7 Stress and strain curves of loading process
由图7可见:在加载过程中,应力与应变到达峰值并不同步,当应变达到最大即试样破坏时,应力峰值有明显的滞后现象。原因在于,在加载过程中,应变到达峰值后,岩样断裂成2部分,但这2 块断裂岩样仍相互嵌合夹在2 个加载杆之间,仍能承受较大荷载,因此,在应力上表现为峰值滞后,测试获得的应力偏大。基于此,所有试验结果基于应变监测进行修正,避免出现偏大的现象。
动拉伸应力时程曲线(静载0 MPa)及动压缩应力−应变曲线(静载10 MPa)如图8所示。由图8可见:在动拉伸条件下,静载为0 MPa时,随着加载速率降低,峰值强度从876 GPa/s下降到207 GPa/s,在动压缩条件下,静载为10 MPa 时,随着加载速率降低,峰值强度从581 GPa/s 下降到391 GPa/s。由此可知,随着加载速率的降低,试样的破坏强度显著降低,但加载速率下降到一定程度之后,试样破坏所需的时间及相应应变率也会增加。

图8 典型加载过程应力时程曲线及应力−应变曲线Fig.8 Typical stress curves of loading process and stressstrain curves
2.3 大理岩动静组合压缩实验结果
不同静载情况下的大理岩动态压缩强度实验结果如图9所示。从图9可知:大理岩动压缩强度与加载速率之间具有很强的线性相关性,且在低加载速率时,大理岩动态压缩强度对静态载荷敏感性较低,在140~160 MPa之间;随着加载速率的增大,动压缩强度线性增大且静载影响突显,其中在静载为10 MPa 时,试样动压缩强度增幅最大,20 MPa时次之,无静载时最小。可知,对大理岩进行动静组合压缩试验时,在静载为0~20 MPa时,随着静载的增大,试样动压缩强度先增大后减小,且增幅大于减幅。

图9 动静组合压缩实验结果Fig.9 Experimental results under dynamic-static coupling compressive loading
不同静载情况下的动静组合压缩情况下的动态弹模的结果如图10所示。由图10可知:大理岩动压缩强度与加载速率之间同样具有很强的线性相关性,但与动压缩强度不同的是,不同静载下的动弹性模量随加载速率的变化趋势相近,但静载为10 MPa 时,试样动弹性模量最大,无静载时次之,静载为20 MPa 时,最小。这是因为:静载较小时,岩体被压密,从而导致其动压缩强度和动弹模都相应增大;而静载较大时,岩体产生一定的损伤,导致其弹模和强度又开始下降。

图10 动静组合压缩下动态弹性模量Fig.10 Dynamic elastic modulus under dynamic-static coupling compressive loading
2.4 大理岩动静组合拉伸实验结果
根据表1,大理岩静载抗拉强度为4.5 MPa,因此,选择接近该抗拉强度50%的2 MPa 作为最高静载。在动态拉伸试验中,分别取静载为0,1.0和2.0 MPa,得到不同静载下大理岩动拉伸强度,并对结果进行线性拟合,如图11所示。从图11可以看出:大理岩动拉伸强度与加载速率之间线性关系明显,且在不同静载下,其线性变化趋势相同;动拉伸强度与加载速率呈正相关,与静载呈负相关,且静载每增大1 MPa,动拉伸强度减小约2 MPa。

图11 动静组合加载下动拉伸强度Fig.11 Dynamic tensile strength under dynamic-static coupling tensile loading
2.5 大理岩动拉伸强度影响因素与分析模型
在动静组合加载情况下,大理岩动拉伸强度与预加静载、加载速率有关,除此之外,大理岩静态拉伸强度也会影响大理岩动拉伸强度。基于此,考虑以上3个因素,建立大理岩动拉伸强度拟合分析模型如下:

式中:σ0为静态抗拉强度;σs为预加静载;为加载速率;为参考加载速率;A,B,n为拟合系数。拟合可得:

从式(2)可知:大理岩动静组合荷载下动态拉伸强度与静态拉伸强度为线性关系,与预加静载和加载速率为非线性关系,其拟合曲线如图12所示。从图12可知:在低加载速率下,随着加载速率的增大,大理岩动态拉伸强度出现一个快速增大阶段,此阶段,动拉伸强度受静载影响较小;随着加载速率的增大,大理岩动拉伸强度增速放缓,此阶段,预加静载影响突显。整体上大理岩动拉伸强度与预加静载之间呈现负相关线性关系,与加载速率之间呈现正相关指数关系,与静态拉伸强度之间为正相关线性关系。
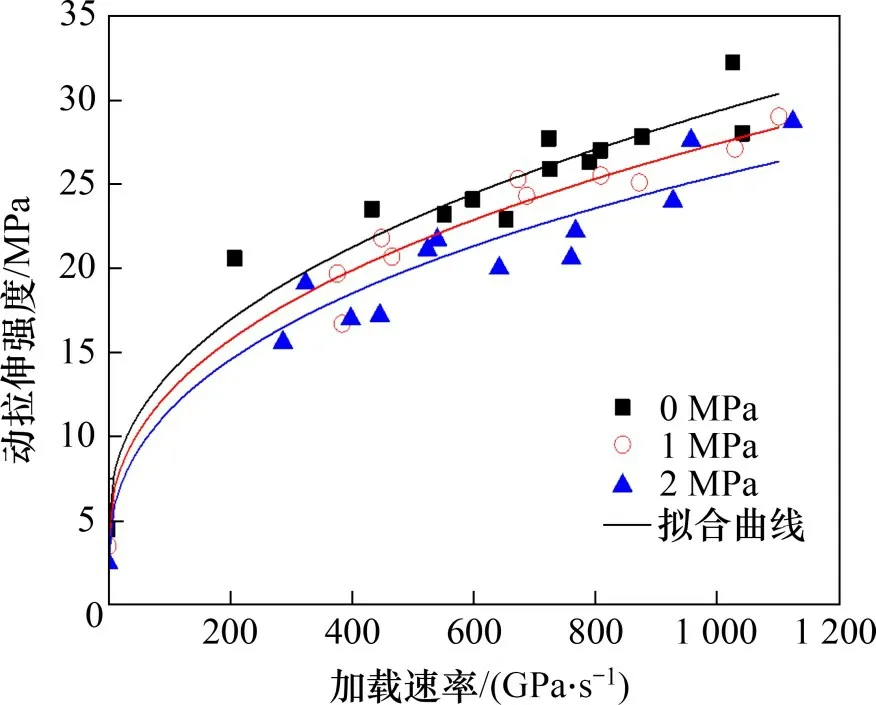
图12 动静组合动拉伸强度拟合曲线Fig.12 Fitting curves of dynamic tensile strength under dynamic-static coupling tensile loading
3 结论
1)无论是动压缩还是动拉伸,其强度受动态荷载的加载速率影响较大,并且随着冲击荷载加载速率的增大,强度相应明显增大。
2)对于动压缩来说,随着静态荷载的增大,动压缩强度先增大后出现减小,在静载10 MPa下,动压缩强度最大,静载20 MPa 时,动压缩强度次之,无静载时,动压缩强度最小。加载速率越大,动压缩强度受静载影响越大,加载速率较小时,动压缩强度受静载影响较小。岩样的压缩破坏形态在低加载速率下产生劈裂裂纹而破坏,高加载速率下劈裂成粉状而破坏。
3)对动拉伸破坏实验过程进行全过程动态应变监测表明,大理岩冲击断裂破坏过程中,岩石应力和应变达到峰值时并不同步,以试验最大应力作为岩石动拉伸强度的实验方法得到的实验结果偏大,因此,建议冲击拉伸实验动拉伸强度以应变监测进行修正。
4)对于动静荷载拉伸实验,随着静载载荷的增大,动拉伸强度明显减小,并且静载每增大1 MPa,动拉伸强度减小约2 MPa。大理岩动态拉伸强度与静态拉伸强度和预加静载呈线性关系,与加载速率成指数函数关系。
