特高压直流接地极入地电流对高速铁路综合接地系统腐蚀影响研究
2021-09-26陈汉杰张华志
陈汉杰,张华志,黄 军,宋 伟,张 波
(1.中铁第四勘察设计院集团有限公司,武汉 430063; 2.电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系),北京 100084)
实际工程中,受线路走向、土地规划等因素制约,不可避免地会出现高速铁路和特高压直流工程接地极邻近的情况,如合福高铁、昌景黄铁路项目等。高速铁路综合接地系统具有距离长、多点接地的特性,存在直流通道,但目前特高压直流工程在选址时,仅遵循原则上直流接地极距离变电站、发电厂、管道和非电气化铁路等地下金属构件不小于10 km[1],并未对邻近情况下的特高压直流工程对高速铁路的影响进行定量评估研究。
目前,特高压直流接地极对邻近地下金属设施腐蚀的问题,主要研究集中在油气管线腐蚀[2-3],天然气管线腐蚀[4-5],电力系统输电线路杆塔接地体腐蚀[6-7],而鲜见对高速铁路综合接地腐蚀的研究。特高压直流工程对铁路的影响研究,则主要集中在牵引供电系统直流偏磁方面,在仿真计算建模时并未考虑接触网支柱,路基、桥梁、隧道结构钢筋等散流通道。刘士利等[8-10]以非高速铁路为研究对象,建模时接地散流通道仅考虑钢轨与贯通地线。青攀[11]以高速铁路为研究对象,但在建模时同样只考虑牵引网的参数,并未考虑综合接地系统。
实际上,高速铁路综合接地系统[12-14]直流通路除钢轨、保护线、贯通地线外,路基、桥梁、隧道、接触网支柱等结构也存在直流通路,导致以上结构也会受到直流电流影响。因此,有必要研究考虑结构钢筋的高速铁路综合接地系统的直流参数,再基于此研究特高压直流输电对邻近高速铁路地下金属设施腐蚀的问题。
1 典型高铁工程段直流通路参数
1.1 各工程段直流电阻与接地电阻的计算方法
首先在CDEGS软件中基于实际工程参数与空间布置方案建立仿真模型,如图1所示。模型建立完毕后,如图2所示,电磁场软件中该模型一侧端部注入单位电流Ia,另一侧抽出该电流Ia,通过电磁场仿真软件计算得出此局部模型上的电压和电流分布,然后将中间一定长度设为L,两点之间的电位差即Ua-Ub和该段中间位置流过的电流I相除,从而可求得长度L下沿线路方向的总直流电阻值。

图1 典型工程区段局部仿真模型

图2 直流电阻/直流接地电阻计算示意
由于高铁线路直流电阻值较低,可认为其为均匀散流模型,在电磁场软件中从该模型一侧注入电流,再次通过电磁场仿真软件计算得出此局部模型上的电压和电流分布,求取模型中点处平均电位值U和L长度模型的总泄漏电流值Iz,二者相除可得出此L长度下垂直入地方向接地电阻值。
获得沿线路方向的总直流电阻值和垂直入地方向的接地电阻值后,基于传输线等效模型的构建思想,可利用“Π”形等效电路来分析直流接地和入地电流对高铁系统的影响。
由于目前没有公开的直流输电地中回流在高速铁路系统分布的测试数据,所建立的模型无法通过实测验证,但建模原理与直流输电地中回流在交流电网、油气管道的模型原理相同,相应参数计算方法也相同[15-17],可间接保证模型的有效性。
1.2 路基段直流通路参数
高速铁路路基段工程综合接地系统是由保护线、钢轨、贯通地线、道床板接地钢筋和接触网支柱等设施共同构成的立体接地网络。根据设施所在的空间位置,可将整个接地系统分为位于水硬结合层上的地上部分(包括保护线、钢轨、道床板接地钢筋)和埋设于土壤中的地下部分(包括贯通地线和接触网支柱基础),如图3所示。考虑到道床板结构中仅浇筑承载层及以上部分,其包含钢筋结构、水硬结合层,常采用电气绝缘素水泥,因此,道床板中接地钢筋无法向大地散流,仅能和保护线、钢轨等地上部分相互分流。为保证道床板中接地钢筋不向大地散流,选择在仿真模型中两侧贯通地线上方(地上1 m处)设置道床板接地钢筋,规格为φ20 mm。路基段沿线接触网支柱的基础钢筋和贯通地线连接后也可作为接地极。接触网支柱结构内部为金属钢管,外部为水泥支撑,埋设在土壤中和大地直接接触散流。可将接触网支柱等效为内部空心钢管,外部包裹一定厚度涂层的导体。
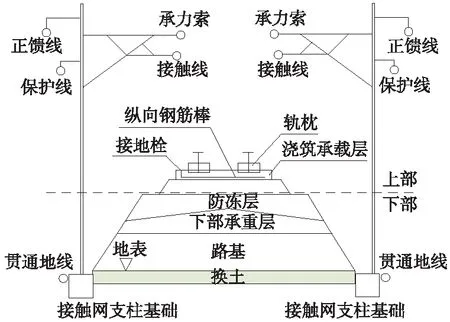
图3 典型路基区段断面示意
仿真模型中取钢管半径0.4 m,内径0.39 m,混凝土涂层厚0.05 m。每50 m在两根贯通地线上各设置1段垂直入地3 m的导体(等效为接地网支柱)。同时,路基段的上下行保护线和上下行钢轨、贯通地线会在扼流变处互联。基于以上信息,在CDEGS中建立仿真模型,选取不同长度的路基段模型求取直流电阻和接地电阻,土壤电阻率取30 Ω·m,包覆层电阻率取100 Ω·m,结果见表1。

表1 不同长度路基段模型计算结果
从表1可以看出,不同长度模型计算得出的路基段直流接地电阻和直流电阻相差很小,不同的建模长度不会对计算单位长度电阻值的结果产生影响。为方便利用单元模型搭建长距离高铁线路接地系统模型,后续计算都选取1.5 km为1个“Π”形电路单元,计算直流接地电阻和直流电阻值。
1.3 桥梁段直流通路参数
高铁桥梁一般由上部结构、下部结构、支座和附属构造物组成。其中,上部结构又称桥跨结构,是跨越障碍的主要结构;下部结构包括桥墩、桥台和基桩。桥梁的综合接地系统是由保护线、钢轨、贯通地线、桥梁结构物中的非预应力结构钢筋(接地钢筋)等设施共同构成的立体接地网络,如图4所示。
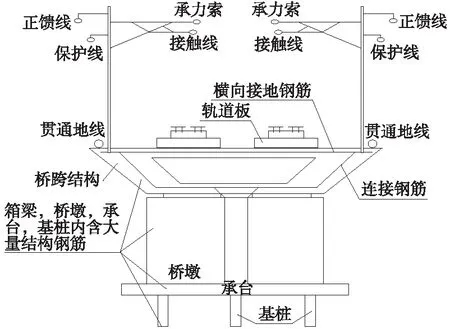
图4 典型桥梁区段断面示意
桥梁梁体内部存在大量接地钢筋且彼此横纵相连,在接地系统中起到了分流作用。铁路系统中的桥梁具有多种类型[18],选取最典型的简支箱梁结构作为建模对象[19],在CDEGS中建立仿真模型,包覆层电阻率取100 Ω·m,1.5 km桥梁段的仿真计算结果如表2所示。

表2 不同土壤电阻率桥梁段模型计算结果
由表1、表2可见,桥梁段的直流电阻值小于路基段的直流电阻值,这主要是由于桥梁梁体内部存在大量钢筋,起到了减小直流电阻的作用。
1.4 隧道段直流通路参数
高铁隧道根据地质条件不同,将隧道所穿围岩分为Ⅰ~Ⅵ级。分别选取Ⅱ级和Ⅴ级2种典型围岩为例,进行隧道接地系统建模[20-21]。
Ⅱ级围岩隧道综合接地系统如图5所示,其是由保护线、钢轨、贯通地线、底板接地钢筋、连接钢筋等设施共同构成的立体接地系统网络。隧道底板接地钢筋按每间隔1个台车位设置1处,由大小为10 m×4 m的1 m×1 m双层网格构成,采用φ10 mm钢筋。隧道底板钢筋包裹水泥找平层在CDEGS软件中可等效为底板接地钢筋外部包裹厚30 cm涂层的导体。

图5 Ⅱ级围岩隧道区段断面示意
在CDEGS中建立仿真模型,包覆层电阻率取100 Ω·m,1.5 km的Ⅱ级围岩隧道仿真结果如表3所示。可以看出,Ⅱ级围岩隧道段的直流电阻值与路基段基本一致,直流接地电阻值小于路基段的接地电阻值,主要因为Ⅱ级围岩隧道中的底板接地钢筋较多,起到了较好的散流作用。
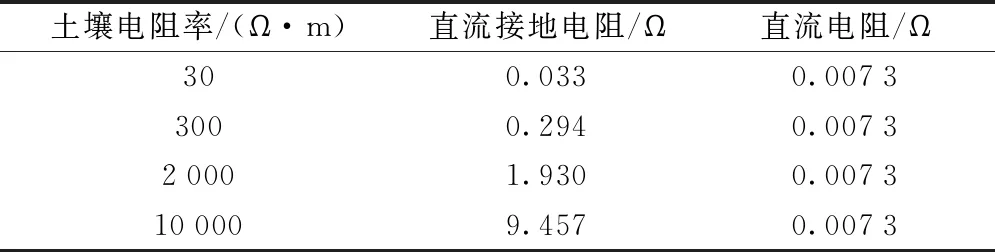
表3 不同土壤电阻率下Ⅱ级围岩隧道段模型计算结果
Ⅴ级围岩隧道综合接地系统如图6所示,其是由保护线、钢轨、贯通地线、纵向接地钢筋、环向结构钢筋和锚杆等设施共同构成的立体接地系统网络。隧道内纵向接地钢筋选取φ16 mm钢筋,该钢筋每100 m断开一次,纵向接地钢筋和贯通地线每100 m互联一次。隧道锚杆通过环向结构钢筋与纵向接地钢筋连接,锚杆接地体以1个台车长度为间隔设置。锚杆和纵向接地钢筋均采用φ16 mm钢筋,锚杆长4 m,间距1.5 m,环形钢架采用HW150型钢。基于以上参数,选取1.5 km的Ⅴ级围岩隧道段作为一个模型单元进行建模,包覆层电阻率取100 Ω·m,仿真结果如表4所示。可以看出,Ⅴ级围岩隧道段的直流电阻值与路基段基本一致,直流接地电阻值小于路基段和Ⅱ级围岩隧道段的接地电阻值,这是由于Ⅴ级围岩隧道中的隧道锚杆与环形钢架起到了较好的散流作用,降低了接地电阻。
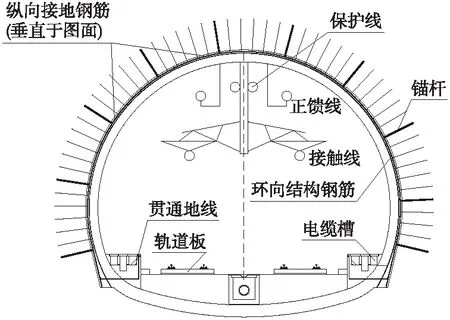
图6 V级围岩隧道区段断面示意

表4 不同土壤电阻率V级围岩隧道段模型计算结果
2 不同高铁工程段电化学腐蚀影响仿真计算
直流接地极入地电流对金属物的腐蚀程度取决于导体同周围介质的交换电流密度,电流密度越大,参与反应的金属离子越多,金属的电解速度就越快。以高铁线路接地系统单位长度的泄漏电流密度指标,来衡量高铁线路各位置处受到电化学影响的腐蚀程度。
取土壤电阻率300 Ω·m,接地极中心到长度204 km的高铁线路垂直距离为5 km,包覆层(水泥)电阻率为100 Ω·m,直流接地极选择典型参数,外环φ800 m,内环φ500 m,截面φ70 mm,埋深3 m,入地电流3 000 A。不同204 km工程段(全路基、桥梁、隧道)下得到的高铁线路接地系统沿线单位长度泄漏电流密度如图7所示,最大值如表5所示。可以看出,桥梁段的泄漏电流密度最大,这是由于桥梁路段直流电阻远低于其他路段,聚流效应更明显。
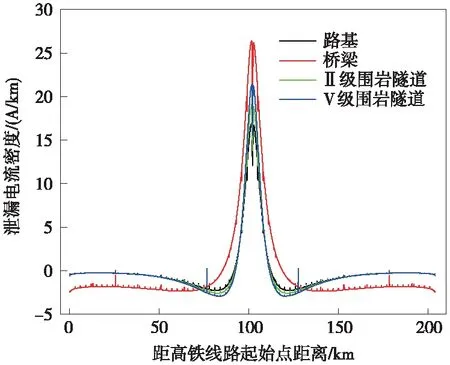
图7 不同工程段高铁线路接地系统沿线泄漏电流密度

表5 不同高铁路段下泄漏电流密度最大值 A/km
3 直流接地极对高铁综合接地腐蚀的影响规律
以路基段为例,分别以接地极工作方式、土壤电阻率及接地极-线路垂直距离为变量,研究直流接地极对高铁综合接地腐蚀的影响规律。
3.1 接地极工作方式的影响
接地极具有阳极工作与阴极工作方式,以路基工程段为例,两种方式下高铁线路接地系统沿线单位长度泄漏电流密度仿真结果如图8所示。

图8 不同方式工作时系统沿线单位长度泄漏电流密度
由图8可以看出,当接地极为阳极工作时,由于靠近直流接地极的高铁线路中间路段部分泄漏电流方向是流入高铁线路,而流入的直流电流会在高铁线路接地系统分流,随着远离直流接地极,泄漏电流方向是流出高铁线路,此时靠近中间路段两侧的波峰位置为腐蚀风险增强区域,该风险区域泄漏电流密度最大值为2.26 A/km。当接地极为阴极工作时,由于靠近直流接地极的高铁线路中间路段部分泄漏电流方向是流出高铁线路,此时中间路段的位置为腐蚀风险增强区域,该风险区域泄漏电流密度最大值为16.89 A/km。所以,当接地极为阴极工作时,距离其最近的高铁线路段受到的电化学腐蚀影响最大。
3.2 土壤电阻率的影响
分别取土壤电阻率30,300,2 000 Ω·m进行计算,结果如图9所示。当土壤电阻率逐渐增大时,沿线泄漏电流密度最大值分别为7.54,16.89,23.35 A/km。由图9可以看出,当土壤电阻率较低时,由于接地极入地直流电流散流较好,高铁接地系统受到的电化学腐蚀影响最小;反之,在高土壤电阻率时,高铁接地系统聚流效应明显,高铁线路中间段泄漏电流密度较高,加大了直流接地极入地电流对高铁接地系统腐蚀的影响。
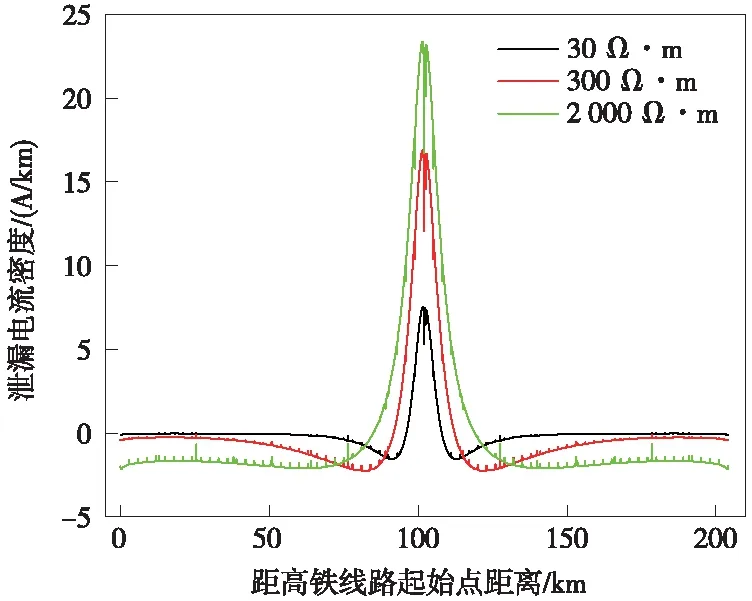
图9 不同土壤电阻率下系统沿线泄漏电流密度
3.3 接地极—高铁垂直距离的影响
取接地极中心到高铁线路的垂直距离分别为5,10,20 km,土壤电阻率为300 Ω·m,计算结果如图10所示。当垂直距离逐渐增大时,沿线泄漏电流密度最大值分别为16.89,5.36,1.41 A/km。由图10可以看出,当土壤电阻率固定时,高铁线路距接地极距离越近,高铁线路接地系统中间腐蚀风险增强区域的沿线泄漏电流密度越大,中间路段受到电化学腐蚀的影响越严重。
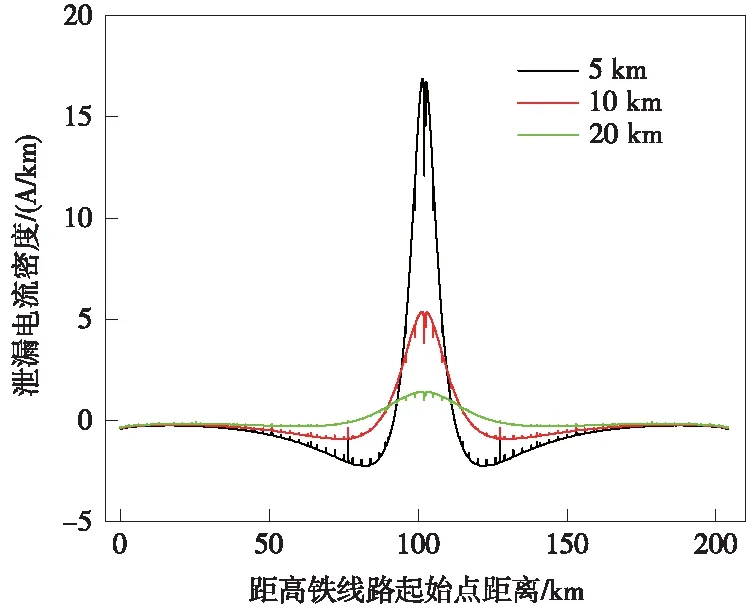
图10 不同垂直距离下系统沿线泄漏电流密度
4 结论
针对特高压直流接地极以大地为回路运行时对高速铁路综合接地系统腐蚀的问题,对不同的高速铁路工程段综合接地系统进行直流参数仿真计算,并基于此评价各工程段的电化学腐蚀风险,研究了影响高铁工程段综合接地系统电化学腐蚀的因素,得出如下结论。
(1)不同高铁工程段综合接地系统各不相同,但都可以归结为对模型直流电阻和直流接地电阻的求取,进而可采用“Π”形等效电路来分析直流接地极入地电流对高速铁路综合接地系统的影响。
(2)土壤电阻率、接地极与工程段的垂直距离、接地极的工作方式均影响高速铁路综合接地电化学腐蚀行为。当接地极阴极工作,接地极邻近线路为桥梁区段,土壤电阻率较高,或接地极—高速铁路间距较小时,高铁综合接地系统电化学腐蚀越严重。
研究结论可为今后高速铁路及特高压直流接地极的选址提供参考。
