自然风条件下寒区高速铁路隧道温度分布及防冻保温长度研究

赵希望,马勤国,姜海强,蓝天立

(1.广东省隧道结构智能监控与维护企业重点实验室,广州 511440； 2.中铁隧道局集团有限公司勘察设计研究院,广州 511440； 3.华南理工大学土木与交通学院,广州 510641)

引言

随着“一带一路”倡议的持续推进和进一步实施，我国东北和西北高纬度、高海拔严寒地区隧道工程及其他交通设施的修建不断增加。例如，哈大高铁九里庄隧道、京沈高铁梨花顶隧道、吐库二线中天山隧道、敦格铁路当金山隧道、兰新二线祁连山隧道等。与其他地区的隧道不同，在高纬度、高海拔严寒地区修建隧道常常会出现严重的冻害现象，如拱顶吊冰柱、边墙冻胀开裂、排水管冻结堵塞等[1-3]。这些冻害问题很大程度上弱化了隧道的使用功能，给铁路的正常运营带来极大的安全隐患。迄今为止，由于冻害问题，我国西北和东北地区的很多严寒地区隧道常年有8～9个月不能使用，甚至有些隧道在冻胀力作用下衬砌裂缝达5 cm，渗漏水问题相当严重[4]。因此，开展严寒地区隧道防冻保温措施的研究显得异常迫切。

严寒地区隧道出现冻害的根本原因是围岩或围岩-衬砌之间积聚的水分在负温环境下发生冻结。严寒地区隧道修筑后，打破了围岩的原始热平衡，寒季围岩因其中的水分冻结成冰而体积增大，对衬砌产生冻胀力，使衬砌和围岩发生相对位移；在暖季，围岩中冻结的冰融化成水，冻结时产生的位移因不能完全恢复而在围岩及衬砌-围岩之间留下空隙，这些空隙会增加围岩中水分的聚集，使来年的冻胀更加严重。这种衬砌背后围岩的冻融反复作用会使衬砌防水层发生破损，甚至衬砌开裂。因此，分析隧道围岩温度的分布规律对研究严寒地区隧道冻胀产生机制和解决隧道冻害问题具有重要意义。

近年来，学者们对严寒地区隧道围岩温度场分布规律进行了大量研究并取得了一定成果。在理论方面，冯强等[5]采用Laplace积分变换的方法求解传热模型，得到寒区隧道温度场的解析分析方法。在室内试验方面，黄继辉等[6]得到了寒区公路隧道冻胀力的分布形式和计算方法。在现场监测方面，郑波等[7]对隧道冬季洞口段衬砌开裂、春融期渗漏水的发生机理进行了研究，并提出了整治措施；陈建勋[8]通过对严寒地区隧道进行现场测试，揭示了隧道温度场的变化规律；罗彦斌[9]以典型隧道现场实测数据为基础，以围岩温度场分布为依据，对寒区隧道冻害等级进行了划分。在数值计算方面，李彬嘉等[10]建立了寒区隧道有限元模型，研究寒区隧道在内部气温变化作用下的冰-水相变发展过程；高焱等[11]采用数值分析研究不同列车运行速度和运行间隔工况下，寒区隧道温度场的分布规律；LI等[12]和MA等[13]建立了考虑冻结过程中水分相变和水分迁移的水-热耦合传热方程，对寒区隧道温度场分布规律进行了研究，并提出了保温层参数(厚度和导热系数)的确定方法。以上研究均在隧道衬砌壁面温度确定的情况下进行。但是当隧道贯通之后，由于隧道进口和出口存在压力差，寒区隧道洞外的空气在压力差的作用下会进入隧道，进而改变隧道壁面的温度。特别在寒季，隧道围岩温度因山体内部热能的影响相对外界环境温度要高很多，于是进入隧道内的冷空气和围岩衬砌壁面会发生强烈的热交换，从而改变围岩的温度场。因此，要想准确分析隧道内围岩和衬砌的温度分布规律和确定恰当的防冻保温措施，就需要对自然风条件下隧道围岩-衬砌温度分布规律进行深入研究。而目前考虑自然风情况下，空气与隧道衬砌壁面热交换和衬砌-围岩热传导的研究相对较少。

鉴于此，根据传热学、流体动力学、冻土学的基本原理和方法，以吉图珲高速铁路榆树川隧道为依托，建立自然风条件下考虑围岩冰-水相变的寒区隧道空气与衬砌热交换和衬砌-围岩热传导的热流固耦合模型。运用该模型对榆树川隧道在自然风条件下空气与隧道衬砌热交换和围岩热传导耦合问题进行研究，分析隧道围岩温度的分布规律，并探讨了隧道冻结长度与风速的关系。

1 工程概况

1.1 隧道概况

榆树川隧道位于延吉市安图县境内，是新建吉图珲高速铁路的控制性工程，隧道洞口如图1所示。隧道全长2 210 m，最大埋深约160 m，全隧位于直线段上，内纵坡设计为单面坡，坡度5‰，隧道断面尺寸如图2所示。在榆树川隧道进口段安设气象站，对隧址2018年12月至2019年12月的气温、风向和风速进行了监测。根据监测数据，每年自10月中旬至次年4月中旬为冻结期，最低气温出现在1月份，全年最高气温和最低气温分别为37.62 ℃和-21.92 ℃。隧道进口处平均风速为2.08 m/s，最大风速为5.44 m/s，风向与隧道走向大体一致，即风从隧道进口吹入，从出口吹出。隧道进口处空气日平均温度如图3所示。

图1 榆树川隧道洞口

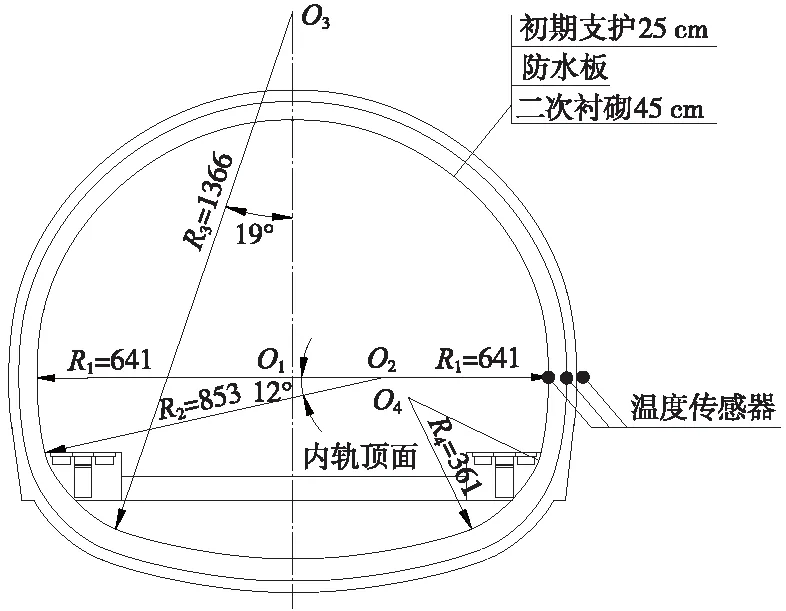
图2 榆树川隧道断面尺寸(单位：cm)

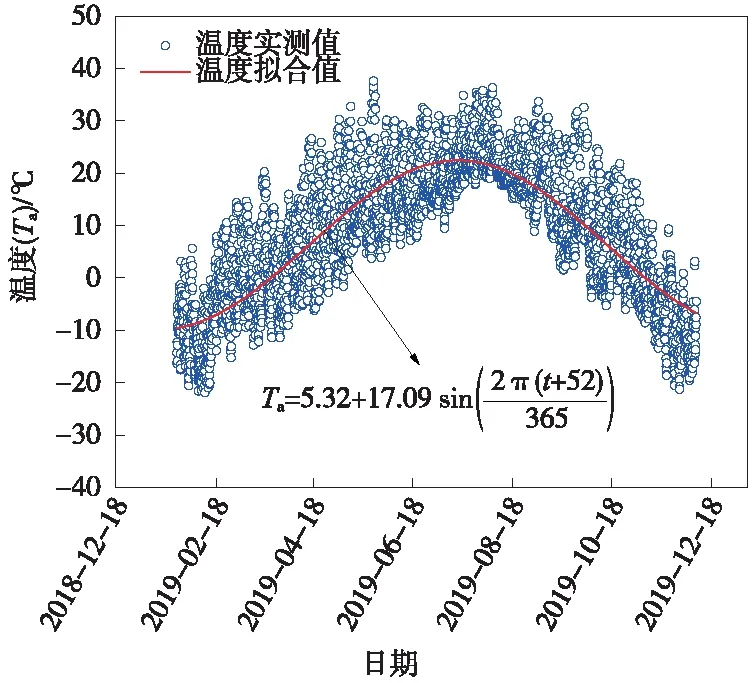
图3 隧道外大气温度

1.2 隧道冻害现状

吉图珲高速铁路已通车5年，榆树川隧道在运营过程中发生明显的冻害，具体表现为：2017年12月18日，隧道K352+601(距离隧道进口594 m)处，距起拱线以上高约3.5 m处出现施工缝半月形(直径约0.15 m)裂纹成线状滴水，顺施工缝以下边墙周围伴随有小部分结冰，见图4(a)。2018年1月9日，隧道K352+695(距离隧道进口696 m)和K352+699(距离隧道进口700 m)处，拱腰两侧(照明线上1.5 m高处)均挂冰数根，环向排列，长5～20 cm。2018年1月21日，隧道K352+912(距离隧道进口905 m)处正拱顶注浆孔挂冰，且成线状滴水，见图4(c)。

图4 榆树川隧道冻害

针对榆树川隧道出现的不同情况冻害，采取了不同的防冻措施，如针对边墙渗水冻结，采取“安设钢边止水带流水槽、边墙打孔泄压”引排渗水的方式，见图5(a)；针对拱腰两侧滴水挂冰，采用在边墙打泄水孔，铺设“PVC管+电伴热+镀锌铁管+玻璃丝棉卷毡”的措施，见图5(b)。

图5 榆树川隧道冻害防治措施

由现场隧道冻害发展情况和发生位置可以看出，隧道冻害的发展是逐步出现的，先出现在距离隧道进口较近处，后出现在距隧道进口远的位置，至2018年1月21日，隧道冻害已经扩展到距隧道进口900 m处。因此，隧道冻害的发展与冬季自然风作用密切相关，需对自然风条件下隧道围岩-衬砌温度分布规律进行分析，进而确定隧道的冻结长度。

1.3 隧道温度监测

为得到衬砌和围岩温度场分布规律、隧道纵向温度分布规律，在隧道中选取典型断面和典型位置进行温度监测，具体方案如下。

(1)洞内纵向温度场监测方案

从隧道进口开始，在隧道拱腰位置布设温度监测点，共布设11个点。具体位置为Z 1号(隧道进口处)、Z 2号(距进口50 m)、Z3号(距进口150 m)、Z4号(距进口350 m)、Z5号(距进口650 m)、Z6号(距进口1 103 m)、Z7号(距进口1 557 m)、Z8号(距进口1 857 m)、Z9号(距进口2 057 m)、Z10号(距进口2 157 m)、Z11号(隧道出口处)，见图6。

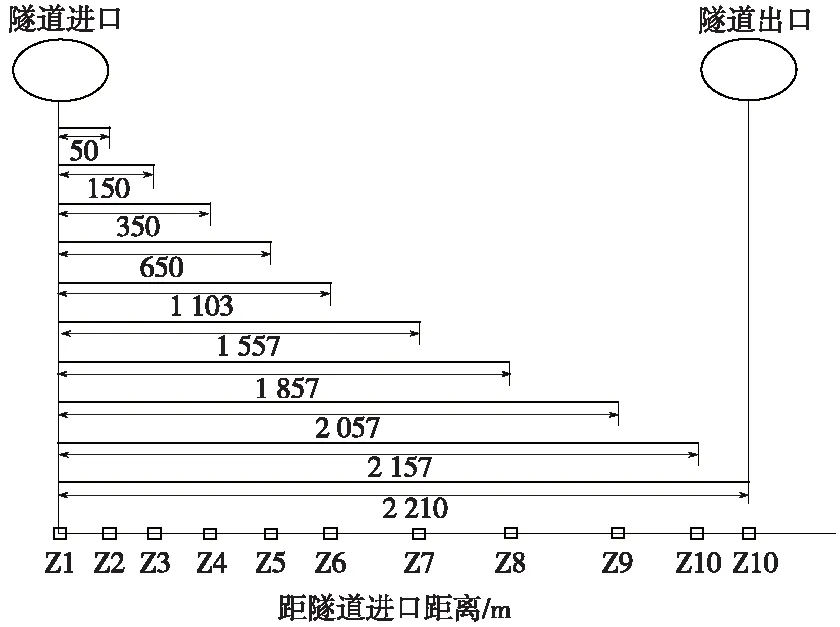
图6 隧道温度监测断面示意

(2)围岩及衬砌温度监测方案

从隧道进口到出口，在隧道拱腰位置共布设11个温度监测点，每个监测点布设3个温度传感器，见图2，分别在1号(二次衬砌表面)、2号(二次衬砌与防水板之间)、3号(初期支护外表面)。

图7为监测最冷月榆树川隧道不同进尺及深度处平均温度分布。由图7可以看出，隧道二次衬砌表面、二次衬砌与防水板之间和初期支护外表面的温度均呈“两头低，中间高”的分布规律。因隧道发生冻害的原因主要是水分发生冻结和膨胀，所以二次衬砌背后低于0 ℃的长度定义为冻结长度。由现场监测温度数据可知，榆树川隧道进口段冻结长度为1 443 m，出口段冻结长度为29 m。隧道进出口段冻结长度相差较大的原因是隧址处自然风风向与隧道走向大体一致，风从隧道进口吹入，从出口吹出，对进口有显著的影响。

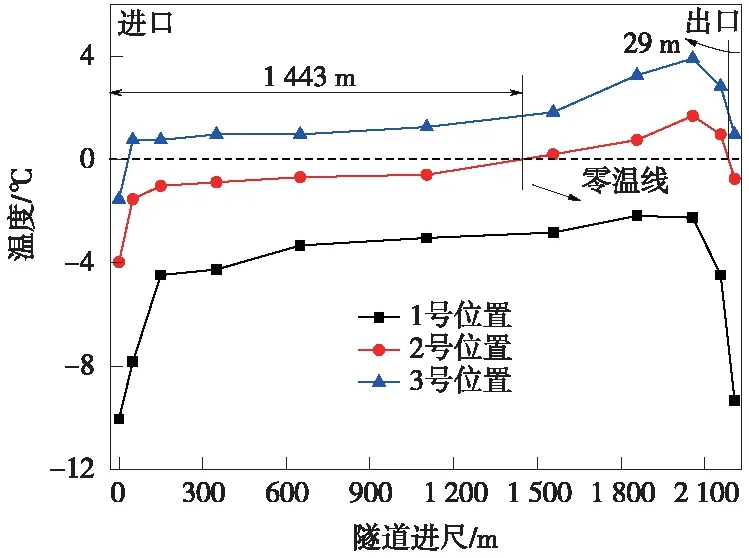
图7 最冷月隧道不同进尺、不同深度处平均温度

2 严寒地区隧道温度场计算模型

2.1 隧道内空气传热方程

根据前人的研究成果[14-16]，隧道内空气的流动和传热过程做出以下假设：(1)隧道内空气为不可压缩流体；(2)空气密度为常数；(3)空气温度的变化对空气的流动无影响；(4)空气在隧道内的流动为层流。隧道内空气层流热交换的控制方程如下[17]。

2.1.1 连续性方程

∇·(u)=0

(1)

式中，u为空气流动速度，m·s-1。

2.1.2 动量方程

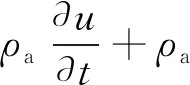
(2)

式中，p为空气有效压力，Pa；μ为空气动力黏度，Pa·s；ρa为空气密度，kg·m-3；t为时间，s。

2.1.3 能量方程

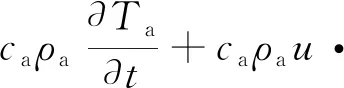
(3)

式中，Ta为空气温度，K；λa和ca分别为空气的导热系数和比热容，单位分别为W·m-1·K-1和J·kg-1·K-1。

2.2 隧道围岩传热方程

围岩在冻结时水蒸气蒸发耗热很少，同时水分迁移带动的热量迁移也很小[18]，故在计算中忽略了对流、质量迁移等其他作用，只考虑岩土体骨架和孔隙水的热传导及冰-水相变作用，隧道围岩传热控制方程如下[18-20]

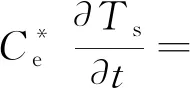
(4)

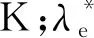
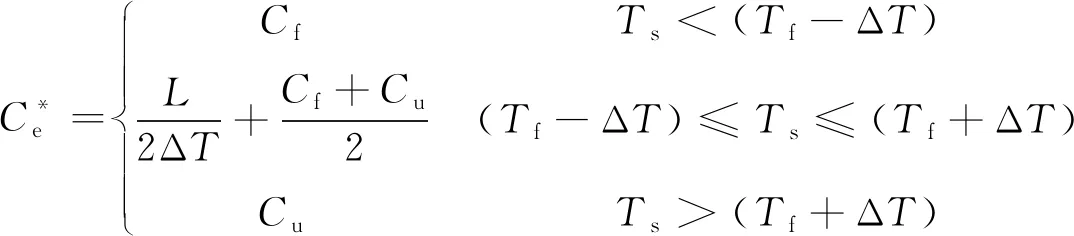
(5)

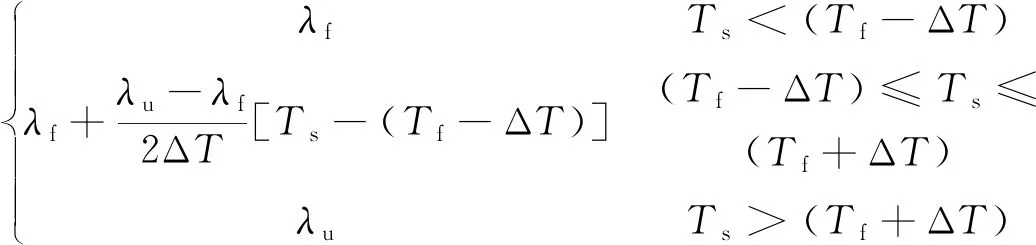
(6)

式中，Cf和Cu分别为隧道围岩在冻结状态和融化状态时的体积比热容，J·m-3·K-1；λf和λu分别为隧道围岩在冻结状态和融化状态时的导热系数，W·m-1·K-1；L为单位体积围岩相变潜热，J·m-3。

边界条件如下。

(1)流体边界条件为

u|A1=u0

(7)

如果边界为固体

u|A2=0

(8)

(2)温度边界条件为

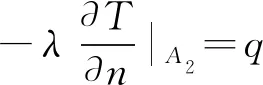
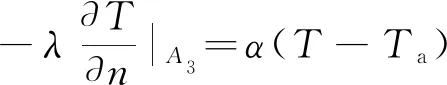
(9)

式中，Ai表示边界；T0为已知的确定温度，K；u0为已知的确定风速，m·s-1；λ为导热系数，W·m-1·K-1；n为各边界的法向矢量；q为热流密度，W·m-2；α为对流换热系数，W·m-2·K-1；Ta为空气温度，K。

如果为流-固耦合界面，定义固体界面对于黏性流体为无滑移边界，考虑到流体温度与固体温度连续，则有

T|A4+=T|A4-

(10)

初始条件如下。

(1)流场初始条件

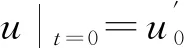
(11)

(2)温度初始条件

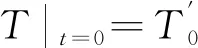
(12)

式(1)～式(12)组成了自然风条件下考虑围岩冰-水相变的寒区隧道空气与衬砌热交换和衬砌-围岩热传导的热流固耦合模型，以及边界条件和初始条件。将节点温度T、空气压力p和空气流动速度u作为基本未知量，运用隐式欧拉向后差分法(BDF法)对控制方程中的时间项进行离散，采用非线性迭代修正阻尼牛顿法求解方程。利用有限差分时间步长的方法，对该微分方程进行时间差分，并通过连续线性循环解法求解。

2.2.1 计算模型

考虑隧道贯通后，进入隧道内的冷空气和隧道衬砌壁面会发生强烈的热交换，从而改变围岩的温度场。因此，必须考虑隧道所在的整个山体内部热能影响下的温度分布，在此基础上，计算和分析自然风条件下隧道围岩的温度分布规律。以榆树川隧道上覆整个山体以及隧道下部80 m范围内的岩体作为研究对象，具体模型如图8所示。

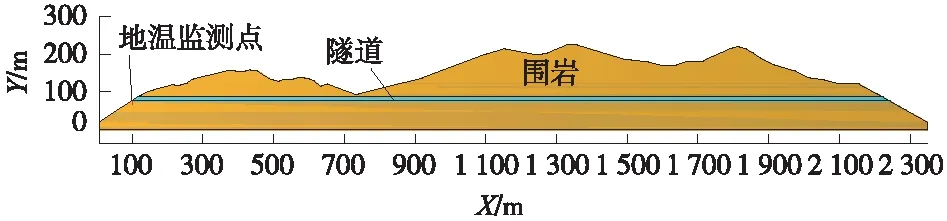
图8 计算模型

2.2.2 计算参数与边界条件

采用TPS2200热物性分析仪对隧道围岩和衬砌的导热系数和比热容进行测量，如图9所示。为精确得到不同温度时岩样的导热系数和比热容，测定实验在恒温箱中进行。无论是测量冻结状态还是融化状态围岩的热物理参数，测试开始前均将样品置于恒温箱中达到足够的温度恒定(3～5h)后，方能进行测定。测定的榆树川隧道围岩和衬砌的热物理参数如表1所示。

图9 隧道围岩和衬砌热物理参数测试装置示意

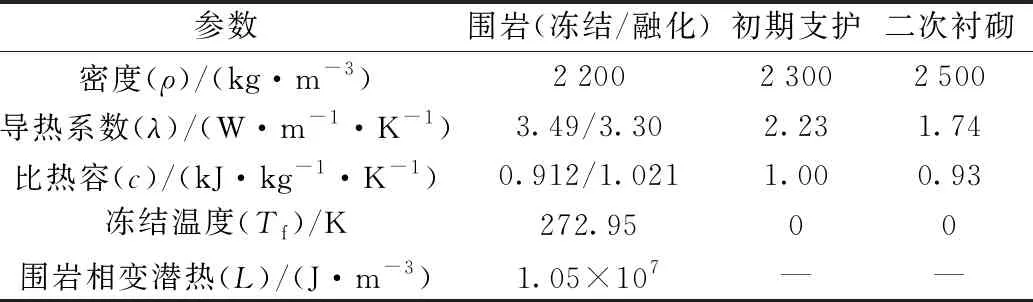
表1 围岩和衬砌热力学参数

空气的密度ρa为1.293 kg·m-3，导热系数λa和比热容ca分别为0.023 W·m-1·K-1和1.004 kJ·kg-1·K-1，空气动力黏度μ为1.75×10-5Pa·s。

整个计算模型(图8)中，两侧边界为绝热边界；模型底部的热流密度为0.06 W·m-2；空气与山顶的对流换热系数为15.0 W·m-2·K-1。隧道贯通后，隧道进口处空气速度为年平均风速，空气温度为大气温度。

3 计算结果与分析

3.1 模型验证

在榆树川隧道进口处，对自地表至深度10 m范围内天然地层的地温进行了监测。为验证建立模型的正确性，将地温监测数据与数值计算结果进行对比，如图10所示。通过对比2019年4月15日和2019年10月15日的地温实测值和计算值，可以看出：地温计算值与实测值沿深度变化规律一致。除地表至深度为-5 m范围内地温计算值与实测值有偏差外，其他位置温度计算值与实测值基本相同。地温计算值与实测值偏差较大处位于深度-2～-3 m处，最大温度差为0.8 ℃。造成地温计算值与实测值存在偏差的原因是浅层地表地温易受到外界环境的影响，而数值计算时采用温度边界条件忽略了环境条件变化的偶然性。通过比较地温的计算值和实测值，说明建立的传热模型能够反映隧道围岩的温度分布。

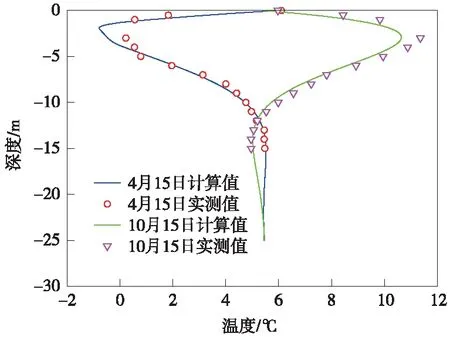
图10 地温实测值与计算结果对比

3.2 隧道贯通前山体温度场

隧道贯通前，以隧址整个山体为计算模型，模型底部施加热流密度0.06 W·m-2，空气与山体表面以对流换热方式传热，对流换热系数为15.0 W·m-2·K-1，模拟计算500年的传热过程。待山体温度达到稳定，以此作为隧道贯通前的隧址山体温度场。因隧址最低气温出现在1月份，最高气温出现在7月份，故分别以隧址山体1月、7月的温度分布来分析不同季节隧址山体温度场，如图11所示。由图11可以看出，隧道贯通前，隧址山体表层岩土体温度随季节波动，1月份表层岩土体发生冻结，最大冻结深度为1.6 m，7月份表层岩土体已经完全融化。除表层很小范围内的岩土体温度随季节波动外，山体大部分岩土体处于正温状态，温度不随季节的变化而变化，且大致在6～8 ℃内。进口段沿隧道纵向进深不超过70 m范围内围岩温度处于6 ℃以下，其余位置的岩温大于6 ℃。因上覆岩土体厚度不同，围岩温度略有差异。埋深分别为100 m和140 m处，隧道所在位置围岩温度分别为6.5 ℃和7.6 ℃。

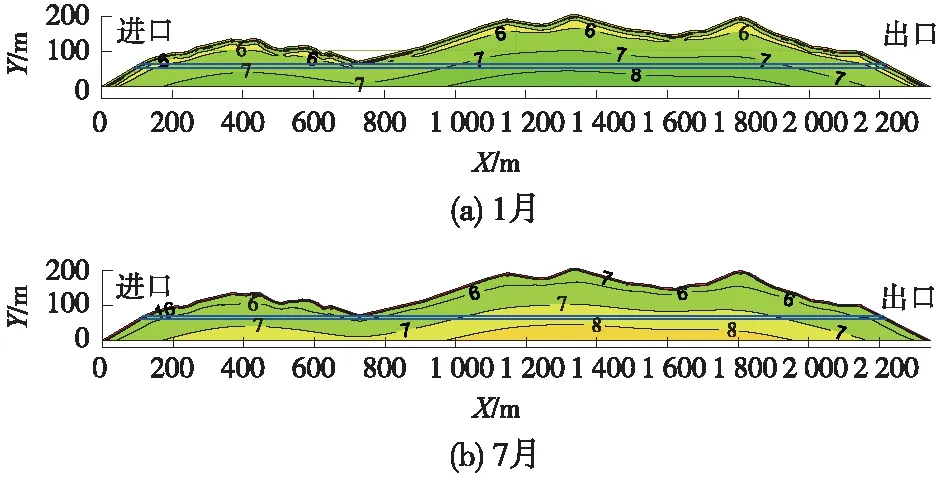
图11 不同季节隧址山体温度场分布(单位：℃)

3.3 自然风条件下隧道温度场

隧道贯通后，由于隧道进口和出口存在气压差，洞外的空气进入隧道内部，并与衬砌壁面发生热交换。风速越大，进入隧道内的空气越多，对隧道围岩温度场的影响也越大。以上节计算得到的隧道贯通前的山体温度场为初始温度场，在隧道进口处施加自然风速度和空气温度，以此计算隧道贯通后衬砌和围岩的温度分布。

考虑到隧道进口处平均风速为2.08 m/s，最大风速为5.44 m/s，分别对不同风速条件下(2.0，4.0，6.0 m/s)，最冷月(1月份)隧道围岩的温度场进行分析。由于隧道较长，为便于比较不同风速条件下隧道围岩温度场的分布规律，现截取计算结果中隧道进出口段一定范围内围岩和空气温度分布进行分析，如图12、图13所示。

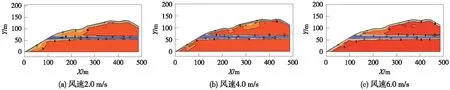
图12 榆树川隧道进口段1月份温度分布(单位：℃)

图13 榆树川隧道出口段1月份温度分布(单位：℃)

隧道贯通后，进入隧道的空气对围岩温度的影响显著，距离隧道衬砌很近的岩温已经明显降低。以岩温6 ℃等温线为例，隧道尚未贯通时，1月份进口段围岩温度不超过6 ℃的区域距离隧道进口约70 m(图11(a))；隧道贯通后，隧道进口段岩温小于6 ℃的区域扩大，当风速为2.0 m/s时，进口段该区域长度为203 m；当风速为4.0 m/s时，区域长度为242 m；而当风速增大到6.0 m/s时，区域长度增大到315 m(图12)。同样地，隧道贯通后，隧道出口段距离衬砌很近的围岩也已处于冻结状态，同时出口段岩温小于6 ℃的区域也扩大，当风速为2.0 m/s时，该区域长度为49 m，当风速为4.0 m/s时，区域长度为67 m；而当风速增大到6.0 m/s时，区域长度增大到76 m(图13)。综合不同风速作用下隧道进出口段的围岩温度分布可以得到：隧道贯通后，进入隧道空气的温度对围岩的温度分布影响很大，在洞外空气温度最冷月(1月份)，隧道进出口段靠近衬砌的围岩均发生了冻结，这意味着隧道进出口段需施作相应的防冻保温措施。

3.4 隧道冻结长度

隧道贯通后，不同风速条件下(2.0，4.0，6.0 m/s)，洞外空气温度最冷月(1月份)衬砌温度沿隧道纵向分布曲线如图14所示。由图14可以看出，当隧道进口段风速为0 m/s时，空气温度对隧道的影响非常有限，进口段冻结长度为6.14 m。随着风速增大，进入隧道的冷空气增多，冻结长度也不断增大。当风速分别为2.0，4.0，6.0 m/s时，进口段冻结长度分别为707，1 037，1 527 m。同时，进口段风速的增加对隧道出口段衬砌温度的影响较小，出口段冻结长度在27～36 m内，且隧道进口段的冻结长度远大于出口段，这与现场监测结果(进出口段冻结长度分别为1 443 m和29 m)非常相似，这也说明自然风对隧道进出口段冻结长度的影响不相同。

图14 不同风速作用下衬砌温度沿隧道纵向分布曲线

通过以上分析可以看出，隧道洞外风速对隧道温度场的分布影响显著，为确定不同风速作用下隧道的冻结长度，现计算得到了隧道进出口段最大冻结长度随风速的变化，如图15所示。分别将不同风速作用下的进出口段的冻结长度计算值进行拟合，得到了隧道两端冻结长度与风速的关系，隧道两端冻结长度均随着风速的增大呈线性增大趋势，寒区隧道冻结长度应考虑进口段风速的大小，盲目地采取隧道全长范围内施作防冻保温措施是不经济的。当风速为0 m/s时，隧道进口段冻结长度计算值与拟合值偏差较大(计算值为6.14 m，拟合值为83.6 m)，而当风速变大后，冻结长度计算值与拟合值相差不大(风速为1 m/s时，计算值和拟合值分别为296.6，318.3 m)。这是由于风速较小时，隧道内空气热传导以自然对流为主，当风速较大时，热传导方式以强迫对流为主，而拟合得到的风速与冻结长度的关系多是基于强迫对流的结果。但是，风速较小时冻结长度的拟合值比计算值大，这在工程上对防止隧道围岩发生冻结是有利的。这说明拟合得到的风速与隧道进、出口段冻结长度的关系可以对寒区隧道防冻提供有益指导。同时，由图15也可以看出，风速对隧道进出口段的影响不同，相同风速条件下，隧道进口段的冻结长度比出口段冻结长度大得多，这意味着考虑经济性的情况下，隧道进出口段施作防冻保温措施应有所不同。

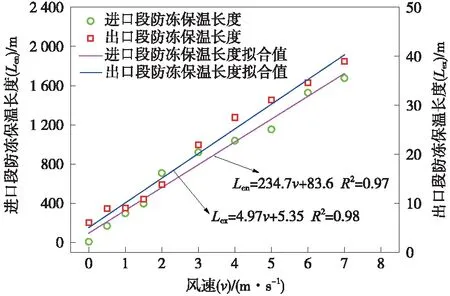
图15 不同风速下隧道进口段和出口段冻结长度

4 结论

根据吉图珲高速铁路榆树川隧道的气温、风向和风速，建立了自然风条件下考虑围岩冰-水相变的榆树川隧道空气与衬砌热交换和衬砌-围岩热传导的热流固耦合模型，得出以下结论。

(1)榆树川隧道贯通前，除进口段和出口段沿隧道纵向进深1.6 m范围内的围岩温度受环境影响波动较大(寒区冻结，暖季融化)，其余绝大部分隧道位置处的围岩温度处在6～8 ℃内。

(2)榆树川隧道贯通后，冷空气进入隧道后与衬砌发生强烈的热交换，影响围岩温度场的分布，进出口段岩温明显降低，距离衬砌很近处围岩发生冻结。随着风速的增大，隧道进口段冻结长度不断增大，隧道进出口段需施作相应的防冻保温措施。

(3)随着进口段风速的增加，进入隧道的冷空气增多，空气温度对隧道温度场的影响也愈加显著。隧道进出口段冻结长度均随着风速的增大呈线性增大趋势，当自然风从隧道进口吹入，从出口吹出，风速对进口段冻结长度的影响程度远大于出口段。隧道冻结长度应根据隧址气温和风速进行确定，在考虑经济性的情况下，隧道进口段与出口段施作防冻保温措施应有所不同。