高速铁路300 m以上跨度桥梁线形评价标准研究
2021-09-26魏周春苏成光
刘 超,魏周春,张 岷,苏成光
(1.中铁第一勘察设计院集团有限公司,西安 710043; 2.陕西省铁道及地下交通工程重点实验室(中铁一院),西安 710043)
1 研究背景
随着我国高速铁路技术水平不断发展,300 m级跨度桥梁建设越来越多。国内第一座主跨300 m桥梁-昌赣高铁赣江特大桥[1-2],采用斜拉桥结构;已建成通车最大跨度桥梁-商合杭铁路裕溪河特大桥[3],主跨324 m,采用斜拉桥结构。新建南宁至玉林铁路设计时速350 km,正线采用CRTS双块式无砟轨道。项目沿线区域水系发达,受线路周边环境和河流通航要求设百合郁江特大桥,主桥为(36+40+64+330+64+40+36) m双塔双索面钢-混凝土混合梁斜拉桥结构,主跨330 m。主桥跨中306 m范围为钢箱梁,两侧各设过渡区7 m,其余地段为混凝土梁,桥梁立面如图1所示。桥梁左侧主塔位置设置固定支座,桥塔采用钻石形钢筋混凝土塔,空心矩形截面。桥梁所在平面为直线,竖向设置2‰“人”形纵坡,跨中竖曲线范围为100 m,竖曲线半径为25000 m。
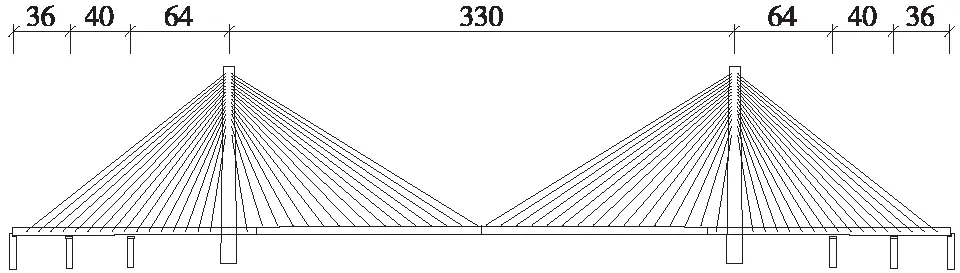
图1 百合郁江特大桥立面(单位:m)
目前研究表明[4-8],高速铁路大跨度桥梁结构面临的主要问题是,在温度和列车荷载作用下,竖向变形远超过不平顺管理值。当桥梁主跨超过300 m,跨中竖向挠曲变形往往超过200 mm。无砟轨道对下部变形适应性差,桥梁变形将直接映射在钢轨面上,使轨道结构高低不平顺超限。针对这一问题,李秋义等[3]提出大跨桥轨面线形控制应按照不均匀沉降处理;褚卫松等[9]通过建模分析,建议将长波不平顺管理弦长值调整至115 m;李闻秋、秦艳等[10-15]对特殊大跨桥-无砟轨道系统的适用性进行了研究。
综合来看,大跨桥结构的桥梁-轨面变形和控制方法、桥梁变形线形评价分析,尚未形成统一的研究思路和评判标准。既有成果较为单一、线形评价标准不够完善,有必要对此开展研究。
2 工况选择及荷载组合
大跨斜拉桥结构在服役中的竖向变形影响因素主要包含:桥梁结构整体温变、斜拉索和梁面温差、结构收缩徐变、桥梁面板不均匀温差、左右侧拉索不均匀温差及列车荷载等。理论计算时整体温变一般取±25 ℃、索温差取10 ℃、桥梁面板不均匀温差取10 ℃、左右侧拉索不均匀温差取5 ℃,列车荷载按实际列车轴重取值。
本次开展研究的大跨度斜拉桥在不同单项工况影响下的桥梁变形量如图2所示。可以看出,变形量的主要影响因素可划分为温度荷载、列车荷载和桥梁收缩徐变三类。参考既往研究经验,不同荷载作用幅度有所不同,通过单纯叠加所有荷载作用计算轨面的最大变形量并不合理。依据TB 10002—2017《铁路桥涵设计规范》[16]计算桥梁挠跨比时思路,将列车荷载和温度荷载的取值系数进行组合,同时兼顾收缩徐变影响,使研究工况更贴合实际桥梁所处环境(工况1、工况2、工况4、工况5);此外,对所有单项上拱工况和下挠工况进行叠加,选取计算最不利变形(工况3、工况6)开展对比研究。工况组合取值系数如表1所示,工况组合方式见式(1)。
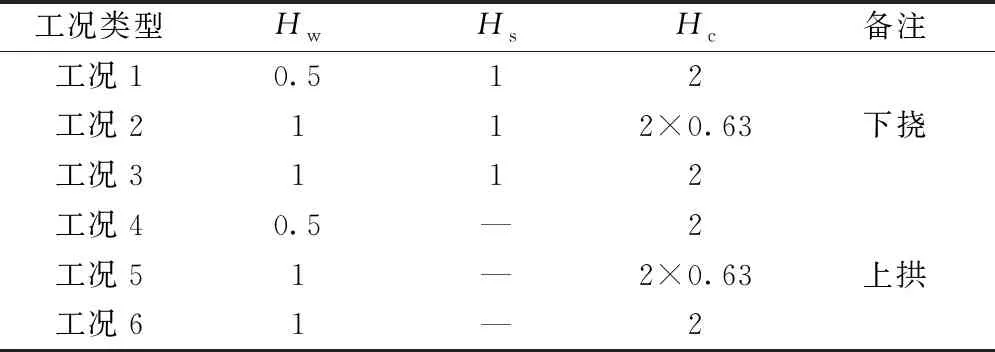
表1 主要工况组合系数
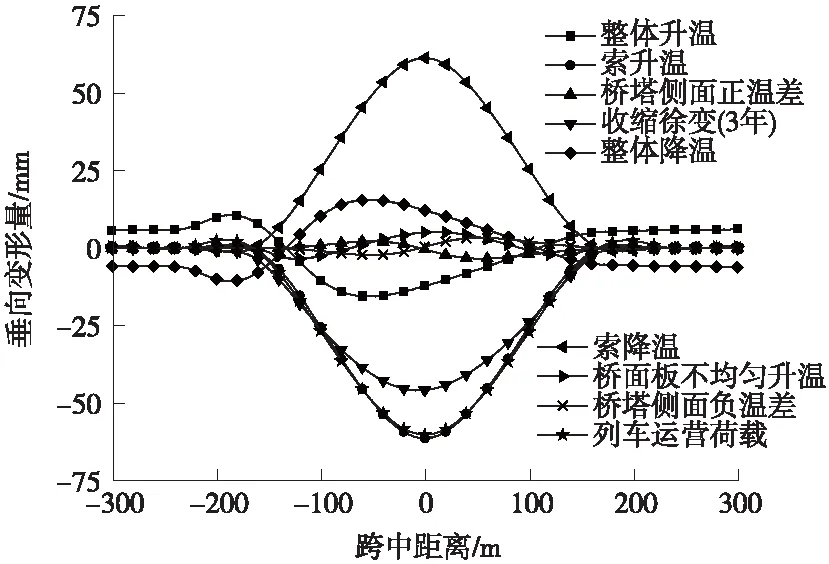
图2 主要工况影响下梁面变形量
工况X=温度荷载×Hw+收缩徐变×Hs+列车荷载×Hc
(1)
3 线形评价研究
3.1 60 m弦测评价法
基于中点弦测法的不平顺计算原理如图3所示。假定测量弦长为2L,测量i点时,需要同时测量i-L点和i+L点,则i点的不平顺幅值为
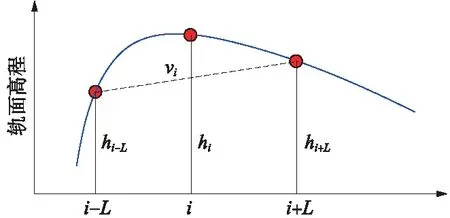
图3 中点弦测法示意
(2)
式中,vi为i点不平顺幅值;hi为i点轨面高程;hi-L及hi+L为i点前后Lm位置轨面高程。
依据TG/GW 115—2012《高速铁路无砟轨道线路维修规则(试行)》[17]中车体振动加速度的控制标准,结合《运营期高铁轨道平顺性提升关键技术研究报告》[18]的相关研究成果,基于中点弦测法的350 km/h线路轨面不平顺测量弦长宜控制在60 m,超限控制标准如表2所示。

表2 不同等级60 m弦测法控制标准
采用60 m弦测评价法计算桥梁结构在不同工况下变形的不平顺幅值,如图4所示。
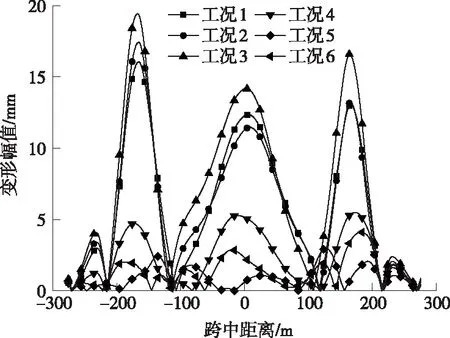
图4 各工况60 m弦测不平顺幅值曲线
从图4可以看出:所有工况均未超出Ⅳ级限值要求,不会因线路平顺性而限速;升温工况影响下,墩台处(横坐标±165 m)弦测幅值更加明显,不平顺更为剧烈;降温工况影响下,线路平顺性较升温工况条件更优,变形量更小。
3.2 竖曲线半径评价法
实际大跨桥结构在叠加线路设计竖曲线后,梁面线形是一条由多圆弧拼合而成的空间曲线。以工况3为例,荷载作用时实际梁面空间位置如图5所示。可以发现,实际梁面线形是由5个具有明显凹凸性的圆弧组合而成,因此,需要进一步寻找曲线凹凸性变化点来划分圆弧,进行竖曲线拟合。
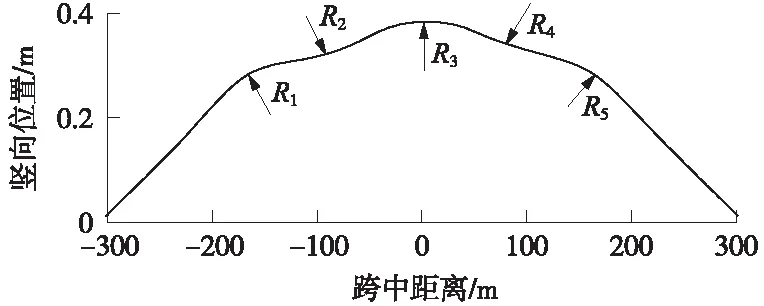
图5 实际梁面线形及预估竖曲线示意
由曲线二阶导数的相关数学意义可知,二阶导数表达一阶导数的变化率,反应图像的凹凸性,二阶导数0点即为图像凹凸性改变点。因此,可以通过曲线二阶导数正负确定每个圆曲线的具体范围,进一步拟合求其竖曲线半径。
经计算,求得工况3所对应的二阶导数曲线如图6所示。可以看出,主跨范围由6个二阶导数“零点”划分为5段圆弧曲线。进一步针对5段圆弧曲线进行拟合,求其竖曲线半径。

图6 工况3梁面线形曲线二阶导数
TB10621—2014《高速铁路设计规范》[19]规定:在350 km/h行车速度下,竖曲线最小半径为25 000 m,最大半径为30 000 m,允许发生的均匀沉降拟合竖曲线半径为49 000 m,因此可以采用三级竖曲线控制限值,如表3所示。

表3 不同拟合竖曲线控制标准
若将桥面线形分割为多条竖曲线,将会与《高速铁路设计规范》中关于最小坡段长规定产生冲突。但考虑最小坡段长度设置初衷是让前一个竖曲线上的车体振动和后一个竖曲线上的车体振动叠加,减小车体振动加速度,且在350 km/h速度下30 000 m竖曲线坡段差值为40‰,夹坡长度为0 m时,车体振动加速度峰值为0.965 m/s2,小于规范规定的0.985 m/s2标准要求。因此,在进行大跨桥跨中线形加速度分析时,不再考虑竖曲线夹坡长度和最小坡段长度影响。不同工况下拟合竖曲线半径计算结果如表4所示。

表4 不同工况拟合竖曲线半径 m
从表4可以看出:考虑线路设计线形,各工况作用下百合郁江特大桥实际线形的拟合竖曲线半径均大于困难限值标准;升温工况影响下,桥梁结构的最不利位置位于两墩台处,跨中叠加竖曲线变形后舒适度较好,可满足路基均匀沉降顺坡后相关规范要求;桥梁发生降温上拱时,线路的主要不平顺位于跨中,拟合竖曲线半径接近设计竖曲线半径。
3.3 旅客舒适度评价法
旅客舒适度评价法是一种基于车辆通过竖曲线时旅客所能接受加速度的能力来进行评价的方法。
实际梁面线形在空间内是一条复杂的连续曲线。列车通过桥梁时,若将车内乘客视为一个质点,则在空间曲线的每一个点上,乘客均能感受到一个离心加速度,而这个加速度可由质点所在位置的曲率半径求解。由于实际梁面线形是一条连续可微分曲线,因此,可以依据式(3)求曲线在每一点的曲率半径。
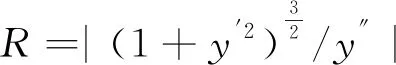
(3)
式中,R为曲率半径;y″为曲线一阶导数;y″为曲线二阶导数。
《高速铁路设计规范》条文说明中解释:竖曲线半径由旅客舒适性要求控制,即列车运营于竖曲线产生的竖向离心加速度ash限值的最小竖曲线半径,如式(4)所示。可以通过曲率半径和离心加速度的对应关系进一步换算为旅客质点通过桥梁每一点时旅客感受到的离心加速度。
Rsh≥v2/(3.62·ash)
(4)
式中,Rsh为竖曲线半径;ash为竖向离心加速度,一般情况下取0.4 m/s2,困难条件下取0.5 m/s2。
此外,《高速铁路设计规范》规定,路基地段发生均匀沉降,且拟合竖曲线的半径标准满足R≥0.4v2时,可认为其能满足正常行车需求,计算的对应离心加速度为0.19 m/s2。因此,对应加速度评价法限值如表5所示,各工况求解结果如图7所示。

表5 不同等级加速度控制标准
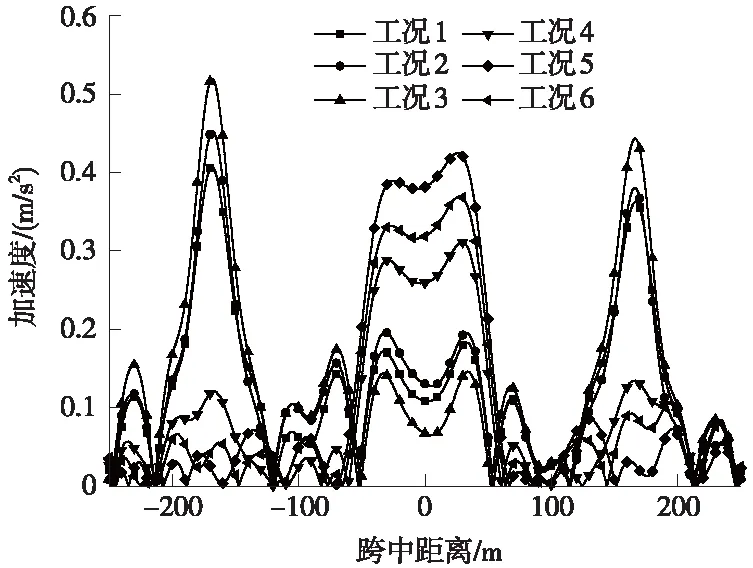
图7 各工况旅客加速度幅值曲线
从图7可以看出:工况3作用下,小里程墩台位置(横坐标-165 m)旅客加速度会超过困难限值,其余工况均能满足加速度的困难限值;升温工况影响下,桥梁结构的最不利位置位于两墩台处,跨中范围旅客舒适度较好,加速度均小于0.2 m/s2;桥梁发生降温上拱时,线路的主要不平顺位于跨中,旅客加速度小于0.4 m/s2。
4 动力仿真计算分析
结合车-线-桥耦合动力学理论与模态叠加法,建立三维耦合动力学模型。模拟极端温度荷载作用,桥梁结构发生极端竖向变形已经造成较大线路不平顺时,8列编组列车单线通过桥梁时的动力响应。
4.1 模型介绍
根据多体动力学理论,将车辆子系统模型简化为由7个刚体以及35个自由度组成的多刚体结构,如图8所示。
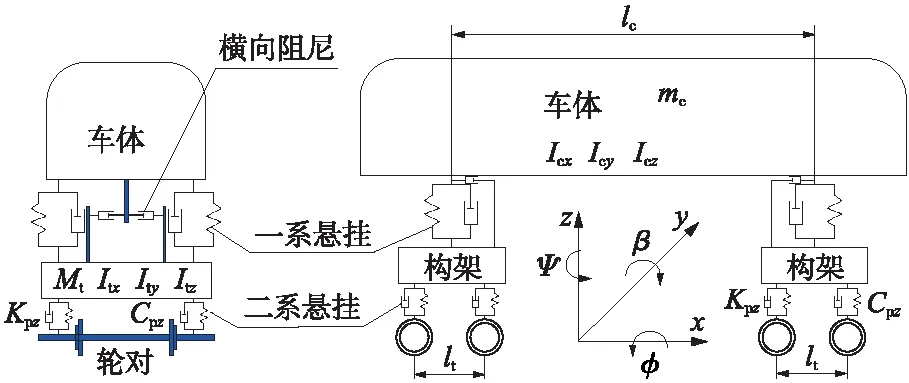
图8 车辆系统结构模型
轨道子系统采用无砟轨道结构,主要由钢轨、扣件、轨枕以及轨道板组成。其中,钢轨被视为连续弹性离散点支承上的无限长Euler梁,每个弹性支承单元采用双质量、三层(钢轨-轨道板-下部结构)弹簧-阻尼振动模型。
桥梁子系统采用有限元软件建立,如图9所示。考虑到桥梁的响应受到若干低阶模态控制,为提高效率,在与多体系统的耦合分析中,采用模态叠加法将位移向量从一般的物理空间转化到以模态向量为基向量的模态空间中,同时在梁面体现静态最不利变形的激励源。
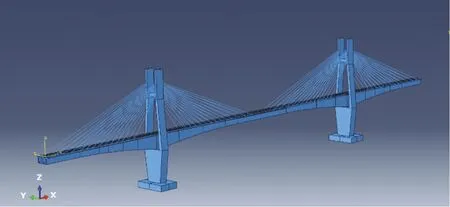
图9 桥梁结构模型
4.2 评价指标
列车运行安全性是铁路运输最基本的要求,分别采用轮轨垂向力、轮轨横向力、脱轨系数及轮重减载率对列车运行的安全性进行评价。
(1)轮轨垂向力
机车通过桥梁时,导向轮对每个车轮作用于轨道的垂向作用力峰值极限值Pmax=170 kN。
(2)轮轨横向力
选取CRH380型进行动力学仿真,其净轮重为61.3 kN,横向力限值为49.04 kN。
(3)脱轨系数
根据TB 10761—2013《高速铁路工程动态验收技术规范》[20]规定,脱轨系数应满足式(5)要求。
Q/P≤0.8
(5)
(4)轮重减载率
根据《高速铁路工程动态验收技术规范》规定,轮重减载率应满足式(6)的要求。
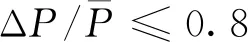
(6)
4.3 计算结果
依据工况3的计算最不利工况,动态仿真分析计算结果如图10所示。

图10 动力响应分析结果
由图10可以看出:在桥梁结构受整体温升(25 ℃)、索温差(10 ℃)、收缩徐变和其他温度荷载综合作用下,发生极端竖向变形时,列车以350 km/h速度通过桥梁结构,此时车体各项动力学指标均能满足相关标准要求。
5 结论
结合百合郁江特大桥实际变形工况,对桥梁变形条件下列车350 km/h行车速度适应性开展分析,主要结论如下。
(1)在线形分析时应充分考虑各种荷载出现的概率,单项工况宜进行合理组合以真实模拟实际情况。
(2)60 m弦测评价法、竖曲线半径评价法、旅客舒适度评价法均能较好地对梁面线形进行评价分析。百合郁江特大桥跨中位置在各项评价标准下均能较好满足控制标准,平顺性较墩台位置更佳。
(3)极端静态工况作用时,双线列车同时经过跨中,会造成墩台位置评价指标超限,应加强桥梁结构细部设计并在运营期加强墩台处变形监控。
(4)从动力学计算结果来看,当梁面线形发生最不利温度荷载变形时,列车动力学响应较好,各项指标均满足行车需求。
