前混合空化水射流解离鳞片石墨的微射流冲击特性

董 星， 郭忱灏， 孙永猛

(1.黑龙江科技大学 机械工程学院， 哈尔滨 150022； 2.潍坊理工学院 新松机器人学院， 山东 潍坊 262500)

0 引 言

石墨具有导热、导电、耐高温、韧性好等优良性能，是重要的战略资源[1-2]。鳞片石墨又称为晶质石墨，其性能均优于其他类型石墨，因此广泛应用于诸多国民经济领域[3]。空化水射流是指利用空化气泡溃灭产生的冲击力增强射流效果的混合水射流[4-5]。空化气泡初生和发展阶段会累积大量势能，在空泡溃灭时会释放出大量动能，达到空蚀破坏的效果，具体体现在高速微型射流。射流空化的全过程包括空泡的孕育与初生、发育与长大、收缩和溃灭。高压区溃灭空泡产生的高速微射流及强烈的冲击波，造成材料损伤[6]。为有效利用空化形成的微射流冲击效应，学者们通过理论分析、数值模拟等方法进行了相关研究，取得了相应研究成果[6-12]，但对微射流解离鳞片石墨的研究鲜见报道。笔者采用ANSYS/LS-DYNA软件对前混合空化水射流形成的微射流冲击鳞片石墨过程进行数值模拟，分析了微射流加载时间对射流解离鳞片石墨效果和冲击速度衰减规律的影响，获得了冲击载荷作用下的石墨靶体应力状态及表面形貌特征，为微射流解离鳞片石墨奠定技术基础。

1 基本模型与计算方法

1.1 几何模型

根据前混合空化水射流解离的鳞片石墨颗粒实际情况，将鳞片石墨颗粒靶体简化为长方体，其尺寸为0.15 mm×0.10 mm×0.04 mm；将空化水射流形成的微射流简化为前端是半球体、后端是圆柱体组成的轴对称结构体。取轴对称结构体的一半为研究对象，微射流半球体的半径为0.013 mm，微射流总高度为0.039 mm。根据前混合空化水射流冲击鳞片石墨颗粒靶体的对称性，采用Pro/E软件建立的二维几何模型如图1所示。

图1 几何模型Fig. 1 Geometric model

1.2 有限元模型

根据几何模型的结构特点，利用ANSYS/LS-DYNA软件模拟前混合空化水射流冲击鳞片石墨颗粒靶体时采用二维平面轴对称算法。网格类型选用具有4自由度的对称算法LS-DYNA Explicit 2D Solid 162单元，微射流采用ALE网格，鳞片石墨靶体采用Lagrange网格[11-12]。微射流划分的单元数为512个，鳞片石墨靶体划分的单元数为2 400个，划分网格后的有限元模型如图2所示。

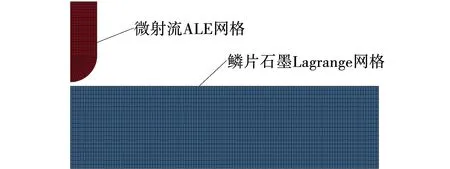
图2 有限元模型Fig. 2 Finite element model

1.3 数学模型

1.3.1 流体控制方程

采用ANSYS/LS-DYNA中的ALE算法对微射流冲击鳞片石墨进行数值模拟。ALE算法充分结合了Lagrange和Eulerian有限元的优越性，解决了Lagrange描述下材料可能存在严重扭曲的问题，ALE算法的流体控制方程分别对应质量守恒方程、动量守恒方程、能量守恒方程[13]：

(1)质量守恒方程

(1)

式中：ρ——物质的密度；

t——时间；

p——物质的压力；

vi——物质的速度矢量分量；

wi——物质的相对速度。

(2)动量守恒方程

(2)

σij=-pδij+μ(vi·j+vj·i)，

(3)

式中：v——物质的速度；

σij——应力张量；

bi——单位质量的体力。

(3)能量守恒方程

(4)

式中，E——物质的能量。

1.3.2 材料模型

微射流冲击鳞片石墨过程中，水被认为是完全塑性材料且始终处于压缩状态，因此，选择Grunreisen方程作为水的状态方程，Grunreisen状态方程定义压缩材料压力[13-14]为

(γ0+aμ)E，

(5)

式中：ρ0——压缩材料的密度；

C——冲击速度变化曲线的截距；

S1、S2、S3——冲击速度变化曲线的斜率系数；

γ0——Gruneisen常数；

a——γ0和μ的一阶体积修正量；

μ——压缩度。

靶体材料为鳞片石墨，石墨材料抵抗外力的能力为石墨的强度，表征石墨强度的性能指标有抗拉强度、抗压强度和抗剪强度，鳞片石墨的抗拉强度为7 MPa，抗压强度为20 MPa[15]。石墨靶体内部存在或经外载荷作用产生微裂纹，在冲击外力作用下，微裂纹经发展、延伸、扩大，直至引起石墨材料的断裂，而石墨材料的抵抗裂纹扩展的能力为断裂韧性，它也是影响鳞片石墨解离的重要因素之一。

1.4 载荷及边界条件

空化水射流冲击鳞片石墨过程是由高压泵产生高压水，经空化喷嘴产生空化水射流，空化发生形成的微射流以很高的速度对鳞片石墨表面施加冲击载荷，载荷的施加通过定义微射流初始冲击速度的方式实现。

微射流冲击载荷作用于鳞片石墨靶体模型上表面沿y轴负方向，因此对模型的下表面进行完全的自由度约束，限制模型下表面的移动和转动；模型上的其他节点具有4个方向自由度，位移不被约束。

2 模拟结果与分析

2.1 加载时间对射流解离效果的影响

图3给出了微射流以400 m/s冲击速度、加载时间分别为5、11、15、39、55、80 μs时冲击鳞片石墨靶体在靶体轴平面上产生的径向应力分布云图。由图3可见，微射流加载时间分别为5、11、15、39、55和80 μs时，靶体轴平面上产生的最大径向拉应力分别为0.017、3.783、7.893、5.978、5.695和5.678 MPa。

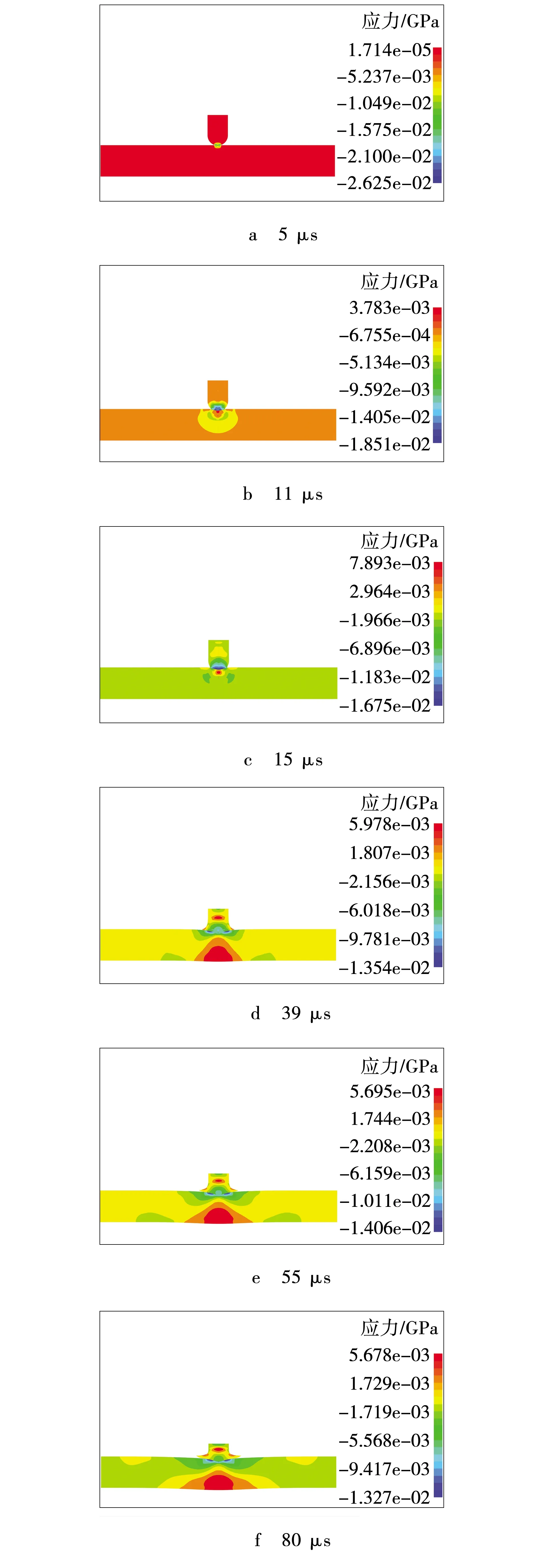
图3 靶体径向应力分布云图Fig. 3 Radial stress contour of target body

当微射流加载时间分别为5、11 μs时，加载时间较短，石墨靶体中未形成足够的冲击载荷，因此靶体中产生的径向拉应力较小，加载11 μs时产生的最大径向拉应力仅为3.783 MPa。当加载时间为15 μs时，加载时间延长，石墨靶体中形成了足够的冲击载荷，在靶体中产生的最大径向拉应力为7.893 MPa，出现在射流冲击轴线下的一定深度处，大于石墨的抗拉强度7 MPa，石墨靶体遭到破坏，产生裂纹，并在石墨靶体表面出现凹坑。当加载时间为39 μs时，加载时间进一步延长，遭到破坏产生裂纹的石墨靶体承载能力下降，在靶体中产生的最大径向拉应力相应减小，为5.978 MPa，但靶体中的裂纹继续扩展，靶体表面的凹坑继续增大，最终在石墨靶体表面形成“火山口”型的冲击凹坑。当加载时间分别为55、80 μs时，在靶体中产生的裂纹进一步扩展，靶体表面的凹坑继续增大；同时，微射流沿靶体表面产生较大的径向流动，径向流动在靶体表面产生剪切效应，拉应力和剪应力的共同作用会加速石墨靶体的破坏，最终使石墨靶体在最弱的结合面处产生解离破坏。

图4给出了微射流以400 m/s速度、加载时间分别为5、11、15、39、55、80 μs时冲击鳞片石墨靶体在靶体轴平面上产生的轴向应力分布云图。由图4可见，微射流加载时间分别为5、11、15、39、55和80 μs时，靶体轴平面上产生的最大轴向压应力分别为29.15、24.67、21.87、14.73、14.03和11.59 MPa。

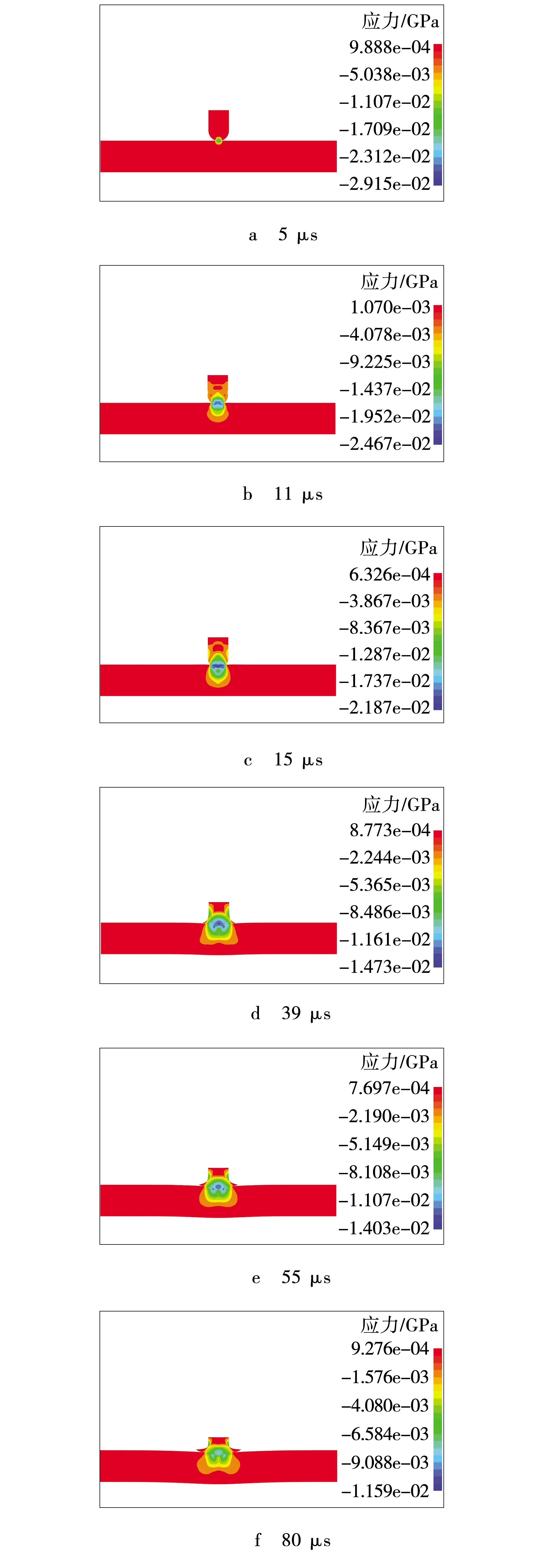
图4 靶体轴向应力分布云图Fig. 4 Axial stress contour of target body

当加载时间在5～15 μs范围时，在靶体中产生的最大轴向压应力均大于石墨的抗压强度20 MPa，石墨靶体遭到破坏产生裂纹，并在靶体表面出现冲击凹坑。当加载时间为39 μs时，遭到破坏产生裂纹的靶体承载能力下降，在靶体中产生的最大轴向压应力相应减小至14.73 MPa；靶体表面的裂纹继续扩展，靶体表面的冲击凹坑继续增大；另外，嵌布脉石与石墨结合面上存在着较弱的结合力，若微射流作用在嵌布脉石与石墨的结合位置时，嵌布脉石受到微射流冲击产生的压应力、水楔效应产生的拉应力的共同作用将从石墨靶体表面剥离。当加载时间分别为55、80 μs时，遭到破坏产生裂纹的靶体承载能力继续下降，在靶体中产生的最大轴向压应力继续减小，但靶体表面的裂纹继续扩展、冲击凹坑继续增大；同时，微射流沿靶体表面产生较大的径向流动，径向流动在靶体表面产生剪切作用，嵌布脉石受到微射流冲击产生的压应力、水楔效应产生的拉应力和射流径向流动产生的剪应力的共同作用，将加速嵌布脉石从石墨靶体表面剥离。

2.2 加载时间对冲击速度衰减规律的影响

为研究微射流冲击鳞片石墨靶体过程中加载时间对冲击速度衰减规律的影响，以微射流几何模型半球顶点为研究对象，分析微射流初始冲击速度分别为300、400、500、600、700 m/s，全程加载时间为80 μs时微射流冲击速度随加载时间的变化规律。

图5给出了微射流初始冲击速度分别为300、400、500、600、700 m/s时，微射流冲击速度随加载时间的变化曲线(由于y坐标轴向上设置，所以图5纵坐标速度刻度前冠以负号)。

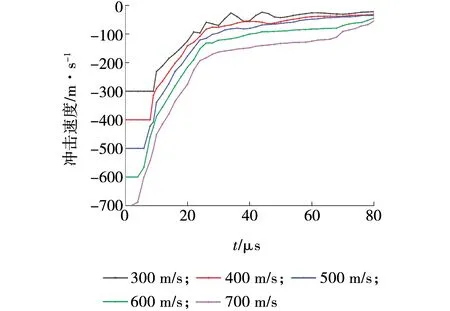
图5 冲击速度随加载时间的变化曲线Fig. 5 Curve of impact velocity versus loading

由图5可见，随着射流加载时间的增加，不同微射流冲击速度随加载时间的速度变化规律相同，速度曲线变化过程均可以分为3个阶段：第1阶段为水平直线段，即微射流从喷嘴喷出至刚接触石墨靶体表面的加载时段，射流速度保持不变，等于射流初始冲击速度，射流速度曲线为一条水平直线。第2阶段为速度梯度较大的近似直线段，即随着微射流与石墨靶体接触加载时间的增加，由于石墨靶体的非金属脆性材料的力学性能，射流受到石墨靶体的抗力迅速增大，射流冲击速度急剧下降，直至石墨靶体遭到破坏产生裂纹，射流速度出现转捩点，该段射流速度曲线为一条速度梯度较大的近似直线。第3阶段为速度梯度较小的近似直线段，即随着微射流与石墨靶体接触加载时间的继续增加，遭到破坏产生裂纹的石墨靶体承载能力急剧下降，射流受到石墨靶体的抗力迅速减小，射流冲击速度下降明显变缓，直至微射流冲击速度衰减逐渐趋向于零，该段射流速度曲线为一条速度梯度较小的近似直线。

另外，不同的初始冲击速度300、400、500、600和700 m/s时，对应的速度曲线的第1阶段、第2阶段和第3阶段的加载时间亦不同。初始冲击速度分别为300、400、500、600和700 m/s时，第1阶段的加载时间范围分别为0～7.6、0～4.8、0～3.8、0～2.7和0～0.8 μs；第2阶段的加载时间范围分别为7.6～35.4、4.8～27.9、3.8～24.9、2.7～22.8和0.8～20.7 μs，该阶段加载结束时射流冲击速度衰减分别减小至39.1、76.2、115.2、151.4和225.8 m/s；第3阶段的加载时间范围分别为35.4～80、27.9～80、24.9～80、22.8～80和20.7～80 μs，该阶段加载结束时射流冲击速度衰减分别减小至22.2、28.7、34.4、35.8和37.6 m/s。

由此可知，随着初始冲击速度的增加，第1阶段射流从喷嘴喷出至开始接触石墨靶体所需时间逐渐减小，分别为7.6、4.8、3.8、2.7、0.8 μs。第2阶段射流与石墨靶体开展接触，石墨靶体的抗力迅速增大至石墨靶体遭到破坏产生裂纹过程的加载时间亦逐渐减小，分别为27.8、23.1、21.1、20.1和19.9 μs。说明微射流冲击速度越大，石墨靶体抵抗射流冲击，遭到破坏产生裂纹所需时间越短，就越有利于微射流对鳞片石墨的解离，但初始冲击速度在600 m/s及以上时，这种速度载荷效应明显减弱。第3阶段石墨靶体遭到破坏产生裂纹、射流速度出现转捩点至加载80 μs结束，射流加载时间逐渐延长，分别为44.6、52.1、55.1、57.2和59.3 μs。说明微射流冲击速度愈大，石墨靶体遭到破坏产生裂纹的承载能力下降愈快，射流速度出现转捩点的时间愈短，在该阶段射流对石墨靶体持续冲击时间愈长，因此射流持续冲击所产生的拉应力和剪应力的共同作用进一步提高了解离鳞片石墨效果。

3 结 论

(1)当微射流冲击速度为400 m/s、加载时间为15 μs时，射流冲击在鳞片石墨中产生的最大径向拉应力为7.893 MPa，大于鳞片石墨的抗拉强度，鳞片石墨发生破坏。

(2)微射流冲击在鳞片石墨靶体中产生压应力，当产生的最大轴向压应力大于鳞片石墨的抗压强度时，鳞片石墨发生破坏；同时压应力的作用在鳞片石墨靶体表面产生冲击凹坑，随着加载时间的增加冲击凹坑逐渐增大。

(3)鳞片石墨发生破坏产生裂纹，随着加载时间的增加，在微射流持续冲击作用下鳞片石墨靶体承载能力急剧下降，射流受到石墨靶体的抗力迅速减小，最终实现鳞片石墨的解离。

(4)不同冲击速度随加载时间变化的衰减规律相同，速度曲线变化过程分为水平直线段的第1阶段、速度梯度较大的近似直线段的第2阶段和速度梯度较小的近似直线段的第3阶段，初始冲击速度愈大愈有利于射流冲击解离鳞片石墨。