配电网与蓄热式电采暖负荷的优化匹配策略
2021-09-25董晓颖郭浩波
董晓颖,李 拓,苏 娟,郭浩波,屈 博
(1.中国农业大学 信息与电气工程学院,北京 100083;2.中国铁道科学研究院,北京100081;3.中国电力科学研究院有限公司,北京 100192)
0 引言
为实现“碳达峰、碳中和”目标,目前我国推行“以电代煤”。蓄热式电采暖作为可中断、可转移的灵活性负荷资源,与直热式电采暖相比更有优势。因此需要进行蓄热式电采暖负荷与配电网台区匹配技术的相关研究,以真正实现停电不停暖、减小电网运行压力的目标。随着智能电网技术的逐步发展,电力需求响应已成为双向交互式智能电网框架下的一种重要的交互式响应方法[1]。目前,国内外学者对直热式电采暖负荷参与削峰填谷进行了研究。
优化控制策略是指根据需求侧管理策略优化采暖行为,使电采暖负荷与电网相匹配。可将目标曲线与规划曲线之差的均方根值和标准差作为衡量目标曲线与规划曲线匹配程度的指标[2]。文献[3]构造了基于负荷波动程度的目标函数,采用有序用电调控参与响应的用户,得到了日最佳参与率和最优激励政策。对于温控负荷,多数研究采用直接负荷控制(direct load control,DLC)策略。文献[4]提出了一种兼顾降负荷和反弹抑制的负荷聚合商下空调集群调控策略。文献[5]考虑了负荷在温度区间内的分布情况,以温度队列为基础,提出了一种基于负荷温度的密度聚类集群控制策略。
以上研究多数集中在对直热式电采暖等温控负荷进行需求响应管理,缺乏对蓄热式电采暖等储能负荷响应优化控制策略的研究。本文旨在通过响应优化进一步研究蓄热式电采暖与配电网之间的互动模式。在考虑用户供暖需求差异特征和蓄热式电采暖设备运行模式的情况下,提高蓄热式电采暖与配电网之间的匹配性,充分发挥蓄热式电采暖在缩小电网峰谷差,优化配电网负荷曲线等方面的能力。
1 负荷模型
1.1 用户热负荷需求计算模型
用户热负荷需求计算模型主要参考房屋热力学模型。采集用户房屋实际供暖面积S(i)、体积Vm,i、用户每时段的室内温度Tin、台区每时段的室外平均温度Tout等相关参数,计算用户各时段热负荷需求表达式为
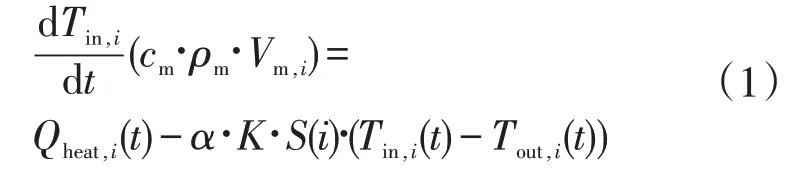
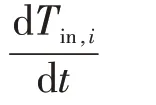
1.2 蓄热式电采暖负荷计算模型
采集台区用户蓄热式电采暖设备运行额定输入功率P、设备制热效率η等相关参数,忽略设备储热材料的自身变化。其中,单体蓄热式电采暖负荷表达式如式(2)所示,不同启停状态下单体蓄热式电采暖模型蓄放热表达式如式(3)和式(4)所示

若Wi(t)=1,IC,i(t)=1且ID,i(t)=0,则
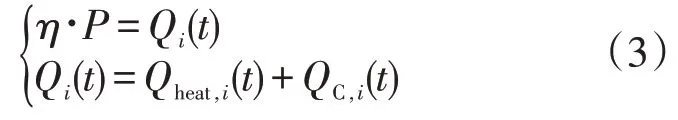
若Wi(t)=0,IC,i(t)=0且ID,i(t)=1,则

式中:P i(t)为用户t时段蓄热电采暖耗电功率,kW;Wi(t)为t时段蓄热电采暖的启停状态,1为开启,0为关闭;IC,i和ID,i分别为t时段储热罐蓄热和放热状态;η为设备制热效率;P为蓄热电采暖输入额定功率,kW;Qi(t)为t时段蓄热电采暖制热功率,kW;Qheat,i(t)为t时段蓄热电采暖设备供热功率,kW;QC,i(t)和QD,i(t)分别为t时段蓄热功率和放热功率,kW。
蓄热罐初始蓄热量与用户使用情况有关,需另外监测或计算。用户每时段储热罐蓄热量表达式如式(5)所示
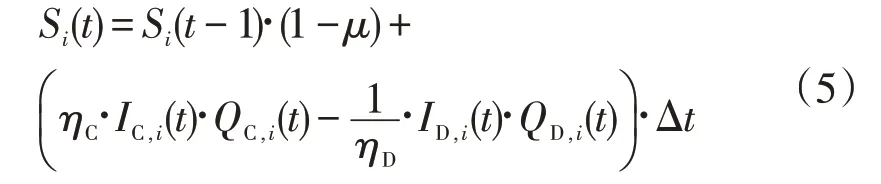
式中:S i(t)为t时段蓄热式电采暖储热罐蓄热量,kWh;μ为储热罐自身向环境散热造成的损失;ηC和ηD分别为储热罐蓄热和放热效率;Δt为单位时段。
2 匹配策略
本文提出的配电网与蓄热式电采暖负荷的优化匹配策略具体步骤如下,流程图如图1所示。
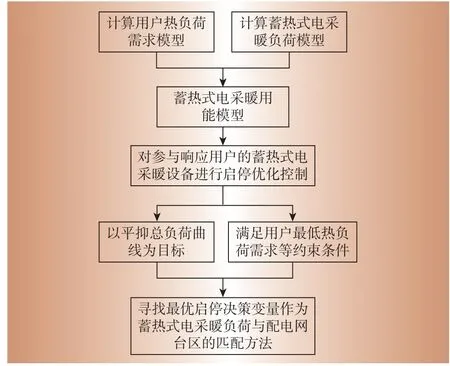
图1 匹配方法流程图Fig.1 Flow chart of matching method
(1)结合用户热负荷需求计算模型,计算用户各时段热负荷需求。
(2)结合蓄热式电采暖负荷计算模型,采集参与响应用户可控时段(谷时段),对其各时段蓄热式电采暖设备进行DLC,不可控时段(峰时段)内设备断电放热。根据峰谷分时电价,20:00至次日8:00为谷价时期,用户用电行为较少,配电网台区其他负荷较低。为配合错峰用电,更好地发挥削峰填谷作用,设定台区用户在谷期20:00至次日8:00才会对蓄热设备通电,同时这段时间为可控时段。
(3)将所有用户的蓄热式电采暖设备接入配电网台区,以平抑台区总负荷曲线、减小峰谷差为目标得到蓄热式电采暖负荷响应优化模型。
(4)根据随机的启停策略计算各时段储热罐蓄热量,考虑储热罐容量限制、用户最低热负荷需求等约束,筛选用户设备可能的启停策略。在筛选出的启停策略中寻找最优决策变量,作为蓄热式电采暖负荷与配电网台区的匹配方案。
2.1 蓄热式电采暖负荷响应优化模型建立
2.1.1 目标函数
假设台区有N个用户,所有用户全部参与响应,用户在能满足自身热负荷需求的情况下只采用蓄热式电采暖设备供暖,那么优化后t时段该台区蓄热式电采暖负荷PX(t)为
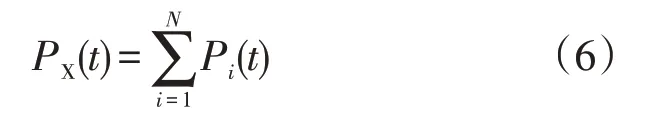
已知t时段配电网台区其他负荷为PQ(t),那么接入优化控制的蓄热式电采暖后,t时段配电网台区总负荷PZ(t)为

以平抑配电网台区总负荷曲线,减小峰谷差为目标,用曲线的方差来衡量曲线平坦程度,得到目标函数
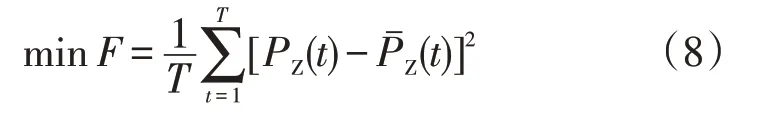
2.1.2 约束条件
(1)为保证稳定运行,各时段蓄热式电采暖储热罐蓄热量需满足
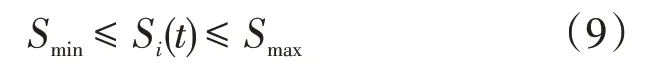
式中:Smin和Smax分别为储热罐最小和最大蓄热量,kWh。
(2)储热罐蓄放热功率约束
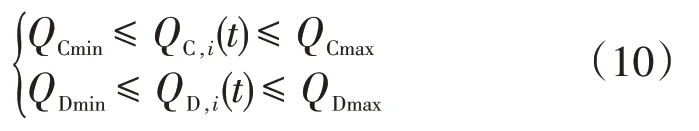
式中:QCmin和QCmax分别为储热罐最小和最大蓄热功率,kW;QDmin和QDmax分别为储热罐最小和最大放热功率,kW。
(3)蓄热式电采暖供热量需满足用户全天最低热负荷需求,即
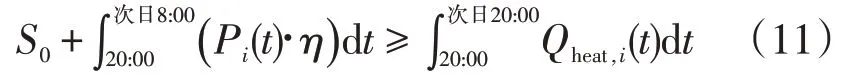
式中:S0为储热罐初始蓄热量,kWh。
2.2 蓄热式电采暖负荷响应优化模型求解
本文采用遗传算法进行模型求解,利用轮盘赌和精英保留的方式[6—7],选择较为优秀的父代产生子代并将每一代的优越个体保留到下一代,同时产生的子代数量会补齐种群数量的空缺。本文将蓄热式电采暖负荷响应优化模型中的目标函数作为遗传算法中的适应度函数。在可控时段内,以每30 min为一时段,对第i个用户t时段蓄热式电采暖设备的启停状态Wi(t)(取值为0或1)进行编码,作为遗传算法的求解对象。
3 算例分析
以某一台区的冬季典型日作为算例,该台区共有30个用户。根据用户家庭人口数量不同,取实际供暖面积范围为60~90 m2。根据《关于完善北京市城镇居民“煤改电”居民采暖季电价优惠政策的意见》(京环函[2019]209号)内容,规定“煤改电”分散采暖居民补贴后谷段电价为0.100 0元/kWh、峰段电价为0.488 3元/kWh、谷电时段为20:00至次日8:00。统一选择额定输入功率P=3.2 kW的蓄热电暖器,其他参数:η=0.85,μ=0,ηC=ηD=1,Smin=0,Smax=16.8 kWh,QCmin=QDmin=0,QCmax=QDmax=3.2 kW,储热罐初始蓄热量取S0=0.5 kWh。
实际情况下用户一般会在连续时段通电蓄热。基于峰谷分时电价,考虑用户用电成本,假设该台区用户在20:00至24:00自行开启蓄热电暖器,直至次日日间峰值电价时段(8:00之后),或储热罐蓄热量达到最大容量时才断电关闭。
采用前述优化匹配策略对配电网台区蓄热式电采暖负荷进行优化。根据相关标准规范,人体舒适温度范围为18~23℃。优化过程中热负荷需求取用户能接受的最低值,即用户室内温度维持在18℃。在可控时段内,对用户蓄热式电采暖设备进行DLC。结合前述蓄热式电采暖负荷响应优化模型,采用遗传算法求解,种群数取100个,迭代次数取100次,得到台区用户的DLC优化决策结果。
根据求解得到的优化后配电网台区用户蓄热式电采暖设备启停策略,可叠加得到优化后配电网台区蓄热式电采暖负荷,与实际配电网台区蓄热式电采暖负荷对比如图2所示,优化后配电网台区蓄热量随时间变化曲线如图3所示。
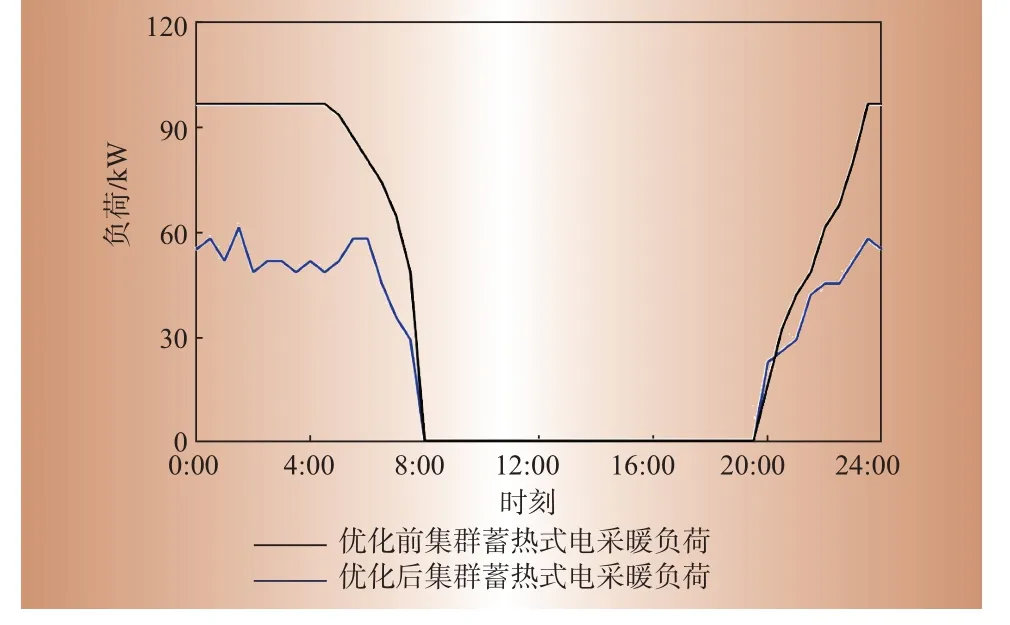
图2 优化前后配电网台区蓄热式电采暖负荷对比Fig.2 Load comparison of regenerative electric heating in distribution network area before and after optimization
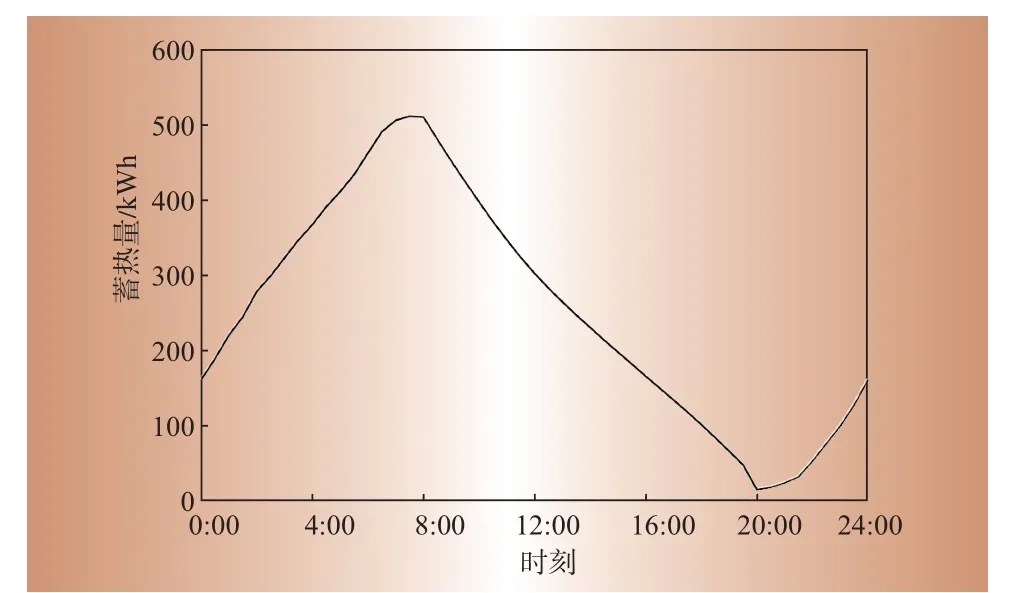
图3 优化后配电网台区蓄热式电采暖蓄热量随时间变化关系Fig.3 The relationship between stored heat of regenerative electric heating in distribution network and time after optimization
结合图2、图3可知,在满足用户舒适度要求的情况下,优化后配电网台区蓄热式电采暖夜间高峰负荷由96 kW削减至60 kW左右,但负荷曲线趋势仍和优化前相近,呈现中间低两边高的形态。由此可知,响应策略实施效果较明显,在满足用户最低热负荷需求的同时削弱了由于供暖集中带来的新负荷高峰,优化后蓄热式电采暖负荷仍保留了时移性特征。
3.1 直热式电采暖与优化后蓄热式电采暖对配电网台区总负荷的影响
在用户响应概率分别为30%、60%、90%和100%的场景下,对比接入优化蓄热式电采暖与全接入直热式电采暖的台区总负荷曲线,如图4所示(蓝色曲线为优化后配电网台区总负荷,黑色曲线为全接入直热电采暖时配电网台区总负荷)。同时计算相应总负荷特性指标如表1所示。
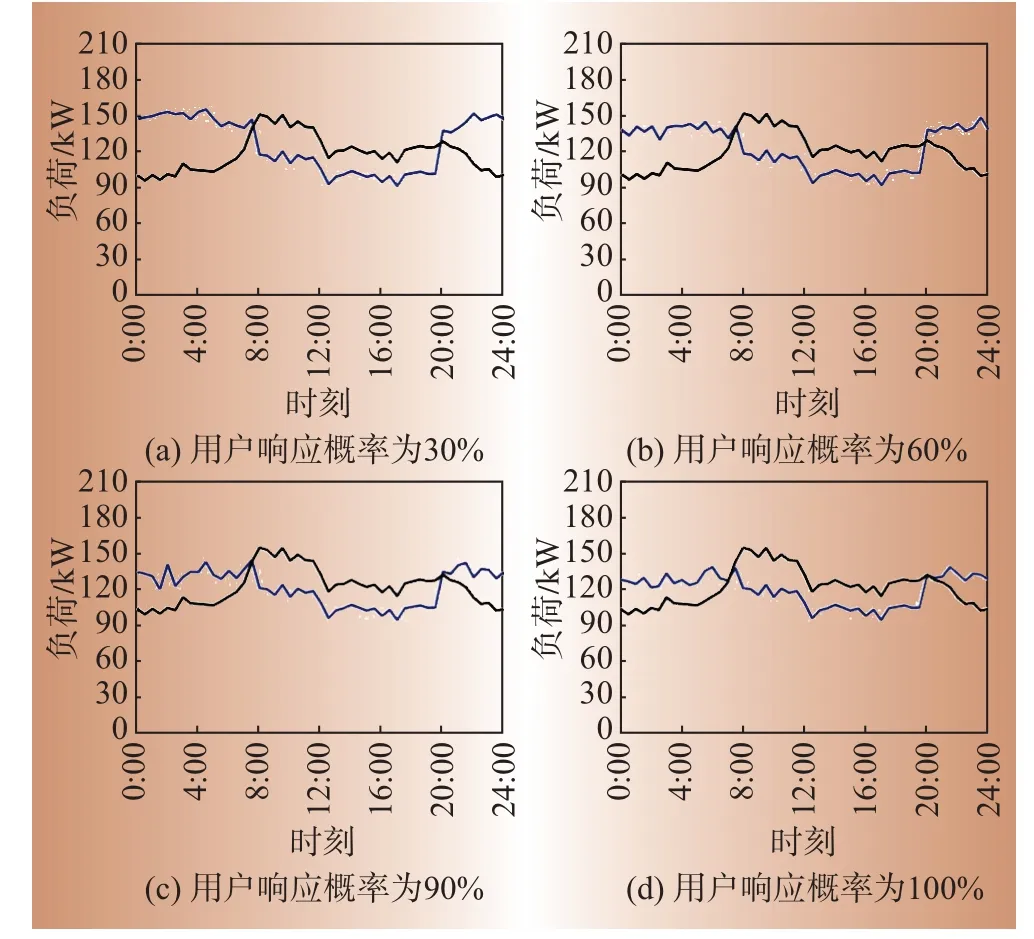
图4 多场景下接入优化蓄热式电采暖对配电网台区负荷的影响Fig.4 Influence of optimized regenerative electric heating on distribution network load in multi-scenarios
由图4可见,随着用户响应概率的提高,原本由于蓄热电采暖设备使用过于集中带来的夜间新负荷高峰得到削减,总负荷曲线趋于平缓。如表1所示,当用户响应概率从30%增加到60%时,负荷峰谷差率和波动率减小。虽然此时优化后蓄热式电采暖对台区总负荷起到削峰填谷作用,但供暖集中产生的新负荷高峰仍然存在,蓄热式电采暖的优势不明显。当用户响应概率继续提高时,优化后台区总负荷峰谷差率、波动率均小于全接入直热式电采暖的台区总负荷,蓄热式电采暖与台区匹配特性增强,实现了蓄热式电采暖与配电网台区互动模式优化。

表1 多场景下接入优化蓄热式电采暖后配电网台区总负荷特性指标Table 1 Total load characteristic indexes of distribution network station area after connecting optimized regenerative electric heating in multi-scenarios
3.2 蓄热式电采暖优化前后对配电网台区总负荷的影响
同样在用户响应概率分别为30%、60%、90%和100%的场景下,分析优化前后配电网台区总负荷变化。不同用户响应概率下,响应能力即为挖掘的蓄热式电采暖负荷与配电网台区互补潜力,如图5阴影部分所示(蓝色曲线为优化后理想配电网台区总负荷,黑色曲线为优化前实际配电网台区总负荷)。同时计算相应总负荷特性指标如表2所示。
如图5所示,随着用户响应概率的提高,阴影部分面积逐渐增大,用户响应容量的叠加体现了蓄热式电采暖负荷与配电网台区的交互潜力。如表2所示,随着用户响应概率的提高,优化后配电网台区总负荷峰谷差率和波动率逐渐减小,且均小于优化前。定量分析不同场景下响应能力,表明了全响应时潜力最大,匹配度最高,为最优匹配。
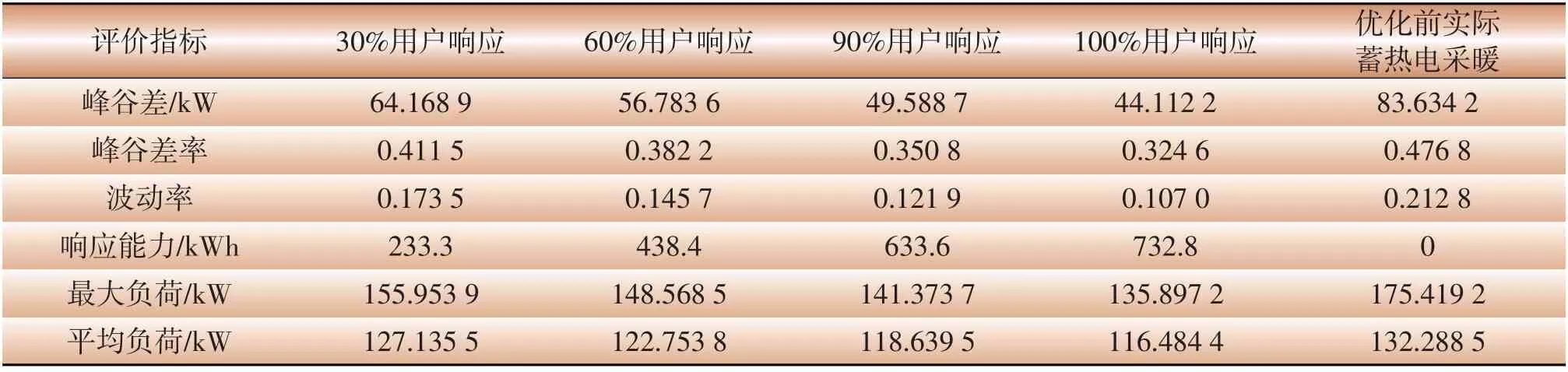
表2 多场景下优化前后配电网台区总负荷特性指标Table 2 Total load characteristic indexes of distribution network station area before and after optimization in multi-scenarios
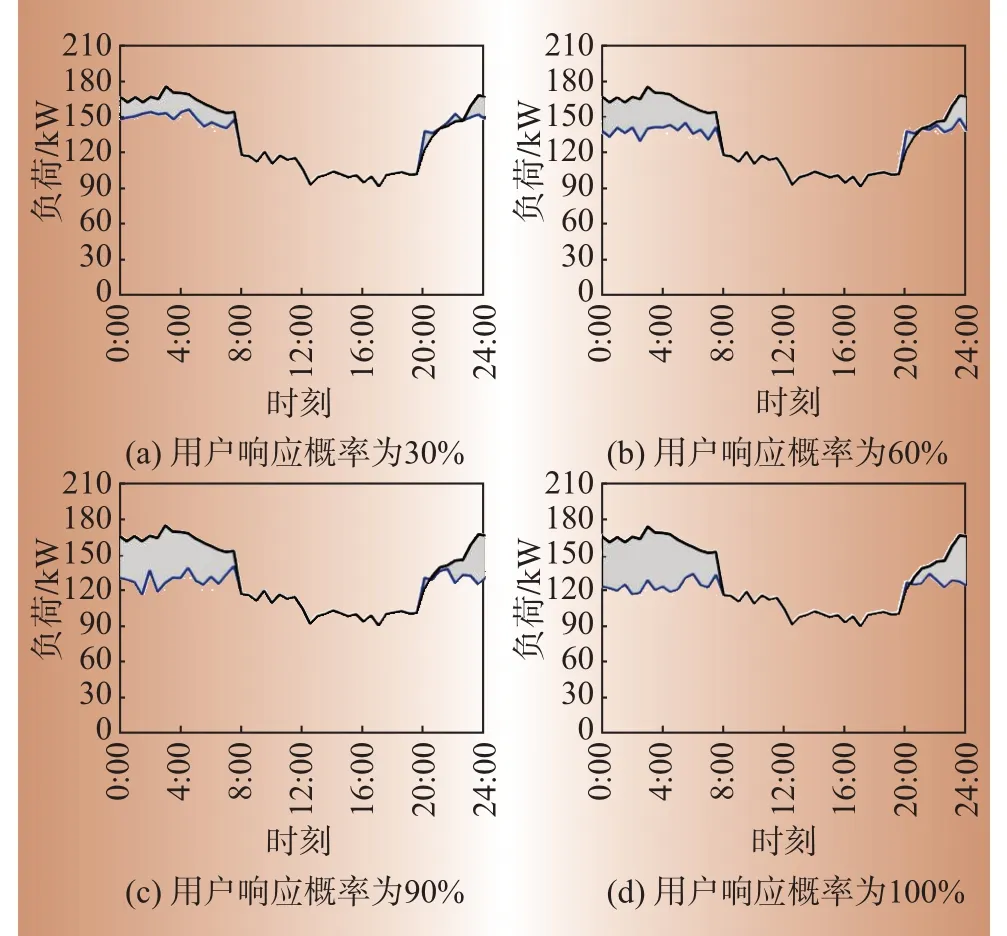
图5 多场景下优化前后配电网台区总负荷变化Fig.5 Changes of total load in distribution network area before and after optimization in multi-scenarios
4 结束语
本文在研究蓄热式电采暖与配电网交互方式时,考虑设备储热罐容量限制、用户热负荷需求等约束,采用需求响应中的DLC策略,以匹配配电网台区负荷为目标,建立蓄热式电采暖负荷响应优化模型,优化参与响应用户的蓄热式电采暖负荷,减小了采暖过于集中带来的新负荷高峰,充分发挥了蓄热式电采暖减小电网峰谷差的优势。既符合实际使用情况又满足用户舒适度要求,利于充分发挥蓄热式电采暖的优势,对其大规模推广具有一定意义。D
