Mn对中锰钢α-Fe／γ-Fe界面影响的第一性原理研究

陈万超 汪 杨 杨 晴 张恒华 张 梅

（上海大学材料科学与工程学院，上海 200444）

随着我国人民生活水平的大幅度提高，私家车的保有量不断增长，由此衍生的环境、能源和安全三大问题成为开发汽车用先进高强度钢的主要推手。中锰TRIP钢是一种具有高强塑性的高强钢，其减重效果虽然不及铝合金和镁合金等，但是卓越的强塑性使它在汽车制造业始终占据一席之地［1-3］。

中锰TRIP钢的原始组织为马氏体，经过奥氏体逆相变退火并冷却至室温得到铁素体和残留奥氏体双相组织。在逆相变退火过程中，部分马氏体转变成奥氏体，剩余的马氏体由于碳元素的扩散使其碳含量不再饱和而转变成铁素体，随后发生的锰元素配分起到稳定奥氏体和细化铁素体晶粒的作用［4］；该过程中也有碳化物的形核析出，起沉淀强化作用，前人对其已有充分的研究。Jung等［5］采用第一性原理计算了FCC-Fe／MCs（NaCl结构，M＝Ti，Zr，Hf，V，Nb，Ta）体系的共格界面能和半共格界面能，得出FCC-Fe／MCs体系的共格界面能低于BCC-Fe／MCs体系，BCC-Fe／MC体系的半共格和共格界面能随失配量的增加而增大，奥氏体钢中VC的沉淀强化效果最好。熊辉辉［6］采用第一性原理计算研究了铁原子在（A1-xMx）C（A＝Nb，Ti；M＝Mo，V）复合碳化物以及A（C1－xNx）（A＝Nb，Ti）复合碳氮化物的（001）表面的吸附行为，发现TiC（或NbC）晶格中的Ti（Nb）被Mn、V取代后形成的复合碳化物均有利于形核，Fe在（Nb0.5Mo0.5）C（001）表面具有最大吸附能和最短Fe—C键长。

Mn是中锰钢的主要合金元素［4］，锰的加入会促进逆相变退火过程中奥氏体的形核，导致室温下残留奥氏体量增加。在奥氏体逆相变过程中，奥氏体在马氏体板条间长大，同时碳和锰在两相间配分［7］。为了研究该过程中Mn配分对两相区奥氏体的体积分数和稳定性的影响，本文建立了铁素体／奥氏体（α-Fe／γ-Fe）两相界面，采用第一性原理计算方法分析了α-Fe／γ-Fe界面稳定性和界面电子结构。

1 计算方法与模型建立

1.1 计算方法

本文计算均采用基于密度泛函理论［8］（density functional theory，DFT）结合平面波赝势方法的CASTEP（Cambridge sequential total energy package）软件包，使用超软赝势描述原子核与电子之间的相互作用。为了得到合适的截断能（Ecut）和k点，对α-Fe（体心立方，空间群IM-3M）与γ-Fe（面心立方，FM-3M）的结构进行了单点能收敛测试；为了得到合适的电子交换-相关泛函，选取3种电子交换关联泛函（GGA-PBE，GGA-PW91，LDA-CAPZ）对α-Fe和γ-Fe的结构进行优化计算，其晶胞参数的计算结果如表1所示。

对比表1的计算结果，本文计算采用的电子交换-相关泛函为GGA-PBE，所有计算在倒易空间上进行，第一布里渊区积分采用Monkhorst-Pack方案形成的特殊k点方法。对于体相α-Fe与γ-Fe，k点网格划分为9×9×9；对于所有表面和界面模型，k点划分均为9×9×1。最大平面波截断能为400 eV，采用Broyden-Fletcher-Goldfarb-Shanno（BFGS）算法进行几何优化，实现原子的充分弛豫。收敛条件是自洽计算最终两个循环能量之差小于1×10－5eV／atom，作用在每个原子上的力不大于0.03 eV／Å，内应力不大于0.05 GPa。

表1 α-Fe与γ-Fe点阵常数的计算值与试验值Table 1 Calculated and experimental values of lattice constants of α-Fe and γ-FeÅ

1.2 表面模型优化

铁素体与奥氏体满足K-S取向关系：α-Fe（110）／γ-Fe（111）［15］。为了确定奥氏体和铁素体表面的最小原子层数，保证构建界面的两侧Fe原子表面深处呈现体相原子的特征，对α-Fe（110）和γ-Fe（111）表面模型进行收敛性测试。这两个表面模型均为非极性的特征，因此可根据表面能随原子层数的变化来确定所需原子层数，其表面能［16］可根据式（1）计算得出：

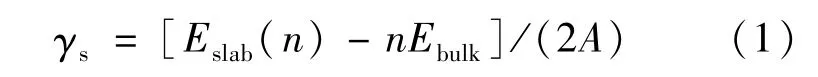
式中：Eslab（n）和Ebulk分别表示该相表面结构的总能量和组成表面结构单个原子（或分子）的能量；n表示原子（或分子）的个数。表面能的计算结果如表2所示。

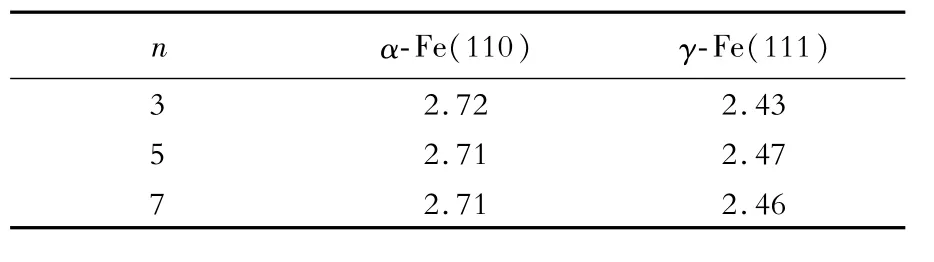
表2 α-Fe（110）和γ-Fe（111）的表面能收敛趋势Table 2 Convergence trend of surface energy of α-Fe（110）and γ-Fe（111）J／m2

从表2可以看出，当n≥5时，α-Fe（110）和γ-Fe（111）表面能（γs）分别收敛于2.71和2.46 J／m2。为了计算方便，选择5层原子层厚度的α-Fe和γ-Fe构建界面。

1.3 α-Fe／γ-Fe界面模型优化

根据α-Fe／γ-Fe的取向关系建立的界面模型如图1所示，共20个Fe（10个α-Fe原子，10个γ-Fe原子），将5层γ-Fe（111）堆垛在5层α-Fe（110）表面上，并在上下表面分别添加15 Å的真空层以消除两者之间的相互作用。经过晶胞优化后，用Mn原子分别置换界面次近邻层的α-Fe原子（Case 1）、最近邻层的α-Fe原子（Case 2）和γ-Fe原子（Case 3）以及次近邻层的γ-Fe原子（Case 4），此时界面系统Mn的质量分数约为5%；未进行Mn原子置换的界面记为Clean。

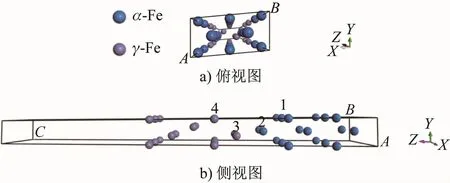
图1 未驰豫的α-Fe／γ-Fe界面模型Fig.1 Model of the unrelaxed interface of α-Fe／γ-Fe

分离功［8］（Wsep）在界面系统中定义为分离两凝聚相形成各自表面所作的可逆功，计算公式为：

式中：Eα、Eγ分别表示弛豫的游离α-Fe和γ-Fe表面结构的总能量；Eα／γ表示该界面的总能量；A表示界面面积。在热力学上，分离功越大，界面越稳定。

两固相的界面能［16］（γint）计算公式为：

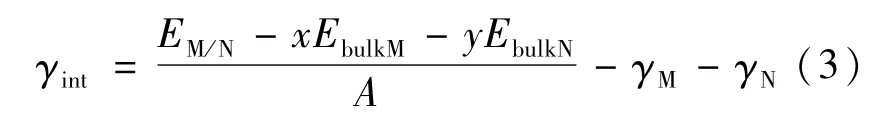
式中：EbulkM和EbulkN分别表示M（α-Fe）相和N（γ-Fe）相中单个原子（或分子）的能量，x和y是界面模型中两相原子（或分子）的个数；γM与γN表示两相的表面能；A表示界面面积。固相间的界面能定义为形成单位面积的界面时所增加的吉布斯自由能，但其本质上源于界面处的原子晶格畸变、化学键的改变和结构应变［7］。如果两个不同的固相之间能够形成一个稳定的界面，则该界面的界面能应为正值，且界面能越小，在热力学上越稳定。

在经典形核理论中，晶界形核所需的临界形核功G*和临界形核半径r*分别如式（4）和式（5）所示，可以看出，界面能越小，临界形核半径和临界形核功越小，越有利于形核［14］。

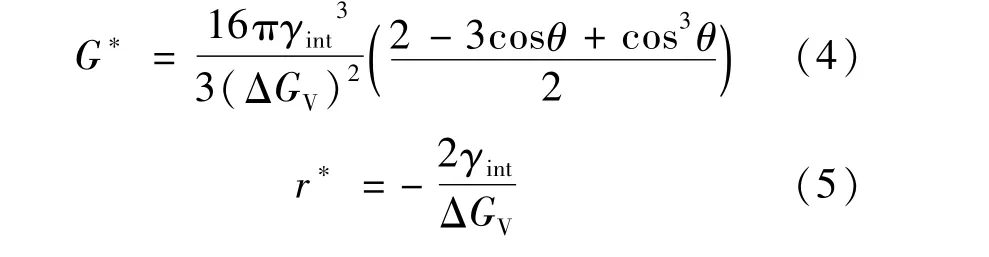
式中：γint为铁素体与奥氏体之间的界面能；θ为晶核γ-Fe和α-Fe的接触角；GV为体系的体积自由能。

2 计算结果与讨论

2.1 Mn对界面稳定性的影响

Mn原子置换前后界面系统的界面能和分离功如图2和表3所示。可以看出，Mn原子的置换对界面性质有一定影响。当Mn的质量分数上升至5%时，界面系统的分离功（Wsep）从负值变为正值（Case 1除外），界面稳定性提高，奥氏体形核位点增加，其中置换界面次近邻γ-Fe原子（Case 4）的分离功最大。置换界面最近邻层的α-Fe原子（Case 2）、γ-Fe原子（Case 3）和次近邻的γ-Fe原子（Case 4）的界面能（γint）相比Clean界面能均下降，界面更稳定，与分离功变化趋势一致。

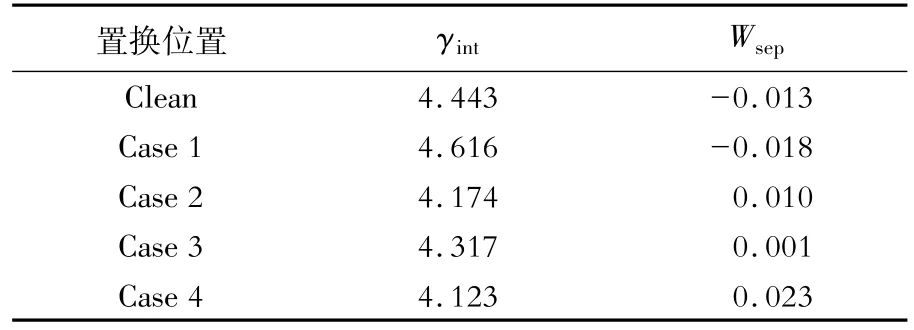
表3 Mn原子置换Fe原子前后界面系统的分离功和界面能Table 3 Separation work and interface energy of interface system before and after replacing Fe atom by Mn atomJ／m2

图2 Mn原子置换Fe原子前后的界面系统的分离功和界面能变化Fig.2 Variation of separation work and interface energy of interface system before and after replacing Fe atom by Mn atom

界面能源于晶格畸变和化学键，而晶格畸变直接导致界面两端铁素体与奥氏体的晶格错配度μ的变化，晶格错配度的计算公式［17］如式（6）所示，根据式（6）计算的错配度如表4所示。

表4 Mn原子置换Fe原子后界面系统的晶格错配度Table 4 Lattice mismatch degree of interface system after replacing Fe atom by Mn atom%

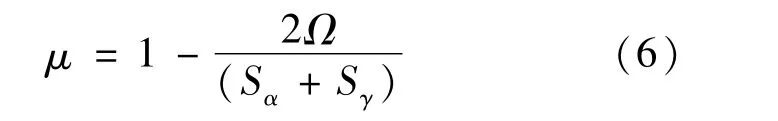
式中：Ω为α-Fe相表面和γ-Fe相表面封端重叠部分的面积；Sα和Sγ分别为界面两端α-Fe和γ-Fe相表面封端的面积。

结合晶格错配度，从热力学角度解释界面能的变化原因：α-Fe和γ-Fe形成界面两相引起晶格畸变，导致晶格错配度发生变化。但本文讨论的是Mn原子进入界面产生的晶格畸变，因此把Clean的晶格错配度定义为零；Case 1相比Clean界面能上升的原因可能是Mn原子进入奥氏体使得α-Fe和γ-Fe晶格错配度从0提高到0.322%；Case 2、Case 3及Case 4的晶格错配度分别为0.642%、1.295%、0.314%，但相比Clean界面能都下降，这可能是化学键变化所致。

从经典形核理论分析界面能的变化，Case 2、Case 3、Case 4的界面能相比Clean下降，说明这3种情况下奥氏体的形核功和形核半径减小，奥氏体形核数量增加且形核尺寸更小。其中Case 4的奥氏体形核数量最多且最细小，奥氏体热稳定性最好。

2.2 Mn原子对界面键合的影响

Milliken布居分析可以半定量地描述电荷转移量，用来判断键能的变化［6］。图3为Mn原子引入前后界面系统中各个原子的转移电荷数量。可以看出，Mn原子无论置换哪个位置的Fe原子，置换后的Mn原子相较于原来的Fe原子转移电荷数大量增加，Case 1～4中Mn的转移电荷数分别为0.20、0.18、0.18和0.17，所以Mn原子会形成一个强烈的正电场，吸引附近其他Fe原子周围的电子，形成共价键。在Clean中，界面最近邻层的5号和15号α-Fe原子（界面最近邻层的α-Fe原子）以及6号和16号γ-Fe原子（界面最近邻层的γ-Fe原子）转移电荷量都为0，表示此时界面两侧Fe原子相互作用较弱，界面键合较弱，保持亚稳状态（与负的分离功对应）；Case 1中，当Mn原子置换14号α-Fe原子后，5号和15号α-Fe原子转移电荷数变为－0.04、－0.02，而6号和16号γ-Fe原子转移电荷量仍为0，因此前者周围的负电荷被Mn原子吸引，远离了6号和16号γ-Fe原子，使得亚稳态的界面变得更不稳定，此时共价键作用与晶格畸变作用一致，使界面趋于不稳定，因此在共价键与晶格畸变双重作用下，界面能达到最高值；Case 2中Mn原子取代15号α-Fe原子后，6号和16号γ-Fe原子的转移电荷数变为－0.01和－0.06，被Mn原子产生的正电场所吸引，界面趋于稳定，共价键作用与晶格畸变作用相悖且占据主导地位，即使晶格畸变相比Case 1进一步加剧，但界面能仍然下降；Case 3中Mn原子取代16号γ-Fe原子后，5号和15号γ-Fe原子的转移电荷数变为－0.02和－0.03，并被Mn原子吸引形成共价键使界面结合更稳定，但此时共价键的作用比晶格畸变作用弱（Case 3相比Case 2的晶格畸变程度几乎翻倍，如表4所示），晶格畸变占据主导地位，导致界面能上升；Case 4中Mn原子置换17号γ-Fe原子，5号α-Fe原子转移电荷数变为－0.01，6号和16号γ-Fe原子的转移电荷数变为－0.01和－0.04，此时界面两侧Fe原子周围负电荷相互排斥使得界面变得不稳定，但Case 4相比Case 3的晶格畸变程度大幅度减小，界面能又下降。

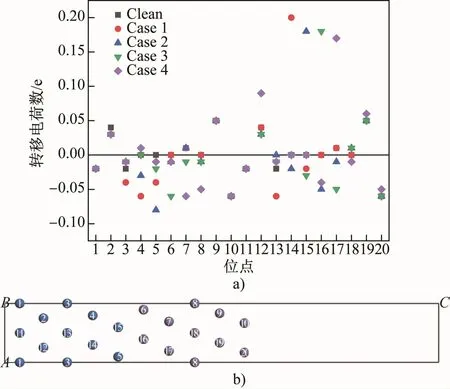
图3 锰的质量分数为5%的界面系统中各个位点原子的转移电荷数散点图（a）及位点编号（b）Fig.3 Scatter diagram of the number of transfer charges of atoms at each site（a）and site number（b）in the interface system with 5% Mn by mass

为了进一步阐述界面的电子性质，计算了Mn原子引入前后界面系统的总态密度（TDOS，total density of states），如图4所示。可见5种界面的总态密度曲线变化趋势相似，说明Mn原子置换对界面能的影响不大。费米能级处的态密度可以反映界面的稳定性［17］，态密度越小说明界面越稳定，且态密度不为零证明界面存在金属键。从图4可知，费米能级处的态密度大小顺序为Case 4＜Case 2＜Case 3＜Clean＜Case 1，与界面能结果一致。此外，α-Fe（110）／γ-Fe（111）界面最显著的特征是费米能级两侧的峰1和峰2之间的态密度不为零，这是一个赝隙［18］。这个宽的赝隙（－1.5～2 eV）表明在α-Fe（110）／γ-Fe（111）界面还存在强定向共价键，因此这个界面同时存在金属键和共价键。

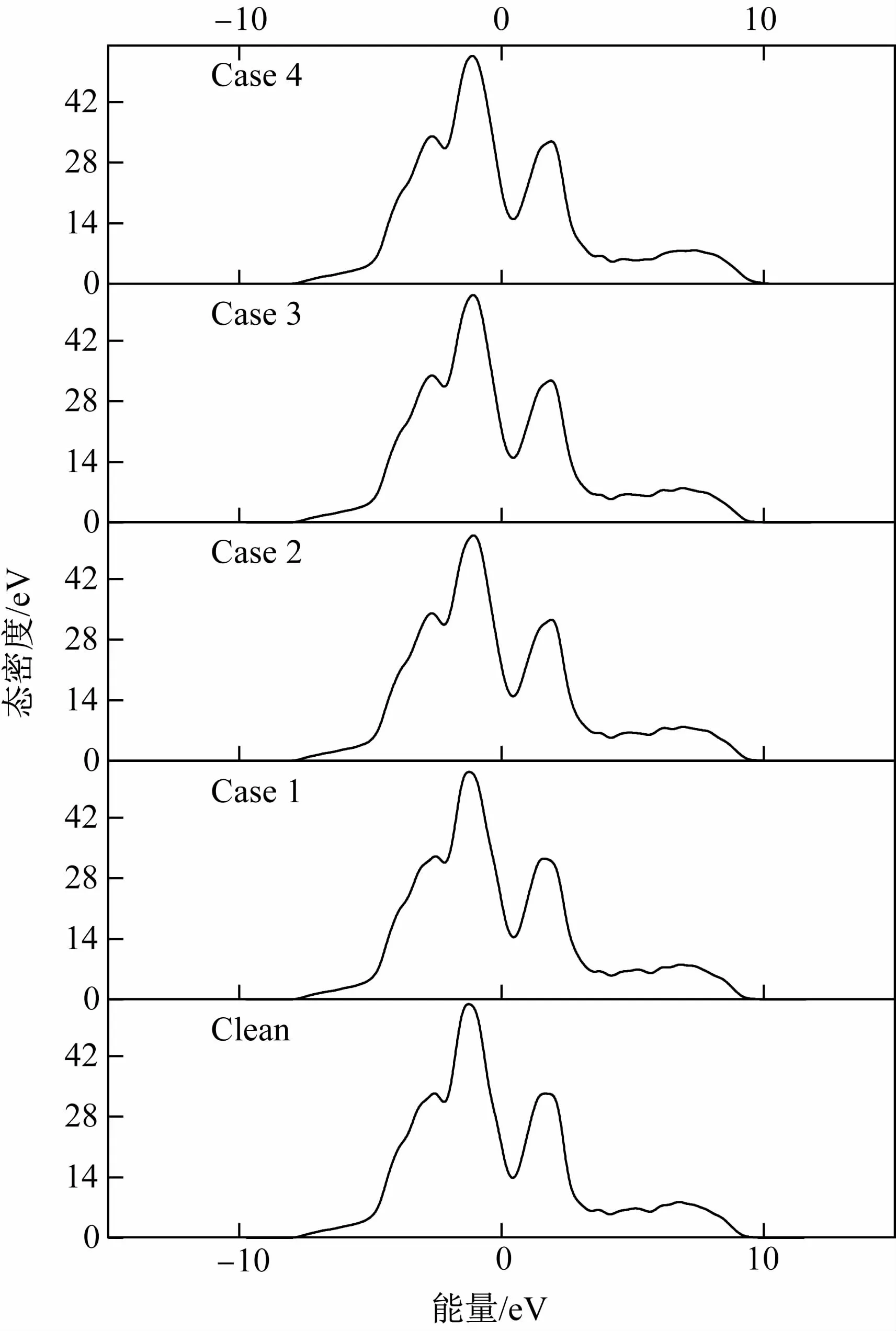
图4 5种界面系统的总态密度Fig.4 Total density of states of five interface systems

3 结论

（1）γ-Fe（111）表面和α-Fe（110）表面均于5层达到收敛，表现出明显的体相特征。

（2）Mn原子置换Fe原子后，一方面使界面两侧铁素体和奥氏体之间的错配度发生不同程度的变化，即界面的晶格畸变程度发生变化；另一方面使各个原子的转移电荷数发生变化，即界面共价键和金属键强度发生变化。晶格畸变程度和化学键强度变化共同作用使界面能发生变化。

（3）Mn的质量分数为5%时，Mn向奥氏体一侧扩散使得α-Fe／γ-Fe界面更加稳定，同时由于界面能的下降，奥氏体的临界形核功和形核尺寸减小，奥氏体的形核数量和热稳定性提高。