基于退役同步发电机组的无功补偿接入点研究

吕金历，孔 宁，白望望，冯智慧

（1.国网甘肃省电力公司经济技术研究院，兰州730050；2.兰州理工大学 电气工程与信息工程学院，兰州730050）

随着能源结构调整与可再生能源大规模发展，火电机组生存空间被持续压缩。如果退役同步发电机组直接淘汰，将面临资源大量浪费等问题。将退役同步发电机组改作调相机运行能够有效解决以上问题，可在保证退役同步发电机组二次利用的同时，为系统提供更高的无功支撑，维持系统转动惯量，提高系统稳定性。

同步发电机机组改作调相机运行时，运行地点保持原有厂址不变。因此，在其近区筛选合适的无功补偿接入点是一个亟待解决的实际问题，同时也是充分发挥其无功补偿作用的前提。结合同步调相机自身的运行特点，解决上述问题可参考无功补偿装置布点问题研究。关于布点问题的研究一般采用静态电压稳定分析方法，主要包括模态分析法[1]、U-Q 灵敏度法[2]、先导节点法[3]、向量场正规形理论[4]等。通过对系统进行静态电压稳定分析，辨识整个网络的薄弱区域与关键节点，从而确定无功补偿装置的最佳安装地点。在考虑暂态电压稳定情况下的无功补偿装置布点研究中，大多以维持故障情况下电压稳定为研究目标。文献[5]以故障后极限切除时间为指标，通过优化配置来确定无功补偿装置的安装地点。文献[6]以计及负荷特性的模裕度指标为基础，动态地搜索最佳无功补偿装置配置位置。部分文献以轨迹灵敏度（Trajectory Sensitivity Index，TSI）为基础，综合考虑无功补偿装置的实际特性、节点电压稳定的重要度和薄弱度，以确定最优布点方案[7-9]。以上研究均基于系统网络整体进行研究分析，整个过程较为复杂。

为简化无功补偿装置布点问题，部分研究通过对电力系统网络进行分区，将无功补偿装置布点问题转移到较小的分区内，以简化分析过程[10-11]。文献[12-13]以局部电压稳定指标为依据，对系统网络节点进行有效划分，并通过灵敏度计算来识别系统关键节点。

本文提出一种基于退役同步发电机组的动态无功补偿装置接入点筛选方法。以电力系统节点阻抗为依据，计算节点间电气距离，构成节点特征矩阵。对各节点特征进行层次聚类（Hierarchical Clustering）分析，实现节点自动分区。在确定退役同步发电机组所补偿分区后，计算其所在分区内节点重要度指标值，按重要度将其排序，筛选关键节点为无功补偿接入点。对IEEE-39 节点标准系统进行分析，验证本文所提方法的有效性及可行性。

1 负荷节点分区

1.1 节点电气距离

当电网内某个节点的变量发生变化时，其附近区域节点的运行状态也随之改变，这种关系称为节点间的耦合性。在电力系统中，通常采用“电气距离”来表示任意两节点之间的电气耦合程度，其值越小，耦合性越强。

文献[14]将电气距离定义为电网络中任意两节点间的等值阻抗Zij，equ。当任一节点i 注入单位电流元，节点i 与j 之间的等值阻抗Zij，equ在数值上等于电压Uij，如图1所示。

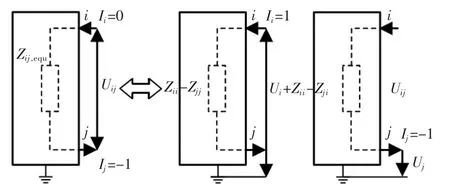
图1 电气距离计算原理图Fig.1 Principle diagram of electrical distance calculation

Zij，equ可采用系统节点阻抗矩阵元素表达，如式（1）所示：

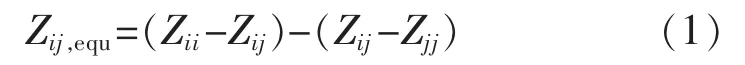
式中：i、j 分别表示等值阻抗的起始节点和终点节点；Zij为节点阻抗矩阵中元素。

1.2 基于聚类分析的负荷节点分区

传统的电力系统分区按照地域、所属公司或服务对象等进行划分，上下层级明确，便于整体规划管理。但这样的电网划分并未考虑系统运行时的电气特性。本文基于电气距离，应用层次聚类算法对其进行分析，实现电网节点的有效划分。

层次聚类是聚类算法的一种，通过对比数据点间的相似度程度，用一棵有层次的嵌套聚类树来表示聚类结果。在聚类树中，最底层为各个原始数据点，顶层是每一个聚类的根节点。聚类结果将数据集按照其内部特征分割成不同的类或簇，使得同一个簇内数据对象的耦合性尽可能大，不在同一簇内数据对象的耦合性尽可能小。

设X=｛x1，x2，…，xn｝为待分类的节点集合，节点特征由两节点间的电气距离来定义。则节点特征矩阵如式（2）所示：

式中：矩阵内元素为电力系统两节点间电气距离，Znm，equ可以理解为第n 个节点的第m 个特征，即系统中n 节点与m 节点间电气距离。本文将矩阵第n行定义为节点n 的特征集合，如式（3）所示：

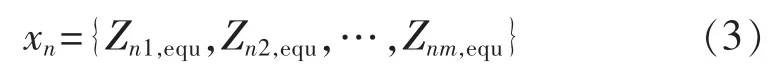
根据每个节点的m 个特征，将负荷节点无功电压分区转化为节点聚类问题。层次聚类法可以对n节点的m 个特征进行数值分析，使得簇内节点耦合性强，簇间节点耦合性弱，以达到节点分区的目的。

基于电气距离对电网络节点进行层次聚类，实现节点分区，可以简化退役同步发电机组无功补偿接入点筛选问题。在确定补偿分区后，仅需对分区内节点进行分析即可。

2 系统关键节点判定

2.1 局部电压稳定指标

1986年P.Kessel 与H.Glavitsch 基于简单两节点线路模型，首次提出局部电压稳定指标（L 指标），并将其推广到多节点电力系统[15]。电网络中两节点电路模型如图2所示。

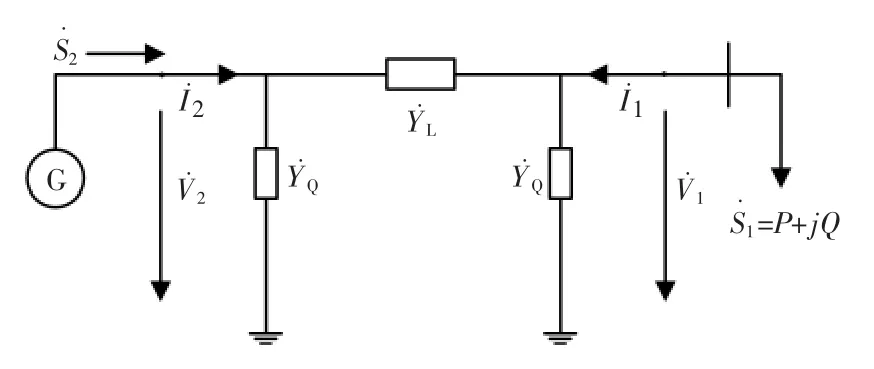
图2 两节点线路模型Fig.2 Two node line model

由系统导纳矩阵可知：

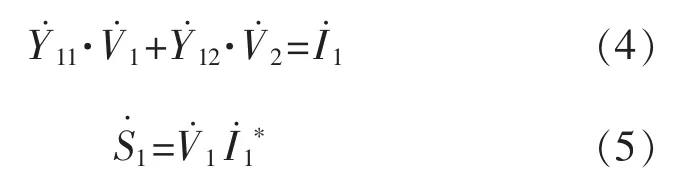
式（4）可转换为如下形式：

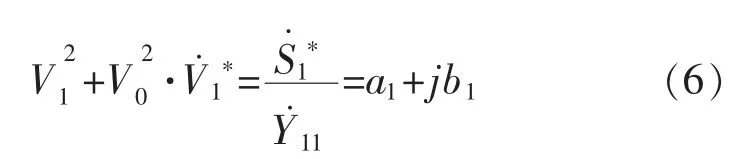
式中：* 表示共轭；a1，b1分别为实部和虚部；V0为等效电压，其表达式如式（7）所示：

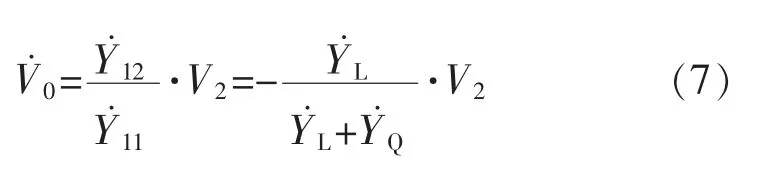
经过变换，可得两节点系统的稳定极限为

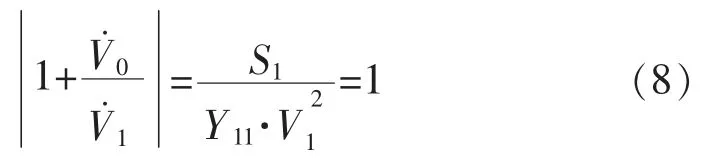
因此，可将电压稳定性评估指标用L 表示为

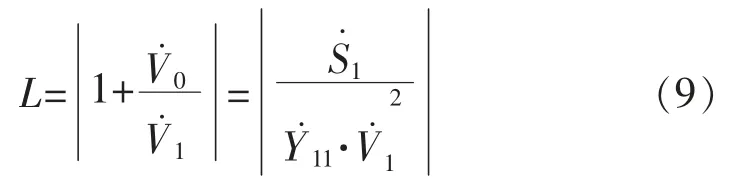
将L 指标拓展到多节点系统，且将网络中所有节点进行分类。一类为发电机节点集合αG，另一类为负荷节点集合αL。则负荷节点j 的电压稳定指标Lj可用式（10）表示：

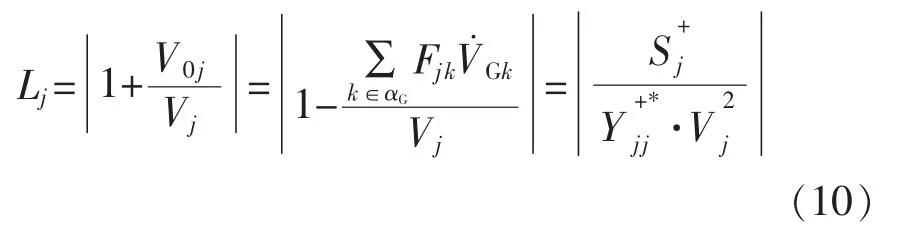
根据文献[16]，上述指标可转换为：

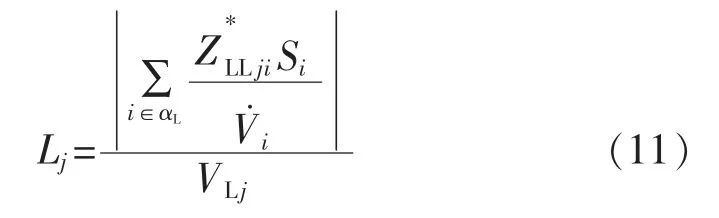
式中：ZLLji为负荷节点i 与j 之间的互阻抗；为负荷节点i 的电压相量；VLj为负荷节点j 的电压幅值；Si为节点i 的系统负荷功率。

局部电压稳定指标与系统节点电压稳定性的关系如下：

（1）L<1，节点电压稳定；

（2）L=1，节点电压临界稳定；

（3）L>1，节点电压失稳。

2.2 节点重要度指标

以电气距离为基础，定义系统中某一节点与其余节点间电气距离之和的倒数De，j为电气耦合度[14]：

De，j通过定量描述系统内任一节点j 与其余节点间的电气距离之和的大小，可以反映节点j 与其余节点间耦合关系强弱。De，j值越大，表明节点j 与系统其它节点之间耦合性越强，该点的运行状态变化对其它节点运行状态影响越大。即该节点发生暂态失稳时易引发连锁故障，是系统网络中的关键节点。

为了将不同节点的De，j指标差异度放大，同时更加准确地描述节点特性，故需对每个节点电气耦合度乘以适当的权重Wj。由于电压稳定性评估指标L 越大，节点稳定性越差，所以可以用L 表示节点电气耦合度的权重，即：

此处称Wj为负荷节点的稳定系数。当系统处于正常运行状态时，Wj取值范围为［0，1］。Wj值越大，表明节点稳定程度越低，发生外部扰动时越容易失稳，所处位置更为关键。

定义节点重要度指标为

Fj可以更加清晰地反映电网中某一节点的重要性，指导退役同步机组筛选合适的无功补偿接入点。

综上所述，退役同步发电机组改作同步调相机运行时，无功补偿接入点筛选流程如图3所示。

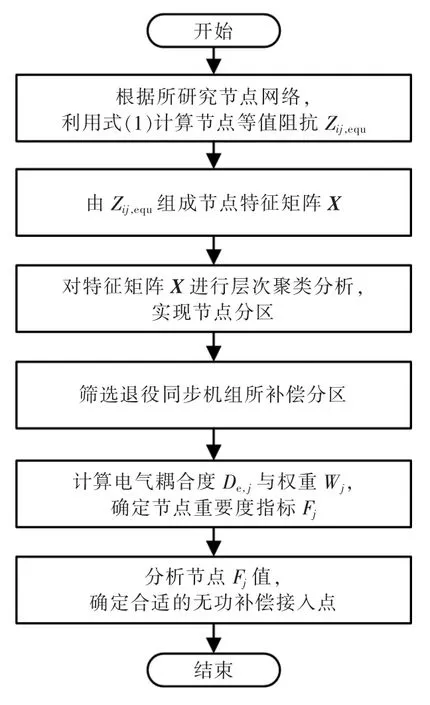
图3 无功补偿节点筛选流程Fig.3 Screening flow chart of reactive power compensation nodes

3 算例分析

以IEEE-39 节点标准系统网络为分析对象，验证所提方法的可行性，其拓扑结构如图4所示。

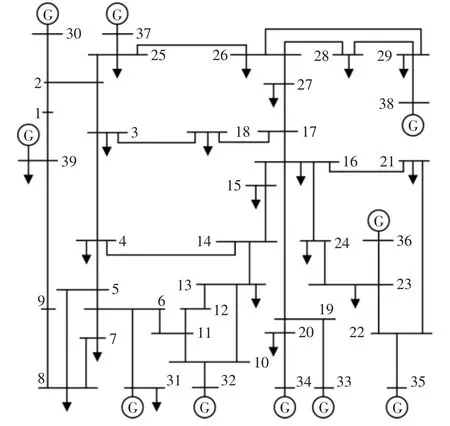
图4 IEEE-39 节点系统网络拓扑结构Fig.4 Network topology of IEEE-39 node system

图中节点1-29 为系统负荷节点，30-39 为系统发电机节点。在系统标准运行方式下，基于系统节点阻抗计算得到负荷节点电气距离如表1所示。

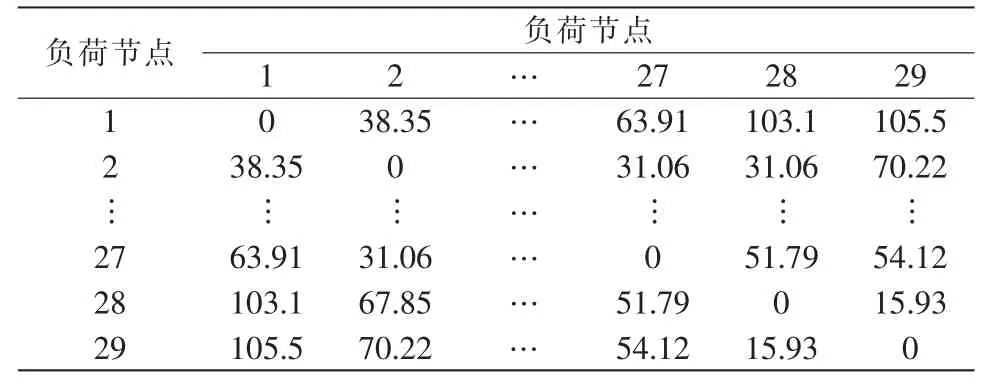
表1 负荷节点电气距离Tab.1 Electrical distance of load node

由表1可知，负荷节点间电气距离所组成特征矩阵为对称矩阵，且对角线元素为零，即节点与自身耦合性最强。电气距离用来反映节点间耦合关系的强弱程度，其值越大表明节点间耦合性越弱，越小表明节点间耦合性越强。

系统中任一节点与其余节点间电气距离构成该节点的特征元素，进而形成特征矩阵，对其进行层次聚类，结果如图5所示。

图5 IEEE-39 节点系统聚类过程Fig.5 Clustering process of IEEE-39 bus system

经层次聚类分析后，系统负荷节点分区结果如表2所示。

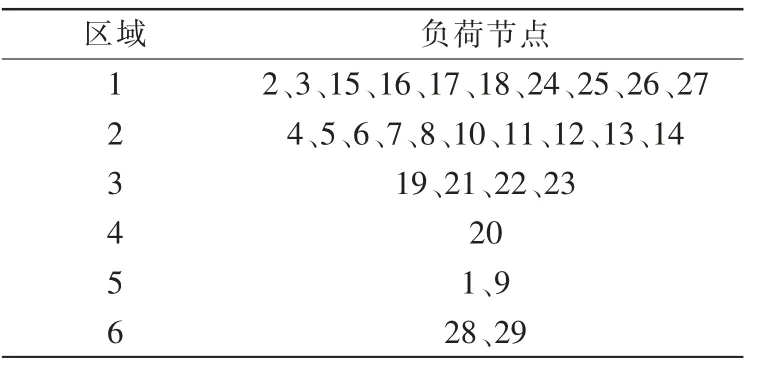
表2 负荷节点分区结果Tab.2 Load node partition results

以负荷节点间的等效电气距离为依据，进行层次聚类分析后得到6 个节点分区。其中节点20 为孤立节点，可将其按地理位置划入区域3。节点地理位置分布及分区如图6所示。

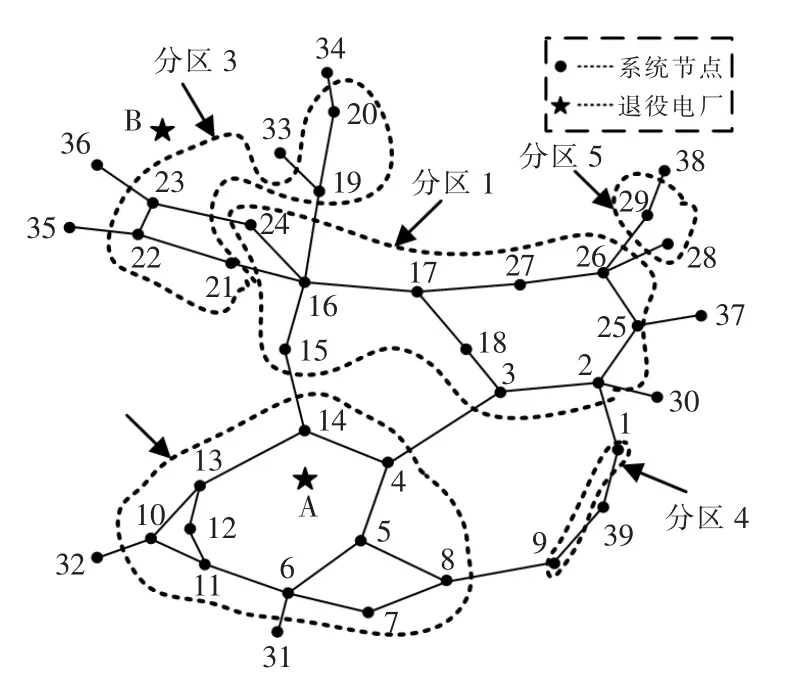
图6 负荷节点分区图Fig.6 Load node partition map

假设A、B 两处为已退役电厂，为避免直接淘汰造成资源浪费，同时提高区域电力系统稳定性，故将厂内同步发电机组改成同步调相机，作为系统的无功补偿装置。

A、B 两处厂址所处地理位置如图6标注所示。根据其所在地理位置，选择距离较近的节点分区为其无功补偿区域，即A 厂针对分区2 进行无功补偿，B 厂针对分区3 进行无功补偿。对分区2、分区3内节点进行筛选，确定合适的无功补偿接入点。

计算分区内节点重要度指标，如表3、表4所示。

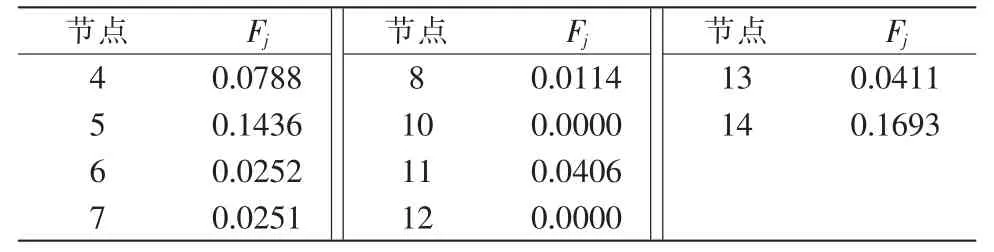
表3 分区2 节点重要度指标FjTab.3 Node importance index Fj in partition 2

表4 分区3 节点重要度指标FjTab.4 Node importance index Fj in partition 3

按Fj值大小排序，分区2 内节点重要度依次为14，5，4，13，11，6，7，8，10，12，分区2 内节点重要度依次为19，23，22，21，20。节点14 为分区2 内重要度最高的节点，且与退役同步发电机组A 距离较近，选取其作为分区2 的无功补偿接入点。节点19为分区3 内重要度最高的节点，但其距离退役同步发电机组B 距离较远。综合考虑补偿线路基建费用及无功线路损耗等因素，选取次重要节点23 作为无功补偿接入点。

退役同步发电机组接入筛选后的补偿节点，可为系统提供无功支撑，提高系统运行稳定性。

4 结语

采用节点间等值阻抗间接描述两点间电气距离，构成节点特征矩阵，可以清晰地描述节点与系统间耦合性强弱；应用层次聚类分析，可快速、准确地将系统节点按内部耦合特性划分为不同的分区。节点分区可简化退役同步机组作调相机运行时的无功补偿接入点筛选问题，缩小研究范围；根据地理位置确定退役同步发电机组所补偿分区，并通过计算分区内节点重要度指标，筛选出合适的无功补偿点。节点重要度指标可清晰地辨识节点在所处分区内的关键程度，指导筛选合适的接入点。