Ti-6Al-4V(ELI)合金在盐酸溶液中的电化学腐蚀行为及数值模拟
2021-09-24白彩云陈立杰
白彩云,赵 伟,石 炜,陈立杰
(1.厦门大学航空航天学院,福建厦门 361005;2.中国航发四川燃气涡轮研究院高空模拟技术重点实验室,四川绵阳 621000)
1 引言
Ti-6Al-4V(ELI)是航空航天领域使用最广泛的α+β钛合金,具有极高的比强度、良好的疲劳性能和耐腐蚀性,是航空发动机的重要结构材料,被广泛应用于压气机盘、叶片等承受大压力的结构件。钛合金良好的耐腐蚀性是因为其表面易形成一层致密的钝化膜,但钝化膜的性质、组成和厚度取决于环境条件。在实际服役过程中,钛及其合金在酸性环境中通常会被腐蚀,特别是在氯离子浓度较高的环境中,钝化膜受环境影响会发生破裂,进而受到的腐蚀作用更加明显[1]。
Ti-6Al-4V在各种恶劣环境和介质中的腐蚀行为已得到大量研究。其中,电化学阻抗谱(EIS)研究因不会对样品体系造成不可逆影响,且可得到较多的腐蚀动力学信息等优点,而得到越来越广泛的应用。Tsipas等[2]采用EIS法对Ti-6Al-4V在飞机模拟环境中的耐腐蚀行为进行了评估,指出在200℃下用NH4Cl 处理可以提高其耐腐蚀性。刘焱[3]研究了感应热处理后的Ti-6Al-4V及其焊缝在慢拉伸状态下的电化学行为,发现随着慢拉伸时间的增加,所有试样的容抗弧减小,耐腐蚀性降低。近年来,很多学者尝试通过有限元法对电化学反应进行数值建模,且已有许多成功的研究应用大型有限元分析软件COMSOL Multi-Physics 建模。如Deshpande[4]采用COMSOL 对镁合金腐蚀过程进行了数值模型,研究了围绕α相的连续β相和离散β相这两种微观组织结构的耐蚀性,认为当α相周围具有连续的β相网格结构时合金具有最佳的耐腐蚀性。
本文采用电化学实验和COMSOL Multi-Physics数值模拟相结合的方法,研究Ti-6Al-4V(ELI)合金在HCl 溶液中的电化学阻抗特性及极化曲线,并对合金α相和β相电偶腐蚀进行分析,研究结论可为高效分析合金材料的电化学腐蚀行为及机理提供依据。
2 电化学实验
2.1 实验材料及方法
实验材料为锻造成型Ti-6Al-4V(ELI)合金,其成分见表1。试样尺寸为15 mm×20 mm×5 mm。所有试样分别用320#、600#、1 000#、1 200#的SiC砂纸逐级打磨,并同时进行水冷。随后将试样放入乙醇中超声清洗10 min,再在水中漂洗,干燥,为后续实验做准备。

表1 Ti-6Al-4V(ELI)的化学成分(质量分数/%)Table 1 The main chemical composition of Ti-6Al-4V(ELI)(mass fraction/%)
采用CS350H 型电化学工作站三电极系统研究Ti-6Al-4V(ELI)合金在盐酸溶液中的腐蚀机理:Ti-6Al-4V(ELI)作为工作电极,铂电极作为辅助电极,Ag/AgCl作为参比电极。工作电极与电解质溶液的接触面积为1 cm2。实验均在室温(20~22℃)下进行。试样在进行电化学阻抗谱和极化曲线测试之前,均需经过相同时间的开路电位稳定,电化学阻抗谱交流幅值为10 mV,频率为10-2~105Hz。极化曲线扫描范围为-0.5~1.5 V(相对于开路电位),扫描速率为1 mV/s。实验进行三次,以保证实验的重复性。
2.2 实验结果与分析
2.2.1 电化学阻抗谱分析与讨论
图1 示出了Ti-6Al-4V(ELI)在w(HCl)=3.5%溶液中的EIS 测试结果,通过测量EIS 确定其等效电路,来推测电极系统中的腐蚀动力学过程及其机理。其中,Nyquist图表示阻抗的虚部与实部随扰动频率变化的趋势,其插图为用于EIS 分析的等效电路图;Bode图表明阻抗的绝对值和相位角随扰动频率变化的特征。可以看出,高-中频(101~105Hz)的圆弧表征该电极与法拉第反应有关的电荷传递阻抗,圆弧的直径越小,表示电荷传递的阻抗越低,材料的耐腐蚀性越差。

图1 Ti-6Al-4V(ELI)在w(HCl)=3.5%溶液中的EISFig.1 The EIS of Ti-6Al-4V(ELI)in w(HCl)=3.5%solutions
通过EIS分析,采用图1(a)中的电路图为拟合的等效电路。其中,Rs为溶液电阻,Rf为薄膜电阻,Rct为电荷转移过程遇到的阻力,Cdl为电极与电解质之间的电双层电容,CPE是常相位角元件。Rf和Rct与Ti-6Al-4V(ELI)合金的耐蚀性成正比,Cdl则相反。由于电极不是理想电容,工作平面会产生弥散效应,故等效电路中引入CPE来描述电容发生的偏离。CPE由CPE1和n来表示,当n=1 时CPE为纯电容。同时,相位角越偏离-90°,说明CPE越偏离理想电容。通过软件Zview对图1中的等效电路进行数值拟合,得到的参数如表2所示。

表2 Ti-6Al-4V(ELI)在w(HCl)=3.5%溶液中的EIS拟合结果Table 2 EIS fitting parameters of Ti-6Al-4V(ELI)in w(HCl)=3.5%solutions
根据钛合金与盐酸溶液反应的极化曲线可以看出存在钝化现象,钝化膜的主要成分为TiO2。为进一步表征钛合金的表面状态,可根据EIS 分析结果估算钝化膜的厚度[5],即:

式中:d为钝化膜厚度;C为钝化膜电容;ε为钝化膜介电常数,本文取εTiO2=100[5];δ为真空介电常数,δ=8.86×10-12F/m;S为表面积。
本文实验样品的S=1 cm2,C=2.97×10-5F,可得d=2.98 nm。Dai等[6]经过EIS的测量得到Ti-6Al-4V在w(HCl)=3.5%溶液中生成的钝化膜厚度为5.88 nm。相比较而言,相同质量分数的NaCl和HCl溶液,HCl溶液中的H+会进一步破坏钝化膜,从而降低了钛合金的耐腐蚀性能。
2.2.2 极化曲线分析与讨论
通过极化曲线表征材料极化过程中电极电位与电流密度之间的关系,电解质溶液中金属的腐蚀速率通过电化学反应动力学来确定。图2 所示为Ti-6Al-4V(ELI)在不同浓度HCl溶液中的极化曲线,其中I为电流密度。

图2 Ti-6Al-4V(ELI)在不同浓度HCl溶液中的极化曲线Fig.2 The polarization curves of Ti-6Al-4V(ELI)in different concentration of HCl solutions
根据Tafel 外推法可以得到腐蚀动力学参数——自腐蚀电位(Ecorr)和腐蚀电流密度(Icorr),再利用法拉第电解定律计算出Ti-6Al-4V(ELI)合金在电解质溶液中的腐蚀速率CR,结果如图3 所示。在HCl溶液中,随着HCl质量分数的增加,Ecorr越来越负,Icorr越来越大,Ti-6Al-4V(ELI)合金的腐蚀倾向越明显,腐蚀速率越快。

图3 Ti-6Al-4V(ELI)在不同浓度HCl溶液中的腐蚀速率Fig.3 Corrosion rate of Ti-6Al-4V(ELI)in different concentration of HCl solutions
3 电化学阻抗谱数值模拟
使用COMSOL Multi-Physics软件中的电分析接口和电极表面边界特征,来描述电化学反应方程。在电分析系统中,人为添加的电解质使电场强度维持在较低的状态,因此可以忽略溶液电阻。此时,可以使用扩散方程(菲克定律)描述系统中化学物质的质量传递,并利用合适的边界条件描述电极动力学和电容。
3.1 电化学模型
采用交流阻抗一维电分析模型。模型包含用于腐蚀单元的一维电解质域,域的长度L是基于扩散系数D和最低频率fmin的函数(式(2)),以便让物质有足够的扩散时间。

假设存在大量的电解质——这些电解质是电分析实验中所添加的惰性盐,可提高电解质的电导率,而不会干扰化学反应特性。在此假设条件下,溶液的电阻足够小,电场分布可以忽略不计[7]。从而,电分析接口可以实现对参与氧化还原反应的反应物和生成物的输运方程的求解。域方程为描述电活性物质化学输运的扩散方程,即为菲克第二定律。
此模型中,在工作电极表面(x=0),反应物质Ti发生氧化反应(失去电子)生成Ti4+:

Ti4+为还原方向的反应物,化学当量系数为-4,Ti为还原方向的生成物,化学当量系数为+4。
此外,还需设置边界方程。该反应的电流密度Iloc由描述氧化反应的电分析Butler-Volmer 方程给出:
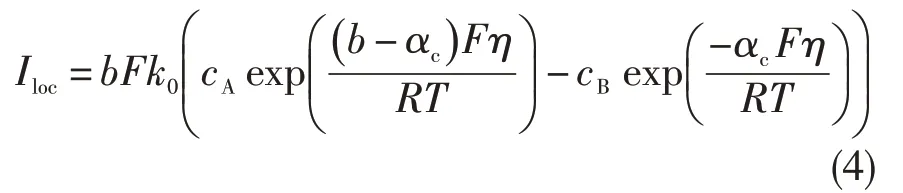
式中:F 为法拉第常数;k0为反应的非均相速率常数;αc为阴极传递系数;b为传递的电子数,b=4;cA(cB)为还原物(氧化物)的浓度,本体(x=L)中氧化物和还原物的浓度相同,均可表示为1 μM;η为工作电极上的过电位;R为气体常数;T为热力学温度。过电位是Ti 和Ti4+的氧化还原反应的外加电位Φs,ext与平衡电位Eeq之差。
在电极表面边界条件中,根据法拉第电解定律,反应物和生成物的通量与所得的电流密度成正比,因此:

采用交流阻抗模块,为施加在特定直流电压上的谐波扰动(频率为w)建模。本文中施加的外加电位是氧化还原反应的平衡电位:

这一扰动的幅值ΔΦ相对于RT/F来说较小,因此边界方程可以进行线性化处理,系统对扰动产生线性响应,并且物质通量、浓度分布和电流密度也在相同频率下受到正弦扰动的影响。
本研究中,扰动频率在10-2~105Hz 之间变化,针对基于初始电压的扰动进行求解。在每个频率下,使用频域形式的菲克第二定律作为控制方程。求解的前提条件是:主体浓度满足ci,1=0,且电极表面满足Φs,ext=ΔΦ。
3.2 电化学阻抗模拟结果与分析
EIS 电化学模型的数值模拟中,输入的参数如表3 所示,根据提供的参数在频率范围内进行线性扰动,解析阻抗对频率的响应。

表3 COMSOL模型的输入参数Table 3 Input parameters for the COMSOL model
图4 所示为Ti-6Al-4V(ELI)合金在w(HCl)=3.5%溶液中的Nyquist图。可以看出,COMSOL模型计算结果与实验数据吻合较好,在低频时质量传递占主导地位,在高频时向动力学控制过渡。与图1的实验结果相比,COMSOL 模型结果在低频区显示出更精确的阻抗值,而在中频区数值略高,在高频区表现一致。

图4 COMSOL模型模拟的EIS与实验EIS的对比Fig.4 The comparison of COMSOL model simulated EIS and experimental EIS
通过软件Zview 对COMSOL 模型模拟的EIS 进行拟合,得到C=2.14×10-5F,因此其钝化膜厚度为4.14 nm,与电化学实验估算值的相对误差为38.9%。由于COMSOL模型为理想状态的Ti-6Al-4V(ELI)合金与盐酸溶液的理想电化学发应,而实际实验过程中非理想合金材料与盐酸的反应更为复杂,加之对钝化膜的实验测试相对较困难,故认为数值模拟结果可为对比合金在不同溶液中生成的钝化膜厚度提供依据。
4 α和β两相腐蚀模拟
对Ti-6Al-4V 合金α和β两相腐蚀的数值模拟,使用COMSOL Multi-physics中的任意Langrangian-Eulerian(ALE)应用模式[4]。该方法用Nernst-Planck方程和Laplace方程作为电分析和传质控制方程,采用动电位极化曲线作为边界条件。本文用实验获得的Ti-6Al-4V 合金α相和β相的极化曲线数据作为边界条件求解Nernst-Planck方程,得到系统的电位分布和电流密度。
4.1 数学模型[4]
通过求解电解质溶液中的电流和电位分布获得电极表面的电流密度,模型中物质i 的迁移可以用Nernst-Planck方程来表示,即:

式中:Ni为通量,zi为电荷数,ui为迁移率,Φ为电解质电位,U为溶剂速度。
电解质溶液中,物质i质量守恒可以表示为:

在此模型中,假设:①电解质溶液混合良好,不存在浓度梯度;②溶剂是不可压缩的;③溶液是电中性的;④溶解反应发生在阳极表面,而析氢反应发生在阴极表面。根据以上假设,方程(8)可以简化为:

上式采用了电势的Laplace方程形式,代表了腐蚀速率的上限。在电解质域中求解方程(9)还受边界条件的约束。阳极表面与阴极表面的边界条件分别为:

式中:σ为电解质溶液的电导率,Ia(Φ)为阳极的电流密度,Ic(Φ)为阴极的电流密度。
Ia(Φ)和Ic(Φ)是分段线性插值函数,可以分别从β相和α相的极化实验中得到。将绝缘边界条件应用于电解质域的其他边界。
图5 所示为β相和α相在5M HCl 溶液中的极化曲线。为了保证实验的可靠性,两组极化实验的环境必须一致,因此选择近β 型钛合金TMZF(Ti-13Mo-7Zr-3Fe)为β 相[9],一种近α型钛合金Al-Ti[10]充当α相。通过TMZF和Al-Ti分别在5 M HCl溶液中的极化曲线得到电流密度(Ia(Φ)和Ic(Φ))与阳极和阴极电位之间的关系。从图中可以得到,α型钛合金(Al-Ti)的自腐蚀电位为-0.239 V,β型钛合金(TMZF)的自腐蚀电位为-0.450 V,因此β相的自腐蚀电位比α相的自腐蚀电位负0.211 V。

图5 TMZF(β钛合金)[9]和Al-Ti(α钛合金)[10]在5 M HCl溶液中的极化曲线Fig.5 The polarization curves of TMZF(b-titanium alloy)[9]and Al-Ti(a-titanium alloy)[10]in 5 M HCl solution
根据边界条件求解Laplace方程(9),得到阳极和阴极表面各节点的电位、电流密度分布。再利用法拉第定律根据电流密度计算腐蚀速率,并将ALE移动网格技术应用于腐蚀过程中移动界面的计算。假设阴极不发生反应,则阴极表面的移动速度可认为是0,其他边界位移也都是0。将ALE 方法与COMSOL Multi-physics相结合,来求解网格位移。
β相和α相的横截面微观结构模型的几何图如图6所示。微观结构可由水平集函数L以自变量x和y 表示为micro(x,y)[4],表示同一边界上ΦL>0时的阳极表面和ΦL≤0时的阴极表面。β相由ΦL>0的区域表示,α相由ΦL≤0的区域表示。当插值水平集函数L的值分别为0 和1 时,可识别电极边界为β相和α相。

图6 Ti-6Al-4V合金包含β相和α相的横截面微观结构模型Fig.6 Geometrical model of microstructure of Ti-6Al-4V containing b phase and a phase
4.2 数值模拟结果与腐蚀机理分析
从极化曲线可以看出,同等面积比组成的α相和β相,溶解反应发生在阳极表面(β相),析氢反应发生在阴极表面(α相)。此模型描述的阴极边界由于负电流密度进入电解质溶液中的沉积过程没有物质的损失或积累,因此假设无腐蚀过程的阴极表面在电解质溶液中发生析氢反应是合理的。
使用二次电流分布接口根据以下表达式求解电解质域上的电位:

式中:Ii1为电解质电流密度矢量。
电极表面法向上的溶解速度计算依据为:

式中:Mi为物质i的摩尔质量,MTi=47.87 g/mol;ρi为腐蚀物质的密度,ρTi=4.54 g/cm3;Rdep,i,m通过方程(14)计算。

式中:ui,m为化学当量系数,取18[11];bm为参与电极反应的电子数量,取4。
图7示出了腐蚀电位的数值模拟结果。从图中可以看出,β相的电位比α相的电位低,在电解质溶液中优先被溶解,而α相未被腐蚀。

图7 腐蚀电位的数值模拟结果Fig.7 The numerical results of corrosion potential
通过电极动力学表达式来模拟电极表面β相的电极反应。电极表面β相的局部电流密度设为:
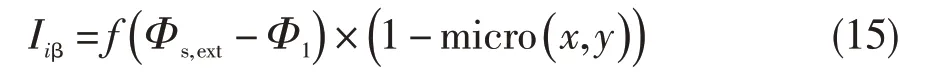
通过分段三次插值函数将电极表面β相的局部电流密度与电解质电势导入极化实验数据中,得到如图8所示的电流密度数值模拟结果。从图中可以得到β相的电流密度为2.8×10-5A/cm2,大于α相的电流密度,因此β相更容易被腐蚀。Shukla 等[12]和Me⁃tikos-Hukovic等[13]提出,Ti-6Al-4V表面生成的钝化膜包含氧化钒,而氧化钒具有有限的防腐作用,在盐酸溶液中易于溶解,V 元素又聚集在β相,因此β相更容易被腐蚀。本文数值模拟情况与其一致,证明了此数值模型的正确性。

图8 电流密度数值模拟结果Fig.8 The numerical results of current density
为研究Ti-6Al-4V(ELI)合金中β相对合金腐蚀的影响,通过法拉第电解定律得到β相在5M HCl溶液中的腐蚀速率为:

式中:F≈96 485 C/mol。
数值模拟得到的β相的腐蚀速率约为7.65×10-10m/s。根据图3 测试结果,Ti-6Al-4V(ELI)合金在5 M HCl溶液中的腐蚀速率约为1.63×10-9m/s,约为模拟得到的β相的腐蚀速率的2.13倍。这是由于合金材料中不可避免地存在缺陷,加之参比电极不同等因素影响,使得数值模拟得到的β相的腐蚀速率较低。但数值模拟结果仍可以快速地为Ti-6Al-4V(ELI)合金在腐蚀环境中的腐蚀评估提供数据支持。
5 结论
采用实验和数值模拟相结合的方法,分析了Ti-6Al-4V(ELI)合金在HCl 溶液中的电化学腐蚀行为及腐蚀机理,主要结论如下:
(1) 通过实验测试得到了Ti-6Al-4V(ELI)合金在w(HCl)=3.5%溶液中的电化学阻抗谱,采用等效电路拟合得到阻抗数据,并根据阻抗数据进一步估算出钝化膜厚度为2.98 nm;得到了Ti-6Al-4V(ELI)合金在不同浓度HCl 溶液中的极化曲线及腐蚀速率。
(2) 利用COMSOL Multi-Physics进行钛合金的电化学腐蚀行为数值模拟,得到了Ti-6Al-4V(ELI)合金在w(HCl)=3.5%溶液中的电化学阻抗谱及钝化膜厚度。模拟结果与电化学实验结果吻合较好,为对比合金在不同溶液中生成的钝化膜厚度提供了依据。
(3) 利用COMSOL 建立了研究Ti-6Al-4V(ELI)合金α相和β相腐蚀的ALE 模型,得出β相的电流密度比α相的大,β相更容易被腐蚀,β相在5M HCl 溶液中腐蚀速率约为7.65×10-10m/s。此数值模拟结果可快速地为Ti-6Al-4V(ELI)合金在腐蚀环境中的腐蚀评估提供数据支持。
