涡轮盘热处理过程温度场数值研究
2021-09-24吴超,黄兴
吴 超,黄 兴
(中国航发湖南动力机械研究所,湖南株洲 412002)
1 引言
涡轮盘是航空发动机的重要热端部件,在其毛坯件热处理过程中,温度场变化对于涡轮盘性能有十分重要的影响。温度分布的不均匀性会造成热处理过程中产生残余应力,而其变化速率又会改变微观组织结构,影响盘件的力学性能[1-2]。为此,涡轮盘热处理过程中传热及温度场变化规律的研究日益受到重视。
针对温度和保温时间等对材料组织结构方面的影响已经开展了较多的研究[3-5],而随着计算机技术的发展,数值仿真也被越来越多地应用于热处理过程研究中。崔磊等[6]介绍了热处理数值模拟的多场耦合理论,并针对国内外主流数值模拟软件进行了详细分析;余磊等[7]采用有限元分析软件,对焊接转子热处理过程中残余应力的释放行为进行了数值研究;Dong 等[8]对焊缝热处理残余应力的释放机理进行了分析。这些研究大都偏向于热处理过程中结构应力的分析,而多场耦合分析时,温度场计算是应力分析的基础,准确计算温度场十分重要。为计算热处理的传热过程,通常采用三类边界条件[9],但工艺变化如自然空冷变为强制风冷时,多采用经验公式或依据经验给定换热系数的相对变化量来计算温度场[10-12]。这种方法虽然可以满足一般分析,但工艺流程和盘件表面几何变化较大时,其精度也会存在一定的局限。
为提高热处理过程中温度场计算的精度,本文开展了流场/温度场一体化建模方法研究,分析了涡轮盘毛坯在包含空冷、风冷、淬火等多个工艺过程下的流场变化及流场/热耦合过程,研究了工艺流程变化对涡轮盘温度场的影响,以及复杂工艺流程下的温度场变化规律,可为涡轮盘热处理过程分析及工艺改进提供参考。
2 几何模型
涡轮盘毛坯件为旋成体结构,其根部较厚,中间及外缘相对较薄,中心有通孔,对称面几何见图1。

图1 几何模型及温度特征采样测点位置Fig.1 Geometric model and temperature sampling point locations
涡轮盘毛坯件热处理过程分为3 个阶段,包含转运、风扇吹风冷却(即风冷)和淬火过程。从炉中转运过程可视为空气中的自然冷却(即空冷)。风冷时涡轮盘水平放置在工装上,单风扇布置在距毛坯件中心轴2.0 m 位置,气流沿水平方向吹掠涡轮盘,同时毛坯件以一定速度绕轴线逆时针旋转。
为对比涡轮盘毛坯件温度变化规律,在对称面中心线布置温度特征采样测点,并依次编号(图1中A1~A5,B1~B5)。另外,盘件内、外壁面也分别编号(图1中A6,A7),以对比其温度变化过程的差异。
热处理过程的工艺流程及基本计算参数见表1。此外,涡轮盘材料的比热容和导热率与温度相关,淬火油的比热容和密度也是温度的函数,这些热物性参数均以分段线性插值的方式在计算中考虑。
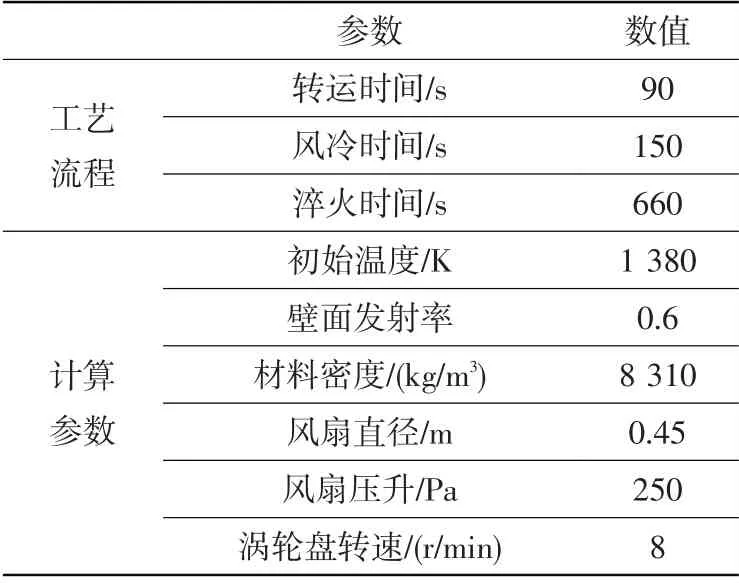
表1 热处理过程的工艺流程及计算参数Table 1 Process flow and calculation parameters of heat treatment
3 数值模型
3.1 网格划分
热处理时高温涡轮盘与低温流体进行热传递。针对冷却过程,建立包含涡轮盘固体区域和空气、淬火油等流体计算域的网格模型,固体和流体域热量通过固体壁面耦合迭代与参数交换,无需设定换热系数。对计算域空间进行剖分,全部生成六面体结构化网格。考虑到涡轮盘靠近表面区域温度梯度大、流态复杂,对壁面附近的固体和流体网格均进行加密处理。计算网格共计168 万,其中对称面和盘件表面网格如图2所示。
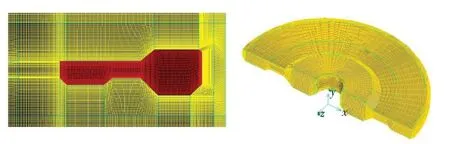
图2 计算网格Fig.2 Computational grid
由于热处理不同阶段计算模型有所变化,为统一起见,建立一套计算网格,但边界条件根据实际工艺变化调整。
3.2 数值模型
空冷自然对流计算时,采用Boussinesq 模型计算动量方程的浮力项:
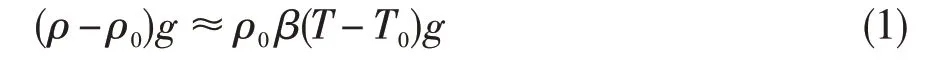
式中:ρ0为参考密度,T0为操作温度,β为气体的热膨胀系数。
风冷过程中,采用风扇模型模拟风扇风场。风扇被认为是由无限小且不连续的作为速度函数的压升组成:

式中:Δp为压升,fn为压力跳变的多项式系数,v为垂直于风扇截面的局部流体速度。
流场控制方程为微分形式的N-S方程,包括:
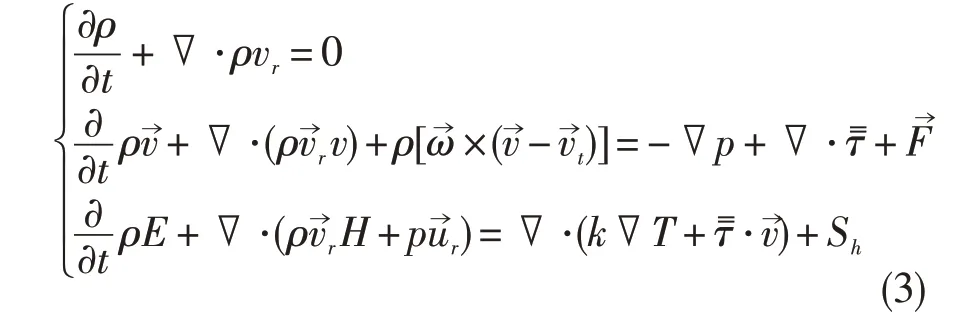
另外,采用参考坐标系法模拟风冷过程中盘件旋转运动的影响,采用离散坐标模型(DO)计算涡轮盘高温表面的热辐射。
基于有限体积法,采用与时间相关的耦合隐式解法求解控制方程。控制方程中的扩散项、对流项分别采用二阶中心差分格式和二阶迎风格式离散。
4 计算结果及分析
4.1 流场特征分析
涡轮盘冷却过程中,高温壁面热量除通过热传导和热辐射散失外,还包含自然对流及强制对流换热过程,流场变化对热交换会产生较大影响。图3给出了不同冷却过程中涡轮盘周围流场速度的典型分布,可见不同冷却过程中的流场速度和流态均有较大差异。空冷过程中,高温盘件对周围气流加热,气流密度减小从而产生了对流运动。涡轮盘底部气流不断受到盘件加热,沿中心孔和绕盘件外缘上升。同时,由于中心区域流速大、压力降低,绕过外缘的气流向中心汇聚,并在涡轮盘上壁面局部诱导出回流区。回流区气流在上升气流的摩擦力剪切作用下回旋运动,自然对流时盘件周围最大流速在2.0 m/s以内。风冷过程中,高速气流从左侧吹过涡轮盘件表面,流线在迎风面后向上、向下偏转,绕过涡轮盘边缘时因局部流道扩张而速度增大。在盘件表面的局部区域、中心孔区域形成低速涡流区,受高速主流的剪切产生回转流动。在背风侧,由于气流局部突然扩张产生分离,背风区域气流速度很低,分离区气体受上、下壁面较高速度气流的剪切作用而形成两个方向相反的涡流,高速气流经过分离区一段距离后汇合。淬火过程中的流场与空冷过程中的相似,此时最大流动速度仅约0.3 m/s,且淬火油黏性较大,绕过涡轮盘外缘的流体基本贴着上壁面向中心汇聚,上升过程中速度分布也更复杂。
上述流场速度分布是冷却过程中的典型分布样式,采用非定常计算得到的流场速度有一定的周期性变化,与实际散热过程中的一致。
4.2 冷却方式影响分析
4.2.1 风冷和空冷对比
以空冷90 s 温度场为初始状态,分别按照空冷和风冷150 s(即结束时刻240 s)计算盘件温度变化,研究两种工艺对温度场的影响。
表2 给出了两种冷却方式下采样点150 s 内的温度平均下降速率。可见,A1和A6点温度下降很慢,这是由于热处理初始时刻盘件表面温度高,散热以热辐射为主,这两个采样位置接近内壁面,难以向外部环境辐射热量,而通过周围空气对流散热效率较低所致。A2点为毛坯件几何厚度最大处,温度下降速率也较慢。A3~A5点结构厚度较小,温度下降速率相对较快。从空冷和风冷的对比看,风冷时因盘件表面对流换热强度增大,不同采样点温度下降速率均高于空冷情况。特别是风冷时中心孔气流在外部高速气流剪切下运动(图3(b)),增加了内孔处的换热系数,A1点温度下降速率明显提高。采样点越靠近盘件外缘,由于对流换热系数增加且结构尺度较小,其温度下降速率越高,A5点风冷温度下降高达228.01 K。从两个方案的温度下降值差值也可看到,A7点温度下降速率差异最大,而A2点差异最小。

表2 风冷和空冷采样点温度平均下降速率对比Table 2 Comparison of average temperature drop rates of air cooling and wind cooling
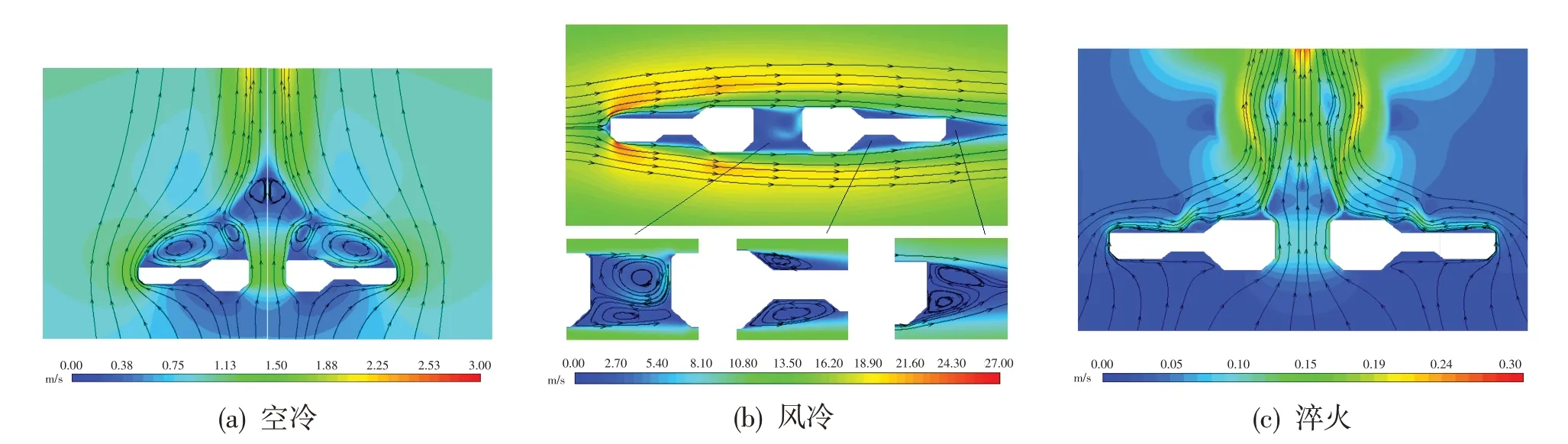
图3 不同冷却过程中涡轮盘周围流场速度Fig.3 Flow field velocity around turbine disk during different cooling processes
图4 对比了240 s 时风冷和空冷的盘件截面温度分布。可以看到,与表2 中采样点反映的规律相同,风冷时涡轮盘温度明显比空冷时的低,且在轮盘外缘结构厚度较薄位置,尤其是靠近外壁面处温度更低。风冷时整个截面的温度梯度也比空冷时大。
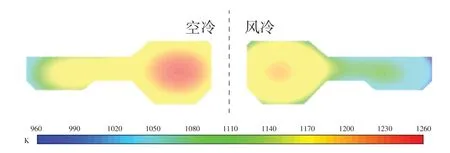
图4 两种工况240 s时涡轮盘对称面温度分布Fig.4 Temperature distribution of symmetrical surface of turbine disk under two conditions for 240 s
4.2.2 盘件旋转影响
分别针对盘件固定和绕中心轴旋转(转速8 r/min)两种方案,仍以90 s 空冷后的温度分布作为初值,计算风冷150 s(即结束时刻240 s)的温度场。
从表3 中的采样点温度看,盘件绕中心轴旋转时,两侧相对位置采样点温度基本一致,最大温差在2.5 K以内。涡轮盘固定时,两侧相对位置采样点温度差异较明显。如迎风侧采样点A5与背风侧采样点B1之间的温差高达179.36 K。此外,B1点的温度反而比A1点的低,这是由于中心孔涡流区在靠近B1点位置流速大、局部换热效率高所致(图3)。
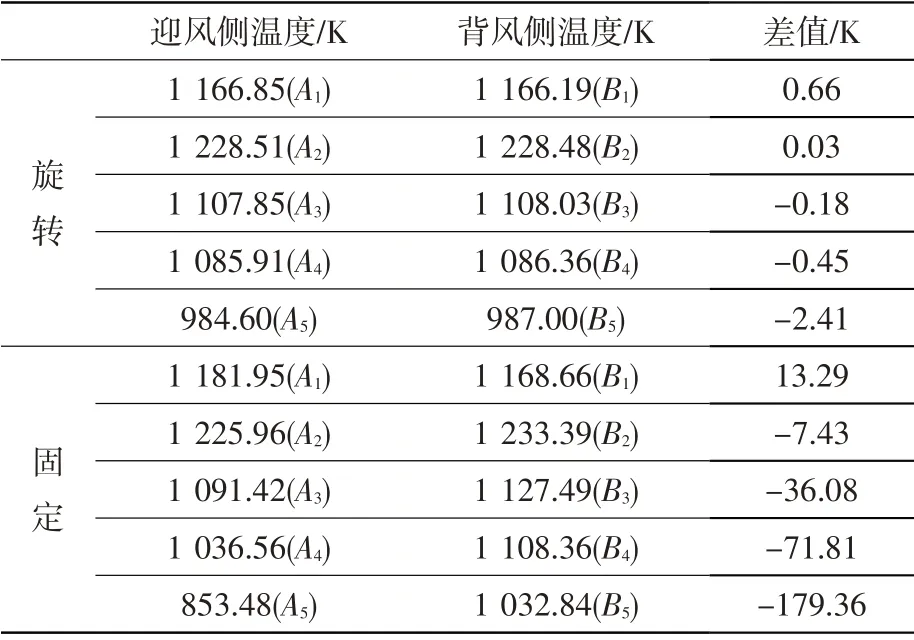
表3 涡轮盘旋转和固定时采样点温度对比Table 3 temperature comparison of sampling points for rotating and fixed turbine disk
图5对比了两种冷却方式下涡轮盘截面的温度分布。显然,盘件旋转时两侧截面温度分布接近,而盘件固定时迎风侧(左侧)靠近外缘的温度明显低于背风侧(右侧),迎风侧温度梯度也显著增加。
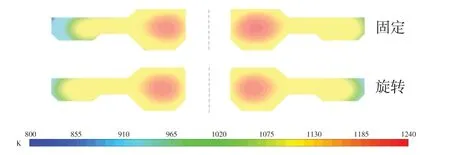
图5 两种工况240 s时涡轮盘对称面的温度分布Fig.5 temperature distribution of symmetrical surface of turbine disk under two conditions for 240 s
对应于温度分布,图6 给出了沿中心特征线的温度变化。可以看出,盘件内、外壁面附近温度梯度较大。盘件旋转时左右两侧曲线基本对称,而盘件固定时右侧温度高于旋转工况,左侧温度低于旋转工况,且越靠近外缘差异越明显。通过盘件的旋转可以提高涡轮盘冷却过程中截面温度的一致性。
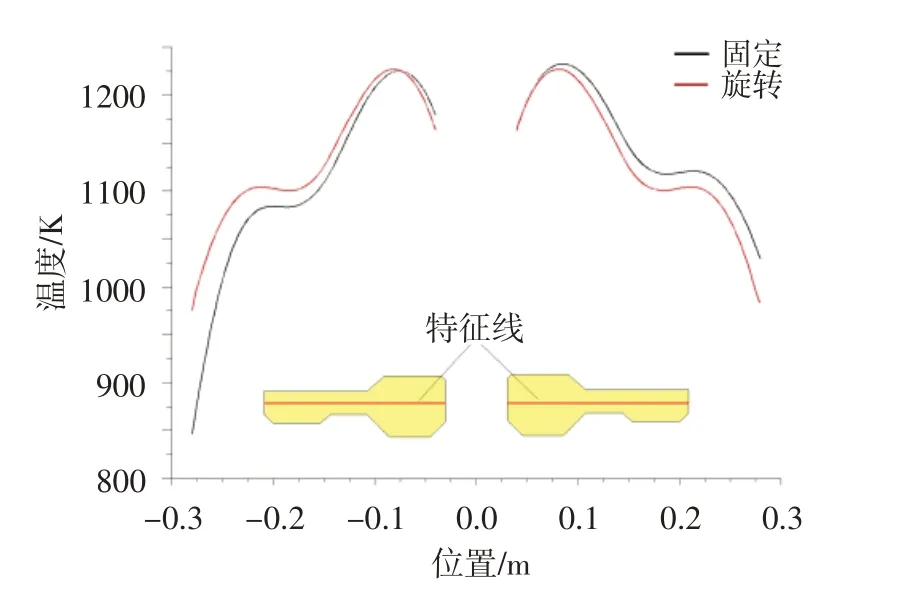
图6 两种工况240 s时沿中心特征线温度Fig.6 Temperature along the central characteristic line under two conditions for 240 s
4.3 冷却过程分析
针对涡轮盘毛坯件热处理的3个工艺过程开展仿真分析。图7给出了直接由流场和温度场耦合计算得到的4个特征表面的换热系数。从曲线变化看,换热系数根据工艺流程分为了3个阶段。空冷阶段换热系数最小,风冷时有所增强,淬火时最大,且每个阶段内换热系数均随时间呈下降趋势。在空冷和风冷阶段,B、C和D截面换热系数差异不大,这是由于此时盘件表面温度高,热量主要以热辐射的方式向外散失,对流换热损失的热量比例较小;A截面换热系数明显较小,其原因是A截面位于中心孔处,难以向环境辐射热量。淬火阶段,不同特征面之间流态差异,以及壁面本身与淬火油之间温差,对换热系数都会有影响。此时A截面处于通流状态,其换热系数也较高。随着时间的增加,换热系数不断减小,且盘件表面温度下降后,总换热量也会显著降低。

图7 换热系数随时间的变化Fig.7 Variation of heat transfer coefficient with time
图8 和图9 分别给出了热处理过程中采样点温度及其下降速率随时间的变化。可见,根据工艺过程不同,曲线均明显分为三个阶段。整个热处理过程中A2点的温度比其他采样点的高,A5和A7点的温度则显著低于其他采样点。900 s时,A5和A7点的温度降低到350 K左右,曲线变化速率已很小,而A2点的温度还有约600 K,仍然有较大的下降速率。总体而言,热处理开始时各采样点的温差较小,但随着时间的增加不同采样点的温度均有差异,表明整个过程中均存在一定的温度梯度。
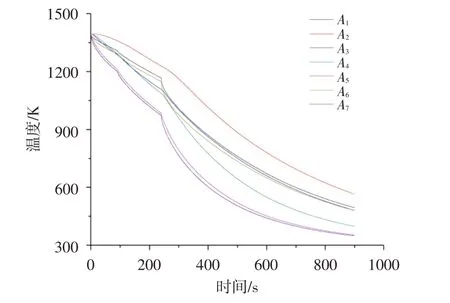
图8 采样点温度随时间的变化Fig.8 Variation of temperature at sampling point with time

图9 采样点温度下降速率随时间的变化Fig.9 Variation of temperature drop rate at sampling point with time
图9中温度下降速率的阶段性十分明显。当冷却方式转换时,除A2点外的采样点温度下降速率均有较明显的增加,尤其是淬火过程中换热系数高,淬火开始时温度下降速率最大,之后曲线逐渐转平。这与图7的换热系数变化相对应。随着换热系数的减小和壁面温度的降低,总的散热量减小,温度下降速率也降低。A2点温度在初始时刻因传热的稳定状态还未建立而基本不变,直至盘根区域建立一定温度梯度后才逐渐下降。而且外部冷却方式变化对A2点的影响相对较小,其温度下降速率曲线没有产生跳动。此外,A5、A7点分别为外缘特征点和壁面,风冷过程中盘件以一定的速度转动,采样点会周期性地在迎风侧和背风侧之间转换,因此换热量也会产生波动,其温度下降速率在周期性波动中逐渐减小,这与理论分析相吻合。
5 结论
(1) 热处理过程温度场变化与流场相互耦合,不同工艺阶段冷却方式不同,流场参数分布和流动特征也有较大差异。
(2) 相对于空气自然冷却过程,采用风扇强制冷却能显著增加对流换热的强度,提高换热效率,但也会增加盘件的温度梯度。
(3) 风冷过程中,采用旋转涡轮盘的方法,可以在单风扇非对称流场中有效增加盘件截面温度的一致性。本文研究的涡轮盘以8 r/min 的转速旋转即可实现较好的温度一致性。
(4) 不同工艺阶段,盘件不同区域温度下降速率不同,根据位置变化呈现出一定的数值差异。
(5) 基于流场/温度场的一体化建模和仿真,能反映热处理过程中的温度场变化规律以及其中的非定常效应,根据流场与固体域温度场耦合关系计算不同表面换热系数,避免了采用经验公式给定热分析边界条件可能带来的误差,可为复杂结构热处理温度场分析及工艺改进提供参考。
