充分利用表象，使学生经历数学化

俞宏毓 朱向阳

摘要：数学学习应该是不断数学化的过程。教师教学可以根据布鲁纳的“从实物操作到表象操作再到符号操作”认知理论，设计数学化的过程。其中，特别需要重视半具体、半抽象的表象操作的中介作用。教学《数图形的学问》一课时，尝试充分利用表象，使学生经历数学化。反思这节课的教学过程，可以得到如下教学启示：情境设置要能促进学生的理解;启发式教学不会过时;要使不同的人在数学上得到不同的发展。

关键词：数学化;表象;《数图形的学问》

数学化是荷兰著名数学家和数学教育家弗赖登塔尔提出来的。他认为，“用数学方法把实际材料组织起来就叫数学化”，学生应该学习数学化，而且是从最低的层次开始，也就是先对非数学内容进行数学化（属于横向数学化）。张奠宙先生认为，人们在观察、认识和改造客觀世界的过程中运用数学的思想和方法来分析和研究客观世界的种种现象并加以整理和组织的过程就是数学化，“让学生学会数学地思考与研究各种现象，形成数学的概念、运算和法则，构造数学模型，经历一个数学化的过程”是理所当然的。很多研究认为，数学学习应该是不断数学化的过程，学会数学化是养成数学学科核心素养的关键。

关于如何进行数学化，张奠宙先生指出，“数学化是一个过程，是一个从问题开始，由实际问题到数学问题，由具体问题到抽象概念，由解决问题到更进一步应用的教育全过程”。顾泠沅先生认为，数学化就是在具体，半具体、半抽象，抽象之间的铺排，是穿行于实物与符号之间的形式化过渡，因而可以根据布鲁纳的“从实物操作到表象操作再到符号操作”认知理论，设计数学化的过程。例如，教学“退位减法”时，让学生经历“从摆小棒到用计数器再到减法公式”的数学化过程。再如，教学“有余数的除法”时，让学生经历“从实际分豆子到脑中分豆子再到除法公式”的数学化过程。又如，教学“长方形和正方形的面积”时，让学生经历“从实际数格子到脑中数格子再到面积公式”的数学化过程。因此，顾泠沅先生特别强调半具体、半抽象，即表象阶段在数学化过程中的重要作用，认为表象操作是从实物操作到符号操作的中介。教师要充分利用表象，使学生经历数学化。

教学北师大版小学数学四年级上册“数学好玩”实践活动单元中的“数图形的学问”专题时，教师便尝试充分利用表象，使学生经历数学化。

一、课前思考

“数图形的学问”和三年级上册的“搭配中的学问”、六年级上册的“比赛场次”属于一个系列，都是简单的组合问题。小学阶段简单组合问题的学习可以为高中阶段排列组合知识的学习打下基础。三个专题呈现出从简单到复杂、从具体到抽象的变化趋势。“数图形的学问”起着承上启下的作用。

“数图形的学问”教材从“鼹鼠钻洞”的情境出发，让学生思考鼹鼠有几条跑动路线，引入4点组合问题。该情境的设置非常巧妙：4个洞在一条直线上。因此，教师可以引导学生在一条直线上取点（代表洞）数连线段（代表路线），让学生经历从“求鼹鼠跑动路线条数”到“数线段条数”再到“列式计算”的数学化过程。教学过程中，可以紧紧抓住“数线段条数”这个表象阶段，使学生充分理解简单的组合问题，不难解决更复杂的组合问题，出现错误也能及时发现。

二、课堂流程

（一）情境引入

给出教材情境后，教师先引导学生读懂题意，关注鼹鼠钻洞的方向性，防止解题出错——

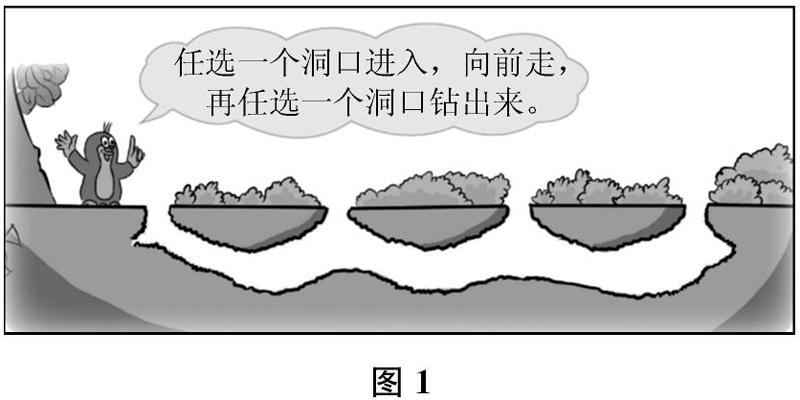
师 （出示教材情境图，如图1）你读懂了什么？来说说看。

生 小鼹鼠可以选一个洞进去，但是不能从进去的洞出来。

生 鼹鼠从第二个洞进去的话，不可以从第一个洞出来。

师 你是从哪里看出来的？

生 题目说向前走，从第一个洞里出来就是向后走了。

师 那我们给它定个方向，（同步指图）这边是左边，这边是右边。小鼹鼠从左边的洞钻进去后，就只能从右边的洞钻出来。

（二）从求路线条数到数线段条数的数学化

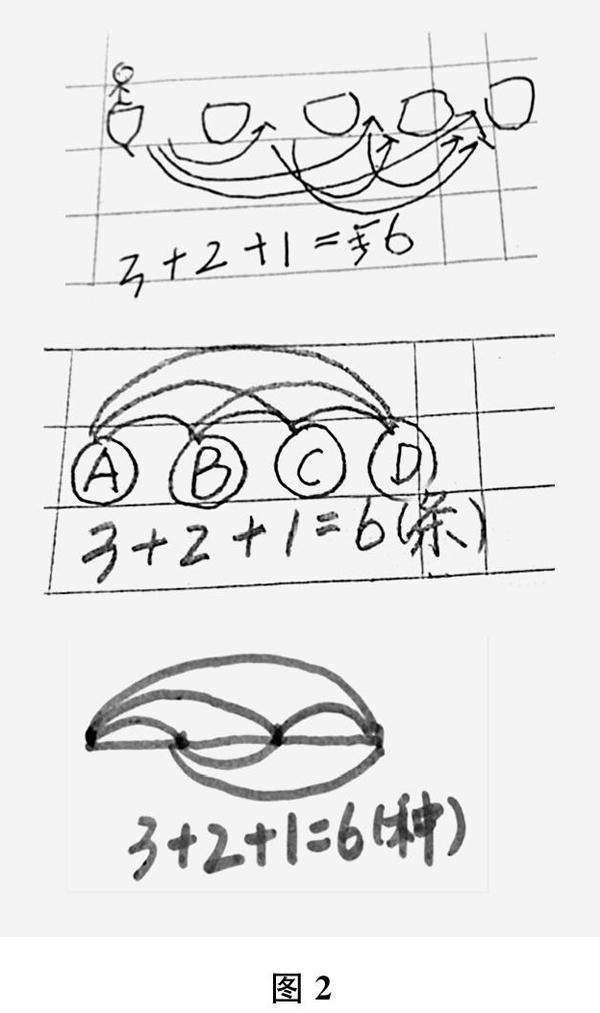
在自主尝试求路线条数的过程中，学生出现了“在情境图上画并数路线”“画示意图并数路线”以及“直接列式计算”等多种方法。其中，画示意图的方法占大多数，并且主要有如图2所示的三种方法。

教师抓住这半具体、半抽象的表象阶段，展示如图2所示的三种画示意图的方法，让学生观察“哪一种图更简洁、更方便”，引导学生聚焦画线段图的方法。然后，引导学生关注现实与表象的要素之间的“一一对应”，经历从求路线条数到数线段条数的数学化——

师 知道怎么由情境图画线段图吗？

生 知道。

师 先画什么？（稍停）用一条直线来表示地平线，然后用什么来表示洞？

生 一个圆圈。

生 一个点。

师 情境图中小鼹鼠挖了几个洞？

生 4个洞。

师 那就在地平线上点几个点？

生 4个点。

师 每一个点表示什么？

生 一个洞。

师 那么寻找有几条路线就变成了什么问题？

生 数线段。

师 为什么变成了数线段的问题呢？比如说洞口A、洞口B、洞口C、洞口D，如果从洞口A进去，可以从洞口B出来，也可以从洞口C出来，还可以从洞口D出来。也就是说，A到B的这条线段表示的意思是什么？

生 一条跑动的路线。

师 所以，有几条这样的线段就有几条跑动的路线。

（三）强调数线段条数的顺序

在自主尝试数线段条数的过程中，学生出现了如图3所示的两种顺序的数法。

数线段条数时的顺序对于不出错，即不数重、不数漏（尤其是遇到点比较多的情况时），以及发现规律，从而列式计算，都具有重要的意义。因此，教师让两个学生分别展示两种顺序的数法，启发学生总结数的规律，从而强调数的顺序——

师 我发现同学们在数的时候都没有多数或少数，为什么？你们是怎么做到的？

生 因为我们是有规律地数的。

师 用什么规律数？

生 从点……

师 （指着图3中的第一种数法）比如说从点出发的时候，是怎么样数的？

生 从左到右。

师 而不是数完点A了，就数点C，再数点B，等等。也就是说，是按照顺序来数的。（指着图3中的第二种数法）按段来数的时候，也是有顺序的：先数一段的，再数两段的，接着数三段的。总的来说，我们在数的时候做到什么就不会乱、不会错？

生 按顺序数。

师 对，按顺序数，就不会重复，也不会遗漏了。

（四）从数线段条数到列式计算的数学化

通过数线段条数解决了“鼹鼠钻洞”的4点组合问题后，教师展示“菜地旅行”的情境，让学生通过数线段条数解决“有5个站点的单程车要准备多少种车票”的5点组合问题。然后，进一步延伸到更多站点的情况，激发学生的认知冲突，引导学生从递推的角度发现数量增加的规律，理解列式的原理，从而经历从数线段条数到列式计算的数学化——

师 5个站点有10种票。那老师再进一步：路线上又开辟了一个新的站点，有6个站点，你知道有多少种车票吗？谁能很快得出结果？

生 有15种车票。

师 你是怎么得到的？

生 因为多了一个站点，所以从原来那些站点出发或到原来哪些站点的车票都要再加1。

师 所以要比原来增加几种车票？

生 5种。

师 所以可以用算式怎么表示？

生 5+4+3+2+1。

……

师 那10个站点的时候应该怎么写？

生 9+8+7+6+5+4+3+2+1。

师 非常棒！15个站点呢？

生 14+13+12+11+10+9+8+7+6+5+4+3+2+1。

师 是的。找到规律，列出算式，接下来就是怎么算的问题了，是不是啊？那么下次我们可以继续探讨对这样的算式，怎样又快又准地算出得数。

（五）三个拓展

实现了从数线段条数到列式计算的数学化后，教师对问题进行了三个拓展，开拓了学生的视野和思路，并且为后续内容的学习做好了铺垫。

第一个是内容上的拓展，从简单的组合问题拓展到简单的排列问题，设置了“有8个站点的往返车要准备多少种车票”的问题。

教学过程中，学生出现错误时，教师征询不同的意见后，再次引导学生回到数线段条数的活动中，寻找“乘2”的意义——

师 谁来汇报一下？

生 7+6+5+4+3+2+1=28。

师 是28种吗？有没有不同的意见？

生 我觉得这里应该乘2，因为它求出的只是单程的票数。

师 你从哪里看出来要乘2？从哪里看出来跟我们刚才的车票问题是不一样的？

生 往返。

师 那么为什么往返时乘2就可以了呢？（稍停）我们可以倒回去再数一遍线段条数。

……

第二个是形式上的拓展，从一维的数线段问题拓展到二维的数平面图形问题，设置了求图4中平行四边形个数的问题。

教学过程中，学生顺利求出平行四边形的个数后，教师引导学生发现等价性，把数平行四边形的问题转化为数线段的问题，理解问题的本质——

师 你怎么知道是4+3+2+1的，请你说说4在哪？

生 4就是一个一个的平行四边形有4个，3就是两个两个的平行四边形有3个，2就是三个三个的平行四边形有2个，1就是四个四个的平行四边形有1个。

师 你是用什么方法来数的？

生 按段的方法。

师 那我们能不能按点的方法来数？可以把这幅图怎么样？

生 画成线段。

师 对，我们可以把它变成一条线段。那么，把这些斜着的边都压缩成了一个一个的什么呀？

生 点。

师 对，只要数一数两点之间的线段有几条，就可以知道平行四边形有几个了，是不是？

第三个也是形式上的拓展，从限定在一条直线上的点的组合问题拓展到没有位置限定的点的组合问题，设置了握手问题和单循环赛问题，引导学生发现依然可以通过数线段条数的方法解决。

三、课后反思

反思这节课的教学过程，除了充分利用表象，使学生经历数学化这一特征，还有一些亮点和不足，由此可以得到一些教学启示。

（一）情境設置要能促进学生的理解

情境教学是新课程改革倡导的教学方式之一。深入课堂可以发现，一些所谓的“情境教学”存在误区：为了体现情境教学而设置情境，设置的情境不仅不能启发学生思考，还容易误导学生。因此，设置情境应该特别关注促进学生理解、帮助学生学习这样的出发点。本节课中的几个情境确实做到了这一点。“鼹鼠钻洞”“菜地旅行”的情境都在无形中将问题限定为在一条直线上取点，让学生更容易找到数线段的规律。

（二）启发式教学不会过时

启发式教学是一个古老的话题，但是不会过时，因为它行之有效。新课改对启发式教学也有强调，如《义务教育数学课程标准（2011年版）》指出：“处理好教师讲授与学生自主学习的关系，注重启发学生积极思考。”本节课的教学很注重启发学生积极思考，所有的规律和结论都是在教师引导下由学生思考或探究得出的，而不是教师告知的。尤其是教师的很多提问都具有启发性。例如，强调数线段条数的顺序时，提问：“我发现同学们在数的时候都没有多数或少数，为什么？你们是怎么做到的？”再如，处理往返车票问题，解释“乘2”的意义时，提问：“你从哪里看出来要乘2？从哪里看出来跟我们刚才的车票问题是不一样的？”这样的提问都很含蓄，指出了思考的方向，留下了思考的空间。

（三）要使不同的人在数学上得到不同的发展

《义务教育数学课程标准（2011年版）》提出了“不同的人在数学上得到不同的发展”的数学教育理念。这一理念不仅要求数学教学尊重学生的主体性地位，而且要求数学教学正视学生的差异，尊重学生的个性，做到因材施教。这节课上，教师对学生的差异关注得不够：给出“鼹鼠钻洞”的情境后，有三名学生不需要借助表象操作，给出了“直接列式计算”的方法，但是，教师始终没有关注这种做法，导致这三名学生在接下来的问题处理过程中，再也没有直接列式计算，而是开始画线段图数线段了。对于这三名学生来说，这种借助表象操作的数学化过程是否是思维的倒退？他们当时是如何思考得出算式的？这些都需要教师的进一步关注。这三名学生有可能就是Lynn Paine教授所说的“原本自己可以学会游泳的孩子”，结果“才能被埋没了”。不过，这节课上，教师将列出算式后涉及的等差数列求和问题留到以后解决（可以留到六年级上册的“比赛场次”教学中解决，并可以延伸到一般的情况），对教材中的组合问题进行了三个拓展（在学生可以接受的范围内，为后续内容的学习做好了铺垫），体现了教学的层次性，是因材施教的有效途径之一。

参考文献：

[1] 弗赖登塔尔.作为教育任务的数学[M].陈昌平， 唐瑞芬，等编译.上海：上海教育出版社，1999.

[2] 张奠宙，宋乃庆.数学教育概论（第三版）[M].北京：高等教育出版社，2016.

[3] 孔凡哲.学会数学化 切实提升数学学科素养[J].小学数学教师，2015（6）.

[4] 彭纲.数学学科核心素养养成的关键是学会数学化[J].小学教学（数学版），2021（6）.

[5] 顾泠沅，王洁.教师在教育行动中成长——以课例为载体的教师教育模式研究（上）[J].课程·教材·教法，2003（1）.

[6] 顾泠沅.课堂视野中的教师及其指导者[J].课程·教材·教法，2014（1）.

[7] 俞宏毓.“长方形和正方形的面积与周长”教学指導研究报告[J].数学教育学报，2014（3）.

[8] 顾泠沅.口述教改——地区实验或研究纪事[M].上海：上海教育出版社，2014.

*本文系2020年度江苏高校哲学社会科学研究一般项目“义务教育阶段课堂教学存在问题及改进研究”（编号：2020SJA0196）和2020年江苏省社科基金后期资助项目“教师发展指导者研究”（编号：20HQ054）的阶段性研究成果。相关研究得到浙江省义乌市绣湖小学朱剑英、李玲静等老师的支持，以及南京信息工程大学人才启动基金的资助，特此致谢。