基于方向图变换的快速不连续相位展开

廖宇铖，伍世虔,4，邓高旭，陈 彬,4

（1.武汉科技大学 信息科学与工程学院，湖北 武汉 430081；2.武汉科技大学 冶金装备及其控制教育部重点实验室，湖北 武汉 430081；3.武汉科技大学 冶金自动化与检测技术教育部工程研究中心，湖北 武汉 430081；4.武汉科技大学 机器人与智能系统研究院，湖北 武汉 430081）

引言

相位展开是从(-π,+π]的包裹相位中获得连续相位的过程，广泛应用于干涉合成孔径雷达、干涉合成孔径声纳、光学干涉和相位测量轮廓术[1-3]。在理想情况下，相邻2 个像素点的包裹相位差不会超过2 π。这时，展开相位可以通过任意路径的积分所获得。事实上，展开相位的正确性始终会受到相位的不连续、噪声和阴影等因素的影响。至今为止，相位展开仍然是一个具有挑战性的问题[4-5]。

相位展开可分为时间相位展开法和空间相位展开法[6-9]。时间相位展开法可以有效地展开具有较大不连续性和孤立区域的包裹相位，但是需要在不同时刻投影多幅不同频率的条纹图案，因此会花费很多时间[10-12]。空间相位展开法根据包裹相位图的一些空间特征和2 π相位跳变等信息就能进行相位展开，其速度快、应用范围广[13-14]。空间相位展开算法大致可分为路径跟踪算法和最小范数法。路径跟踪算法高效且鲁棒，它依赖不同的方法来保证展开路径的可靠性。质量引导算法是路径跟踪算法中具有代表性的一种算法，它根据相位的质量图来引导展开路径，其中几种常见的质量图有：伪相关系数图、相位导数方差图、最大相位梯度图等。由于该方法是通过路径展开相位，一旦1 个像素展开出错，误差则会沿着路径传播，从而导致相位展开失败。最小二乘法是最小范数法中经典的算法，其原理是在全局范围内最小化代价函数，从而获得连续的展开相位[15-17]。Ghiglia等[18]提出了一种最小二乘相位展开算法，并通过快速余弦变换展开相位。Lu 和Wang[19]提出了相位导数方差相关图，该图能够很好地反映包裹相位的质量，并将其作为加权系数带入最小二乘法，得到了平滑的相位。Xia 等[20]提出了相位校准的迭代最小二乘算法，可以抵抗较大的散斑噪声。然而在实际应用中，由于物体的高度或者其他因素，相位会突然变化从而产生相位的不连续。而这些算法在处理不连续相位时总会在不连续的区域上出现错误。

针对不连续的问题，本文提出了快速、简单的算法。该算法利用结构张量计算出每个像素点的方向角，将其映射到三维空间。通过计算找到不连续的区域，并将其作为加权系数带入到最小二乘法来展开相位。实验证明该方法能快速地识别不连续位置，能准确地获得正确的展开相位。

1 相关工作

1.1 加权最小二乘相位展开算法

包裹相位 ψi,j和展开相位 ϕi,j之间的关系为

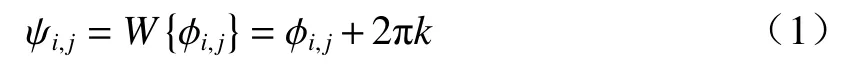
式中：k为整数；W{·}为包裹算子。

相位展开是为了将 ψi,j展开为 ϕi,j，加权最小二乘的原理是在全局范围内使展开相位差值和包裹相位差值的差异最小，即：

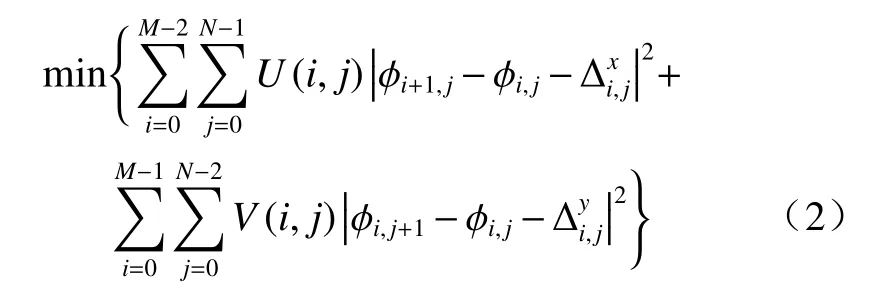
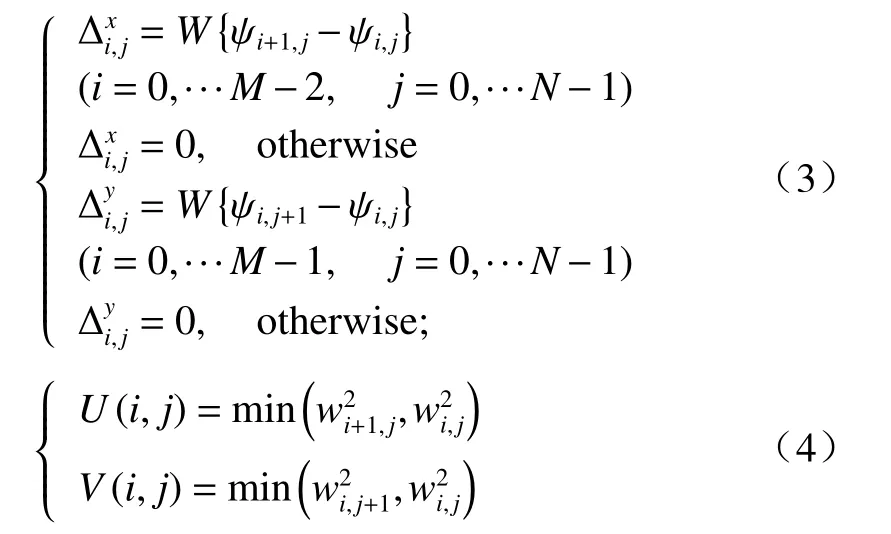
式中：wi,j为二值权重系数，表示该点的可靠度。

对公式（2）求偏导，可以得到如公式（5）所示的离散泊松方程：

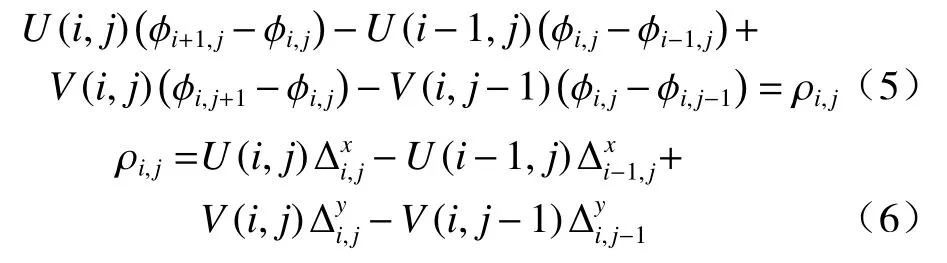
对公式（5）利用预处理共轭梯度算法（preconditioned conjugate gradient，PCG）进行迭代相位展开。对于加权最小二乘法，权重系数图的质量直接决定了相位展开的精度和速度，本文提出了计算权重系数图的新算法。

1.2 基于方向图变换的权重系数图求解

1.2.1 方向图求取

为了减少传感器和其他影响导致的图像缺陷，将图像进行归一化。G(x,y)表示点(x,y)归一化后的灰度值，图像归一化如公式（7）所示：

式中：µ和 σ2分别表示图像f的平均灰度值和方差；µd和分别表示期望的平均值和方差(一般来说，。

图像的梯度 ∇g对边缘检测有很大的作用，但不适合寻找平行结构或者方向。为了拿到包裹相位图的方向，使用公式（8）所示的结构张量进行求解：

式中：∇gσ是经过高斯平滑后的图像梯度。

公式（8）得到2×2 的矩阵，可简化为

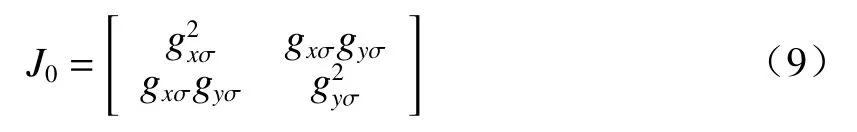
该矩阵为图像的结构张量，通常用来分析和提取图像的局部信息，即局部范围内所表示的方向以及方向的相关程度。为了计算出准确的方向，对结构张量进行增强，如公式（10）所示：

式中：E为图像的能量；G(wk,wl)为傅里叶变换后的图像，其关系如公式（11）所示:

对于增强后的结构张量，计算出特征值 µ1和µ2(µ1≥µ2)。µ1和 µ2反映了图像的局部结构特征，其中特征值 µ2对应的特征向量 ω2表示边缘方向的估计，即相位条纹方向，如公式（12）和公式（13）所示：

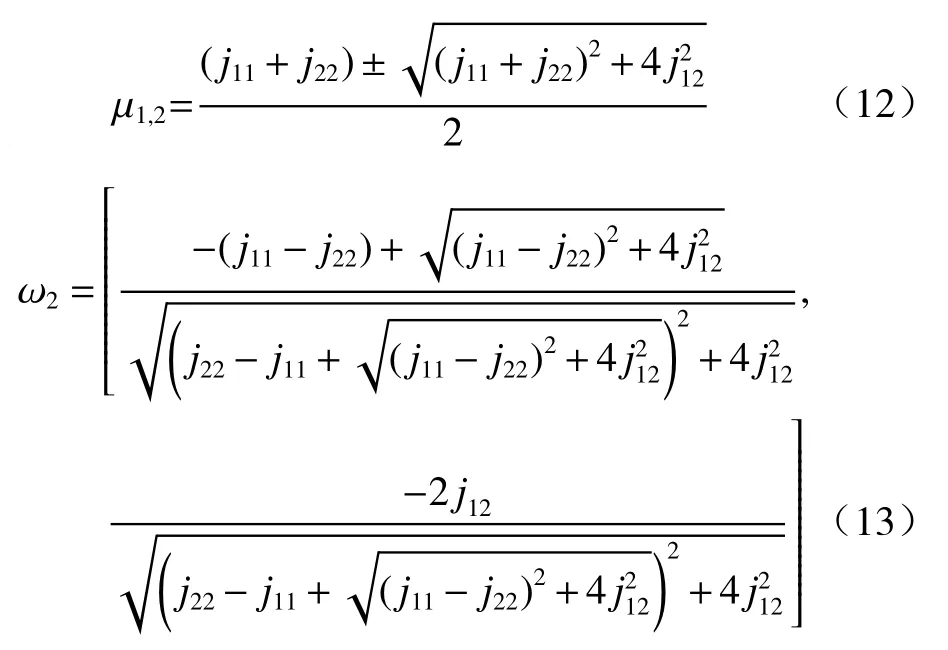
用特征值 µ2对应的特征向量 ω2计算图像中每个点的方向角θ(x,y)，如公式（14）所示：

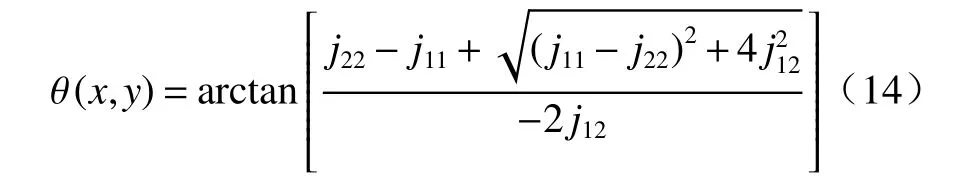
计算出每个点的方向角θ(x,y)，最终获得方向图θ。

1.2.2 不连续位置识别

求出方向角之后，为了找出不连续位置，将方向图θ按行生成一维向量 λ（其中 θi,j变换为 λk），对其中每个元素 λk进行公式（15）所示的变换。然后求出相邻2 点间的距离，如公式（16）所示：

式中：m和n分别表示方向图的行和列。Δfx(λk)对方向的变化很敏感，其值随着方向的变化而变化。求出Δfx(λk)之后，将其还原为矩阵得到Δxθi,j。然后将方向图按列排列成向量，用同样的方法求得Δyθi,j。在对方向图进行变化差分后，将设定一个阈值求得权重图，如公式（17）所示：

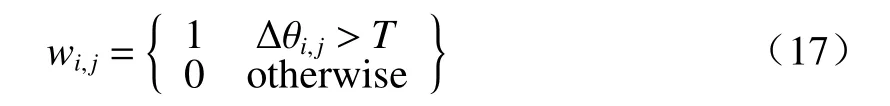
式中：wi,j是图像的权重因子；Δθi,j为与的和。值为1表示可靠度较高的像素，值为0表示可靠度较低的像素。在本文中，T的取值为之间。该权重因子即为包裹相位的权重系数，通过加权最小二乘迭代求得包裹图像的展开解。

2 数值仿真结果

本节利用计算机仿真的条纹图验证所提出算法的有效性，并和其他3 种算法进行对比。分别是相位导数方差相关图（derivative variance correlation map,DVCM）[18]、可靠性图（reliability map,RM）[14]以及相位拉普拉斯导数方差（phase Laplace derivative variance,PLDV）[17]。如图1所示，用计算机生成连续的倾斜相位图像，其函数关系式为

图1 计算机生成的连续相位图Fig.1 Continuous phase diagrams generated by computer

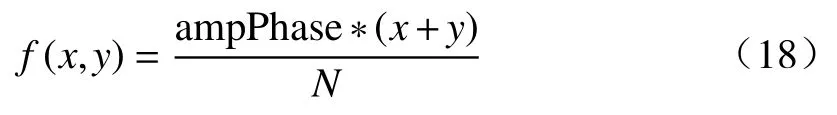
式中：ampPhase为幅度；x和y分别为图像像素的横、纵坐标；N表示图像的大小。在本实验中，N为512，即图像尺寸为512×512。生成连续的相位图后，用MATLAB 的wrapToPi 函数将其包裹。

在本实验中，仿真实验将在无噪声和低噪声环境下进行，然后使用4 个方法分别进行不连续区域的检测。

图2（a1）和图2（b1）分别是无噪声和低噪声条件下的包裹相位，图2（a2）～图2（a5）和图2（b2）～图2（b5）分别对应无噪声和低噪声条件下RM、DVCM、PLDV 和本文所提出的方法检测出的不连续点。

图2 不连续区域的检测Fig.2 Detection of discontinuous areas

从图2 中可以看出，当图像不存在噪声时，4 种算法均能检测出不连续的区域。DVCM 和PLDV 算法检测出的不是一条直线，而是离散的点或者线段。随着噪声的加强，不连续的边缘也会被噪声影响。RM 算法虽然检测到了一条直线，但是其周围出现了一些噪声点（为了方便对比，将噪声点以*标记出来），会影响展开效果，从而导致解包的精度下降。DVCM 和PLDV 算法能检测到的点逐渐稀疏，但大致上还能看出是一条直线。本文提出的方法在无噪声和低噪声条件下，可以准确检测出完整的不连续位置。

为了比较这4 个方法展开图像的质量，本文计算了不连续位置的检测准确度和展开图像的均方误差（RMSE）。对于不连续位置的检测准确度，提出了如公式（19）的平均误差计算方法，用于计算检测出的不连续位置和真实不连续位置的误差。

式中：gi是检测到的不连续点；pi是真实的不连续点；k为检测出不连续点的总数。

RMSE表示计算所得展开图像和真实展开图像之间的差别，如公式（20）所示：

式中：ϕi为计算所得展开相位值；为理论展开相位值。RMSE的值越小，代表展开相位的质量越好。在表1 中可以看到，所提出的方法在展开的相位图上表现最好，在无噪声和低噪声的条件下RMSE都在0.4 以下。

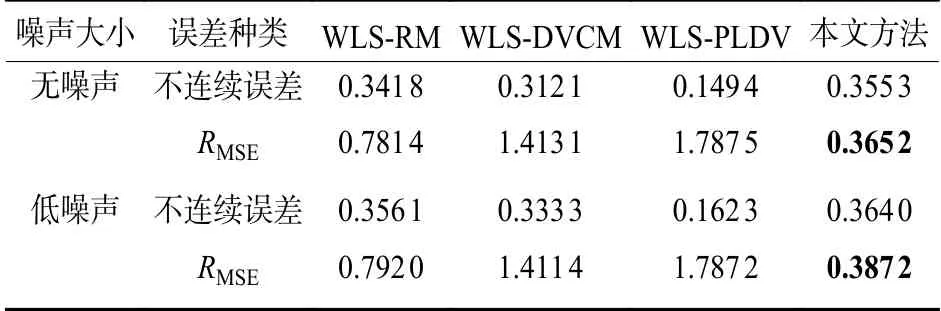
表1 不同方法的测量误差Table 1 Measurement error of different methods

图3（a1）和图3（b1）分别是无噪声和低噪声条件下的展开相位；图3（a2）～图3（a5）和图3（b2）～图3（b5）分别是RM、DVCM、PLDV 和本文所提出的方法在无噪声和低噪声条件下所检测出的不连续点；图3（a6）～图3（a9）和图3（b6）～图3（b9）分别是对应的展开相位。

图3 不同算法的不连续点检测和展开相位图Fig.3 Detection of discontinuous points and unwrapping phase diagrams of different algorithms

无噪声下检测的不连续图和展开效果图如图3（a1）～图3（a9）所示，低噪声下的不连续图和展开效果图如图4（b1）～图4（b9）所示。图3（a3）、图3（a4）分别是WLS-DVCM、WLS-PLDV 计算出的不连续点，如表1所示，其不连续区域的误差比提出的方法要小很多。但是在实际展开的图上，WLS-PLDV 和WLS-DVCM 的矩形区域相位跳变很小，灰度变化不明显。由于最小二乘法旨在最小化目标函数，因此矩形区域线条断开的地方图像的相位会受到影响，导致相位跳变过小，进一步影响周围的点。WLS-RM 和本文提出的方法都检测出了完整的矩形。

图4 是展开相位图在第160 行所取得的相位值。其中黑色的曲线代表原始相位图上的变化趋势，而蓝色的曲线表示本文的方法所展开的相位值，其值和变化趋势都非常接近原始相位。而WLS-PLDV、WLS-DVCM 和WLS-RM 都无法正确地展开包裹相位。

图4 第160 行的展开相位值Fig.4 Unwrapped phase value on line 160

3 实验过程

为了验证提出算法的有效性，使用DLP 投影仪（Acer K137i DLP projector）和NiKON D810 相机组成的结构光对篮球和胶带进行拍照，其装置图如图5所示。

图5 结构光装置Fig.5 Structured light device

用计算机生成分辨率为800×1 280 pixels 的正弦光栅条纹。图6（a）和图6（c）为拍摄到的物体图，图6（b）和图6（d）是计算得到的包裹相位图。

图6 物体的光栅图片和包裹相位图Fig.6 Raster images of objects and wrapped phase diagram

由于篮球和胶带有一定的高度，条纹在投射到平面和物体上时，在篮球的曲面和胶带侧面上将会产生一定的弯曲，这样就会造成相位的不连续。用本文提出的算法对其进行相位展开，其展开效果图如图7（a）和图7（c）所示。图7 中可以看出，篮球所在区域的相位都会发生变化，整体有一个跳变。图7（b）和图7（d）是将其他算法和本算法计算出的展开相位的对比图。

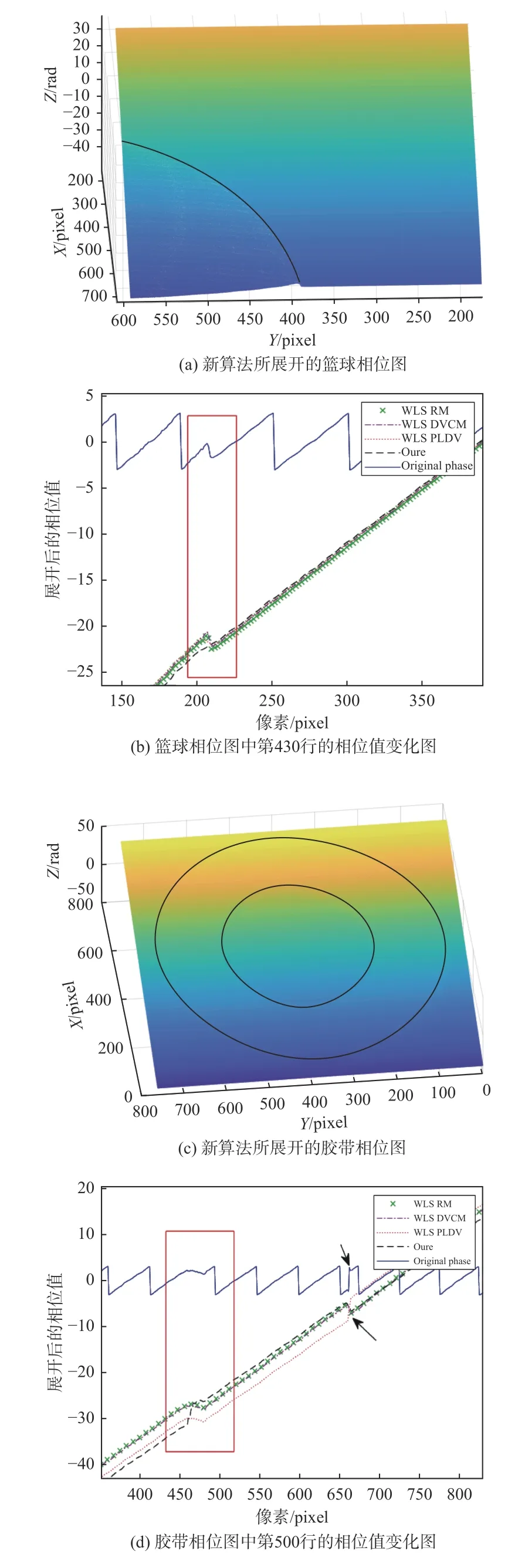
图7 展开相位图的比较Fig.7 Comparison of unwrapping phase diagrams

在图7（b）和图7（d）中，矩形中的区域表示了相位的不连续，在此区域中，相位的变化应和包裹相位有差异。而图7（b）和图7（d）中WLS-RM、WLS-DVCM 和WLS-PLDV 的变化与包裹相位的变化一致，表示没有检测出该地方的不连续。图7（d）中箭头处说明WLS-PLDV 进行了错误的跳变，从图7（d）中可以看出，只有本文算法检测到由胶带表面高度调制对相位所带来的变化。表2 给出了检测出不连续位置所用的时间，可以看出所提算法消耗的时间最短。

表2 计算不连续区域所用的时间Table 2 Time used to calculate discontinuous areas

4 结论

包裹相位图中的相位不连续会导致相位在不连续位置的展开存在较大误差，为了解决这一问题，本文提出了基于方向图变换的快速、简单的加权最小二乘相位展开算法。利用包裹相位图的结构张量信息，精确地检测出不连续的位置，从而提高了相位展开的精确度。计算机仿真实验和实际实验结果表明，本文提出的算法在速度与精确度上都有较好的结果。