基于偏振衍射色散共焦的光学元件轴向间距测量

宁悦文，胡 摇，陶 鑫，郝 群

（北京理工大学 光电学院 精密光电测试仪器及技术北京市重点实验室，北京 100081）

引言

在精密光学系统中，光学元件的轴向精确定位是至关重要的。例如，在微型成像系统、显微物镜、手机镜头等精密测量系统中，光学元件装配的微小偏差都会引起像差，从而降低系统性能[1-3]。因此，对光学元件轴向间距进行高精度、非接触的测量，对减小装配过程中的误差，改善光学系统的成像性能具有重要意义。

在早期的光学元件间距测量中，常采用接触测高仪[4]的方法，在测量中容易损害光学元件表面，并且难以准确确定被测镜头顶点的位置，测量精度有限。相比之下，非接触式的光电测量方法有效避免了上述问题，例如低相干光干涉法[5-7]、激光差动共焦法[8]、色散共焦法[9-11]等。然而，低相干光干涉法和激光差动共焦法在测量中都需进行轴向扫描，测量实时性差。

色散共焦法利用色散物镜产生轴向色差，通过分析被测物表面反射回的光谱信号，得到被测物的位置信息，具有高精度、高实时性的优势。可以应用于透明物体厚度测量[12-13]，如文献[13]对厚度为11 mm 的k9 玻璃平板进行厚度测量，测量精度为1 μm。受到色散物镜色散能力的限制，色散共焦系统测量范围小，主要应用于小型及轻薄光学元件的厚度测量，难以满足光学元件轴向间距测量范围要求。在色散共焦测量系统中，色散物镜是决定系统性能的关键元件，用于实现对波长、位移的编码。现有色散物镜多采用折射式，色散范围多为微米量级[14-15]。文献[16]的色散物镜采用多片镜头增大色散范围，在400 nm～1 000 nm波段，色散范围可以达到30 mm，但结构复杂，装调难度高。因此，折射式色散物镜难以满足测量范围为厘米量级的光学元件轴向间距测量要求。

衍射式色散物镜则在获得大色差上具有明显优势，根据菲涅尔衍射原理，单片衍射镜头便可以获得厘米量级的色差。由于衍射元件加工工艺有限带来的衍射效率低、多衍射级次混叠导致无法得到准确有效的测量信号，是目前需要解决的一大难题。

针对上述问题，本文采用偏振衍射色散物镜作为色散物镜，结合衍射和几何相位原理，在510 nm～620 nm 波段，能够实现25 mm 的轴向色差。由于其特殊的偏振特性，当入射光为特定圆偏光时，1级衍射效率超过90%，有效地解决了衍射镜头造成的多个衍射级次混叠的问题，其单片镜头的结构也降低了系统装调的复杂度，满足了系统的测量要求。

1 测量原理和系统实现

1.1 偏振衍射色散物镜特性

偏振衍射色散物镜利用衍射原理实现负色散，其色差主要取决于色散物镜的结构参数。复色光经偏振衍射色散物镜调制后，不同波长的光聚焦于光轴不同的位置。根据光栅衍射原理，当波长为λ时，推导对应焦距f的计算公式如下

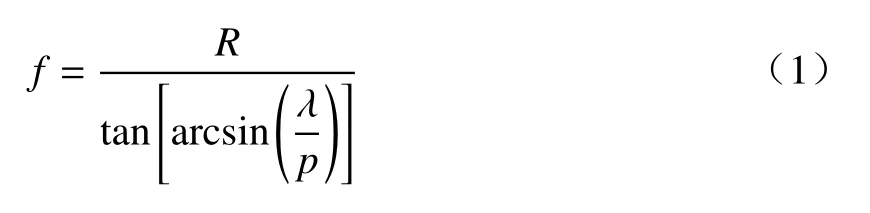
式中：p为周期；R为半口径。当系统的工作波段为λ1～λn时，根据（1）式，偏振衍射色散物镜的轴向色差Δf为

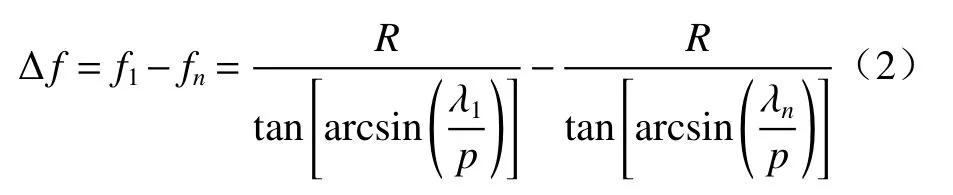
式中：λ1、λn为最短波长和最长波长；f1、fn分别为λ1、λn对应的焦距。由此，只要确定系统的工作波段和偏振衍射色散物镜的结构参数，便可以确定偏振衍射色散物镜的轴向色差，从而确定系统的理论测量范围。

为了提高衍射效率，本文采用的偏振衍射色散物镜结合几何相位原理[17]，利用晶体的双折射特性极大地提高了衍射元件的衍射效率。如图1所示，对于任意偏振态的入射光，经过偏振衍射色散物镜后，出射光仅有±1 级偏振态正交的圆偏光和零级衍射光，其中，+1 级的衍射光会聚，–1 级衍射光发散，±1 级的衍射效率由入射光的偏振态决定。理想情况下，若入射光为特定偏振态的圆偏光，则出射光为+1 级的会聚光，衍射效率接近100%。不过，经偏振衍射色散物镜后，入射光的偏振态变为与入射光正交的圆偏光，因此需在偏振衍射色散物镜后加入λ/4 波片，使被测物反射的光能够以原入射偏振态返回。利用这一特性，只要控制入射光的偏振态，便可只保留+1 级的会聚光，将衍射元件作为具有大色差的光学元件使用。

图1 偏振衍射色散物镜的偏振特性Fig.1 Polarization characteristics of dispersive objectives based on polarization diffraction

1.2 间距测量原理

基于偏振衍射色散物镜的系统测量原理图如图2（a）所示。光源发出的复色光经消色差透镜1 聚焦于共焦小孔1，当小孔足够小时，从共焦小孔1 出射的光可近似看作点光源。点光源经消色差透镜2 准直为平行光，透过分光棱镜，经偏振衍射色散物镜色散后，不同波长的光聚焦于光轴不同的点上，只有刚好聚焦于介质分界面上的光被反射进入光谱仪，得到的光谱峰值波长对应于介质分界面的位置。

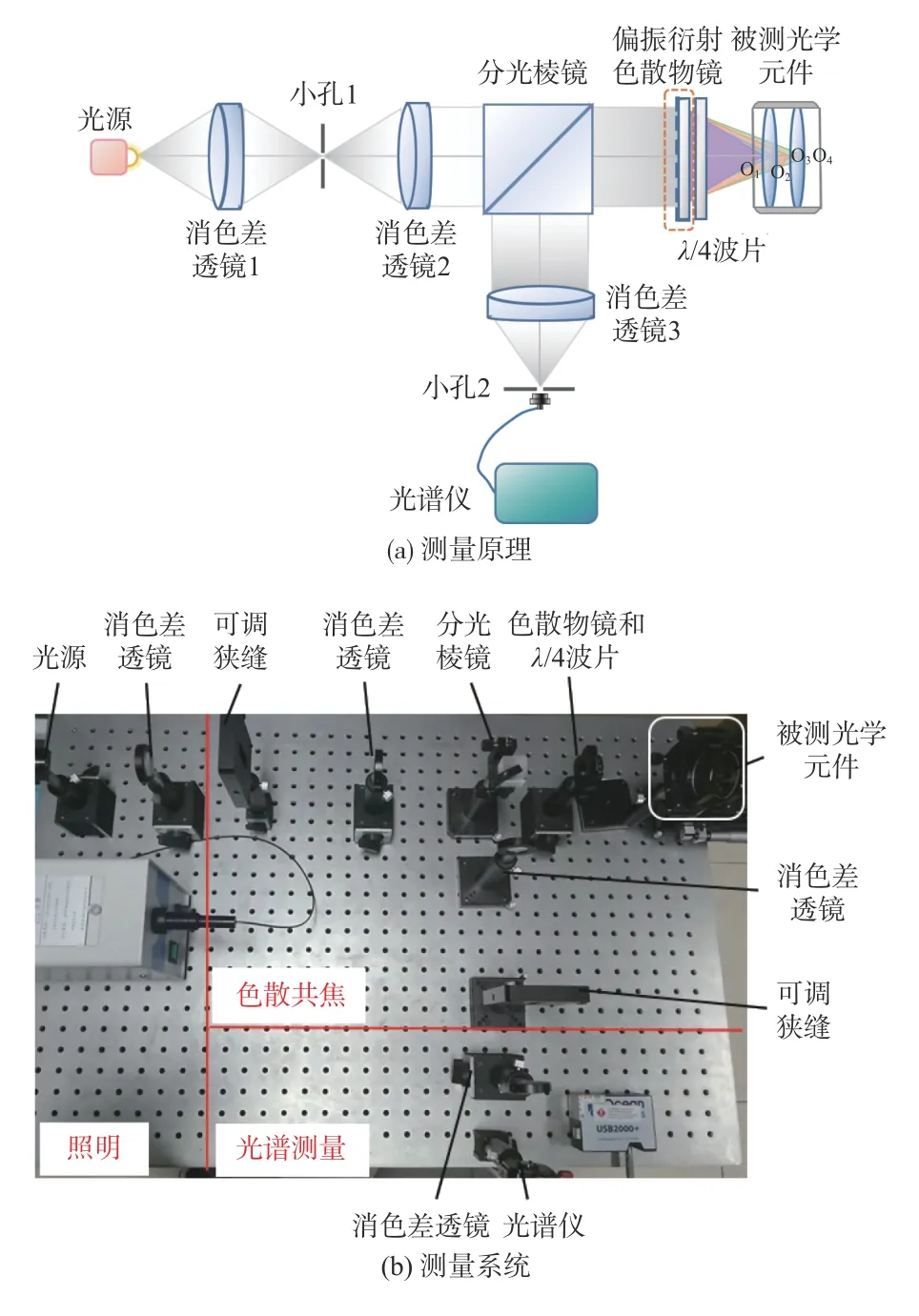
图2 基于偏振色散共焦系统的间距测量原理和系统图Fig.2 Spacing measurement schematic and system diagram based on polarization dispersion confocal system

以透镜间距测量为例，当被测元件置于系统测量范围内时，只有刚好聚焦于被测透镜表面顶点O1、O2、O3、O4的光，经被测透镜反射后被光谱仪接收得到4 个光谱峰值，求解被测元件各表面顶点对应的峰值波长，通过波长位置对应关系，求解不同波长对应的位置。最后根据被测元件的折射率等参数值，利用光线追迹法计算被测元件各表面的位置。

根据上述测量原理，构建实验系统如图2（b）所示，主要由照明部分、色散共焦部分及光谱测量部分组成。光源选用大恒光电GCI-060 101 直流调压光纤光源，光纤内芯直径为1 mm，光源灯泡为150 W 的石英卤素灯。实验中选择光源光强较强的510 nm～620 nm 波段为系统工作波段以提高信噪比。偏振衍射色散物镜为麓邦光电定制，具体参数如下：中心波长为550 nm 时，数值孔径为0.043，焦距为167.885 mm，根据（1）～（2）式可得，在系统工作波段内，偏振衍射色散物镜的轴向色差为32 mm，系统的测量范围理论上可达32 mm。实验所用光谱仪为海洋光学光纤光谱仪USB 2 000，测量范围为349 nm～1 027 nm，分辨率为0.379 nm。

1.3 波长-位置标定方法

实际测量中，需先对系统进行标定，求解波长与位置的对应关系。将图2 中被测光学元件替换为平面反射镜进行系统标定。以偏振衍射色散物镜标称中心波长焦距为参考，选取λ/4 波片后距离不超出该焦距的点为原点，向远离测量系统端移动平面反射镜，精确测量反射镜的轴向位置，获取不同位置对应的光谱峰值波长，即可获得不同位置与波长的对应关系。其中，最短波长与最长波长对应的位移为系统的测量范围。

2 厚度及间距测量实验

透镜厚度和轴向间距测量实验的样品为2 片大恒光电GCL-010835 平凸透镜，材料均为JGS1，折射率为1.46，被测面的曲率半径依次为368.06 mm、∞、368.06 mm、∞，使用千分尺测得厚度分别为5.050 mm、5.040 mm。

如图3所示，测量时，先将平凸透镜1 和平凸透镜2 无间隙固定，并利用激光束准直原理调节被测透镜与系统光路共轴。只将平凸透镜2 固定在平移台上，调节平移台，移动d2= 15.000 mm 的位移，此时，认为平凸透镜1 和平凸透镜2 的间距为15.000 mm，得到被测光谱信号如图4（a）所示。峰值波长从右到左依次对应平凸透镜1 的前后表面、平凸透镜2 的前后表面。根据1.2 节所述原理计算被测透镜间距和厚度，平凸透镜1 的厚度d1=5.048 mm，间距d2=15.008 mm，平凸透镜2 的厚度d3=5.030 mm。

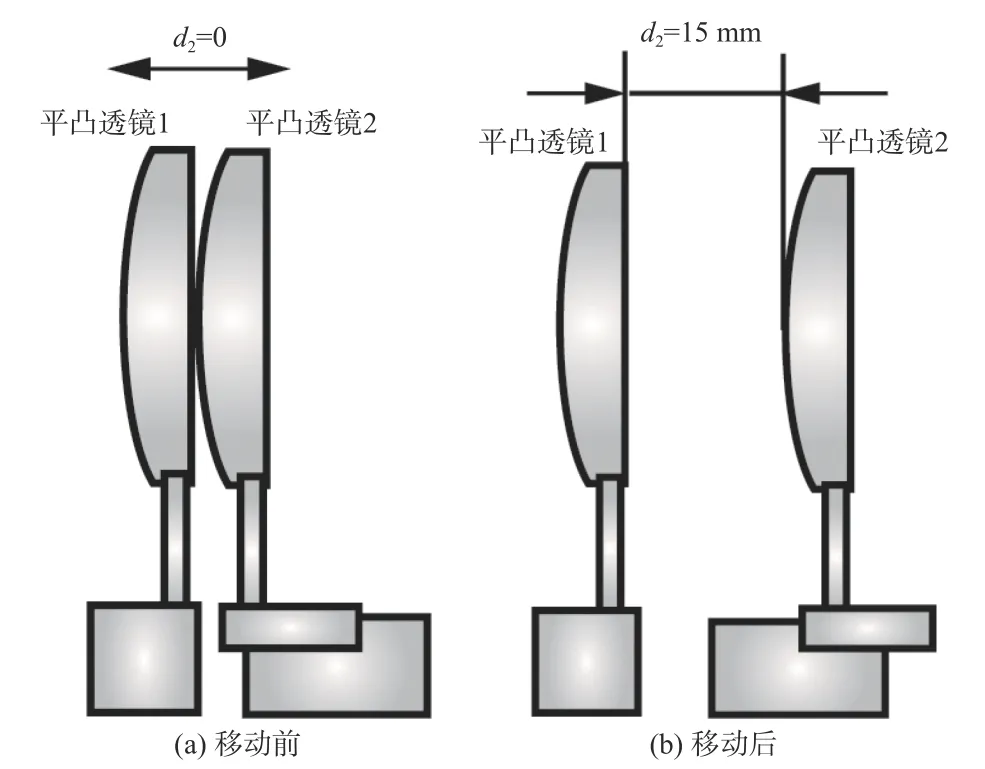
图3 平凸透镜间距测量示意图Fig.3 Schematic diagram of planoconvex lenses spacing measurement

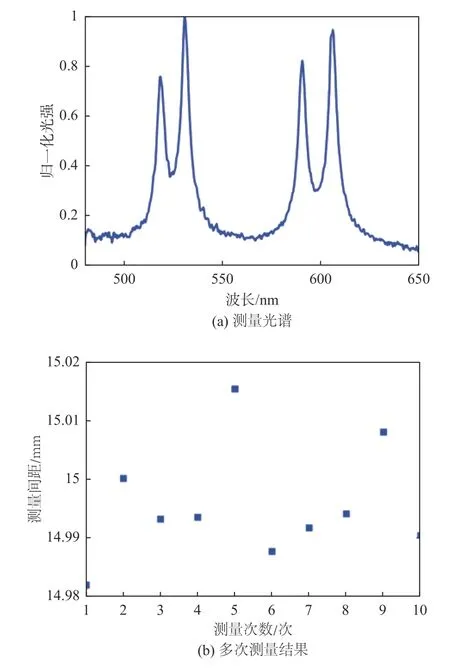
图4 测量光谱及测量结果Fig.4 Measuring spectrum and results

移动平移台，多次调节透镜间距为15.000 mm，对被测透镜间距进行10 次重复测量，多次测量结果如图4（b）所示。间距测量的平均值为14.996 mm，标准差为10 μm，相对标准差为6.7×10-4。

3 结论

本文提出一种基于色散共焦测量原理的光学元件轴向间距测量方法，该方法利用单片偏振衍射光学元件获得大的轴向色差，极大地简化了系统结构，解决了色散共焦测量系统受色散物镜限制测量范围小的问题。对系统进行标定，并对2 个平凸透镜的厚度和轴向间距进行测量，实验结果表明，间距测量精度为10 μm。对实验结果进行分析，证明了该方法的可行性和有效性，为光学系统中光学元件的轴向定位提供了思路，对光学系统辅助装调具有一定意义。