蚁群禁忌搜索融合算法求解调度问题
2021-09-23刘博省毛范海
刘博省,毛范海,钱 峰
(大连理工大学机械工程学院,辽宁 大连116024)
1 引言
车间调度是一个历史悠久的优化问题,其本质是通过资源的分配和时间的先后顺序来完成不同的生产任务,使预定目标最优化。随着汽车行业的发展,其部件的装配生产线越来越多的面对着多品种、小批量和个性化的制造需求[1]。一方面,传统的凭借经验或简单的确定性规则的排产算法(大多数企业当前的排产方法)难以得到使预订目标最优化的调度;另一方面,动态规划、分枝定界等优化方法可以得到理论上的最优解,但由于算力的制约无法解决大规模的调度问题。所以研究者们将一系列元启发式算法应用在车间调度问题上,取得了一些成果。
文献[2]针对作业车间调度问题,提出了一种并行模拟退火算法,在小规模Job-shop问题上取得了较好的效果;文献[3]提出了一种改进遗传算法来解决JSP问题,运用多种策略丰富解的空间,获得了较好的解;文献[4]针对采用粒子群优化算法解决流水车间调度问题进行了研究综述;文献[5]采用粒子群算法来解JSP问题,用MK01-MK10等十个问题验证了解的有效性。
为解决发动机缸体混流生产线的生产调度问题,将其抽象为Job-shop问题后提出一种基于蚁群和禁忌搜索的混合算法,并进行实例仿真得出此方法的有效性和性能。
2 JSP问题描述及其数学模型建立
2.1 Job-shop问题的描述
n个工件在m台机器上加工,工件均包含m个工序,要求最大完工时间最小(Makespan:最大完工时间,JSP中最常用的研究指标)。Job-shop问题的基本约束条件如下:
(1)各工件服从工艺路线约束;
(2)各工序必须在指定机器上加工;
(3)同一时刻一台机器只能加工一个工序;
(4)必须等到前一道工序加工完毕后一个工序才能开始加工;
(5)每个工序在可用机器上的加工时间确定;
(6)允许工件和机器存在等待时间;
(7)工序一旦开始则不允许中断;
Job-shop问题的求解也即为得到一个满足上述约束条件的可行解,从而优化特定的生产性能指标。
2.2 Job-shop的数学模型
Job-shop是许多实混流装配线的简化模型,也是目前研究非常广泛的生产调度问题的简化模型,其数学模型可表示为下:

式中:cik—i工件在机器k上的完成时间,pih—i工件在机器h上的加工时间,aihk—指示系数,其意义为:

式中:xihk—知识变量,其意义为:

式(2)表示工序约束,即工件的后一个工序要在前一个工序的加工完成的基础上才能开始加工;式(3)表示资源约束,即同一台机器上不能有两项工序同时加工;式(4)表示每个工件的每个工序的加工时间都为正数;M是一个足够大的正数。文献[6]问题求解是一个典型的NP-hard问题,至今没有找到可以精确求得最优解的多项式算法。
3 融合算法原理与步骤
3.1 蚁群算法原理
蚁群算法由文献[7]首先提出并应用于Job-shop问题,蚁群算法在Job-shop问题应用方式如下:使用蚁群算法求解Job-shop问题时,蚂蚁从0结点出发,遍历每一个结点直至10结点,得到的工序序列即为问题的一个解。蚂蚁爬行时结点选择由状态转移规则确定;每只蚂蚁爬行过程中进行信息素更新,由信息素更新公式确定。
故本研究采用状态转移规则和信息素更新方法有所改进的蚁群系统(Ant Colony System)进行求解。
(1)改进的状态转移规则

式中:Sk—序号为k的蚂蚁所选择的下一个工序;q—一个生成的随机数;q0—阈值,若蚂蚁选择结点时的随机数q≤q0,则按照第一种情况选择下一个结点,即所选结点使得整个表达式的值最大,这被称为对知识的“利用”;反之,若q≥q0,则按照以下公式计算待选工序各自的概率,然后按照“轮盘赌”方法做出选择,这被称为“探索”。
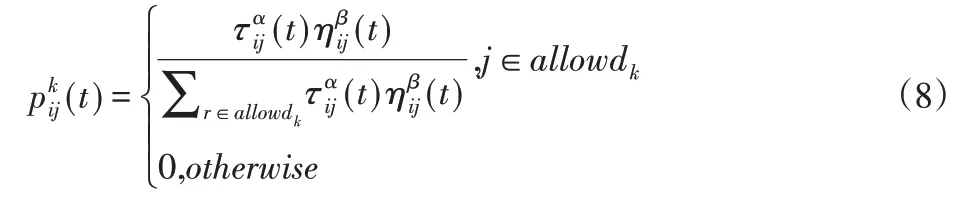
(2)改进的信息素更新方法
基本蚁群算法在一次迭代中所有蚂蚁爬行完成后进行信息素的更新,更新公式如下:

式中:蒸发因子ρ∈(0,1),Δτij—所有蚂蚁信息素增量之和,在本算法中采用蚁周模型(Ant-Quantity System),计算方法如下:

蚁群系统在在基本蚁群算法信息素更新的基础上增加了“信息素局部更新机制”,在蚂蚁爬行结束时即更新信息素,用来扩大搜索范围,公式如下:

式中:局部蒸发因子ρ0∈(0,1),当蚂蚁爬行完成后,其走过的工序路径的信息素以ρ0的速率蒸发,使得之后的蚂蚁重复选择路径的概率较小。
3.2 禁忌搜索算法原理
禁忌搜索(Tabu Search,TS)的思想最先由文献[8]于1986年提出,是对局部搜索算法的一种改进。该算法的基本原理是:对某问题给定一个初始解和领域结构,在领域中通过一定规则确定若干候选解;若这些候选解的值的值好于当前的最优解,则藐视准则被触发,忽视禁忌状态,用其替代当前解和最佳状态,并纳入禁忌表;若候选解均不好于最优解,则从候选解中找出最优,将其加入禁忌表中;如此不断迭代上述过程,直至满足停止准则。
禁忌搜索算法的核心问题有以下几个:
(1)解的编码
为了和蚁群算法更好的融合,禁忌搜索沿用了蚁群算法的编码方式,即用自然数给工序排序,得到的自然数序列即为编码。
(2)邻域结构
采用互换操作随机选择编码中不同的两个基因进行交换。为保证交换后总能得到可行解,通过算法设计使得交换结果保证“属于同一工件的不同工序不能发生变化”。
(3)终止准则
为保证算法的搜索范围,采用连续m代最优解相同的终止准则。
3.3 融合原理与步骤
经过对上述两种算法的原理与结构分析可知,这两种算法具有以下共同性:
(1)概率型全局优化算法
交叉、状态转移、“轮盘赌”选择等本质上都是基于概率的选取[9],有利于在全局范围内搜寻最优解。
(2)同为仿生元启发式算法
蚁群算法和禁忌搜索均为基于仿生优化的元启发式算法,适合大规模计算。
同时蚁群算法和禁忌搜索又具有各自的特点:
(1)蚁群算法特点
蚁群算法是基于生物群体启发行为的随机搜索优化方法,具有很强的解搜索能力和鲁棒性[10]。正反馈特性能够加快算法的进化速度,使其快速收敛;但蚁群算法也由于其正反馈特点容易陷入早熟陷阱,局部寻优能力有待提高。
(2)禁忌搜索算法特点
禁忌搜索采用禁忌方法,避免了算法选入局部最优,具有很强的局部搜索能力,但对初始解性能有很强的依赖,差的解会降低其收敛速度,甚至造成在有限时间内得不到可接受的解。
基于两种算法的共同性和能够产生互补增益的特点,进行蚁群禁忌搜索算法的融合来解决Job-shop问题,融合算法流程,如图1所示。

图1 融合算法流程图Fig1.Fusion Algorithm Flow Chart
4 仿真与评价
4.1 基准实例仿真
为了验证融合算法的性能,选取LA5作为基准实例进行仿真,该问题为10(工件)×5(机器)的经典Job-shop问题,经过融合算法得到最优调度序列,如图2所示。

图2 LA5调度结果甘特图Fig2.Gantt Chart for Schedule of LA5
从图上可看出最大完工时间(Makespan)为593,这也是LA5问题已知的最优解,证明了融合算法的可行性与有效性。
4.2 算法性能评价
将融合算法应用于Job-shop问题的5个基准实例,并与传统算法得到的结果进行对比,如表1所示。
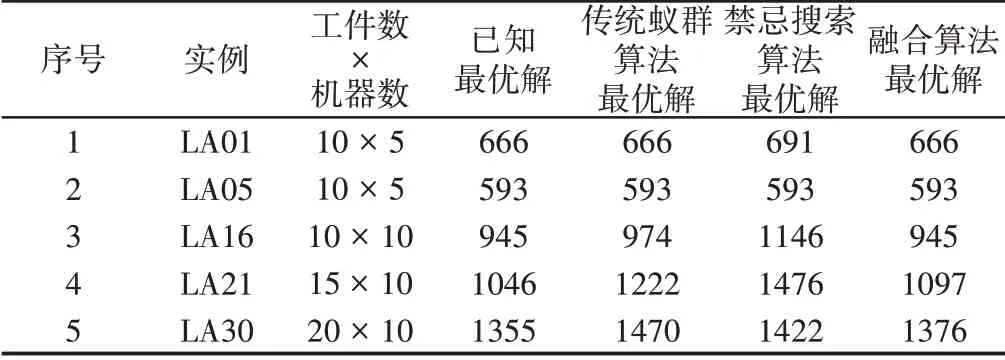
表1 算法结果对比Tab.1 Algorithms’Best Solution Comparison
可以看出,融合算法比传统算法结果更要接近最优解,特别是在求解LA21、LA30等大型问题时,能够得到更好的结果。
4.3 生产试验
以营口HR公司的发动机混流装配线上进行生产实验,装配关键工艺序列为“活塞环、活塞销、后油封、油壳底、飞轮及离合器、凸轮轴、缸盖螺栓、气缸罩盖、进气管、正时系统”。以公司现有的同一平台的7种不同产品为对象,运用蚁群禁忌搜索融合算法进行了生产调度,得到调度甘特图,如图3所示。

图3 混流装配线调度结果Fig3.Schedule of Mixed Assembly Line
调度得到的最大完工时间为773s,这一数据较现场现阶段使用的传统调度方案842s缩短了8.19%的装配周期,证明了算法在实际生产调度中的有效性。
5 结束语
针对汽车发动机混流装配线的调度问题进行研究,对问题进行了抽象和数学建模,应用蚁群禁忌搜索融合算法对模型进行求解,验证了算法的有效性;同时基于基准实例仿真和生产试验验证了融合算法相对传统算法的优越性,对于提升发动机缸体混流装配生产线的效率有一定的实际意义。在已提出的融合算法基础之上,元启发式融合算法仍然有着广阔的研究空间,例如蚁群算法部分的自适应信息素更新、禁忌搜索领域结构的优化等。
