表面结构互动减阻机理数值模拟

2021-09-23焦有威袁卫锋

机械设计与制造 2021年9期

焦有威，袁卫锋，古斌

（西南科技大学制造过程测试技术教育部重点实验室，四川绵阳621010）

1 引言

摩擦引起的能量损耗很大，减小摩擦阻力和磨损是摩擦研究工作的主要内容。为了节能提效，在生活、工程应用中减小摩擦力的主要方式有润滑、材料表面处理或者改变摩擦运动形式，变滑动为滚动等［1］。表面织构对摩擦特性的影响也得到了大量的研究，仿生表面结构可以减小摩擦接触面积［2］，表面织构有储存润滑剂或磨屑，改善摩擦特性，减阻减磨的作用［3］。大多研究只关注了对摩副中一个接触面的结构对摩擦特性的影响，通常另一接触面使用平面、球面或探针［4］。摩擦的主要来源是接触区域咬合产生的阻力［5］，因此普遍认为滑动摩擦副上的双表面结构设计对摩擦减阻没有益处，然而在纳米尺度上M.Hirano从理论上预测晶面在晶格常数和取向不匹配接触时的摩擦力可能为零［6］，紧接着J.Frenken用片状石墨材料实验证实了摩擦力很小的存在［7］。纳米尺度与实际应用尺度相差悬殊，晶面的完整受尺寸的限制，在大尺度下很难实现超摩擦［8］，更大尺度上的摩擦副互动表面结构的研究还没有取得突破性进展。

在干滑动摩擦条件下，固体表面间的摩擦和磨损主要由微观下真实接触区域的咬合和黏着产生。当发生相对滑动时，材料表层发生弹塑性变形，摩擦力做功，消耗能量。为了减小摩擦力做功引起的能量损耗，改变摩擦形式由滚动替代滑动是有效的措施。应用广泛的轴承，将对摩材料之间的滑动摩擦问题转移到了精密配合的轴承内部，减小摩擦力，延长轴的使用寿命［9］。轴承是独立于运动系统的，比较而言产生滚动效果的互动式摩擦副表面结构有以下特点：没有增加额外的零件，表面结构是对摩擦副表面的修饰加工；表面结构互动式的滑动摩擦过程与蜈蚣、百足虫等动物爬行运动方式相似，可以在很低的摩擦阻力下滑动，但对摩擦副表面结构有特定的要求，不匹配的表面结构无法低阻滑动。设计互动式的表面结构滑动摩擦副，通过有限元数值模拟验证，该方法可以在很大程度上减小滑动摩擦力。

2 互动减阻机理

2.1 摩擦互动表面结构介绍

摩擦副表面结构之间的互动效果可以有类似于滚动摩擦替代滑动摩擦的效果。如图1所示，摩擦副由固定表面和滑动表面组成，固定表面上的足结构能在一定弧度内摆动，足结构需要满足三个要求：1、在自由状态下与表面垂直，垂直方向的强度可以承受滑动物体的重力；2、足结构的摆动依赖于其与固定表面连接处发生弯曲变形，其它部分尽量不发生变形；3、足顶弧面曲率半径可以随转动角度变化。滑动表面结构为周期变化的S型曲线，仅有凸棱与足结构接触，凹槽的作用是使接触界面脱离，让足结构有摆动回到原始垂直位置的空间。

图1 表面结构示意图Fig.1 Surface Structure Diagram

2.2 互动减阻机理分析

滑动摩擦副表面结构互动的运动过程如图2所示。（1）处于垂直位置的足结构与滑动表面上的凸棱接触时，足结构承担物体的重力；（2）牵引力作用下滑动表面向右运动，与凸棱保持接触的足结构向右转动；（3）达到最大转动角度后足结构脱离与滑动表面上凸棱的接触状态，没有接触约束的足结构凭借与固定表面连接处的转矩回到垂直位置，等待与滑动表面的下一个凸棱接触。固定表面上的足结构在往复摆动时，与滑动表面上的凸棱发生接触-转动-分离的循环动作，在接触区域没有发生相对滑动，凭借互动的摩擦副表面结构实现局部的滚动摩擦效果。总体上，摩擦力的作用机理发生了改变，可以控制足结构摆动的角度和抗弯刚度来调整转矩的大小，改变滑动物体所受到的摩擦力。足结构的摆动角度与其高度，足顶弧面和凸棱弧面的曲率等参数有关，只有精确的结构尺寸设计才能使滑动物体在固定表面上低阻运动。

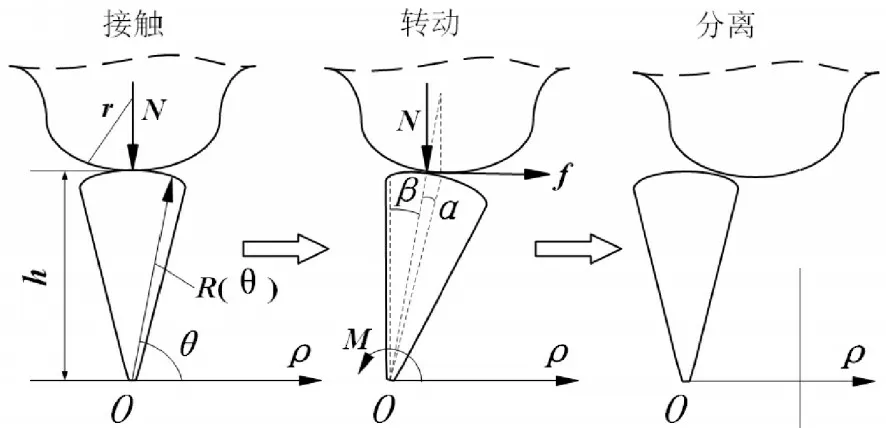
图2 滑动过程分解Fig.2 Sliding Process Decomposition

2.3 受力分析

足结构与凸棱接触时的受力分析如图2所示，足顶弧面受到垂向力N和摩擦力f作用。足顶弧面的曲率随角度θ变化，弧面与凸棱的接触点到足结构转动中心O的距离为R（θ），且R（π/2）=h，凸棱弧面的曲率半径为r。假定足结构抗弯刚度为k，则互动减阻结构的摩擦力可以用公式（1）计算：

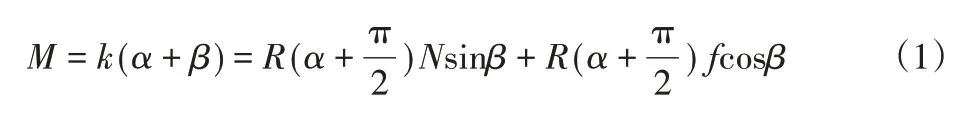
式中M是转矩，足结构的转动角度（α+β）与抗弯刚度k的乘积等于足结构转动后摩擦力f和垂向力N对转动中心O的转矩和，R（α+π/2）是足结构转动后与凸棱的接触点到转动中心O的距离。假设足结构在凸棱上的接触点的弧长位移为w，w/r=β为接触点在凸棱的弧面上转过的角度，也是接触点和转动中心O的连线与垂直位置的夹角，由R（θ）计算得到接触点在足顶弧面上的转动角度为α。摩擦力的大小与足结构的抗弯刚度，转动角度，结构的尺寸和垂向压力等参数有关。抗弯刚度k=2EI/h，当足结构与固定表面连接处为矩形截面时，矩形梁截面的惯性矩I与截面宽度的三次方成正比。

优化互动结构，将足顶弧面半径设置为常值，并且选择足结构的转动中心作为其圆心；让凸棱弧面的曲率半径无穷大时，转动角度β为0，需要将凸棱顶端弧面变成平面。此时公式精简为

滑动表面所受到的摩擦力仅与足结构的抗弯刚度，高度和转动角度有关，而且足顶弧面与凸棱顶端平面的接触点始终在转动中心即足顶弧面圆心的正上方，滑动表面在垂直方向上的位移为0，滑动摩擦过程变得更平稳。

3 摩擦副互动表面结构建模

3.1 二维摩擦结构模型

设计互动表面结构参数如图3所示，固定表面上的足结构高度h=12，足结构顶端弧面宽度d=5，滑动表面的S型曲线结构周期长度l=2.5，为足结构弧面宽度的一半，高度hs=1.2，让凸棱和足结构有平稳的接触状态，将凸棱的弧顶变成一段平面，宽度w=0.6。结构参数确定后，可以计算出足结构摆动角度。建立二维有限元模型，用梁结构模型仿真滑动摩擦过程。在ABAQUS软件中直接绘制模型，如图4所示。

图3 表面结构尺寸设计Fig.3 Surface Structure Size Design

图4 有限元模型Fig.4 Finite Element Model

3.2 材料参数与摩擦接触模型

足结构需要有较强的支撑刚度和往复摆动的灵活性，对材料属性的要求是高弹性模量和较小的密度；对滑动表面结构的要求是尽量不发生变形，在结构互动接触的过程中，除了转动中心以外的结构变形会造成较大的运动阻力。材料参数设置，如表1所示。

表1 材料参数Tab.1 Material Parameters

滑动表面与初始接触平面及足顶弧面的接触方式设置为面-面接触，考虑到滑动结构的材料弹性模量较大，将滑动结构表面定义为主面，其它面为从面。

3.3 载荷及边界条件

对建立好的梁结构互动摩擦模型进行载荷及边界条件的设置：（1）固定足结构底部，并用interation中的springs设置扭矩弹簧，弹簧刚度为k，足结构在自由状态下与表面保持垂直；（2）滑块在平面上开始运动，然后与足结构碰撞接触，在固定表面结构上滑动，滑块表面与初始接触平面的摩擦系数设置为0.1，滑块表面与足顶弧面的摩擦系数设置为0.5；（3）对滑动结构施加重力G和水平方向的拉力F，根据F-f=ma来计算滑动结构表面在固定结构表面上所受到的平均摩擦力；（4）滑动摩擦动态力学分析，采用动力隐示分析，通过滑动结构的水平速度来计算其在足结构表面上滑动的平均加速度。

4 滑动摩擦力分析

改变滑动物体的质量，固定表面受到的法向压力FN=G，摩擦力随法向压力的变化曲线如图5所示，与Amontons摩擦定律计算得到的摩擦力比较，滑动表面在足结构表面上滑动所受到的摩擦力很小，且摩擦力与法向压力无关，打破了摩擦力随载荷增加而增加的定律，在法向压力为90N时的摩擦系数可以减小到0.03。

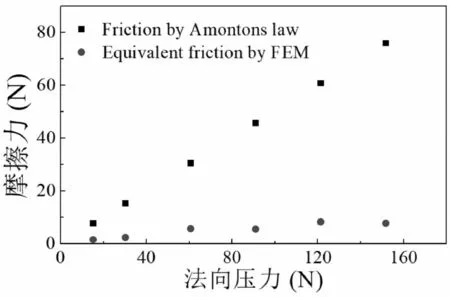
图5 摩擦力与法向压力的关系Fig.5 The Varies of Friction with Normal Load

当足结构往复摆动时，滑动表面所受到的摩擦力与接触面上定义的摩擦系数无关，根据公式（2），与足结构的转动角度，抗弯刚度和高度有关。滑动表面结构与足结构之间的碰撞接触是动态过程，运动过程中，足结构随着凸棱平面发生转动，接触分离后，足结构弯曲累积的弹性能释放，引起振动并随着能量衰减回到原始位置，当足结构再次与凸棱结构碰撞接触时：足顶弧面的转动线速度大于滑动表面的运动速度时，部分能量会回馈给滑动物体；否则，可能成为阻碍物体滑动的力。因此滑动物体在足结构表面上运动时所受到的摩擦力有微小的波动变化。